Lagarul axial hidrostatic
Relatia
(11.69) se rezolva exact si pentru o miscare pur radiala
generata de un gradient de presiune ![]() (v. figura 11.10). In
acest caz, distanta dintre cele doua discuri aflate in miscare
relativa de rotatie este constanta, h = constant, h << R, presiunea
(v. figura 11.10). In
acest caz, distanta dintre cele doua discuri aflate in miscare
relativa de rotatie este constanta, h = constant, h << R, presiunea ![]() fiind introdusa
din exterior. Se creeaza astfel o forta de presiune
portanta care mentine greutatea exercitata pe discul superior
aflat in rotatie cu viteza
fiind introdusa
din exterior. Se creeaza astfel o forta de presiune
portanta care mentine greutatea exercitata pe discul superior
aflat in rotatie cu viteza ![]() la distanta h de placa inferioara,
considerata fixa. Acest tip de miscare sta la baza
constructiei lagarului axial hidrostatic.
la distanta h de placa inferioara,
considerata fixa. Acest tip de miscare sta la baza
constructiei lagarului axial hidrostatic.
Ecuatia (11.69) devine
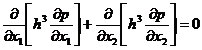 , (11.77)
, (11.77)
iar in coordonate cilindrice cu
![]() (11.78)
(11.78)
se obtine
![]() . (11.79)
. (11.79)
Conditiile la limita sunt
![]() , (11.80)
, (11.80)
![]() . (11.81)
. (11.81)
Prin integrarea
relatiei (11.79), cu (11.80) si 11.81), se obtine distributia de presiuni pentru ![]()
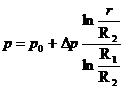 . (11.82)
. (11.82)
Rezulta forta portanta
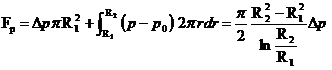 . (11.83)
. (11.83)
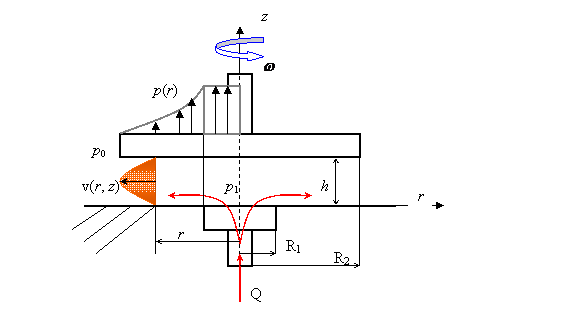
Fig. 11.10. Miscarea unui fluid in lagarul axial hidrostatic.
Pentru determinarea debitului de alimentare Q se
observa ca miscarea este axial simetrica, componentele de
viteza ![]() si
si ![]() sunt independente, iar vz este nul, deci
sunt independente, iar vz este nul, deci
![]() , (11.84)
, (11.84)
ecuatiile (11.25)1 si (11.26) avand expresiile
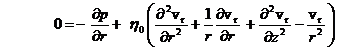 , (11.85)
, (11.85)
![]() , (11.86)
, (11.86)
unde fortele masice se considera neglijabile.
Din (11.85) (11.86) se obtine ecuatia
![]() . (11.87)
. (11.87)
Deoarece presiunea este independenta de axa z, solutia ecuatiei (11.87) este de forma (11.65) in care se introduc conditiile de aderenta pe cele doua discuri; in final distributia de viteza este
![]() . (11.88)
. (11.88)
Din (11.88) si (11.84) rezulta
![]() ; (11.89)
; (11.89)
folosind (11.82) se obtine
expresia debitului transportat intre discuri datorita diferentei de
presiune ![]() ,
,
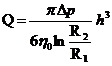 . (11.90)
. (11.90)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |