1. FRECAREA SI LEGILE EI
Legile si proprietatile fortei de frecare sunt enuntate intr-o forma aproximativa in manualele de liceu. In cele ce urmeaza prezentam o exprimare mai nuantata a lor:
1. Forta de frecare la alunecare NU depinde de ARIA suprafetei de contact.
2. Forta de frecare la alunecare este direct proportionala cu FORTA DE APASARE NORMALA.
3. Forta de frecare la alunecare depinde de NATURA si de RUGOZITATEA (gradul de prelucrare) suprafetelor aflate in contact.
4. Forta de frecare la alunecare este mai mare decat forta de frecare la rostogolire.
5. Forta de frecare este orientata in sens opus miscarii; in caz de repaus relativ, ea este orientata in sens opus TENDINTEI INSTANTANEE DE MISCARE.
In cele ce urmeaza ne vom ocupa de cateva chestiuni interpretative legate de frecare.
A doua din legile enuntate mai sus se intalneste in manuale sub urmatorul enunt matematic:
( 1.1 ) Ff = m N.
Precizam de la inceput ca relatia anterioara este corecta dar INCOMPLETA. Sa o analizam mai in detaliu, pornind de la urmatoarea situatie:
Fie un corp de masa m = 10 kg care se poate misca cu frecare ( m = 0,1 ) pe o suprafata orizontala. Vom considera g = 10 m/s2, fara ca prin aceasta aproximatie sa influentam concluziile la care vom ajunge.
Deoarece corpul se poate misca NUMAI PE ORIZONTALA, forta de apasare normala este egala cu greutatea:
( 1.2 ) N = G, deci NUMERIC:
( 1.3 ) N = 100 N.
Inlocuind aceasta valoare in relatia ( 1.1 ) gasim:
( 1.4 ) Ff = 10 N.
Sa presupunem ca actionam asupra corpului cu o forta F = 1 N paralela cu suprafata de contact (vezi fig. 1.1). Ca efect (al principiului actiunilor reciproce) asupra corpului actioneaza o forta de frecare orientata IN SENS OPUS fortei F (vezi fig. 1.2 in care NU am reprezentat fortele normale pe suprafata de contact dintre corpuri).
Conform relatiei ( 1.4 ) aceasta este de 10 N. Rezultanta dintre forta F si cea de frecare are valoarea de 9 N fiind orientata in sens opus fortei F.
Aceasta AR insemna ca, sub actiunea celor doua forte, corpul incepe sa se miste
ACCELERAT IN SENSUL FORTEI DE FRECARE !!
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Fig. 1.1 Fig. 1.2
Sa gasim care a fost greseala din precedentul rationament.
Vom porni de la faptul cunoscut conform caruia frecarea este o forta DE REACTIUNE ( reactiunea asperitatilor microscopice ale suprafetelor de contact la forta de tractiune).
Pornind de la aceasta observatie, este evident ca, daca ACTIUNEA este de 1 N si reactiunea va fi tot de 1 N !!
Daca actiunea va fi de 2, 3, 4, ,10 ( N ), reactiunile corespunzatoare vor avea aceleasi valori (de 2, 3, 4, ,10). Aceasta egalitate se va respecta pana cand actiunea ajunge la 10 N. Am ajuns, pentru FORTA DE TRACTIUNE la valoarea limita pentru care corpul isi mai pastreaza starea initiala de miscare (repaus relativ).
Marind valoarea fortei de tractiune, apare situatia de rupere a contactului intre asperitatile suprafetelor aflate in contact. Aceasta inseamna ca forta de frecare NU POATE LUA VALORI MAI MARI decat o valoare MAXIMA, caracteristica fiecarei PERECHI de corpuri aflate in contact.
Rezulta ca, utilizand relatia ( 1.1 ) vom calcula valoarea maxima a fortei de frecare, ea putand lua valori DE LA ZERO pana la aceasta VALOARE MAXIMA. Aceasta constatare ne permite sa reformulam exprimarea matematica a acestei legi a frecarii:
( 1.5 ) ![]()
Pentru a cuprinde atat cazurile de repaus relativ, cat si cele de miscare relativa, vom utiliza urmatoarea exprimare:
a) in caz de repaus relativ:
![]() , in care produsul ( mN ) reprezinta
valoarea MAXIMA a fortei
de frecare. Aceasta valoare se
atinge in cazul LIMITA de repaus al corpului pe suprafata de sprijin.
, in care produsul ( mN ) reprezinta
valoarea MAXIMA a fortei
de frecare. Aceasta valoare se
atinge in cazul LIMITA de repaus al corpului pe suprafata de sprijin.
b) in caz de miscare relativa:
Ff = m N.
In cele ce urmeaza, ne vom ocupa de cea de-a cincea lege enuntata mai sus.
Sunt numeroase cazurile in care, pentru studiul unui fenomen fizic este necesara precizarea SENSULUI in care este orientata forta de frecare. Dificultati apar in situatiile in care corpul studiat se afla IN REPAUS fata de suprafata pe care este asezat, dat fiind ca la nivelul la care sunt expuse fenomenele fizice in acele lucrari accesibile majoritatii elevilor se trateaza de obicei cazul miscarii relative.
Tinand seama de faptul ca FRECAREA ESTE O FORTA DE REACTIUNE, dificultatea semnalata se poate depasi utilizand urmatorul rationament:
- ne imaginam ca NU ar exista frecare.
daca in aceasta situatie, sub actiunea fortelor aplicate, corpul s-ar misca accelerat intr-un ANUMIT sens, acesta reprezinta sensul TENDINTEI INSTANTANEE DE MISCARE.
- deci frecarea va fi orientata IN SENS OPUS sensului acceleratiei.
- daca sub actiunea fortelor aplicate corpul isi va pastra starea de miscare, frecarea va fi nula.
Vom exemplifica o astfel de situatie prin urmatoarea:
PROBLEMA
Pe o masa orizontala poate aluneca un corp care are masa M = 2,00 kg. Coeficientul de frecare la alunecare are valoarea m = 0,2. La marginile mesei sunt prinsi doi scripeti ideali, peste care se trece cate un fir inextensibil si cu masa neglijabila. Fiecare fir este legat de corpul M, care se afla pe dreapta care uneste cei doi scripeti. Capatul liber al unui fir sustine un corp cu masa m1 = 1,00 kg. De capatul liber al celuilalt fir este prins un platan de masa m2 = 0,10 kg.
Pentru ce valori mx ale maselor marcate asezate pe platan sistemul poate fi in repaus? Se va considera g = 9,8 m/s2.
SOLUTIE
Prima constatare este ca greutatea plata-
nului fara mase marcate este mai mica decat gre-
utatea lui m1:
![]() G1 = m1g
= 9,80 N M
G1 = m1g
= 9,80 N M
![]()
![]()
![]()
![]() G2 = m2g
= 0,98 N
G2 = m2g
= 0,98 N
![]()
![]()
![]() Aceasta inseamna
ca, lasat liber, sistemul
Aceasta inseamna
ca, lasat liber, sistemul
se va misca in sensul coborarii lui m1.
![]()
![]()
![]() Consideram
ca, printr-un mijloc oarecare m1
Consideram
ca, printr-un mijloc oarecare m1
![]()
![]()
![]()
![]() putem mari in mod continuu masa
corpurilor ase- m2
putem mari in mod continuu masa
corpurilor ase- m2
zate pe platan. Apare evident faptul ca, o data cu fig. 1.3
marirea masei (m1 + mx), acceleratia sistemului
scade. Pentru o valoare totala (m1 + mmin) a masei atarnate de acest capat al firului, acceleratia sistemului atinge valoarea ZERO. Este situatia LIMITA de echilibru.
Se pune intrebarea:
- in acest caz in ce sens este orientata forta de frecare ?
Pentru a raspunde la aceasta, ne imaginam ca nu exista frecare. In acest caz, sistemul s-ar misca in sensul URCARII platanului. Acesta este sensul TENDINTEI INSTANTANEE DE MISCARE.
Deoarece forta de frecare reprezinta reactiunea asperitatilor suprafetei de sprijin, rezulta ca ea va fi orientata in sens opus tendintei de miscare a sistemului.
Situatia aflata in discutie este reprezentata in figura 1.4
Considerand ca SENS POZITIV sensul tendintei instantanee de miscare vom scrie, conform principiului inertiei ca:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ( 1.6 )
( 1.6 ) ![]() M
M
si scalar, cu proiectiile fortelor:
( 1.7 ) G1 G2 GX Ff = 0 de unde: m1
( 1.8 ) GX = G1 G2 Ff in care: fig.1.4 m1 + mmin
( 1.9 ) GX = g mmin; G1 = m1g; G2 = m2g; Ff = mMg.
Inlocuind expresiile ( 1.9 ) in ( 1.8 ), dupa efectuarea calculelor se obtine pentru masa minima valoarea:
( 1.10 ) mmin = 0,50 kg.
Rationand analog, atunci cand pe platan se afla masa maxima pentru care sistemul studiat mai poate ramane in repaus, obtinem valoarea MAXIMA pentru corpul mx:
( 1.11 ) mmax = 1,30 kg.
Coreland rezultatele furnizate de relatiile ( 1.10 ) si ( 1.11 ) scriem ca, pentru ca sistemul considerat sa poata indeplini conditiile cerute de textul problemei, masa asezata pe platan trebuie sa apartina intervalului inchis:
( 1.12 ) mx ![]() [ 0,50; 1,30 ] kg.
[ 0,50; 1,30 ] kg.
Pentru fixarea acestor deprinderi de analiza a unor fenomene legate de frecare, vom mai studia o:
PROBLEMA
Pe un plan inclinat care formeaza unghiul a = 300 cu orizontala poate aluneca cu frecare ( m = 0,15 ) un corp cu masa M = 2,00 kg. In varful planului este fixat un scripete ideal peste care este trecut un fir inextensibil
si de greutate neglijabila. Un capat al firului

![]() este prins de corpul M,
celalalt capat sustine
este prins de corpul M,
celalalt capat sustine

![]() un alt corp a carui
masa este m.
un alt corp a carui
masa este m.
![]()
![]() Se cere
acceleratia sistemului si ten- M
Se cere
acceleratia sistemului si ten- M
![]()
![]()
![]()
![]() siunea in fir in
cazurile: m
siunea in fir in
cazurile: m
![]() a) m1
= 0,60 kg
a) m1
= 0,60 kg
b) m2 = 1,20 kg. a
![]() Se va considera g = 9,80 m/s2 fig.1.5
Se va considera g = 9,80 m/s2 fig.1.5
SOLUTIE:
Deoarece NU cunoastem sensul in care se va misca sistemul, (ceea ce ne-ar permite sa tinem seama de frecare), vom determina mai intai proiectiile fortelor aplicate pe directia posibilitatii de miscare permisa de legaturi.
Este vorba de componenta tangentiala a greutatii corpului M:
( 1.13 ) Gt = Mg sin (a) = 9,8 N
si de greutatea lui m1, greutate care, pentru cele doua cazuri are valorile:
( 1.14 ) G1 = 5,88 N respectiv:
( 1,15 ) G2 = 11,76 N.
In primul caz Gt![]() > G1, deci TENDINTA INSTANTANEE DE
MISCARE va fi IN JOS PE PLANUL
INCLINAT. Aceasta inseamna ca forta de frecare va fi
orientata IN SUS PE PLANUL
INCLINAT. Este situatia reprezentata in fig. 1.6 unde NU am
figurat perechea de forte ACTIUNE REACTIUNE (normale pe
suprafata de contact).
> G1, deci TENDINTA INSTANTANEE DE
MISCARE va fi IN JOS PE PLANUL
INCLINAT. Aceasta inseamna ca forta de frecare va fi
orientata IN SUS PE PLANUL
INCLINAT. Este situatia reprezentata in fig. 1.6 unde NU am
figurat perechea de forte ACTIUNE REACTIUNE (normale pe
suprafata de contact).
Pentru a gasi acceleratia sistemului de corpuri fata de un observator exterior (S.R.I. exterior) utilizam METODA IZOLARII CORPURILOR.
Aceasta consta in urmatoarele:
- ne imaginam ca taiem fiecare fir, inlocuind actiunea firelor asupra corpurilor cu cate o forta atat de mare si astfel orientata incat starea de miscare a fiecarui corp sa NU se modifice in urma taierii (mintale) a firelor.
Sa izolam fiecare corp. Pentru corpul M am reprezentat in fig. 1.6 fortele care actioneaza asupra lui, tinand seama ca fiecare este orientata in sus pe planul inclinat. Conform principiului fundamental al dinamicii, vom scrie:
( 1.16 ) Ma1 = Mg sin(a) - mMg cos (a) T1
Izoland corpul m1 (vezi fig.1.7) explicitam (scalar) principiul fundamental al dinamicii sub forma:
( 1.17 ) m1a1 = T1 m1g.

![]() (+)
(+) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]() (+)
(+) ![]()

![]()
![]()
![]()
![]()
fig.1.6 fig 1.7
Cu ultimele doua relatii putem forma un sistem de ecuatii care, rezolvate in raport cu necunoscutele a si T1 ne conduc la rezultatele numerice.
SOLUTIE:
Deoarece NU cunoastem sensul in care se va misca sistemul, (ceea ce ne-ar permite sa tinem seama de frecare), vom determina mai intai proiectiile fortelor aplicate pe directia posibilitatii de miscare permisa de legaturi.
Este vorba de componenta tangentiala a greutatii corpului M:
( 1.13 ) Gt = Mg sin (a) = 9,8 N
si de greutatea lui m1, greutate care, pentru cele doua cazuri are valorile:
( 1.14 ) G1 = 5,88 N respectiv:
( 1,15 ) G2 = 11,76 N.
In primul caz Gt![]() > G1, deci TENDINTA INSTANTANEE DE
MISCARE va fi IN JOS PE PLANUL
INCLINAT. Aceasta inseamna ca forta de frecare va fi
orientata IN SUS PE PLANUL
INCLINAT. Este situatia reprezentata in fig. 1.6 unde NU am
figurat perechea de forte ACTIUNE REACTIUNE (normale pe
suprafata de contact).
> G1, deci TENDINTA INSTANTANEE DE
MISCARE va fi IN JOS PE PLANUL
INCLINAT. Aceasta inseamna ca forta de frecare va fi
orientata IN SUS PE PLANUL
INCLINAT. Este situatia reprezentata in fig. 1.6 unde NU am
figurat perechea de forte ACTIUNE REACTIUNE (normale pe
suprafata de contact).
Pentru a gasi acceleratia sistemului de corpuri fata de un observator exterior (S.R.I. exterior) utilizam METODA IZOLARII CORPURILOR.
Aceasta consta in urmatoarele:
- ne imaginam ca taiem fiecare fir, inlocuind actiunea firelor asupra corpurilor cu cate o forta atat de mare si astfel orientata incat starea de miscare a fiecarui corp sa NU se modifice in urma taierii (mintale) a firelor.
Sa izolam fiecare corp. Pentru corpul M am reprezentat in fig. 1.6 fortele care actioneaza asupra lui, tinand seama ca fiecare este orientata in sus pe planul inclinat. Conform principiului fundamental al dinamicii, vom scrie:
( 1.16 ) Ma1 = Mg sin(a) - mMg cos (a) T1
Izoland corpul m1 (vezi fig.1.7) explicitam (scalar) principiul fundamental al dinamicii sub forma:
( 1.17 ) m1a1 = T1 m1g.

![]() (+)
(+) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() (+)
(+) ![]()

![]()
![]()
![]()
![]()
fig.1.6 fig 1.7
Cu ultimele doua relatii putem forma un sistem de ecuatii care, rezolvate in raport cu necunoscutele a si T1 ne conduc la solutia numerica a problemei.
2. UNGHIUL DE FRECARE
Fie un corp asezat pe un plan inclinat, plan a carei inclinare fata de orizontala poate fi modificata:
( 2.1 ) a ![]() [ 0 ; 900 ]
[ 0 ; 900 ]
Sa ne imaginam ca marim foarte incet inclinarea planului. Ca efect, creste componenta tangentiala a greutatii. Tinand seama de cele expuse mai sus, anume ca forta de frecare este o forta DE REACTIUNE, este evident faptul ca si aceasta va creste de la zero, fiind in fiecare moment EGALA CU GREUTATEA TANGENTIALA.
De asemenea, am precizat ca frecarea nu poate creste oricat, ci numai pana la valoarea maxima data de relatia ( 1.5 ).
Rezulta ca exista o valoare maxima a unghiului format de planul inclinat, unghi pentru care corpul studiat MAI POATE ramane in repaus pe planul inclinat.
Acest unghi il numim UNGHI DE FRECARE (notat cu simbolul ![]() ). Aceasta situatie este
reprezentata in fig. 2.1.
). Aceasta situatie este
reprezentata in fig. 2.1.
Conditia LIMITA de echilibru se exprima ![]() prin conditia:
prin conditia:

![]() ( 2.2 ) Gt = Ff in care:
( 2.2 ) Gt = Ff in care: ![]()

![]() ( 2.3 ) Gt = mg sin(
( 2.3 ) Gt = mg sin(![]() ) si
) si ![]()
( 2.4 ) Ff = ![]() mg cos(
mg cos(![]() ). fig.2.1
). fig.2.1
Inlocuind ultimele doua relatii in ( 2.2 ), dupa efectuarea unor calcule elementare se gaseste:
( 2.5 ) m = tg(![]() ).
).
In multe probleme (a caror
rezolvare necesita cunoasterea coeficientului de frecare) se
precizeaza valoarea unghiului de frecare. Ultima relatie ne
permite cunoasterea lui m atunci cand se cunoaste ![]() (si reciproc).
(si reciproc).
3. CONUL DE FRECARE
Metodele 'clasice' de rezolvare a problemelor in care intervine frecarea sunt, de cele mai multe ori greoaie, deoarece proiectarea fortelor pe axele unui sistem de coordonate convenabil ales ne conduce la rezolvarea unui sistem de ecuatii, rezolvare care uneori necesita calcule destul de laborioase.
In cele ce urmeaza vom prezenta si exemplifica o metoda care, evitand aceste dificultati de calcul, permite uneori SCRIEREA DIRECTA A REZULTATULUI
Pentru aceasta, trebuie sa definim ceea ce, in literatura de specialitate se numeste 'conul de frecare
Precizam ca in rationamentele (si figurile) urmatoare vom reprezenta doar fortele ACTIVE, nu si reactiunile.
PRECIZARE: forta de frecare este - dupa cum am aratat mai sus - o forta de reacti-une!
Fie un corp asezat pe o
suprafata orizontala. Asupra lui actioneaza forta
![]() egala cu forta de frecare MAXIMA posibila
in conditiile date.
egala cu forta de frecare MAXIMA posibila
in conditiile date.
Ea se considera cuprinsa intr-un plan paralel cu suprafata de contact dintre corp si suprafata de sprijin.
Rezultanta dintre greutatea corpului![]() si aceasta forta
si aceasta forta ![]() , formeaza cu NORMALA la suprafata de contact
unghiul b
, formeaza cu NORMALA la suprafata de contact
unghiul b
In cele ce urmeaza ne propunem
sa demonstram ca acest unghi este egal cu unghiul de frecare ![]() . Pentru aceasta vom exprima functia tangenta a
unghiului b
. Pentru aceasta vom exprima functia tangenta a
unghiului b
( 3.1 ) ![]()
in care, deoarece forta F are valoarea MAXIMA pentru care NU se schimba starea de miscare a corpului studiat:
( 3.2 ) F = mG
Inlocuind ( 3.2 ) in ( 3.1 ) si apoi tinand seama de relatia ( 2.5 ) rezulta ca:
( 3.3 ) b = ![]() .
.
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
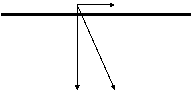
b
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
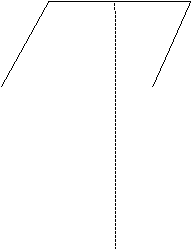
fig.3.1 fig.3.2
Sa ne imaginam ce se intampla daca forta ![]() SE ROTESTE in jurul punctului sau de aplicatie
intr-un plan PARALEL CU SUPRAFATA DE CONTACT dintre corpul studiat si
suprafata de sprijin.
SE ROTESTE in jurul punctului sau de aplicatie
intr-un plan PARALEL CU SUPRAFATA DE CONTACT dintre corpul studiat si
suprafata de sprijin.
Rezultanta dintre aceasta forta si greutatea corpului se va roti in jurul normalei la suprafata de contact, descriind suprafata unui con.
Acesta se numeste : CONUL DE FRECARE
Analiza figurii 3.2 ne permite sa formulam urmatoarele:
Proprietati ale conului de frecare
a) daca rezultanta fortelor aplicate cade IN EXTERIORUL conului de frecare ![]() atunci corpul studiat
se va misca ACCELERAT.
atunci corpul studiat
se va misca ACCELERAT.
b) daca rezultanta
fortelor aplicate cade PE GENERATOAREA conului de frecare ![]() atunci corpul
studiat ISI VA PASTRA
STAREA DE MISCARE.
atunci corpul
studiat ISI VA PASTRA
STAREA DE MISCARE.
c) daca rezultanta fortelor aplicate cade IN INTERIORUL conului de frecare ![]() atunci corpul studiat
se va misca INCETINIT PANA LA OPRIRE.
atunci corpul studiat
se va misca INCETINIT PANA LA OPRIRE.
4. APLICATII
In cele ce urmeaza ne propunem sa aplicam acest model la rezolvarea unor probleme in care intervin forte de frecare.
La cateva probleme vom prezenta si o metoda 'clasica' de rezolvare cu scopul de a facilita comparatia intre cele doua metode.
4.1 Pe o suprafata orizontala un corp se poate misca cu frecare. Cunoscand unghiul de frecare j sa se determine unghiul b sub care o forta MINIMA constanta trebuie sa actioneze asupra corpului pentru ca acesta sa se deplaseze UNIFORM.
METODA I
Conform principiului inertiei, corpul se misca UNIFORM daca suma vectoriala a fortelor care actioneaza asupra lui este NULA.
In cazul aflat in studiu, fortele aplicate sunt (vezi fig. 4.1):
- greutatea proprie ![]() ,
,
- reactiunea normala ![]() ,
, ![]()
![]()
![]() - forta
activa
- forta
activa ![]() si
si ![]()
![]()
![]()
![]()
![]()
![]() - forta de
frecare
- forta de
frecare ![]()
![]()
![]()
![]() Consideram corpul
ca fiind punctiform
Consideram corpul
ca fiind punctiform ![]()
![]()
![]()
![]() si un sistem de axe de coordonate cu originea
si un sistem de axe de coordonate cu originea
in punctul in care se afla corpul. Axele acestuia
sunt
orientate dupa cum urmeaza: ![]()
- axa OX pe directia de deplasare a cor-
pului si
- axa OX pe directia normalei la supra- fig.4.1.1
fata de contact.
Descompunem forta ![]() in doua componente orientate de-a lungul celor doua
axe considerate:
in doua componente orientate de-a lungul celor doua
axe considerate:
( 4.1.1 ) ![]()
forte ale caror module se pot calcula cu ajutorul relatiilor:
( 4.1.2 ) Fx = F cos (b) respectiv:
( 4.1.3 ) Fy = F sin(b
Deoarece pentru valoarea fortei de frecare la alunecare in caz de miscare relativa putem scrie:
( 4.1.4 ) R = mN,
in care N reprezinta modulul fortei de apasare normala, forta care, conform fig. 4.1.1 satisface egalitatea:
( 4.1.5 ) N = G - Fy ,
rezulta, pentru forta de frecare:
( 4.1.6 ) R = m ( G - Fy ) ,
si explicit, cu notatia ( 4.1.3 ) gasim:
( 4.1.7 ) R = m [G - F sin (b
Miscarea uniforma fiind conditionata de indeplinirea egalitatii:
( 4.1.8 ) Fx = R,
procedam la inlocuirea in ( 4.1.8 ) a egalitatilor ( 4.1.2 ) si ( 4.1.7 ) pentru a obtine:
( 4.1.9 ) F cos(b m [G - F sin (b
relatie
din care se poate explicita modulul fortei ![]() . Tinand seama de relatia ( 2.5 ) in care
exprimam functia tg(b) ca fiind raportul dintre sin(b) si cos (b), dupa efectuarea unor
calcule elementare obtinem:
. Tinand seama de relatia ( 2.5 ) in care
exprimam functia tg(b) ca fiind raportul dintre sin(b) si cos (b), dupa efectuarea unor
calcule elementare obtinem:
( 4.1.10 ) ![]() .
.
In aceasta relatie numaratorul este o marime CONSTANTA. Singura marime VARIABILA este unghiul b (care apare in expresia de la numitor . Rezulta ca fractia atinge un MINIM daca numitorul este MAXIM. Deoarece numitorul este o functie armonica, valoarea acestui maxim este egala cu unitatea:
( 4.1.11 ) cos (b-![]() ) = 1,
) = 1,
si aceasta are loc daca:
( 4.1.12 ) b = j
Interpretarea fizica a acestei egalitati este urmatoarea.
Forta MINIMA care deplaseaza UNIFORM corpul, trebuie sa formeze cu orizontala un unghi egal cu unghiul de frecare.
METODA II
In fig. 4.1.2 am reprezentat
greutatea ![]() a corpului asezat
pe suprafata de sprijin precum si conul de frecare. Acesta are axa de
simetrie normala pe suprafata de contact.
a corpului asezat
pe suprafata de sprijin precum si conul de frecare. Acesta are axa de
simetrie normala pe suprafata de contact.
![]() Conform celor expuse
mai sus, pentru
Conform celor expuse
mai sus, pentru
 a deplasa UNIFORM corpul, rezultanta din-
a deplasa UNIFORM corpul, rezultanta din- ![]()
![]()
![]()
![]() tre greutatea
tre greutatea ![]() si forta
si forta ![]() aplicata din
exteri- b
aplicata din
exteri- b
![]()

![]()
![]()

![]() or sub unghiul b trebuie sa cada pe generatoa-
or sub unghiul b trebuie sa cada pe generatoa-
rea conului de frecare
![]() Vom determina GRAFIC
rezultanta a-
Vom determina GRAFIC
rezultanta a-
![]() cestor doua forte utilizand regula triunghiului:
cestor doua forte utilizand regula triunghiului: ![]()
deplasam
vectorul forta ![]() paralel cu el
insusi
paralel cu el
insusi ![]()
![]()
![]()
 pana cand punctul lui de
aplicatie coincide cu
pana cand punctul lui de
aplicatie coincide cu ![]()
varful vectorului greutate. ![]() b
b
![]()
![]()
![]() Atunci, vectorul care are originea in
Atunci, vectorul care are originea in
punctul de aplicatie al greutatii si extremita-
tea in varful fortei aplicate, este vectorul forta
TOTALA. Pentru cazul studiat, acest vector
trebuie sa fie orientat pe directia generatoarei fig. 4.1.2
conului de frecare
Reamintim ca in cadrul acestui model studiem numai fortele active NU si reactiunile.
Exista o infinitate de vectori care unesc varful greutatii cu panza conului de frecare. Dintre acestia, valoarea MINIMA o are vectorul care este NORMAL pe suprafata interioara a conului (vezi fig. 4.1.2).
Unghiul format de acest vector, cu
un plan orizontal care include punctul lui de aplicatie, este unghiul b cautat. Studiul
geometric al figurii 4.1.2 pune in evidenta perpendicularitatea
laturilor unghiurilor b si ![]() , deci solutia problemei este:
, deci solutia problemei este:
( 4.1.13 ) b = j.
Am ajuns la acelasi rezultat ca si in cazul primei metode, dar FARA A FI NECESARE CALCULE !!! Mai este necesara comparatia intre cele doua metode?
4.2 Pentru un
container asezat pe un plan inclinat la a = 300,
unghiul de frecare este ![]() = 150
si considerand acceleratia gravitationala g = 9,8 m/s, se
cere valoarea acceleratiei cu care containerul coboara liber planul
inclinat.
= 150
si considerand acceleratia gravitationala g = 9,8 m/s, se
cere valoarea acceleratiei cu care containerul coboara liber planul
inclinat.
METODA - l
Utilizand relatia cunoscuta pentru acceleratia cu care un corp lasat liber pe un plan inclinat coboara pe acesta:
( 4.2.1 ) ac = g [ sin(a) - cos(a) ],
dupa
inlocuirea numerica in care exprimam pe m ca fiind tg(![]() ), obtinem pentru acceleratie o valoare
NEGATIVA :
), obtinem pentru acceleratie o valoare
NEGATIVA :
( 4.2.2 ) ac = 0,57 m/s2.
Interpretarea fizica a semnului minus AR FI aceea ca, de fapt, corpul URCA PE PLA-NUL INCLINAT.
Deoarece un asemenea fenomen NU poate avea loc de la sine, rezulta ca in conditiile problemei corpul nu isi poate schimba starea de miscare, (va ramane in repaus relativ pe plan).
Aceasta situatie apare deoarece componenta tangentiala a greutatii este mai mica decat forta de frecare MAXIMA corespunzatoare situatiei date.
La acelasi rezultat se poate ajunge, mai simplu, cu:

 METODA - 2
METODA - 2
![]()
![]() Am reprezentat in fig.
4.2.1 greutatea
Am reprezentat in fig.
4.2.1 greutatea


![]()
![]() a corpului si conul de frecare cu axa de
a corpului si conul de frecare cu axa de
![]() simetrie NORMALA PE
SUPRAFATA DE
simetrie NORMALA PE
SUPRAFATA DE
![]()
![]()
![]() CONTACT. Deoarece, conform textului pro- a
CONTACT. Deoarece, conform textului pro- a ![]()
![]() blemei:
blemei: ![]() > a, greutatea corpului cade IN
> a, greutatea corpului cade IN
 INTERIORUL conului de frecare. Aceasta a
INTERIORUL conului de frecare. Aceasta a
inseamna ca, in general, corpul se va misca
incetinit pana la oprire. In cazul particular in ![]()
care initial corpul era in repaus (cazul proble-
![]() mei studiate), el va ramane nemiscat pe pla-
mei studiate), el va ramane nemiscat pe pla-
nul inclinat.
fig. 4.2.1
4.3 Un corp asezat pe o suprafata orizontala este tras de o forta data, forta care formeaza cu directia de miscare unghiul a. Unghiul de frecare fiind j = 180, pentru ce valoare a lui a acceleratia va fi maxima?
Corpul studiat se va misca accelerat daca rezultanta dintre greutatea proprie ![]() si
forta aplicata
si
forta aplicata ![]() (constanta in
modul) cade IN EXTERIORUL conului de frecare.
(constanta in
modul) cade IN EXTERIORUL conului de frecare.


![]()
![]() Mai mult decat atat,
acceleratia va fi
Mai mult decat atat,
acceleratia va fi
![]() cu atat mai mare in modul, cu cat
aceasta
cu atat mai mare in modul, cu cat
aceasta
rezultanta va iesi mai mult din panza conu-
lui (in exterior). Utilizand regula triunghiu-
lui pentru compunerea celor doua forte apli- j
![]() cate, extremitatea vectorului
cate, extremitatea vectorului ![]() se gaseste
se gaseste

![]() pe circumferinta unui cerc
ce are centrul in
pe circumferinta unui cerc
ce are centrul in ![]()
![]() varful greutatii.
Acest vector va iesi cel mai
varful greutatii.
Acest vector va iesi cel mai ![]()
mult din con, daca este perpendicular pe o a
![]()
![]()
![]() generatoare.
generatoare.
In acest caz, unghiul format de ![]() cu
cu
![]()
![]() orizontala va fi:
fig.4.3.1
orizontala va fi:
fig.4.3.1
( 4.3.1 ) a = ![]()
4.4 O
caramida cu greutatea G = 25 N trebuie tinuta
lipita de un perete vertical. Sa se calculeze forta de
apasare normala stiind ca unghiul de frecare este ![]()
Vom considera caramida ca fiind un punct material, punct in care plasam varful conului de frecare. Axa de simetrie a conului, (in general - normala pe suprafata de contact) este orizontala - in cazul problemei aflata in studiu.
 Conditia
limita de echilibru a corpului pe perete se indeplineste atunci cand
rezultanta dintre greutatea proprie
Conditia
limita de echilibru a corpului pe perete se indeplineste atunci cand
rezultanta dintre greutatea proprie ![]() a caramizii
si forta
a caramizii
si forta ![]() de apasare
normala pe perete este
orientata pe directia generatoarei conului de frecare.
de apasare
normala pe perete este
orientata pe directia generatoarei conului de frecare.
 Deoarece, in acest
caz:
Deoarece, in acest
caz:
![]() ( 4.4.1 )
( 4.4.1 ) ![]() ,
,
![]()
![]()
![]()
![]() rezulta ca:
rezulta ca:
![]()
![]()
![]()
![]()
si numeric:
( 4.4.3 ) ![]() . fig.4.4.1
. fig.4.4.1
4.5 O lada este tarata uniform in sus pe un plan inclinat. Forta necesara deplasarii este minima atunci cand unghiul dintre forta si planul inclinat este b = 150.
Aflati unghiul de frecare ce caracterizeaza suprafata de contact dintre lada si planul inclinat.
Fie ![]() rezultanta dintre
rezultanta dintre ![]() si
si ![]() . Pentru
. Pentru
ca lada sa se miste uniform,
rezultanta ![]() trebu-
trebu-
 ie sa fie
orientata dupa generatoarea
conului de
ie sa fie
orientata dupa generatoarea
conului de ![]()
 frecare ( vezi fig. 4.5.1 ). Pentru ca lada sa urce
frecare ( vezi fig. 4.5.1 ). Pentru ca lada sa urce
 uniform planul inclinat, vectorul
uniform planul inclinat, vectorul ![]() trebuie sa
fie b
trebuie sa
fie b
![]()
![]() orientat dupa acea generatoare a conului de fre- a
orientat dupa acea generatoare a conului de fre- a
![]()
![]()
![]() care ce este CEA MAI DEPARTATA de gre-
care ce este CEA MAI DEPARTATA de gre-
utate.
Cea mai mica forta ce, impreuna cu gre-
utatea, da o rezultanta care indeplineste aceasta a
![]()
![]() conditie, este aceea care
este normala pe panza
conditie, este aceea care
este normala pe panza
conului ![]()
![]()
 Ea formeaza cu
orizontala unghiul (a +
Ea formeaza cu
orizontala unghiul (a + ![]() ).
). ![]()
Dar, conform textului, ea este inclinata cu
unghiul b fata de planul inclinat, formand cu ori-
![]()
![]() zontala unghiul a + b. Rezulta ca:
zontala unghiul a + b. Rezulta ca:
( 4.5.1 ) a + b = a + ![]() , de unde
, de unde
( 4.5.2 ) b = j = 150. fig.4.5.1
4.6 Intre ce limite trebuie sa fie cuprinsa acceleratia unui plan inclinat cu a = 450 fata de orizontala pentru ca un colet asezat pe acest plan sa ramana in repaus relativ fata de plan?
Se cunoaste valoarea unghiului de frecare ![]() =
60 pentru suprafata de contact.
=
60 pentru suprafata de contact.
Deoarece ![]() < a, daca planul inclinat
< a, daca planul inclinat
![]()
![]() este in repaus fata de un S.R.I. exterior,
cole-
este in repaus fata de un S.R.I. exterior,
cole-
![]()
 tul va aluneca accelerat catre baza planului.
tul va aluneca accelerat catre baza planului.
Aceasta ne permite sa afirmam ca,
pentru a asigura conditia de
nealunecare pe ![]()
![]()


![]()
![]()
![]() plan, acesta din urma trebuie sa se miste acce-
plan, acesta din urma trebuie sa se miste acce-
lerat spre stanga figurii 4.6.1.
Ca efect, fata de un
S.R.N. solidar cu ![]()
![]()
![]()
![]() planul, asupra coletului, in afara de greutatea
planul, asupra coletului, in afara de greutatea
proprie
![]() , mai actioneaza, pe directia orizon-
, mai actioneaza, pe directia orizon-
tala,
forta de inertie ![]() (ca forta aplicata). Din
(ca forta aplicata). Din ![]()
analiza
figurii 4.6.1 rezulta ca exista DOUA ![]()
![]()
![]()
![]() valori - limita ale
fortei de inertie, valori pen-
valori - limita ale
fortei de inertie, valori pen-
tru care rezultanta:
![]()
( 4.6.1 ) ![]() fig.
4.6.1
fig.
4.6.1
este orientata pe directiile generatoarelor conului de
frecare aflate in plan vertical. Le vom nota cu ![]() respectiv cu
respectiv cu ![]() .
.
In cele doua cazuri, rezultanta
![]() formeaza cu
verticala unghiurile (a - j), respectiv (a j). Putem scrie ca:
formeaza cu
verticala unghiurile (a - j), respectiv (a j). Putem scrie ca:
( 4.6.2 ) ![]() .
.
Explicitand F si G ca fiind:
( 4.2.3 ) F = ma, respectiv G = mg, dupa inlocuirea in ( 4.6.2 ) si simplificarea cu
masa coletului, se obtine:
( 4.6.4 ) ![]() ,
,
ceea ce, dupa inlocuiri si calcule numerice ne conduce la valorile:
( 4.6.5 ) ![]() , respectiv:
, respectiv:
( 4.6.6 ) ![]() .
.
Deci, pentru a asigura conditia de nealunecare a coletului pe planul inclinat, acesta din urma trebuie sa se miste accelerat cu o acceleratie care satisface dubla inegalitate:
( 4.6.7 ) ![]()
4.7 La un viraj cu raza R = 100 m soseaua este inclinata cu unghiul a = 150 fata de orizontala. Din cauza poleiului unghiul de frecare a devenit mai mic decat a. In aceste conditii viteza maxima cu care se poate ataca virajul are valoarea Vmax = 77 Km/h.
Calculati unghiul de frecare si viteza minima corespunzatoare conditiilor problemei.
Un rationament analog celui din problema anterioara ne conduce la afirmatia ca acceleratia centripeta a automobilului trebuie sa satisfaca dubla inegalitate:
( 4.7.1 ) ![]()
in care, pentru acceleratia centripeta consideram expresia cunoscuta:
( 4.7.2 ) ![]() . Cu acestea,
pentru viteza maxima:
. Cu acestea,
pentru viteza maxima:
( 4.7.3 ) ![]() ,
,
de unde:
( 4.7.4 ) a + j = 25,020 = 25001'27'' ![]() 250.
250.
Aceasta ne permite sa calculam unghiul de frecare:
( 4.7.5 ) j = 100.
Pentru a determina viteza minima posibila cu care se poate ataca virajul, consideram prima inegalitate din ( 4.7.1 ):
( 4.7.6 ) ![]() , de unde:
, de unde:
( 4.7.7 ) ![]() ,
,
ceea ce ne conduce la urmatoarea valoare numerica:
( 4.7.8 ) Vmin = 9,26 m/s = 33,34 Km/h.
4.8 Prin suprainaltarea partii exterioare a soselei la viraje cu unghiul a, viteza maxima posibila creste. Sa se afle de cate ori creste viteza maxima, daca a = 100 si j
Pe o sosea cu suprafata orizontala ( fig. 4.8.1 ) vitezei maxime posibile V0 fata de un S.R.N. solidar cu corpul ii corespunde o forta centrifuga de inertie care, impreuna cu greutatea automobilului trebuie sa dea o rezultanta inclinata cel mult cu unghiul j fata de verticala. Deci:
( 4.8.1 ) ![]()
In cazul unei sosele suprainaltate, conditia de nealunecare laterala la viteza maxima se exprima prin:
![]() ( 4.8.2 )
( 4.8.2 ) ![]() ,
,
![]()

![]()
![]()
![]()
![]()
de unde, pentru viteza maxima in aceste conditii:
( 4.8.3 ) ![]()
![]()
Impartind membru cu membru
relatia ( 4.8.3 ) ![]()
la ( 4.8.1 ) se gaseste:
![]()
( 4.8.4 ) 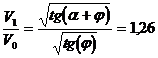 fig. 4.8.1
fig. 4.8.1
In cele ce urmeaza va propunem cateva probleme care, pe langa metode clasice, admit rezolvari-fulger, utilizand notiunea de con de frecare,
1. Pe suprafata interioara a unui trunchi de con, situat cu baza mica in jos, se roteste un mobil cu viteza constanta, traiectoria lui fiind un cerc aflat in plan orizontal. Pentru o anumita valoare a vitezei tangentiale a corpului, acesta este la limita de alunecare catre baza mica (in jos). Daca viteza mobilului se dubleaza, acesta se va afla la limita de alunecare catre baza mare (in sus). Sa se determine valoarea coeficientului de frecare dintre corp si suprafata interioara a corpului, daca unghiul format de generatoare cu baza mica a trunchiului de con este de 1350.
R > μ = 1/3.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |