Daca vom adauga caldura unei probe dintr-un material adesea temperatura acestuia creste. (Daca suntem cumva la temperatura de modificare de stare, de exemplu gheata in apa, temperatura nu se va modifica si va determina doar topirea ghetii.) La distanta de punctul de modificare de faza, orice aport de temperatura va determina intotdeauna o crestere a temperaturii sistemului. Valoarea cu care creste temperatura depinde de cat de multa caldura a fost oferita sistemului, marimii probei, de temperatura initiala a probei si de cum a fost oferita aceasta caldura. Exista doua cai obisnuite prin care i se poate oferii caldura unui sistem, fie mentinand volumul constant, fie mentinand presiunea constanta. Bine inteles ca pot exista si alte cai de a oferii caldura unui sistem, dar acelea nu intra in sfera studiilor noastre.
Sa presupunem acum ca vom adauga
caldura la o proba mentinuta la volum constant,
adica dV = 0. Daca
admitem acum ca q va
reprezenta intotdeauna caldura
absorbita de sistem, q va poate avea valori pozitive sau
negative indicand sensul in care se "scurge" caldura. Daca q este
pozitiv, caldura este intr-adevar absorbita de sistem. Pe de
alta parte daca q are o valoare negativa aceasta
reprezinta faptul ca sistemul cedeaza caldura
vecinatatilor. Fie qV caldura
adaugata (subscrisul V,
indica faptul ca volumul nu variaza la adaugarea
caldurii, ramanand constant). Fie, de asemenea, ΔT modificare
de temperatura. raportul, ![]() , depinde de
material de cantitatea de material a probei si de temperatura. La
limita, atunci cand qV tinde catre zero astfel incat
si ΔT tinde catre zero, acest raport devine o
derivata,
, depinde de
material de cantitatea de material a probei si de temperatura. La
limita, atunci cand qV tinde catre zero astfel incat
si ΔT tinde catre zero, acest raport devine o
derivata,
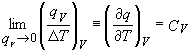 .
(11.1)
.
(11.1)
Acestei derivate i s-a atribuit simbolul de CV, si poate fi numita 'capacitate calorica la volum constant". De obicei se citeaza drept 'capacitate calorica molara'
![]() . (11.2)
. (11.2)
Ecuatia (11.1) se poate acum rearanja sub forma
![]() . (11.3)
. (11.3)
Putem apoi integra aceasta ecuatie pentru a afla caldura implicata intr-o modificare finita la volum constant
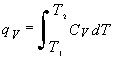 (11.4)
(11.4)
Daca CV este , o constanta aproximativa pentru un domeniu definit de temperatura, atunci CV poate fi extras de sub semnul integrarii iar caldura la volum constant devine
![]() . (11.5)
. (11.5)
Sa urmam aceleasi etape exceptand faptul ca acum vom mentine presiunea constanta in locul volumului constant. Definitia initiala a capacitatii calorice la presiune constanta Cp devine
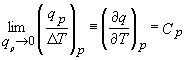 . (11.6)
. (11.6)
capacitatea calorica molara analoga este,
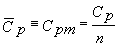 .
(11.7)
.
(11.7)
Ecuatia (11.6) poate fi acum rearanjata sub forma
![]() , (11.8)
, (11.8)
care prin integrare duce la
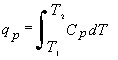 . (11.9)
. (11.9)
Cand Cp este o constanta aproximativa integrala (11.9) devine
![]() .
(11.10)
.
(11.10)
Foarte frecvent domeniul de temperatura este suficient de mare pentru ca Cp sa nu poata fi privit ca o constanta. In aceste cazuri capacitatea calorica este corespunzatoare unei expresii polinomiale a lui T sau a unei functii similare. De exemplu unele tabele dau capacitatea calorica ca fiind
![]() ,
(11.11)
,
(11.11)
unde α , β , si γ sunt constante date in tabel. Prin aceasta dependenta de temperatura, capacitatea calorica la o presiune constanta va trebui sa urmeze calea urmatoarei integrale
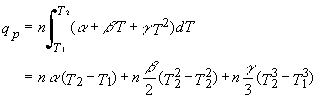 .
(11.12 a, b)
.
(11.12 a, b)
Uneori se mai gasesc diferite forme pentru dependenta de
temperatura a capacitatii calorice sub forma
![]() .
(11.13)
.
(11.13)
Atunci cand veti calcula valori pentru Cp trebuie sa fiti atenti la expresia utilizata pentru
aceasta.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |