
Cama de rotatie si tachet cu miscare de translatie
cu suprafata activa plana.
Metoda I
Se cunosc:
- legea de miscare a camei:
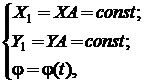 (3.3.19)
(3.3.19)
- legea de miscare a tachetului:
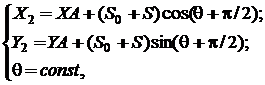 (3.3.20)
(3.3.20)
- ecuatiile parametrice ale profilului tachetului:
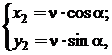 (3.3.21)
(3.3.21)
Se determina:
- ecuatiile parametrice ale profilului camei:
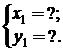
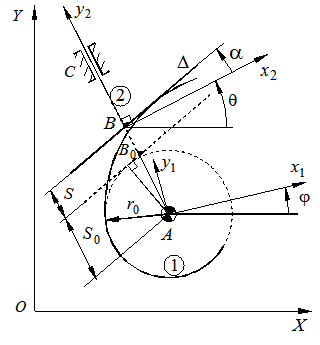
Fig. 3.3.2. Schema cinematica a mecanismului cu cama de rotatie cu tachet de translatie cu suprafata activa plana
Folosind relatiile (3.2.6'), (3.2.8), (3.3.19), (3.3.20) si (3.3.21), rezulta:
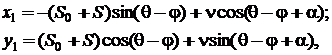 (3.3.22)
(3.3.22)
unde ![]() .
.
Expresia
parametrului de generare ![]() se determina cu
ajutorul relatiei (3.1.8), corespunzatoare conditiei de
tangenta in sistemul
se determina cu
ajutorul relatiei (3.1.8), corespunzatoare conditiei de
tangenta in sistemul ![]() , si anume:
, si anume:
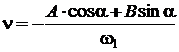 , (3.3.23)
, (3.3.23)
unde: ![]()
Daca
atat numaratorul, cat si numitorul relatiei (3.3.23) se
impart cu ![]() , expresia parametrului de generare
, expresia parametrului de generare ![]() devine:
devine:
![]() , (3.3.24)
, (3.3.24)
unde: 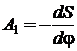 ,
, ![]() , iar
, iar ![]() si
si ![]() sunt functiile de
transmitere de ordinul zero si respectiv de ordinul unu.
sunt functiile de
transmitere de ordinul zero si respectiv de ordinul unu.
Facandu-se inlocuirile in relatiile (3.3.22), se obtin ecuatiile parametrice ale curbei directoare a camei, si anume:
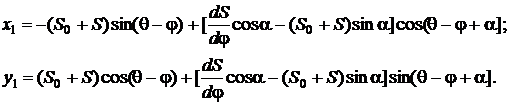 (3.3.25)
(3.3.25)
Raza
minima a camei este: ![]() .
.
Daca
![]() si
si ![]() , relatiile (3.3.25) devin:
, relatiile (3.3.25) devin:
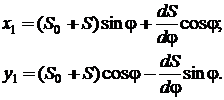 (3.3.26)
(3.3.26)
In acest
caz, raza minima a camei este ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |