
Pentru cunoasterea tipurilor de tranzitii de faza posibile este necesara cunoasterea parametrilor termodinamici de baza, precum si a comportarii unor marimi fizice de interes in vecinatatea valorilor critice a acestora, specifice fiecarei tranzitii de faza.
Datorita masei de repaus mici,
pionul joaca un rol special in dinamica
materiei nucleare fierbinti si dense. La T = 0 se considera
ca pionul este stabil din punct de vedere
hadronic. Pentru T ![]() 0 intervine procesul de dezintegrare a pionului, care conduce
la o largime nenula in partea imaginara a functiei
Green a pionului. Aceasta largime este considerata
ca un coefficient de "atenuare" care poate sa determine divergenta
functiei Green a pionului la temperatura critica de tranzitie
specifica. In general, largimea unui hadron este
un parametru de ordine fenomenologic pentru tranzitia de faza. Cu cresterea
temperaturii hadronii "se topesc", iar largimile lor ar putea creste
pina ar deveni infinite la T = Tc. In aceste
conditii nu vor mai exista maxime de rezonanta in
functia spectrala hadronica, functie care devine o
functie neteda de energie, valoarea sa
coincizind cu cea din cromodinamica cuantica perturbativa.
0 intervine procesul de dezintegrare a pionului, care conduce
la o largime nenula in partea imaginara a functiei
Green a pionului. Aceasta largime este considerata
ca un coefficient de "atenuare" care poate sa determine divergenta
functiei Green a pionului la temperatura critica de tranzitie
specifica. In general, largimea unui hadron este
un parametru de ordine fenomenologic pentru tranzitia de faza. Cu cresterea
temperaturii hadronii "se topesc", iar largimile lor ar putea creste
pina ar deveni infinite la T = Tc. In aceste
conditii nu vor mai exista maxime de rezonanta in
functia spectrala hadronica, functie care devine o
functie neteda de energie, valoarea sa
coincizind cu cea din cromodinamica cuantica perturbativa.
In cadrul algebrei de curenti s-a propus urmatoarea relatie, cunoscuta si ca relatia Gell-Mann - Oakes - Renner :
![]() , (IV.29)
, (IV.29)
unde fë![]() 93 MeV, <q*q> = <u*u>=<d*d>= - 0.01 GeV3. Urmarindu-se realizarea de corectii de temperatura
la relatia de mai sus, se obtine dependenta de temperatura
a masei pionului. Pentru T = 0, functia corespunzatoare are
forma urmatoare:
93 MeV, <q*q> = <u*u>=<d*d>= - 0.01 GeV3. Urmarindu-se realizarea de corectii de temperatura
la relatia de mai sus, se obtine dependenta de temperatura
a masei pionului. Pentru T = 0, functia corespunzatoare are
forma urmatoare:
![]() , (IV.30)
, (IV.30)
Calculul functiei ![]() se face in
cadrul cromodinamicii cuantice perturbative, pina in ordinal
trei in masa cuarcilor, cu luarea in considerare a corectiilor
neperturbative de diferite tipuri. Folosind urmatoarele valori ale unor
marimi care intervin in rezolvarea ecuatiei IV.30 , mu
se face in
cadrul cromodinamicii cuantice perturbative, pina in ordinal
trei in masa cuarcilor, cu luarea in considerare a corectiilor
neperturbative de diferite tipuri. Folosind urmatoarele valori ale unor
marimi care intervin in rezolvarea ecuatiei IV.30 , mu![]() 5 MeV, md
5 MeV, md![]() 10 MeV,
10 MeV, ![]()
![]() (1
(1![]() 4)10-2 GeV4, q2
4)10-2 GeV4, q2![]() 1 GeV2, se obtine expresia de mai jos:
1 GeV2, se obtine expresia de mai jos:
![]()
(IV.31)
Cea mai joasa stare hadronica este pionul; de aceea, din punct de vedere hadronic, saturarea in cea mai joasa stare hadronica conduce la urmatoarea forma:
![]() , (IV.32)
, (IV.32)
Expresia de mai sus se modifica
daca se introduce rezonantele pionice mai inalte; pentru
energii sub 1 GeV este posibila absorbirea
acestora in continuum. Fie s0 pragul de continuum. Folosind
teorema Cauchy pentru ![]() si
si ![]() si regulile de
sumare pentru energii finite se obtin corectiile termice la
temperature finite:
si regulile de
sumare pentru energii finite se obtin corectiile termice la
temperature finite:
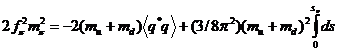 , (IV.33.1)
, (IV.33.1)
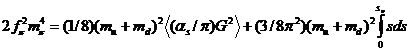 , (IV.33.2)
, (IV.33.2)
iar
partea imaginara a functiei ![]() se poate scrie astfel:
se poate scrie astfel:
![]() (IV.33.3)
(IV.33.3)
cu nF(x) = ( 1 + ex )-1 factorul termic Fermi.
In Fig.IV.4 se prezinta comportarea rapoartelor fë(T)/ fë(0) , <q*q>T/<q*q>0 , s0(T)/s0(0) in functie de temperatura relativa T/Tc. Se observa ca toate cele trei rapoarte au comportari similare pina la T/Tc = 0.8 , iar pentru valori mai mari se constata o scadere rapida, atingindu-se valoarea 0 a raportului pentru T/Tc = 1.2.
Fie ecuatiile:
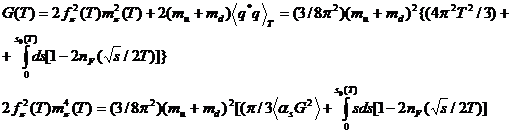 (IV.34)
(IV.34)
.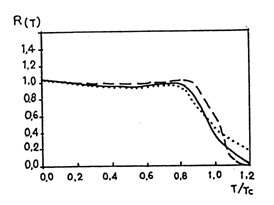
Fig.IV.4. Comportare constantei de dezintegrare, in diverse aproximatii,
in raport cu temperatura relativa
In Fig.IV.5. se reprezinta comportarea raportului G(T)/G(0) pentru s0(0) = 1GeV2. Se constata acelasi tip de comportare ca in Fig.IV.4.
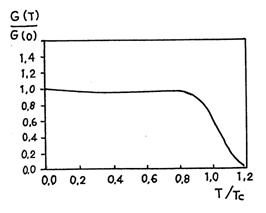
Fig.IV.5. Comportarea raportului G(T)/G(0) in functie de temperaturra relativa
Fig.IV.6 prezinta variatia raportului më(T)/më(0) cu crestera temperaturii relative.Exista mici diferente in valoarea temperaturii relative la care apare cresterea raportului maselor in functie de valorile parametrilor folositi. Aceste rezultate par sa indice ca masa pionului nu se modifica cu cresterea temperaturii regiunii participante pentru temperaturi sub temperatura critica de tranzitie.
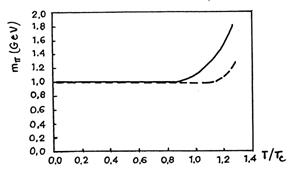
Fig.IV.6. Variatia masei de repaus a pionilor cu cresterea temperaturii relative
Bibliografie
[1]. J.W.Harris et al - Phys.Rev.Lett.47(1981)229
[2]. A.Shor et al - Phys.Rev.Lett.48)1982)1597
[3]. P.Koch et al - Phys.Rev.C40(1989)145
[4]. J.Julien et al - Phys.Lett.B264(1991)269
[5]. M.Belkacem, E.Suraud, S.Ayik - Phys.Rev.C47(1993)R16
H.Leutwyler, A.V.Smilga - Nucl.Phys.B342(1990)302
[7]. C.A.Dominguez, E.de Rafael - Ann.Phys.174(1987)372
[8]. R.A.Berttmann et al - Z.Phys.C39(1988)231
[9]. A.I.Bochkarev, M.E.Shaposnikov - Nucl.Phys.B268(1986)220
[10]. C.A.Dominguez, M.Loewe - Phys.Rev.D52(1995)3143
V.Metag -
C.Besliu, Nicoleta Ioneci, Al.Jipa, R.Zaharia - Rom.Rep.Phys.48(5,6)(1996)47
Al.Jipa - J.Phys.G: Nucl.Part.Phys.22(1996)231
Al.Jipa, Razvan Ionescu, Nicoleta Ioneci - Rom.Rep.Phys.48(5,6)(1996) 53
[15]. W.Weise - Probing the Nuclear Paradigm - Proceedings of the International School in Heavy Ion Physics, Erice, Italy, 6-16 October 1993
[16]. R.Mattiello et al - Phys.Rev.Lett.63(1989)1459
[17]. P.Vincent et al. - Nucl.Phys.A498(1989)67
[18]. Sa Ben-Hao et al - Phys.Rev.C48(1993)2995
[19]. J.Letessier et al - Phys.Rev.D51(1996)3408
[20]. J.Nambu, G.Jona-Lasinio - Phys.Rev.122(1961)345
[21]. W.Weise - Phys.Lett.B278(1992)29
C.Besliu, Al.Jipa, R.Zaharia - Rom.Rep.Phys.46(1994)389
W.Weise - Phys.Lett.B405(1997)215
[24]. Al.Jipa, C.Besliu, Maria Iosif, R.Zaharia - Il Nuovo Cimento A112(1999)179
[25]. Al.Jipa - Teza de doctorat, Universitatea Bucuresti, Facultatea de Fizica, 1989
[26]. Al.Jipa - Turkish Journal of Physics 19(1995)846
[27].Al.Jipa, C.Besliu, Maria Iosif, R.Zaharia - Quark Matter´96, Heidelberg, Germany, 20-24.V.1996
[28]. C.Besliu, Al.Jipa - Rev.Roum.Phys.33(1988)409
[29]. C.Besliu, Al.Jipa - Rom.J.Phys.37(1992)1011
[30]. C.Besliu et al - The XXVIII International Conference on High Energy Physics, Warsaw (Poland), 25-31.VII.1996, PA06-021
[31]. Al.Jipa, C.Besliu, Maria Iosif, R.Zaharia - The X General Conference of the European Physical Society 'Trends in Physics', Sevilla (Spain), 9-13.IX.1996
[32]. C.Besliu, Al.Jipa - Il Nuovo Cimento A106(1993)317
[33].Al.Jipa - Balkan Physics Letters 1(1993)79
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |