
Exista diferite cai de determinare a caracteristicilor spatio-temporale ale sursei de particule. În cazul modelelor statistico-termodinamic de tip Fermi [68,69] si Hagedorn [70,71] se considera un sistem inchis intr-un volum V; sistemul respecta conditii periodice la capete. Pentru astfel de modele se face presupunerea ca rata de anihilare in orice stare Nπ este data de probabilitate PN(Ω), data de relatia:
PN(Ω)=(Ω/V)N , (II.83)
unde Ω este volumul de reactie; in volumul de reactie se presupune ca se produce amestecul statistic al starilor. Marimea PN(Ω) este considerata probabilitatea de a gasi N pioni liberi in volumul de reactie si este definita prin relatia urmatoare:
![]() , (II.84)
, (II.84)
unde
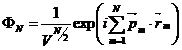 . (II.85)
. (II.85)
Pentru
cazul N=2, cu doua particule
identice, avind impulsurile ![]() si
si ![]() , probabilitatea corespunzatore, P2(Ω), are un rol important. Folosind notatia Ψ(12) pentru aceasta
probabilitate relatia (II.84) se poate scrie in forma urmatoare
pentru cazul mentionat:
, probabilitatea corespunzatore, P2(Ω), are un rol important. Folosind notatia Ψ(12) pentru aceasta
probabilitate relatia (II.84) se poate scrie in forma urmatoare
pentru cazul mentionat:
![]() . (II.86)
. (II.86)
Integrarea se face dupa cele doua variabile pe o sfera Ω=4πρ3/3, iar integrandul are urmatoarea expresie:
![]() . (II.87)
. (II.87)
Prin integrare se obtine, pentru o sursa de forma sferica, urmatoarea expresie a probailitatii definite de relatia (II.86):
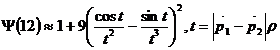 . (II.88)
. (II.88)
Probabilitatea Ψ(12), definita de relatia (II.86), respectiv, relatia (II.88), nu va mai depinde doar de marimea volumului de interactie Ω, ci si de forma. Trebuie mentionat aici faptul ca probabilitatea Ψ(12) pentru un model care considera o sursa sferica, cum este cea data de relatia (II.88), difera foarte putin de probabilitatea Ψ(12) obtinuta pentru cazul in care se presupune o forma gaussiana:
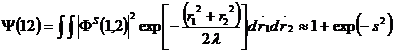 , (II.89.a)
, (II.89.a)
cu
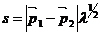 . (II.89.b)
. (II.89.b)
În acest caz se integreaza de doua ori pe intreg spatiul. Calculele se pot simplifica inainte de a se trece la evaluarile numerice [66].
Descoperirea curgerii anizotropice transversale in ciocnirile nucleu-nucleu la energii relativiste (curgerii eliptice)a impus reevaluarea unor cai de determinare a caracteristicilor spatio-temporale ale sursei de particule cu luarea in considerare a efectului de curgere hidrodinamica a materiei nucleare. Determinarea volumului de ciocnire folosind efectul Hanbury-Brown - Twiss si metodele de calcul asociate permite compararea cu rezultatele obtinute prin alte metode, specifice modelelor hidrodinamice pentru ciocniri nucleare relativiste
Analiza efectului Hanbury-Brown si Twiss permite investigarea marimii sursei in mai multe dimensiuni . Acest lucru se poate face studiind dependenta functiei de corelatie, pe diferite componente ale impulsului perechii de particule considerate. Pentru ciocniri nucleare relativiste cele mai folosite perechi sunt cele de pioni, kaoni si protoni. În cele mai multe situatii de interes, analiza se face in sistemul de coordnate "exterior" ("long-side-out"; se considera ca "long" este directia impulsului, "out" este directia impulsului transversal al perechii de pioni, "side" este planul perpendicular pe directia "out"). Sistemul "exterior" este prezentat in Fig.II.3. Asupra unor aspecte legate de alegerea sistemului de coordonate se va mai reveni in curs.
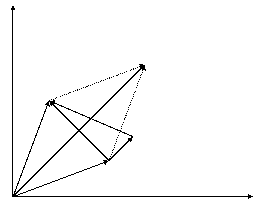
y
pt=pt1+pt2
pt1 qside
q
qout
pt2
x
Fig.II.3. Sistemul de coordonate "exterior"
Pentru deducerea razelor efective ale sursei cu luarea in considerare a contributiei curgerii la functia de corelatie se introduce o functie de corelatie de urmatoarea forma:
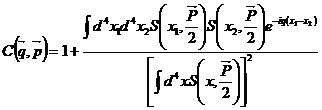 , (II.90)
, (II.90)
unde ![]() este functia
sursei, q = p1-p2
este 4-impulsul relativ si P=p1+p2
este 4-impulsul total al perechii;
este functia
sursei, q = p1-p2
este 4-impulsul relativ si P=p1+p2
este 4-impulsul total al perechii; ![]() , p1
si p2 sint
4-impulsurile particuleor considerate (in cele mai multe cazuri, pioni).
Considerind forma exacta a functiei de corelatie, se pot
genera corectiile datorate geometriei sursei. Se foloseste
functia de corelatie din relatia (II.90). Pentru considerarea
corelatiei spatiu-impuls se presupune ca functia sursei nu
este factorizata, adica:
, p1
si p2 sint
4-impulsurile particuleor considerate (in cele mai multe cazuri, pioni).
Considerind forma exacta a functiei de corelatie, se pot
genera corectiile datorate geometriei sursei. Se foloseste
functia de corelatie din relatia (II.90). Pentru considerarea
corelatiei spatiu-impuls se presupune ca functia sursei nu
este factorizata, adica:
![]() . (II.91)
. (II.91)
Marimea sursei masurate nu este marimea intregii surse, ci doar regiunea efectiva care emite particulele identice proprii considerate (se da lungimea omogenitatii).
Pentru efectuarea calculelor necesare in forma covarianta, in unele modele, se introduce 4-viteza sursei . În general, insa, se urmareste obtinerea unor relatii de calcul independente de model. De aceea, in cele mai multe cazuri de interes se lucreaza cu transformari Lorentz intre sisteme de referinta diferite. Scopul principal este stabilirea relatiilor dintre marimea sursei si functia de corelatie Hanbury-Brown - Twiss, functie masurata atunci cind sursa este in miscare.
Functia de corelatie este prin definitie raportul dintre densitatea invarianta biparticula si produsul densitatilor invariante uniparticula.
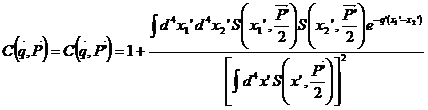 , (II.92)
, (II.92)
unde prin prim (') s-au notat valorile coordonatelelor si ale impulsului in acest sistem [82-84].
În cadrul modelului termodinamic de "sfera fierbinte" (fireball), la fiecare parametru de ciocnire partile care se suprapun ale nucleului proiectil si ale nucleului tinta se amesteca si toata energia este convertita intr-o miscare aleatoare. O astfel de conversie poate avea loc daca "sfera fierbinte" (fireball-ul) pierde memoria modului in care a fost creat.
Fie cazul in care numarul de particule nu este mare, in ipoteza ca in "sfera fierbinte" nu exista decat nucleoni, avand masa de repaus m si pioni cu masa de repaus mπ. Probabilitatea de a avea n1 protoni, n2 neutroni, n3 pioni pozitivi, n4 pioni negativi si n5 pioni neutri este data de o relatie de forma:
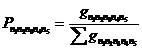 . (II.93)
. (II.93)
unde
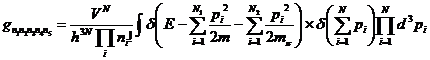 , (II.94)
, (II.94)
cu
N1=n1+n2 , (II.94a)
N2=n3+n4+n5 , (II.94b)
N=N1+N2 , (II.94c)
E=Erel-N1mc2-N2mπc2 . (II.94d)
Multiplicitatile n1, n2, n3, n4, n5 trebuie sa respecte legile conservarii numarului barionic si sarcinii, anume:
n1+n3-n4=Q , (II.95a)
n1+n2=B . (II.95b)
Ecuatia (II.94) este o aproximatie nerelativista. Ea poate fi aplicata pentru ciocniri de ioni cu numere de masa egale si energii in sistemul laboratorului de cel mult 800 MeV/nucleon, ceea ce corespunde la 182 MeV/nucleon in sistemul centrului de masa. Trebuie mentionat faptul ca, pentru astfel de ciocniri, aproximatia nerelativista este corecta pentru nucleoni. Este mai putin corecta pentru pioni, care au o masa de repaus mult mai mica. Integrala din ecuatia (II.94) poate fi evaluata formal. Generalizarea relativista a ecuatiei (II.94) nu poate fi evaluata pentru un numar mare de particule.
Pentru un parametru de ciocnire dat, spectrul inclusiv pentru pioni negativi pentru un impuls relativ p, in sistemul de coordonate atasat "sferei fierbinti", in repaus, este dat de relatia de mai jos:
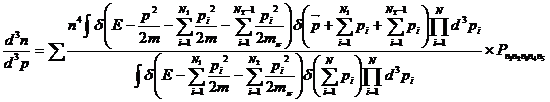
(II.96)
Fie
cazul a doi protoni in sistemul de coordonate in repaus atasat
"sferei fierbinti" (fireball-ului). Se face ipoteza ca in
"sfera fierbinte" (fireball) se afla np
protoni si nn
neutroni (cu np+nn=n),
cu energia nerelativista E. Se
considera un experiment in care un proton care se misca pe
directia x cu un impuls fixat ![]() este masurat
in coincidenta cu un alt proton care se misca pe
directia opusa (directie aflata la 180o
fata de prima), dar avind orice marime
este masurat
in coincidenta cu un alt proton care se misca pe
directia opusa (directie aflata la 180o
fata de prima), dar avind orice marime ![]() . Consideram si o alta configuratie
in care se masoara protoni cu un impuls fixat
. Consideram si o alta configuratie
in care se masoara protoni cu un impuls fixat ![]() pe axa x, dar al doilea este pe directia y (deci, la 90o
fata de primul). Definim raportul acestor doua numere ca pe o corelatie:
pe axa x, dar al doilea este pe directia y (deci, la 90o
fata de primul). Definim raportul acestor doua numere ca pe o corelatie:
![]() . (II.97)
. (II.97)
În acest raport, numaratorul si numitorul, sunt dati de urmatoarea relatie:
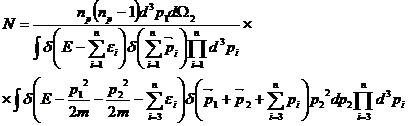 . (II.98)
. (II.98)
Pentru prima configuratie, ![]() este in
directia data de unghiul de 180o, iar pentru cea de a doua configuratie directia este cea
data de unghiul de 90o.
este in
directia data de unghiul de 180o, iar pentru cea de a doua configuratie directia este cea
data de unghiul de 90o.
Dupa sumarea pe parametrii de ciocnire, corelatia data de ecuatia (II.97) se poate scrie astfel
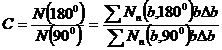 . (II.99)
. (II.99)
Luand in considerare spinii particulelor emise si detectate (fermioni sau bozoni) se pot scrie relatii specifice.
În ipoteza ca functiile de
unda ale bozonilor pot fi descrise prin functii de unda plane,
amplitudinea de detectie a doi bozoni identici de la o sursa cu
emisie spatio-temporala punctuala, fiecare avand
pozitiile si impulsurile (![]() ), respectiv, (
), respectiv, (![]() ), se poate scrie in forma urmatoare:
), se poate scrie in forma urmatoare:
![]() , (II.100)
, (II.100)
unde ![]() , respectiv,
, respectiv, ![]() sunt punctele
detectiei pentru particulele de impulsuri
sunt punctele
detectiei pentru particulele de impulsuri ![]() si, respectiv,
si, respectiv, ![]() . Probabilitatea de
detectie a unei perechi de bozoni este data de integrala
patratului amplitudinii, anume:
. Probabilitatea de
detectie a unei perechi de bozoni este data de integrala
patratului amplitudinii, anume:
![]() , (II.101)
, (II.101)
unde ![]() este distributia
spatio-temporala a bozonilor in sursa. Integrarea se face
pe toata distributia bozonilor in sursa. Daca
distributiile spatio-temporale sint independente de impuls,
integrala se separa si se reduce la:
este distributia
spatio-temporala a bozonilor in sursa. Integrarea se face
pe toata distributia bozonilor in sursa. Daca
distributiile spatio-temporale sint independente de impuls,
integrala se separa si se reduce la:
![]() , (II.102)
, (II.102)
unde ![]() este 4-impulsul
este 4-impulsul ![]() si C2ideal este functia de corelatie.
si C2ideal este functia de corelatie.
Aceasta este interpretarea "traditionala" a functiei de corelatie. Ea permite determinarea caracteristicilor spatio-temporale ale sursei de particule.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |