
Energia electromagnetica a unei distributii volumice de sarcina si de curent in vid
Se considera o distributie
volumica de sarcina in vid caracterizata de vectorul densitate
volumica de curent ![]() , unde
, unde ![]() este viteza de
deplasare a elementrului de sarcina mobila
este viteza de
deplasare a elementrului de sarcina mobila ![]() . Acest element este supus actiunii fortei Lorentz
. Acest element este supus actiunii fortei Lorentz ![]() . Cum forta magnetica nu produce lucru mecanic,
puterea primita de elementul de sarcina mobila din partea
campului electromagnetic este :
. Cum forta magnetica nu produce lucru mecanic,
puterea primita de elementul de sarcina mobila din partea
campului electromagnetic este :
![]()
Integrand pe volumul V, se obtine puterea primita de ansamblul sarcinilor :
![]() (1)
(1)
Folosind ecuatia Maxwell -
Ampère 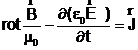 , se obtine :
, se obtine :
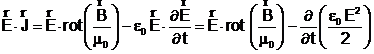 (2)
(2)
Din analiza matematica este cunoscuta relatia :
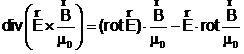
si cum
![]()
relatia (2) devine
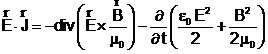
Prin integrarea relatiei precedente se obtine ecuatia
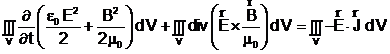
si prin permutarea operatorilor de integrare si derivare :
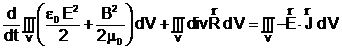 (3)
(3)
unde
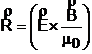 (4)
(4)
este vectorul Poynting. Relatia (3) este cunoscuta sub numele de teorema Poynting.
Folosind formula Gauss Ostrogradski aplicata suprafetei S ce delimiteaza volumul V, ecuatia (3) se pune sub forma :
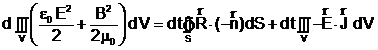 (5)
(5)
Aceasta noua forma a teoremei Poynting conduce la o interpretare energetica in termeni de bilant pentru marimea
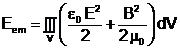 (6)
(6)
numita energie electromagnetica.
Energia electromagnetica se reduce la o forma pur electrica :
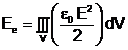 (7)
(7)
atunci
cand ![]() . Deci, in regim stationar regasim energia
electrostatica. Prin analogie se defineste energia
magnetica :
. Deci, in regim stationar regasim energia
electrostatica. Prin analogie se defineste energia
magnetica :
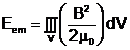 (8)
(8)
obtinuta prin anularea campului electric.
In regim variabil, ![]() fiind cuplati,
energia electromagnetica este suma a doi termeni inseparabili, unul de
natura electrica, de densitate volumica
fiind cuplati,
energia electromagnetica este suma a doi termeni inseparabili, unul de
natura electrica, de densitate volumica ![]() si unul de
natura magnetica, de densitate volumica
si unul de
natura magnetica, de densitate volumica ![]() .
.
Ecuatia de bilant pentru energia electromagnetica poate fi pusa sub forma unei ecuatii de bilant pentru o marime extensiva :
![]() (9)
(9)
Deci variatia energiei electromagnetice elementare comporta doi termeni : primul se scrie :
![]() (10)
(10)
ce
reprezinta energia primita (algebric) de la mediul exterior.
Aceasta energie arata ca vectorul Poynting ![]() poate fi interpretat
ca o densitate volumica de energie electromagnetica.
poate fi interpretat
ca o densitate volumica de energie electromagnetica.
Al doilea termen :
![]() (11)
(11)
traduce neconservarea energiei electromagnetice si deci existenta unei surse de productie a acestei energii.
In absenta surselor ![]() , teorema Poynting se scrie local :
, teorema Poynting se scrie local :
![]()
unde
![]()
este energia electromagnetica volumica, si
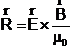
este vectorul Poynting.
In cazul in care termenul de
productie ![]() este nul, energia
electromagnetica se conserva. Integrand relatia locala
pentru volumul V fix se obtine :
este nul, energia
electromagnetica se conserva. Integrand relatia locala
pentru volumul V fix se obtine :
![]()
Relatia precedenta traduce un bilant intre energia electromagnetica continuta in volumul V :
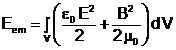
si puterea radiata prin suprafata S ce delimiteaza volumul V :
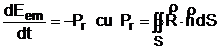
deci, in vid si in absenta sarcinilor, variatia energiei electromagnetice se traduce prin existenta radiatiei.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |