Erori alias
Aspectul dreptelor si curbelor pe ecrane cu rezolutie slaba poate fi considerat inestetic, fiind perceptibila reprezentarea prin puncte distincte. Liniile au un aspect rugos, grosimea este neuniforma. In contextul teoretic al prelucrarii semnalelor, problema poate fi identificata ca una de subesantionare. Aici vom face doar o scurta discutie, mai degraba pragmatica si intuitiva asupra modalitatilor de abordare posibile. Mentionam doar ca termenul alias desemneaza in limba engleza un nume echivalent. Asemeni spionilor ce-si ascund identitatea reala sub un alias, componente de frecvente inalte din spectrul semnalului pot reapare cu frecventele modificate, determinand false componente de joasa frecventa si de aici imposibilitatea reconstruirii corecte a semnalului, la o esantionare insuficient de fina.
O prima solutie posibila consta in cresterea rezolutiei. Este o solutie costisitoare in sensul consumului de memorie si cresterii timpului de trasare. In plus, nu rezolva problema de fond, o face doar mai putin acuta.
O solutie alternativa consta filtrarea imaginilor prin convolutie cu un operator de tip trece jos (filtru de netezire). Asemenea filtre se vor prezenta intr-un capitol special dedicat. Filtrarea transforma imaginea binara (cu numai doua niveluri de gri, corespunzatorare albului si negrului) intr-o imagine cu nuante de gri.
O solutie a carei idee este foarte simpla, o reprezinta esantionarea de suprafata neponderata, ilustrata in figura.
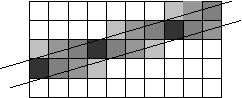
Intensitatea fiecarui pixel este proportionala cu procentul din suprafata sa ce se suprapune cu linia, considerata a avea o grosime finita, precizata. Prin intensitate intelegem in contextul de fata negativul ei. Astfel, intensitatii maxime, 255 ii corespunde negrul, 0. Valorii 100 ii corespunde 255 - 100 etc. Se obtine o redare cu tranzitii mai line a contururilor, cu un aspect mai natural, desi aparent metoda antreneaza o pierdere de rezolutie prin ingrosarea de facto a traseului liniei. O redare si mai realista a liniilor se obtine prin esantionare de suprafata ponderata. Metoda reprezinta o generalizere a ideii precedente, prin care intensitatea unui pixel depinde nu numai de procentul din aria sa suprapus cu traseul liniei ci si de distanta la mediana liniei. O interpretare posibila a esantionarii neponderate ar fi urmatoarea. Pe fiecare pixel suprapunem centrat un cub cu latura egala cu cea a pixelului. Daca linia intersecteaza pixelul, delimiteaza un subvolum al cubului (proportional cu suprafata de intersectie). Intensitatea pixelului este apoi stabilita proportionala cu subvolumul delimitat de linia ce se traseaza. La esantionarea de suprafata ponderata, figura centrata pe pixel nu mai este un cub. Poate fi inlocuita de exemplu cu un con, a carui inaltime descreste monoton de la centru spre margini, dar se poate utiliza orice alt corp cu proprietati similare (sfera, clopot gaussian etc.). Corpurile (ce stabilesc pana la urma dimensiunea pixelului) pot depasi in dimensiuni pasul retelei, ceea ce inseamna o suprapunere a zonelor acoperite de pixeli vecini. Nimic nou in acest aranjament, tinand cont de faptul ca acest lucru se intampla curent la toate monitoarele bazate pe tuburi catodice, la care spotul de explorare are o alura aproximativ gaussiana si acopera semnificativ mai mult decat o linie de explorare.
Tehnicile anti alias sunt incorporate uzual direct in algoritmii de trasare.
Transformari geometrice
Transforrmarile geometrice sunt folosite extensiv de programele de grafica pe calculator. Un program CAD pentru arhitecura, de exemplu, va folosi transformarea de translatie pentru a pozitiona cladirile si copacii la locul potrivit, rotatia pentru a le expune din unghiul dorit de utilizator si scalarea pentru a le reda la marimea la care se vad din pozitia specificata de utilizator.
1. Transformari 2D
Putem translata un punct de coordonate (x,y) la locatia dorita, (x*,y*), adunand diferentele coordonatelor la cele initiale:
|
|
(7.1) |
Definind vectorii coloana
|
|
(7.2) |
Ecuatia (7.1) poate fi rescrisa mai concis:
|
|
(7.3) |
Un punct poate fi rescalat de-a lungul axelor prin multiplicarea coordonatelor cu coeficientii adecvati:
|
|
(7.4) |
Notand
|
|
(7.5) |
Putem rescrie concis ecuatia (7.4) in forma
|
|
(7.6) |
De observat ca, in timp ce translatia nu afecteaza scara de redare, rescalarea afecteaza pozitia unui obiect pe ecran. De exemplu, avand triunghiul definit prin varfurile de coordonate (1,1), (2,4) si (3,1), centrul de greutate este la ((1+2+3)/3,(1+4+1)/3) = (2,2). Dupa rescalarea cu factorul sx=2 si sy=2, coordonatele noi vor fi (2,2), (4,8), (6,2) si centrul de greutate (4,4).
Rotatia cu ungiul α in sens trigonometric este descris de ecuatiile:
|
|
(7.7) |
In forma matriciala,
|
|
(7.8) |
2. Coordonate omogene si reprezentari matriciale ale transformarilor 2D
Reprezentarile matriciale introduse prezinta inconvenientul ca translatia este descrisa de o ecuatie cu forma diferita de cele pentru scalare sau rotatie. Acest neajuns poate fi inlaturat simplu prin introducerea coordonatelor omogene. Coordonatele omogene 2D ale unui punct sunt de forma unui triplet (xh, yh, w). Variabila suplimentara nu este propriu-zis o coordonata, desi se poate gasi si o interpretare de acest tip. Rolul ei este de a permite manipularea convenabila a calculelor cu transformari geometrice in forma matriciala. Coordonatele carteziene se obtin pe baza coordonatelor omogene prin ecuatiile:
|
|
(7.9) |
Frecvent se alege w=1, impartirea fiind astfel evitata, dar exista situatii in care este util ca w sa poata lua valori diferite de 1.
In coordonate omogene, translatia se poate scrie in forma:
|
|
(7.10) |
Mentionam ca unii autori prefera sa scrie ecuatia de mai sus cu vectorul linie al coordonatelor premultiplicand matricea de transformare, in speta matricea de translatie. In acest caz matricea de translatie are forma transpusa, pentru ca (Tp)T = pT TT.
In coordonate omogene toate cele trei transformari introduse au forma generala a ecuatiei (7.10). Ceea ce difera este numai forma matricii din ecuatia de tranformare. Pentru scalare, ecuatia ia forma:
|
|
(7.11) |
Respectiv pentru rotatie forma
|
|
(7.12) |
Ce se intampla daca facem doua translatii succesive cu (dx1, dy1) si (dx2, dy2)? Din proprietatile elementare ale operatiilor cu vectori, anticipam ca rezultatul este echivalent cu o translatie unica cu vectorul-suma (dx1+ dx2, dy1+ dy2). Este usor de verificat ca:
|
|
(7.13) |
Similar se comporta si celelalte doua transformari. Ele pot fi simplu concatenate, prin multiplicari succesive ale matricilor de transformare. Mai mult, o succesiune de transformari de tipul translatie, urmata de rescalare, urmata de a doua translatie, urmata de o rotatie, se poate realiza prin multiplicare cu o singura matrice M = RT2ST1.
Un exemplu de folosire a proprietatii de concatenare a transformarilor consta in rotatia unei figuri in jurul unui punct arbitrar, P, nesituat in originea sistemului de coordonate. Transformarea se poate realiza prin succesiunea:
1. Translatie ce aduce P in origine
2. Rotatie
3. Translatie ce readuce P la coordonatele initiale
Daca P are coordonatele (x,y) si unghiul de rotatie este α, succesiunea de transformari necesare are matricea de transformare
|
|
(7.14) |
O abordare similara este posibila pentru rescalarea unui obiect in jurul unui punct oarecare, de exemplu in jurul centrului de greutate al obiectului. Succesiunea de transformari este: translatie, scalare, retranslatie.
Este interesant de remarcat faptul ca operatiile de translatie comuta. La fel si cele de scalare sau rotatie. Mai mult, scalarea cu factor egal pe directiile x si y comuta cu rotatia. Matricile implicate sunt comutative. In general insa, inmultirea matricilor este numai asociativa, nu si comutativa.
3. Transformari geometrice 3D
Transformarile geometrice 3D pot fi exprimate avantajos folosind coordonate omogene 3D. Acestea se obtin adaugind vectorilor 2D o componenta suplimentara, corespunzatoare coordonatei z. Matricile de transformare devin matrici 4×4.
Exista doua sisteme de coordonate carteziene 3D, denumite de mana stanga si respectiv de mana dreapta. In cele ce urmeaza, vom folosi sistemul de mana dreapta.

In spatiul 3D, rotatiile sunt mai complexe decat in spatiul 2D. Rotatia 3D are loc in jurul unei axe. Pentru sistemul de mana dreapta, prin conventie, sensul de rotatie pozitiv este cel trigonometric, privind dinspre axa de rotatie spre origine. O rotatie pozitiva de 90o transforma una din axe in cealalta axa, in planul de rotatie.
Translatie 3D se poate scrie in forma:
|
|
(7.15) |
Scalarea 3D are forma:
|
|
(7.16) |
Matricea de rotatie in jurul axei z (in planul x-y) are forma:
|
|
(7.17) |
Matricea de rotatie pentru axa x este:
|
|
(7.18) |
Matricea de transformare pentru rotatie in jurul axei y este:
|
|
(7.19) |
Ultimele doua se pot obtine din prima prin permutari circulare succesive in submatricea 3×3 din stanga sus.
Rotatia in jurul unei axe oarecare, definita de doua puncte P1, P2, cu un unghi α se poate realiza, de exemplu, in urmatorii pasi:
translatie ce aduce P1 in originea sistemului de coordonate
rotatie ce aduce P2 in planul xOz
rotatie in jurul axei y, ce aduce P2 pe axa z
rotatia dorita cu unghiul α, in jurul axei z
rotatie in jurul axei y, pentru inversarea efectului rotatiei de la punctul 3
rotatie in jurul axei x, pentru inversarea efectului rotasiei de la punctul 2
translatie pentru a readuce P1 in pozitia initiala.
Matricea de transformare se poate scrie in forma:
|
M = TP1R-xR-yRzRyRxT-P1 |
(7.20) |
4. Proiectii
Redarea unui obiect grafic 3D pe ecran presupune o reprezentare 2D. Trecerea la reprezentarea 2D se poate realiza folosind o transformare de proiectie. In grafica de calculator se folosesc mai multe tipuri de proiectii. Exista doua categorii majore:
proiectii paralele
proiectia de perspectiva
O proiectie este definita de doua elemente geometrice:
planul de proiectie
punctul de proiectie
Punctele imaginii proiectate se obtin ca intersectii cu planul de proiectie ale unor segmente de dreapta ce unesc puncte ale obiectului cu punctul de proiectie.
Proiectiile paralele corespund reprezentarilor necesare in desenul tehnic ingineresc. In acest caz, punctul de proiectie este situat la infinit. Dreptele de proiectie sunt paralele intre ele si uzual paralele si cu una din axele sistemului. Proiectia de perspectiva corespunde vederii naturale si genereaza imagini cu aspect mai realist. Obiectele indepartate au dimensiuni micsorate in conformitate cu efectul de perspectiva. Paralelismul dreptelor si marimile unghiurilor nu se pastreaza, insa, ceea ce poate fi inconvenabil pentru reprezentarile ingineresti.
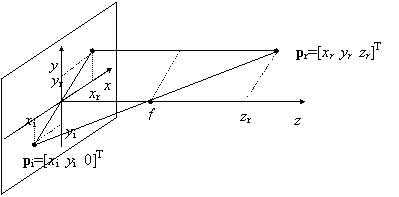
Din punct de vedere practic, este mai simplu aranjamentul in care planul de proiectie coincide cu unul din planurile determinate de o pereche de axe de coordonate. Uzual, este planul xOy. Proiectia unui punct din lumea reala pe planul xOy este ilustrata in figura de mai jos.
![]() (7.21)
(7.21)
de unde rezulta imediat ca
![]() (7.22)
(7.22)
Similar, se gaseste si pentru axa y ca
![]() (7.23)
(7.23)
Ecuatiile transformarii de perspectiva, deduse mai sus, ne permit calculul coordonatelor punctului din planul imagine in functie de coordonatele punctului din lumea reala care l-a generat. Pe de alta parte, zi=0, independent de coordonatele punctului din lumea reala. Din acest motiv, operatia inversa, de reconstituire a coordonatelor punctului din lumea reala in functie de coordonatele punctului din imagine devine imposibila. Constatarea nu este deloc surprinzatoare. Este clar ca toate punctele situate pe dreapta de proiectie ce uneste punctul proiectat cu imaginea sa si trece prin centrul optic se proiecteaza la aceleasi coordonate din planul imagine. Ecuatiile (7.21) si (7.22) definesc doua plane. Considerate ca un sistem, ele definesc intersectia celor doua plane care este chiar dreapta mentionata mai sus.
Aranjamentul din figura corespunde formarii imaginii pe camera de luat vederi. Parametrul f este centrul optic echivalent. Pentru grafica de calculator se considera adesea centrul de proiectie situat in spatele planului de proiectie si ecuatiile transformarii de perspectiva iau forma:
|
|
(7.24) |
Ecuatiile de mai sus pot fi exprimate convenabil in forma matriciala, folosind coordonate omogene:
|
|
(7.25) |
Pe baza coordonatelor omogene, folosind ecuatia (7.9), se pot obtine rapid coordonatele carteziene specificate de ecuatia (7.24). Verificarea este lasata in seama cititorului.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |