
CALCULUL PALETELOR DE COMPRESOR AXIAL SOLICITATE LA SOCURI MECANICE MARI.
1. Probleme generale.
Solicitarea prin soc a paletei se produce mai ales la primele trepte de compresor, si cel mai frecvent la prima treapta de compresor axial sau ventilator, sub actiunea corpurilor straine care patrund in motor.
Aceste corpuri straine pot avea dimensiuni si naturi diferite (pamant, pietre, pasari, corpuri metalice), si corespunzator pot provoca suprasolicitari locale, deformatii locale ale aerofoliei, ciupituri pe bordul de atac, ruperi locale sau fisurari, ruperi de palete, precum si afectarea treptelor urmatoare si a curgerii prin compresor. Efectele patrunderii corpurilor straine vor fi influentate, in afara de particularitatile mecanice si dinamice ale corpului strain care patrunde in motor, si de constructia retelei de palete. Practic intereseaza doua solutii de realizare a treptei de compresor:
trepta de compresor axial avand o retea de aparat director in fata,
- treapta de compresor axial fara
aparat director, la care corpurile straine lovesc
direct reteaua de palete de rotor.
In primul caz, solicitarea prin soc este suportata mai ales de reteaua de palete de stator, care obisnuit are paletele incastrate la ambele capete.
In cel de al doilea caz, socul se manifesta direct asupra paletelor de rotor, care, in cazul treptelor de ventilator, aceste palete au lungimi foarte mari, sunt mult torsionate si foarte flexibile, se rotesc cu viteze unghiulare mari, iar viteza pe directie axiala a aerului prin retea poate avea de asemenea viteze deosebite. Toate acestea vor determina si aparitia unor efecte foarte periculoase pentru starea functionala a paletei, care pot duce la distrugerea motorului si producerea de catastrofe cand patrunderea corpurilor straine are loc pe timpul evolutiilor de zbor ale aeronavei echipata cu motorul respectiv. Solicitarea prin soc determina asupra paletei, aparitia unor tensiuni locale foarte mari, precum si tensiuni suplimentare in restul sectiunilor aerofoliei produse de forta de impact aplicata pe o lungime relativ mica a bordului de atac al aerofoliei, soc ce se va propaga in toata masa paletei. Are loc si un proces de excitare la vibratie, constituind o sursa de crestere a tensiunilor totale prin efectul tensiunilor produse de vibratii, precum si de initiere a unor curgeri instabile prin retea si prin intregul compresor (pompaj). Luand in considerare si dispunerea profilelor paletelor in retea, ca si directiile pe care se poate deplasa corpul strain, respectiv locul de impact pe paleta, procesul se poate complica si mai mult, la aceasta influentand si sensurile de miscare, pe directie axiala pentru corpul strain, si pe directie tangentiala pentru reteaua de palete. Tinand seama de complexitatea fenomenului, calculul tensiunilor si a deformatiilor din aerofolie solicitate si la soc poate fi efectuat numai in limitele unor particularizari si a unor ipoteze de calcul cat mai apropiate de situatiile reale. Ca particularizari admitem sa se efectueze calculul pentru cazurile:
- palete de aparat director,
- palete de rotor compresor.
Pentru stabilirea relatiilor de calcul se fac urmatoarele ipoteze generale:
-paleta supusa socului se comporta perfect elastic, ca si in cazul solicitarilor fara soc.
corpul strain care
loveste ramane dupa lovire, in contact cu paleta, respectiv
se considera ca transfera
acesteia intreaga energie cinetica a corpului care a lovit.
nu se considera efectul deformatiilor locale in timpul socului, respectiv nu se apreciaza energia disipata prin deformatiile plastice locale.
transmiterea deformatiilor in intreaga masa a paletei se face in acelasi timp cu socul,
Aceste ipoteze permit ca, in prima aproximatie, efectul
socului sa fie asimilat cu acela al multiplicarii
sarcinei statice pe paleta, cu un coeficient dinamic ![]() care se determina
in conditiile neglijarii masei paletei, sau cu considerarea acestei
mase.
care se determina
in conditiile neglijarii masei paletei, sau cu considerarea acestei
mase.
2. Calculul
coeficientului dinamic ![]() .
.
Se determina coeficientul dinamic facand ipotezele:
paleta este solicitata prin soc la incovoiere,
sub actiunea fortei dinamice Pd, se produce o sageata dinamica yd,
intreaga energie cinetica a greutatii corpului strain este cedata paletei ca energie de deformatie, transformandu-se in energie potentiala.
Daca se noteaza:
P - sarcina statica,
Pd - sarcina dinamica,
K - constanta elastica a barei,
ys - sageata statica,
yd - sageata dinamica
rezulta
![]() (1)
(1)
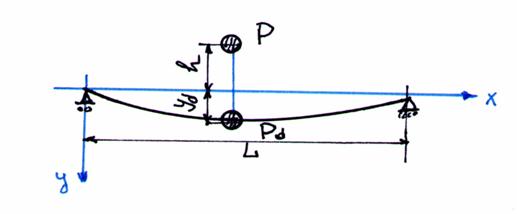
Fig. 31
Relatiile dintre sageti si sarcini sunt:
![]()
![]() (2)
(2)
Valorile constantelor K, pentru diferitele conditii de fixare a paletei in retea se pot obtine din tabelul urmator, in care s-a notat:
E - modulul de elasticitate al materialului barei,
Jd - momentul de inertie diametral fata de axa de incovoiere considerata,
L - lungimea barei.
|
Bara incastrata la un capat si libera la celalalt capat. Masa este concentrata la capatul liber al barei. |
|
|
Bara simplu rezemata. Masa este concentrata intr-o sectiune oarecare a barei. (a ≠ b). Daca masa este concentrata la mijlocul barei a = b = |
|
|
Bara incastrata la ambele capete cu masa dispusa intr-o sectiune oarecare, (a ≠ b). Daca masa este concentrata la mijlocul barei, (a = b) |
|
Din relatiile (1), (2) rezulta,
![]()
sau
![]()
Si radacina pozitiva va fi ,
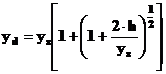
Daca se noteaza,
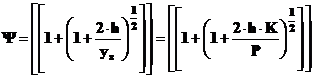
![]()
atunci
![]() ,
,
in care
h - inaltimea de cadere a sarcinei, P.
ys - sageata in dreptul sarcinei P, considerand ca sarcina este aplicata static asupra barei (paletei).
Daca foita P se aplica brusc, cu intreaga
intensitate, fara viteza initiala (h = 0), coeficientul
dinamic ![]() = 2 .
= 2 .
Daca in loc de inaltimea h, se da sarcinei P o viteza de lovire, stiind ca viteza este
![]()
g - acceleratia gravitatiei.
Expresia coeficientului dinamic va fi
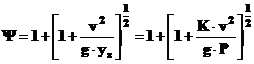
Tensiunile dinamice in cazul incovoierii paletei prin soc se obtin din,
![]() ,
,
in care
ad - tensiunile de incovoiere in conditiile de soc,
M - momentul incovoietor in conditii statice, fara soc,
Wd - modulul de rezistenta diametral al paletei fata de axa dupa care se produce deformatia.
Daca paleta este simplu rezemata, iar sarcina actioneaza la mijlocul ei, admitand ca h ≥ 100∙ys, se poate considera coeficientul dinamic ca fiind
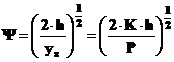
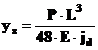
tensiunile fiind
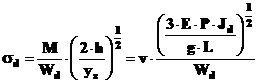
in cazul paletelor P este greutatea corpului strain G, P = G, si dupa ridicare la patrat se obtine,
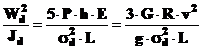
Daca se admite ca ![]() ,
, ![]() fiind tensiunea
admisibila, rezulta conditiile la care paleta poate functiona in conditii de soc.
fiind tensiunea
admisibila, rezulta conditiile la care paleta poate functiona in conditii de soc.
Coeficientul ![]() este cu atat mai mic
cu cat sageata statica este mai mare. Daca rigiditatea K este
mare, sageata statica ys, este foatre mica si se
poate produce distrugera pieselor, asa cum are loc la paletele
din materiale ceramice care sunt fragile si putin deformabile.
este cu atat mai mic
cu cat sageata statica este mai mare. Daca rigiditatea K este
mare, sageata statica ys, este foatre mica si se
poate produce distrugera pieselor, asa cum are loc la paletele
din materiale ceramice care sunt fragile si putin deformabile.
3. Considerarea masei paletei.
Cand se considera si masa paletei, coeficientul
dinamic ![]() , se calculeaza prin intermediul unui
coeficient subunitar C1, care depinde atat de masa paletei cat si
de masa corpului strain, respectiv,
, se calculeaza prin intermediul unui
coeficient subunitar C1, care depinde atat de masa paletei cat si
de masa corpului strain, respectiv,
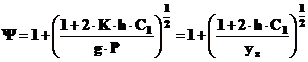
sau functie de viteza v, rezulta,
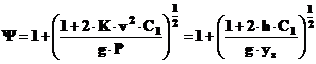
Valorile coeficientului C1 pentru bare drepte si pentru diferite moduri de rezemare sunt prezentate in tabelul nr.2.
In tabel,
G = P = m∙g - greutatea corpului care cade,
G1 = m1∙g - greutatea barei,
G2=m2∙g - greutatea unui corp cu masa concentrata fixata la bara (ex. bandajul paletei),
C - coeficient de corectie care poate avea valorile:
C = 1, C = C1, C = C2
4. Influenta socului asupra tensiunilor de torsiune din rotorul compresorului.
Se considera rotorul format din discuri si arbore. Arborele are diametrul d, iar rotorul (discurile) are diametrul D. Greutatea rotorului fiind G.
Energia cinetica a rotorului aflat in miscare de rotatie cu viteza unghiulara ω si a carui moment de inertie masic este Jm se obtine din,
![]()
dar ![]() ,
,
ns - turatia motorului (rot / sec).
Daca rotorul se considera ca fiind un disc avand diametrul D si greutatea Grot, momentul de inertie masic va fi,
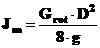
Energia de deformatie (lucrul mecanic) al arborelui, este
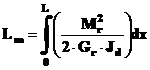
![]()
|
Schema |
Coeficientul |
CoeficC1 cand G1 =0, G2 = 0 |
Coeficientul C1 cand G1 ≠ 0, G2 = 0 |
Coeficientul C1 cand G1 ≠ 0, G2 ≠ 0 |
|
|
|
C1 = 1 |
|
|
|
|
|
C1 = 1 |
|
|
|
|
|
C1 = 1 |
|
|
in care
Mr - momentul de torsiune al arborelui,
Gr - modulul de elasticitate la torsiune al materialului arborelui,
![]()
E - modulul de elasticitate la incovoiere al materialului arborelui,
μ - coeficientul Poisson,
μ = 0,3 pentru domeniul elastic de deformatie
μ = 0,5 pentru domeniul plastic de deformatie
Jp - momentul de inertie polar al sectiunii arborelui,
![]()
Jd - momentul de inertie diametral al ariei sectiunii arborelui,
τmax - tensiunea de rasucire maxima.
Pentru arbore cu sectiune plina,
![]()
![]()
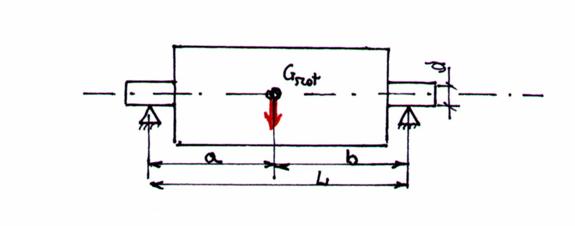
Fig. 32 - Schema rotorului.
Inlocuind Mr in Lm si considerand Mr = ct, Gr = ct, Jp = ct, d = ct, rezulta,
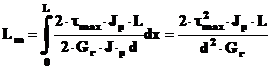
Egaland Ec = Lm,
rezulta,
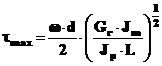
In cazul cand
![]() ,
, ![]()
Daca se noteaza volumul arborelui cu Va, si se considera lungimea b,
![]()
atunci
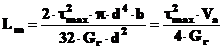
sau
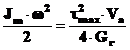 ,
,
iar
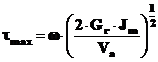
Considerand diametrul D si greutatea rotorului Grot, atunci momentul de inertie masic Jm,
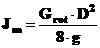 , iar
, iar ![]() ,
,
se obtine
![]()
sau
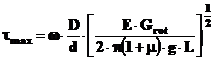
Daca se considera si masa arborelui, momentul Jm va fi,
![]() ,
,
Jma fiind momentul masic al arborelui,
![]()
5 Calculul la soc a paletei de aparat director sau a montantilor.
Treapta de aparat director reprezinta o retea de palete de stator, palete care sunt incastrate la ambele capete, si dispuse in fata primei trepte de rotor compresor.
Paletele sunt solicitate la incovoiere si torsiune sub actiunea presiunii aerului care trece catre rotorul compresorului, precum si la soc, atunci cand patrund in motor corpuri straine.
Calculul retelei de palete la soc este un calcul de verificare, deoarece dimensiunile geometrice ale retelei sunt definite, urmarindu-se fie stabilirea masei limita a corpului strain, avand anumite particularitati structurale si care a patruns in dispozitivul de admisie, astfel incat paleta sa reziste, fie alegerea materialului din care sa se execute paleta pentru ca aceasta sa functioneze sigur la socul de impact cu un corp strain de masa si constitutie data.
Similar cu paleta de stator se pot face verificari la soc si in cazul montantilor. Pentru calculul paletei de stator la soc, se fac ipotezele:
paleta are aria sectiunii constanta in lungul ei,
curentul de aer are parametrii uniformi la intrarea in reteaua de palete,
pentru a nu apare deformatii sau fisuri in
palete se considera ca tensiunea limita admisibila in
conditiile de soc este egala cu tensiunea
limita de curgere a materialului paletei, respectiv ac,
corpul strain actioneaza ca o forta concentrata pe paleta,
corpul strain are o viteza de deplasare
egala cu viteza aerului la intrarea
in retea,
impactul se produce la bordul de atac al profilului
paletei pe directia
vitezei relative
a aerului, deformatia paletei este mai ales de incovoiere, fata de axa minima de inertie η.
In limitele ipotezelor facute, paleta se prezinta ca o bara cu masa uniform distribuita, incastrata la ambele capete si, daca se accepta ca lovirea paletei se face la jumatatea lungimii, in acest caz coeficientul dinamic Ψ are expresia,
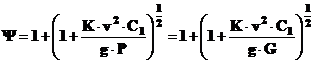
Pentru a = b,
valoarea ![]() ,
,
iar coeficientul C1 este,
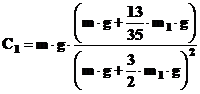
sau 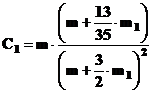 ,
,
in care s-au notat:
m - masa corpului strain care loveste paleta,
m1 - masa corpului paletei,
g - acceleratia gravitatiei.
dar
P = G = m∙g,
deci
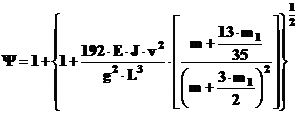
mai simplu,
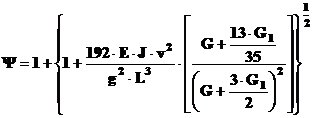
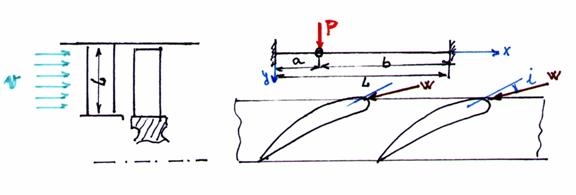
Fig. 33 - Schema de calcul.
Considerand expresia coeficientului de siguranta ca fiind,
![]() ,
,
unde
![]() - tensiunea admisibila, de durata si
considerand conditiile de lucru al materialului paletei,
- tensiunea admisibila, de durata si
considerand conditiile de lucru al materialului paletei,
![]() - tensiunile rezultante in
paleta,
- tensiunile rezultante in
paleta,
![]() - tensiunile de incovoiere date de presiunea gazelor,
- tensiunile de incovoiere date de presiunea gazelor,
![]() - tensiuni de incovoiere produse de soc,
- tensiuni de incovoiere produse de soc,
![]() - tensiuni din vibratii,
- tensiuni din vibratii,
![]() - tensiuni termice.
- tensiuni termice.
Pentru paleta de aparat director la care temperatura este mica, iar paleta este foarte rigida, se vor considera,
![]() ,
,![]() ,
,
ca urmare,
![]()
Deoarece materialul paletei si resursa sunt
marimi impuse, iar prin ipoteza se admite ca fiind cunoscuta si limita de
curgere, rezulta ca se considera coeficientul de siguranta
ca avand valoarea n = 1. De asemenea se cunoaste momentul incovoietor dat de
forta de presiune a aerului, respectiv
![]() .
.
Ca urmare,
![]()
sau
![]()
dar,
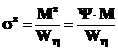
Ms - momentul incovoietor produs de soc,
Wη - modulul de rezistenta la incovoiere a paletei fata de axa minima de inertie,
M - momentul incovoietor dezvoltat daca forta produsa de corpil strain ar actiona static.
Inlocuind, rezulta,
![]()
deci,
![]()
Dar pentru bara incastrata la ambele capete, avand sarcina actionand la mijlocul ei,
![]()
Deoarece P = G, rezulta:
![]() ,
,
sau inlocuind G, L in expresia lui Ψ, se obtine:
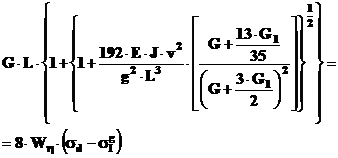
Euatie care se va rezolva iterativ obtinandu-se valoarea greutatii G,
G = m∙g
respectiv masa corpului strain care poate lovi paleta cand coeficientul de siguranta
n = l ![]()
Dar paletele de aparat director (stator) sunt profilate si au parametrii geometrici urmatori:
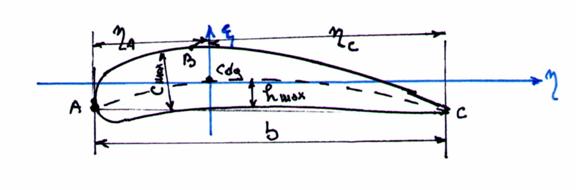
Fig. 34 - Parametrii profilului.
Se poate admite la aceste palete ca fiind indeplinite urmatoarele ipoteze:
- aria sectiunii paletei este constanta in lungul paletei si rezultand din.
A = 0,7 ∙ b ∙ cmax
- momentele de inertie fata de axele principale sunt:
Jη = 0,041∙b∙cmax∙(![]() +
+![]() )
)
Jξ = 0,038∙b3∙cmax
- paletele sunt dispuse inclinat in retea,
- paletele nu sunt torsionate,
- temperatura paletelor este constanta,
- corpul strain loveste paleta pe directia vitezei relative a aerului, care are unghiul de incidenta fata de directia de curgere axiala.
-paleta este solicitata la
incovoiere si torsiune sub actiunea fortelor de
presiune a aerului si a celor produse
din socul dat de corpul strain care loveste paleta, sub forma
concentrata.
- modulul de rezistenta, in punctul A si respectiv C al profilului paletei,
![]()
![]()
- greutatea
paletei avand aria sectiunii
![]() ,
,
ρ - densitatea materialului paletei.
Punctul cel mai solicitat pe profil este C, unde modulul de rezistenta este cel mai mic. Ca urmare, relatia de calcul in cazul paletei de stator (montantilor) va fi :
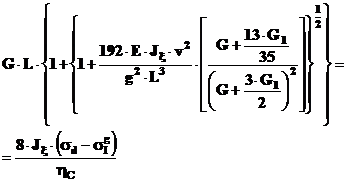
6. Calculul paletei de rotor compresor axial treapta I
Particularitatile constructive ale paletelor de rotor compresor axial sunt:
- paleta are parametrii geometrici variind in lungul razei,
- paleta se poate asimila cu o bara sau o placa incastrata la un capat si libera la celalalt capat,
- paleta poate avea elemente de rigidizare dispuse pe corpul ei,
- torsionarea corpului paletei pate fi neglijabila, sau foarte mare,
- reteaua de palete este in miscare de rotatie,
- viteza axiala de patrundere a aerului in retea este determinata de conditiile de lucru ale motorului, dar si de regimul de zbor.
Pentru calculul efectelor patrunderii corpurilor straine in reteaua de compresor (ventilator), se fac urmatoarele ipoteze:
- reteaua de palete nu are in fata aparat director sau montanti, care ar putea anihila patrunderea corpului strain,
- corpul strain are la intrarea in retea viteza axiala a curentului de aer si loveste paleta catre partea bordului de atac cu o viteza corespunzatoare vitezei relative, prin care se considera si efectuctul antrenarii in rotatie a paletei,
- se vor considera solicitarile cele mai mari din paleta care se produc atunci cand corpul strain loveste paleta catre varful acesteia, se presupun ca fiind cunoscute dimensiunile paletei, materialul din care este executata, turatiile de lucru ale motorului, distributiile de presiuni pe aerofolie, vitezele de curgere ale aerului si sunt calculate tensiunile de intindere, incovoiere, torsiune, vibratii, pentru paleta lucrand in conditii normale,
- efectele patrunderii corpului strain si impactul cu corpul paletei determina aparitia unor tensiuni suplimentare, care se vor insuma cu cele existente in paleta in momentul ciocnirii,
- la calculul tensiunilor totale, se vor neglija influenta tensiunilor termice, deoarece acestea, ca si resursa paletei, se vor aprecia prin valoarea tensiunii la limita de curgere, considerata la calculul coeficientului de siguranta,
- la paletele torsionate se considera ca unghiul de torsiune este nul in sectiunea de la baza aerofoliei, iar centrele de greutate ale sectiunilor succesive ale paletei sunt situate pe raza care trece prin centrul de greutate al sectiunii de la baza aerofoliei,
- corpul paletei torsionate are latimea constanta a treptei, dar corzile profilelor cresc de la baza catre varful paletei,
- lungimea aerofoliei la partea bordului de atac, este mai mare fata de lungimea de la bordurile de fuga. Ca urmare, se va considera ca sectiunea de baza a aerofoliei va fi aceea corespunzand sectiunii complete a paletei care este perpendiculara pe raza centrelor de greutate ale profilelor,
- solicitarile se vor calcula in punctele A, B, C, caracteristice profilelor aerofoliei,
- axele necesare in calcul sunt notate astfel;
a - axa pe directia axiala de curgere a aerului, avand sensul catre aval,
u - axa vitezei periferice, dispusa in planul retelei. Pentru paleta de compresor se admite sensul acestei axe ca fiind in sensul de rotatie al paletei,
- axa principala de inertie al ariei sectiunii profilului, avand sensul catre bordul de fuga,
ξ - axa principala de inertie al ariei sectiunii profilului, avand sensul catre extradosul profilului,
R - axa paletei care trece prin centrul de greutate al sectiunii de baza a aerofoliei paletei.
Alte notatii utilizate:
φ - unghiul de torsiune al profilelor fata de sectiunea de baza a aerofoliei,
i - unghiul de incidenta al profilului,
ca - viteza axiala a aerului la intrarea in paleta,
u - viteza periferica a profilului paletei, u = R∙ω,
w - viteza relativa a aerului la intrarea in paleta,
viteza unghiulara,
![]() ,
,
n - turatia retelei, in ture pe minut,
P - forta de lovire a corpului strain la impactul cu paleta,
T - componenta fortei P, pe directia axei η,
N - componenta fortei P, pe directia axei ξ,
Ψ - coeficientul dinamic datorat impactului corpului strain cu paleta,
- coeficient de duritate al corpului strain, avand semnificatia unui coeficient de amortizare,
G - greutatea corpului strain, G = m∙g , in care
m - masa corpului,
g - aceleratia gravitatiei
In fig. 35, se prezinta schema de calcul si notatiile utilizate pentru paleta de compresor.
7. Paleta de rotor compresor torsionata, supusa numai la solicitarile din impactul cu corpul strain.
Fata de paleta, corpul strain se deplaseaza pe directia si cu marimea vitezei relative w, a aerului, si loveste paleta catre intradosul profilului, in sectiunea a-a, situata la distanta Lb, fata de sectiunea de baza b-b, a aerofoliei. (fig. 35). Corpul strain are o greutate G, iar viteza lui este w.
Asupra efectelor impactului influenteaza atat duritatea corpului strain, cat si ale materialului aerofoliei paletei, aprecierea acestei influente facandu-se prin coeficientul χ, care reprezinta raportul dintre duritatea corpului strain HB, si duritatea de referinta HB*.
Pentru paletele din otel aliat, duritatea Brinell este 2500 - 4200 [Mpa]. Paletele de compresor axial la primele trepte sunt executate din oteluri aliate si au bordurile de atac durificate, ca urmare, consideram o valoare medie HB* = 3000 [MPa], deci
![]()
In functie de natura corpului strain se va preciza si valoarea HB, respectiv a marimii coeficientului χ.
Valorile duritatilor pentru diferite materiale sunt urmatoarele:
|
Material |
HB |
HB |
|
|
[Mpa] |
Material |
[Mpa] |
|
|
Aluminiu |
Aliaje de aluminiu | ||
|
Aur |
Aliaje de magneziu | ||
|
Calciu |
Aliaje de cupru | ||
|
Bariu |
Bronzuri | ||
|
Cupru |
Bronz de aluminiu | ||
|
Crom |
Fonte | ||
|
Fier |
Fonte aliate | ||
|
Magneziu |
Otel carbon | ||
|
Molibden |
Otel usor aliat | ||
|
Nichel |
Otel usor aliat tratat | ||
|
Platina |
termic | ||
|
Titan |
Otel inalt aliat | ||
|
Vanadiu |
Materiale antifrictiune | ||
|
Volfram |
Babit | ||
|
Zinc |
Aliaje cu plumb | ||
|
Plumb |
Bronz pentru lagare | ||
|
Cositor |
Alama | ||
|
Siliciu |
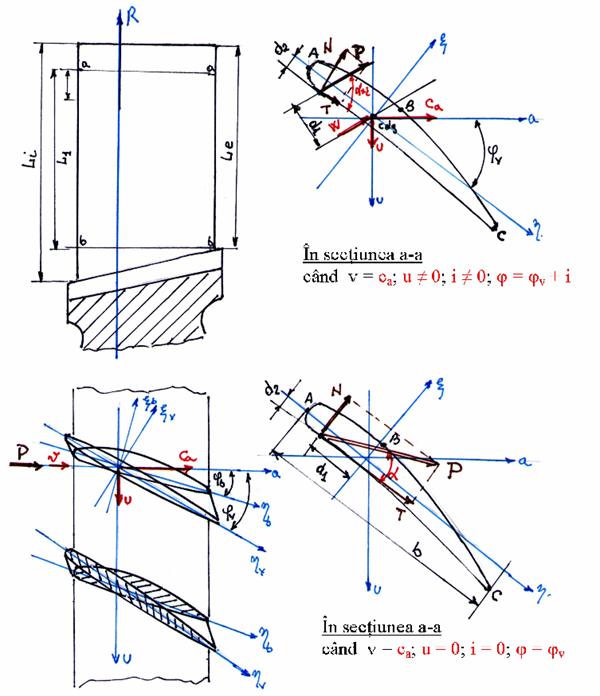
Fig. 35 - Schema de calcul a paletei de rotor compresor, treapta I.
Valori ale tensiunilor limita de curgere σd si limita de rezistenta pentru unele metale.
|
Material |
ar [Mpa] |
Go,2 [Mpa} |
ad [MPa] |
[Kg/m3] |
||
|
Aluminiu |
| |||||
|
Aur | ||||||
|
Bariu | ||||||
|
Calciu | ||||||
|
Cupru | ||||||
|
Crom | ||||||
|
Fier | ||||||
|
Magneziu | ||||||
|
Molibden | ||||||
|
Nichel | ||||||
|
Platina | ||||||
|
Titan | ||||||
|
Vanadiu | ||||||
|
Volfram | ||||||
|
Zinc | ||||||
|
Plumb | ||||||
|
Cositor | ||||||
|
Siliciu | ||||||
|
Aliaje de aluminiu | ||||||
|
Aliaje de magneziu | ||||||
|
Aliaje de cupru |
300-9oo | |||||
|
Aliaje de titan | ||||||
|
Bronz | ||||||
|
Bronz de aluminiu | ||||||
|
Fonte | ||||||
|
Fonte inalt aliate | ||||||
|
Otel carbon | ||||||
|
Otel usor aliat | ||||||
|
Otel aliat tratat | ||||||
|
Otel inalt aliat | ||||||
|
Material antifrictiune | ||||||
|
Babit | ||||||
|
Aliaje cu plumb | ||||||
|
Bronz pentru lagare | ||||||
|
Alama | ||||||
|
Beriliu | ||||||
|
Mangan |
Forta de contact P, se considera ca fiind concentrata in punctul de contact cu paleta si are marimea,
![]()
in care,
χ - coeficient de duritate,
Ψ - coeficient dinamic,
G - greutatea corpului strain.
Forta P, se descompune pe directiile axelor principale ξ, η, respectiv
![]()
![]()
Forta P produce:
a - tensiuni de forfecare τ, in planul sectiunii a-a al aerofoliei, aflat in zona de contact cu corpul strain,
![]()
A - aria sectiunii profilului in a-a.
b - tensiuni de torsiune Mr1, cand forta T este la distanta d2 fata de axa η,
![]()
si corespunzator tensiunile tangentiale
![]()
H - rigiditatea geometrica la torsiune a profilului din sectiunea a-a,
Cmax - grosimea maxima a profillului din sectiunea a-a
In sectiunea de baza aerofoliei b-b, foita T produce momentul incovoietor fata de axa ξb,
![]()
si tensiunile de incovoiere
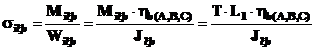
Wiξb - modulul de rezistenta la incovoiere in sectiunea b-b,
Jξb - momentul de inertie fata de axa ξ a sectiunii b-b,
η(A, B, C) - distantele η la punctele A, B, C, ale profilului din sectiunea b-b.
Forta N, produce in sectiunea a-a :
a - momentul de torsiune Mr2, si tensiunile tangentiale τ3,
![]()
si tensiunile
![]()
Ca urmare, in sectiunea a-a, se va dezvolta tensiunea tangentiala rezultanta
![]()
Sub actiunea momentului de rasucire Mr = Mr2 - Mrt, profilul paletei se va deforma catre extrados.
b - In sectiunea de baza b-b, a paletei, forta N va produce momentul incovoietor Miηb, fata de axa ηb,
![]()
c - Intr-o sectiune aflata la distanta x fata de punctul de impact,
![]() ,
,
iar tensiunile de incovoiere vor fi
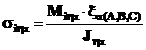
8 - Coeficientul dinamic
Relatia de calcul pentru coeficientul dinamic se stabileste considerand modul de fixare a paletei la capete.
Pentru paleta de rotor compresor, fara bandaj la capat, se considera ca aceasta este similara cu o bara incastrata la baza si libera la varf.
Coeficientul dinamic se obtine in acest caz din:
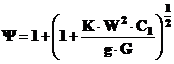
in care
K - rigiditatea paletei fata de axa dupa care se produce deformatia,
![]()
E - modul de elasticitate la incovoiere al materialului din care este executata paleta,
J - momentul de inertie fata de axa considerata a profilului.
Se noteaza:
G - greutatea corpului care loveste paleta,
G1 - greutatea aerofoliei paletei,
G2 - greutatea bandajelor dispuse pe aerofolie pentru rigidizare,
w - viteza relativa a aerului la intrarea in reteaua de palete.
Coeficientul dinamic Ψ va avea urmatoarele expresii:
1 - Paleta fara bandaje de rigidizare, considerand corpul strain lovind la varful paletei, greutatea aerofoliei fiind G1, sectiunea de calcul fiind la baza aerofoliei (sectiunea b-b), fig. 36,
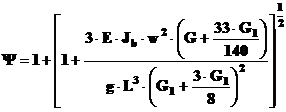

Fig. 36 - Schema de calcul.
2 - Pentru aceeasi paleta,
dar considerand o sectiune aflata la distanta x fata de punctul de impact, 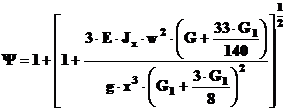
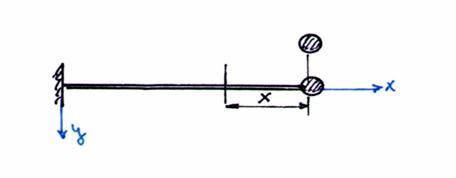
Fig. 37 - Schema de calcul.
3 - Paleta la care corpul strain loveste aerofolia intr-o sectiune aflata la distanta L1 fata de sectiunea de baza,
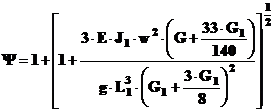
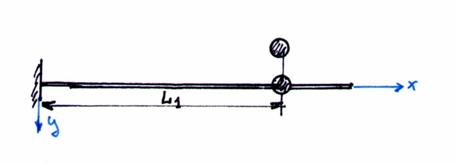
Fig. 38 - Schema de calcul.
4 - Paleta considerata ca o bara fara masa proprie, dar avand forma si dimensiunile geometrice reale. In acest caz, G1 = 0 si G2 = 0, paleta neavand elemente de rigidizare pe aerofolie.
Ca urmare, coeficientul C1 = 1, iar coeficientul dinamic este:
a - in sectiunea de baza b-b a paletei:
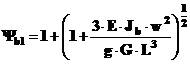
b - in sectiunea de la distanta x fata de punctul de impact:
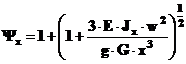
c - in sectiunea de baza b-b, cand punctul de impact pe paleta este dispus la distanta L1:
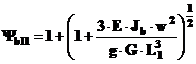
Viteza relativa a curentului de aer care intra in reteaua de palete w rezulta din considerarea vitezei axiale ca a aerului si a vitezei periferice a paletei u in sectiunea de impact:
![]()
ca - viteza axiala a aerului la intrarea in reteaua de palete,
u - viteza periferica a paletei in sectiunea considerata
![]()
ω - viteza unghiulara a retelei de palete,
![]()
n - turatia retelei, [rot / min]
R - raza de la centrul retelei pana la sectiunea de impact.
rezulta
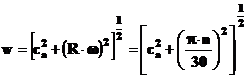
Pentru calculul parametrilor caracteristici profilului de paleta subsonic se pot folosi relatiile aproximative:
![]()
![]()
![]()
![]()
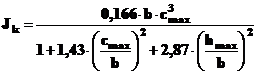
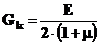
![]()
In aceste relatii s-a notat:
A - aria sectiunii profilului,
Jξ, Jη - momentele de inertie fata de axele principale ale profilului,
Jp - momentul de inertie polar al profilului,
Jk - momentul de inertie la torsiune al profilului,
Gk - modulul de elasticitate la torsiune al materialului paletei,
E - modulul de elasticitate la incovoiere al materialului paletei,
μ - coeficientul Poisson,
μ = 0,3 pentru domeniul deformatiilor elastice,
μ = 0,5 pentru domeniul deformatiilor plastice.
Wp = H - modulul de rezistenta la torsiune al profilului.
9. Calculul tensiunilor totale de incovoiere in punctele A, B, C, ale profilului, rezultate numai din impactul paletei cu un corp strain.
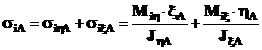
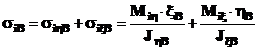
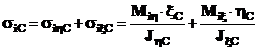
10. Deformatia unghiulara in lungul paletei.
Datorita torsionarii suplimentare a paletei, se produce o deformatie unghiulara θ in lungul aerofoliei, care rezulta din:
![]() , [radiani]
, [radiani]
in care:
![]()
τ - tensiunea tangentiala,
d - distanta de la punctul de impact la centrul de greutate al profilului,
L - lungimea aerofoliei de la punctul de impact la sectiunea de baza,
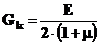
11. Rezultate experimentale.
Au fost efectuate determinari experimentale privitoare la efectele patrunderii unor corpuri straine in reteaua de palete ale unui rotor de ventilator de la un turboreactor cu dublu flux, in urmatoarele conditii:
- turatia rotorului: 3157 [rot / min],
- unghiul de dispunere a paletei pe coroana discului: 33°,
- locul de impact pe paleta: 20 % din marimea corzii profilului aflat catre varful paletei,
- masa pasarii: 1 kg.
- viteza pasarii la impact, 283 [m / sec]
- durata de impact a pasarii cu paleta: 0,5 [msec]
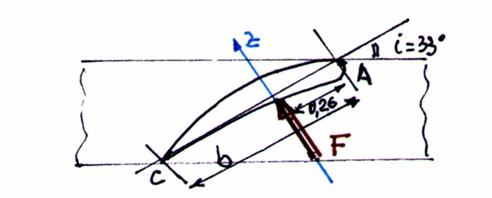
Fig. 39 - Schema profilului si punctul de impact.
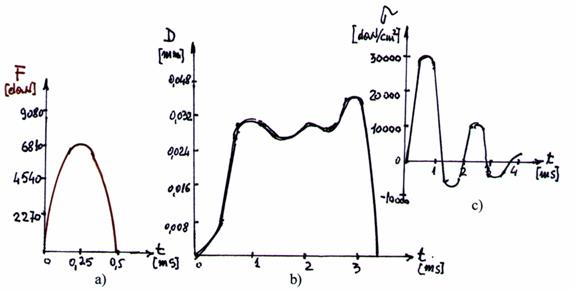
Fig. 40 - Rezultatele experimentarii.
a) variatia fortei de impact in timp; b) variatia deplasarii paletei in timp;
c) variatia tensiunilor de impact in timp.
Tensiunile cele mai mari se produc la sfarsitul impactului 0,5 [msec], dupa care valoarea lor se amortizeaza in timp de 4-5 [sec].
Deplasarea paletei creste brusc, apoi ramane
aproximativ
Cresterea brusca a tensiunii duce la aparitia unor deformatii sau distrugeri locale, si chiar la ruperea paletei.
Ruperea paletei se poate face si din sectiunea de la baza aerofoliei
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |