
Cậmpul electric si potentialul unei sfere incarcate uniform cu sarcina electrica
Cậmpul electric al unei sfere incarcate uniform cu sarcina electrica.
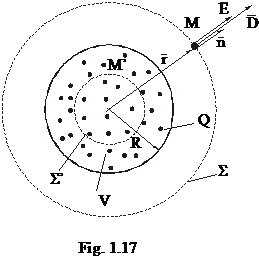 Fie o sfera de volum V incarcata uniform cu sarcina
electrica, densitatea de volum a sarcinii electrice fiind v
Fie o sfera de volum V incarcata uniform cu sarcina
electrica, densitatea de volum a sarcinii electrice fiind v
Consideram suprafata inchisa Σ concentrica cu sfera ; din motive de simetrie campul este radial. Pentru un punct M situat in exteriorul sferei avem:
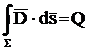
![]()
![]()
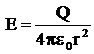
Daca punctul este in interiorul sferei si suprafata de integrare Σ' trece prin M' rezulta:
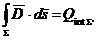
![]()
![]()
![]() ,
, ![]()
Potentialul sferei uniform incarcate cu sarcina electrica
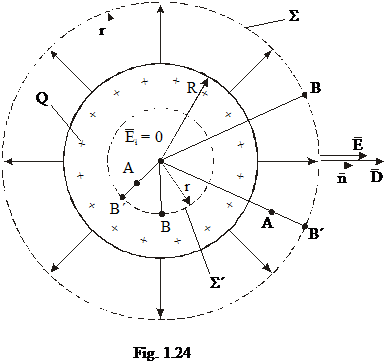
Presupunem o sfera
incarcata uniform cu sarcina electrica de densitate v (fig. 1.24):
Pentru punctele situate in exteriorul sferei demonstratia este similara cu aceea din cazul sarcinii punctiforme. Potentialul in punctul exterior sferei este:
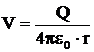
In interior unde r < R vom avea:
![]()
![]()
![]()
![]() sau
sau 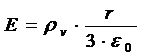
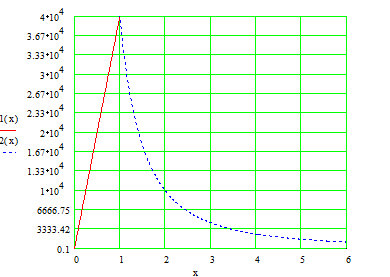
Intensitatea campului electric in centrul sferei este zero.
Potentialul unui punct din sfera este:
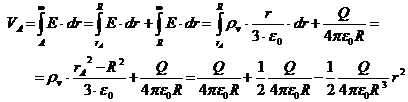
Se observa ca in punctele de pe sfera, r = R, se verifica relatia:
![]()
In centrul sferei, r = 0, potentialul este maxim:
![]()
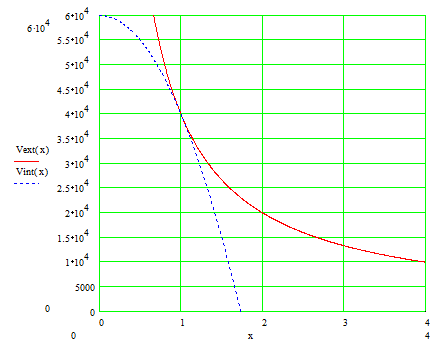
In figura de se reprezinta variatia potentialului in functie de raza r atat pentru punctele situate in exteriorul sferei cat si in interiorul sferei.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |