
1. Generalitati
Problema sintezei sistemelor automate liniare consta in determinarea schemei bloc si a schemei de principiu pe baza performantelor impuse sau a unor parametri functionali in special a sistemelor continue. Problema sintezei se leaga de alegerea unui anumit tip de schema si pentru generalizare vom considera cea mai complicata schema a unui sistem continuu : cazul sistemului de reglare automata. Oricat de complicat ar fi un sistem de reglare automat el poate fi structurat prin transformari echivalente si prezentat printr-o schema bloc ca in fig.1 in care blocul G1(s) contine toate elementele dispozitivului de automatizare DA, avand ca baza regulatorul, iar blocul G2(s) reprezinta oobiectul automatizarii sau procesul supus reglarii. Asupra acestora actioneaza perturbatiile Z(s).
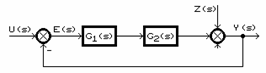
Fig.1.
Pentru realizarea sintezei trebuie sa cunoastem :
blocul G2(s) (procesul) sau modelul sau matematic;
tipul perturbatiilor z;
calitatile sistemului automat in ansamblu;
marimea de iesire y.
Problema sintezei reprezinta din punct de vedere matematic determinarea structurii sistemului, deci a blocului G1(s) pe baza cunoasterii obiectului automatizat G2(s), tipul perturbatiilor, calitatile sistemului si a marimii de iesire y.
Blocul G2(s) se determina in cazul existentei sistemului prin incercari asupra acestuia. Identificarea reprezinta determinarea structurii obiectului automatizarii sau functiei de transfer G2(s) pe baza cunoasterii principiului de functionare si performantelor sale. In concluzie prima etapa a sintezei consta in identificare.
Consideram ca aplicam la intrare un semnal treapta unitara si obtinem raspunsul care are forma din figura 2.a. Din grafic, ducand tangenta in punctul de inflexiune se determina constantele kp, T0 si T. Cu aceste aproximari se poate scrie functia de transfer a procesului sub forma :
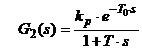
care reprezinta o aproximare a raspunsului y(t) ca in figura 2.b.
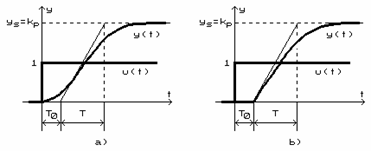
Figura 2.
Daca T0≤5%T atunci timpul mort T0 se neglijeaza si procesul este aproximat cu un element aperiodic de ordinul intai :
![]()
Daca iesirea y(t) prezinta mai multe puncte de inflexiune, obtinem prin identificare urmatoarele situatii pentru G2(s), forme cu doua sau mai multe constante de timp de intarziere :
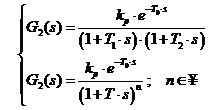
Dupa identificarea procesului si obtinerea lui G2(s) se poate face sinteza prin urmatoarele patru metode:
1) corectia sistemelor automate;
2) alegerea si acordarea regulatoarelor automate;
3) sinteza prin metoda directa;
4) sinteza prin metoda ecuatiilor de stare.
Corectia sistemelor automate consta in alegerea pe baza experientei practice a unui regulator universal sau specializat cu o anumita functie de transfer. Se implementeaza regulatorul in cadrul SRA si se fac incercari, masurandu-se parametrii, obtinand performantele sistemului. Daca aceste performante nu satisfac conditiile impuse prin tema de automatizare, prin conectarea in serie, paralel sau antiparalel cu regulatorul a unor retele de corectie se poate imbunatati regimul dinamic al SRA.
Daca dispozitivul de automatizare sau regulatorul automat se alege sub forma prefabricata industrial, atunci prin sinteza se urmareste sa se aleaga tipul de regulator impus de performantele sistemului si in acordarea constantelor sale interne corespunzatoare constentelor procesului.
Sinteza prin metoda directa este cea mai eficace metoda. Dupa identificarea procesului (determinarea functiei de transfer G2(s)), prin diferite moduri (utilizarea diagramelor de frecventa, repartitia poli-zerouri, metoda analitica directa) se obtine functia functia de transfer G1(s) a dispozitivului de automatizare.
Sinteza prin metoda ecuatiilor canonice de stare este o metoda moderna de sinteza aplicabila si in cazul sistemelor multivariabile. In acest caz se urmareste determinarea matricei de transfer a regulatorului pe baza ecuatiilor canonice ale sistemelor automate liniare.
Daca sinteza se face tinand seama de o singura marime de intrare (intrarea propriu-zisa U(s) sau perturbatia Z(s)) spunem ca sinteza este cu un singur grad de libertate.
Daca se iau in considerare in procesul de sinteza influientele atat a intrarii propriu-zise U(s) cat si a perturbatiei Z(s)) spunem ca sinteza este cu doua grade de libertate.
Consideram sistemul de reglare automata din figura 1. Functia de transfer corespunzatoare sistemuli deschis este :
![]()
Pentru rezolvarea problemei sintezei cu doua grade de libertate se considera ca asupra sistemului actioneaza fie numai intrarea propriu-zisa U(s) fie numai perturbatia Z(s). Corespunzator avem urmatoarele functii de transfer :
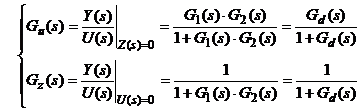
In cazul considerarii celor doua grade de libertate vom avea matricea de transfer G(s) de forma :
![]()
ceea ce ne arata ca sinteza sistemelor cu doua grade de libertate nu se deosebeste esential de sinteza cu un singur grad de libertate deoarece, daca s-a determinat functia de transfer Gd(s) a sistemului deschis, matricea de transfer G(s) este unic determinata.
Este metoda de sinteza a sistemelor automate liniare la care se corecteza comportarea in regim dinamic, folosid retele derivate sau automatizatoare. Necesitatea cerintei apare pentru imbunatatirea performantelor atat in regim stationar cat si in regim dinamic. In regimul stationar, eroarea statica trebuie sa fie mai mica decat o valoare maxima < max. In regim dinamic suprareglarea trebuie sa fie inferioare valorilor maxime < max pentru amortizarea rapida a oscilatiilor, factorul de amortizare trebuie sa fie mai mare > min, durata procesului tranzitoriu trebuie sa fie mica tpt<tpt max.
Alegerea dispozitivului de automatizare sau a unui regulator industrial produs de o uzina specializata se face in functie performantele statice si dinamice cerute de catre proces. De asemenea se tine seama de tipul procesului care se regleaza si de constantele kp, T0 , T din functia de transfer a procesului (rezultata din identificare) ca in tabelul 1.
Tabelul 1
|
Parametrul reglat |
T0/T |
k |
T |
z(t) |
Regulator |
|
mare |
neliniar de tip releu |
||||
|
Nivel |
<1 |
mare |
mica |
P |
|
|
<1 |
mare |
mare |
PI |
||
|
Debite si concentratii |
<1 |
mare |
mic |
PI |
|
|
Presiuni |
<1 |
mare |
mare |
PI |
|
|
mic |
PID |
||||
|
Temperatura |
<1 |
mare |
PI |
||
|
mic |
PID |
||||
|
>1 |
mic |
PD |
|||
|
mare |
PD,PID |
Dupa ce SRA a fost conceput, se face analiza regimului dinamic al acestuia si se verifica daca performantele corespund exigentelor cerute. In cazul in care cerintele nu sunt indeplinite se face corectia SRA prin retele de corectie simple de tip derivativ (cu avans de faza), integrator (cu intarziere de faza) si integro-derivativ (cu intarziere si avans de faza).
3. Retea de corectie derivativa (cu avans de faza)
O retea de corectie RC derivativa este prezentata in figura 3.a. Considerand ca circuitul functioneaza in gol , dupa efectuarea calculelor se obtine functia de transfer :
![]()
unde T - constanta de timp :
![]()
a - factorul de avans :
![]()
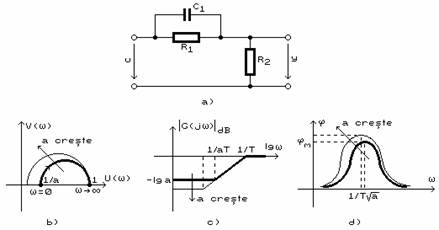
Figura 3.
Caracteristicile de frecventa sunt prezentate in figurile 3.b ÷ 3.d si sunt utilizate la dimensionarea marimilor R1, R2, C1 in functie de datele de corectie necesare.
Introducand o astfel de retea de corectie se imbunatateste stabilitatea, creste rapiditatea raspunsului si amortizarea.
4. Retea de corectie integratoare (cu intarziere de faza)
O retea de corectie RC integratoare este prezentata in figura 5.a. Considerand ca circuitul functioneaza in gol , dupa efectuarea calculelor se obtine functia de transfer :
![]()
unde T - constanta de timp :
![]()
a - factorul de avans :
![]()
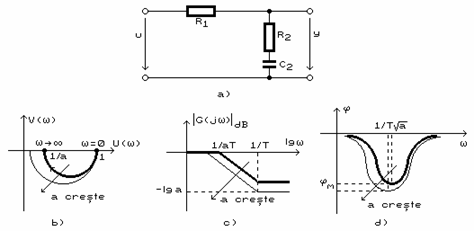
Figura 4.
Caracteristicile de frecventa sunt prezentate in figurile 4.b ÷ 4.d si sunt utilizate la dimensionarea marimilor R1, R2, C2 in functie de datele de corectie necesare.
Introducand o astfel de retea de corectie se imbunatateste precizia, se reduce eroarea stationara, dar se inrautateste stabilitatea.
5. Retea de corectie integro-derivativa (cu intarziere si avans de faza)
O retea de corectie RC integro-derivativa este prezentata in figura 5.a. Considerand ca circuitul functioneaza in gol , dupa efectuarea calculelor se obtine functia de transfer :
![]()
unde : Ti -
![]()
Td - constanta de timp de derivare :
![]()
a - factorul de avans :
![]()
Caracteristicile de frecventa sunt prezentate in figurile 5.b ÷ 5.d si sunt utilizate la dimensionarea marimilor R1, R2, C2 in functie de datele de corectie necesare.
O astfel de retea de corectie imbina calitatile retelei derivative si retelei integratoare.
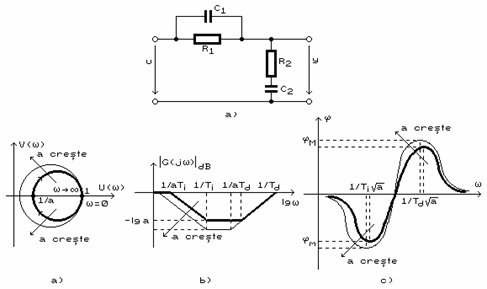
Figura 5.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |