
ELEMENTE DE TEORIE GENERALA A CONVERSIEI
ELECTROMECANICE A ENERGIEI
1. CLASIFICAREA MASINILOR SI TRANSFORMATOARELOR ELECTRICE
Masina electrica este un convertor electromecanic de energie care poate realiza convertirea energia mecanica in energie electromagnetica sau invers. Din acest punct de vedere deci masina electrica este reversibila
Privite ca un convertor de energie, masinile electrice se pot imparti in trei clase:
a)-masini electrice inductive la care campul activ este un camp magnetic;
b)-convertoare capacitive la care convertirea energiei mecanice in electromagnetica si invers se face cu ajutorul campului electric;
c)-convertoare inductiv-capacitive la care convertirea energiei se face cu ajutorul campului magnetic si electric
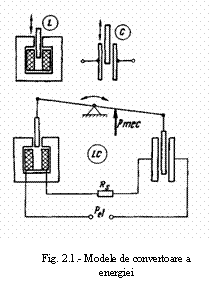 Schemele de principiu pentru aceste tipuri de masini sunt
date in figura 1. La convertoare de tip inductiv conversia energiei se
realizeaza ca urmare a modificarii inductivitatii, iar la
convertoare de tip capacitiv ca urmare a modificarii capacitatii
electrice a sistemului. La convertoare de tip inductiv- capacitiv in cazul cel
mai simplu se unifica intr-un singur sistem electromecanic cele doua tipuri de convertoare: inductiv si capacitiv.
Convertoare de tip capacitiv in general nu se intalnesc in practica
industriala (desi au fost primele convertoare aparute) dar se
incearca o implementare oarecare a convertoarelor de tip inductiv-
capacitiv utilizand fenomenele de magnetostrictiune si de piezoelectricitate.
Schemele de principiu pentru aceste tipuri de masini sunt
date in figura 1. La convertoare de tip inductiv conversia energiei se
realizeaza ca urmare a modificarii inductivitatii, iar la
convertoare de tip capacitiv ca urmare a modificarii capacitatii
electrice a sistemului. La convertoare de tip inductiv- capacitiv in cazul cel
mai simplu se unifica intr-un singur sistem electromecanic cele doua tipuri de convertoare: inductiv si capacitiv.
Convertoare de tip capacitiv in general nu se intalnesc in practica
industriala (desi au fost primele convertoare aparute) dar se
incearca o implementare oarecare a convertoarelor de tip inductiv-
capacitiv utilizand fenomenele de magnetostrictiune si de piezoelectricitate.
Pe de
alta parte, toate convertoarele de tip inductiv se pot impartii
in doua grupe mari: masini de c.a. si masini de c.c.
Convertoarele de c.a. se impart in masini asincrone, masini
sincrone, masini cu colector de c.a. si transformatoare. La
masinile sincrone viteza unghiulara a rotorului ![]() (indicele 2 se va referi totdeauna la rotorul unei
masini sau la secundarul unui transformator) si viteza
unghiulara a campului magnetic
(indicele 2 se va referi totdeauna la rotorul unei
masini sau la secundarul unui transformator) si viteza
unghiulara a campului magnetic ![]() (indicele l se va referi totdeauna la statorul unei
masini sau la primarul unui transformator) sunt egale intre ele, pe cand
la masinile asincrone totdeauna
(indicele l se va referi totdeauna la statorul unei
masini sau la primarul unui transformator) sunt egale intre ele, pe cand
la masinile asincrone totdeauna ![]() , iar sensurile de rotire a rotorului si ale campului
magnetic statoric pot fi chiar contrare.
, iar sensurile de rotire a rotorului si ale campului
magnetic statoric pot fi chiar contrare.
Masinile de c.a. cu colector se deosebesc de masinile sincrone si asincrone prin aceea ca poseda un sistem mecanic de convertire a frecventei si a numarului de faze denumit colector, care se racordeaza fie cu infasurarea rotorica, fie cu cea statorica a masinii.
Transformatoarele electrice sunt convertoare electromagnetice de energie: in cadrul lor nu se realizeaza transformarea energiei mecanice in electromagnetica si invers, ci se realizeaza convertirea energiei electromagnetice tot in energie electromagnetica dar cu alti parametri decat cei initiali. Transformatoarele se realizeaza astfel incat infasurarile lor nu se deplaseaza unele in raport cu altele, deci in cadrul lor vom avea indusa numai t.e.m. de transformare.
Dupa regimul de lucru masinile electrice se pot imparti, de asemenea, in doua:
a) regimul de generator al masinii in cadrul caruia energia mecanica aplicata arborelui masinii este transformata in energie electromagnetica, care este cedata unei retele oarecare de alimentare; sensul puterii electrice este deci dinspre masina catre retea;
b) regimul de motor al masinii in cadrul caruia energia electromagnetica aplicata la bornele masinii este convertita in energie mecanica, care este cedata prin arborele sau unui dispozitiv (masina) de lucru; sensul puterii electrice in acest caz este dinspre reteaua de alimentare catre masina de lucru.
Ca o regula mai generala masinile electrice se executa dintr-o parte ce realizeaza o miscare de rotatie denumita rotor si o parte fixa denumita stator. Cand se roteste numai rotorul se spune ca masina are un singur grad de libertate; astfel de masini se numesc unidimensionale. Dar in general cuplul electromagnetic al unei masini se aplica atat rotorului cat si statorului ,iar daca i se va permite si statorului sa se roteasca, atunci intr-adevar acesta se va roti si el in sens invers sensului de rotire al rotorului. Despre o masina la care se poate roti atat statorul cat si rotorul, se spune ca are doua grade de libertate si o astfel de masina se numeste bidimensionala.
In sfarsit, la unele dispozitive de navigatie rotorul masinii poate fi si sub forma unei sfere care se roteste dupa doua axe dispuse la 900, iar o astfel de masina are trei grade de libertate si se numeste tridimensionala. In electromecanica cosmica se utilizeaza uneori sisteme electromecanice sasedimensionale la care atat rotorul cat si statorul au fiecare cate trei grade de libertate.
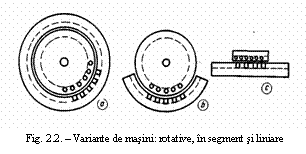 La unele masini electrice in loc de miscare de
rotatie se produce o miscare de translatie cu revenire.
La astfel de masini statorul si rotorul sunt 'deschise',
ceea ce duce la reflectarea campului magnetic la capetele statorului
(rotorului), iar aceasta la randul sau duce la deformarea campului
magnetic din intrefier, respectiv la inrautatirea parametrilor
energetici ai masinii. In figura 2, se arata cum se ajunge de la o
masina electrica cu rotorul si statorul de tip cilindric,
la o masina cu statorul 'in segment', respectiv la una cu
statorul si rotorul liniar. Masina electrica liniara
se utilizeaza in practica numai in regimul de motor.
La unele masini electrice in loc de miscare de
rotatie se produce o miscare de translatie cu revenire.
La astfel de masini statorul si rotorul sunt 'deschise',
ceea ce duce la reflectarea campului magnetic la capetele statorului
(rotorului), iar aceasta la randul sau duce la deformarea campului
magnetic din intrefier, respectiv la inrautatirea parametrilor
energetici ai masinii. In figura 2, se arata cum se ajunge de la o
masina electrica cu rotorul si statorul de tip cilindric,
la o masina cu statorul 'in segment', respectiv la una cu
statorul si rotorul liniar. Masina electrica liniara
se utilizeaza in practica numai in regimul de motor.
Un loc deosebit il au masinile indicatoare din sistemele de automatizare, care de fapt sunt traductoare ce transforma o informatie numerica intr-o deplasare unghiulara sau liniara. Exista, de asemenea, o multitudine de masini electrice care lucreaza sub pamant, in imersie, in cosmos.
Aproape tonte convertoarele de tip inductiv executa miscarea de rotatie, statorul lor fiind fix, dar isi gasesc aplicatii si masinile cu miscarea de translatie repetitiva, respectiv cu o miscare oscilanta sau sacadata ('pas cu pas' - de impuls) a rotorului, dupa cum se utilizeaza si unele masini electrice cu un rotor de tip lichid sau gazos.
TIPURILE CONSTRUCTIVE DE BAZA ALE MASINILOR ELECTRICE
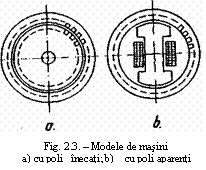 Independent de tipul curentului electric al masinii - c.c.
sau c.a.- din punct de vedere constructiv masinile electrica se impart in
doua grupe: cu poli inecati, respectiv cu poli
aparenti - figura 3 a si b. La masinile cu poli inecati
avem un intrefier uniform si reluctantele magnetice au aceeasi
valoare dupa toate directiile, iar infasurarile
excitatiei se distribuie uniform pe diverse crestaturi rotorice sau
statorice. La masini cu poli aparenti infasurarea de
excitatie este concentrata ( in figura 3 b ea este montata pe
polii rotorici), se pot evidentia in mod clar: axa longitudinala
(in lungul polilor) si axa transversala ( bisectoarea unghiului
dintre doi poli vecini), in lungul carora intrefierul masinii ca
si reluctantele magnetice difera esential. De fapt polii
aparenti (cu infasurarea de excitatie concentrata
corespunzatoare) pot fi prevazuti fie in rotor, fie in stator.
Independent de tipul curentului electric al masinii - c.c.
sau c.a.- din punct de vedere constructiv masinile electrica se impart in
doua grupe: cu poli inecati, respectiv cu poli
aparenti - figura 3 a si b. La masinile cu poli inecati
avem un intrefier uniform si reluctantele magnetice au aceeasi
valoare dupa toate directiile, iar infasurarile
excitatiei se distribuie uniform pe diverse crestaturi rotorice sau
statorice. La masini cu poli aparenti infasurarea de
excitatie este concentrata ( in figura 3 b ea este montata pe
polii rotorici), se pot evidentia in mod clar: axa longitudinala
(in lungul polilor) si axa transversala ( bisectoarea unghiului
dintre doi poli vecini), in lungul carora intrefierul masinii ca
si reluctantele magnetice difera esential. De fapt polii
aparenti (cu infasurarea de excitatie concentrata
corespunzatoare) pot fi prevazuti fie in rotor, fie in stator.
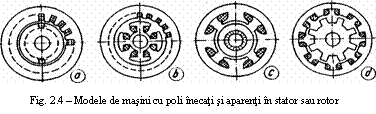
Variantele constructive cu poli inecati si poli aparenti sunt cele mai raspandite: masinile asincrone sunt executate cel mai adesea .in varianta cu poli inecati, iar masinile sincrone in varianta cu poli aparenti (fig. 4 a si b). Varianta cu poli aparenti in stator (fig.4 c) este specifica masinilor de c.c., iar varianta cu poli aparenti in rotor si in stator (fig.4 d) se intalneste mai ales la masinile parametrice la care conversia energiei se realizeaza pe baza modificarii periodice a reluctantei magnetice a intrefierului.
 La o masina asincrona (cu poli inecati)
circuitul magnetic al statorului se executa din tole de tabla
electrotehnica de 0,5 mm, izolate intre ele si apare sub forma unui
cilindru gol in interior (golul corespunzator cilindrului rotoric, intre
ele fiind intrefierul). In interiorul sau in lungul generatoarelor
cilindrului sunt executate crestaturile (numite si ancose)
statorice in care se monteaza infasurarea respectiva.
Rotorul are circuitul magnetic realizat, de asemenea, din tole de tabla
electrotehnica, iar la exteriorul sau sunt executate
crestaturile rotorice in care se monteaza infasurarea in
scurtcircuit sau bobinata.
La o masina asincrona (cu poli inecati)
circuitul magnetic al statorului se executa din tole de tabla
electrotehnica de 0,5 mm, izolate intre ele si apare sub forma unui
cilindru gol in interior (golul corespunzator cilindrului rotoric, intre
ele fiind intrefierul). In interiorul sau in lungul generatoarelor
cilindrului sunt executate crestaturile (numite si ancose)
statorice in care se monteaza infasurarea respectiva.
Rotorul are circuitul magnetic realizat, de asemenea, din tole de tabla
electrotehnica, iar la exteriorul sau sunt executate
crestaturile rotorice in care se monteaza infasurarea in
scurtcircuit sau bobinata.
In general insa circuitele magnetice pe care se monteaza infasurari strabatute de c.a. se executa din tole de tabla electrotehnica izolate intre ele, iar daca infasurarile sunt strabatute de c.c. circuitele magnetice pot fi masive cu profile constructive adecvate. Astfel, de exemplu, la masini sincrone in rotor avem in general infasurari alimentate in c.c., de aceea rotorul este masiv iar infasurarile respective se monteaza (la turbageneratoare) in crestaturi, realizate in corpul masiv al rotorului prin frezare.
De obicei rotorul (partea mobila) se gaseste in interiorul statorului, uneori insa rotorul este montat la exteriorul statorului cilindric - astfel de masini se numesc cu rotor exterior. Masinile cu rotor exterior au un moment axial de inertie mare si ele se utilizeaza in general in actionari la care este necesar un astfel de moment de inertie.
In unele cazuri se folosesc masini de c.c. cu poli de excitatie rotitori si masini sincrone cu poli de excitatie fixati in stator - astfel de masini se numesc inversate.
 Masinile electrice se mai deosebesc intre ele prin forma
protectiei impotriva patrunderii corpurilor solide si a picaturilor de apa in
masina. Codificarea acestor protectii in tara noastra
se face prin literele IP urmate de doua cifre: prima cifra (0.6)
exprima gradul protectiei mecanice impotriva patrunderii
corpurilor solide in interiorul masinii si atingerii
partilor aflate sub tensiune; a doua cifra (0..8) exprima
gradul de protectie al masinii contra apei. Semnificatiile pentru
prima cifra sunt: 0 - fara protectie; l - protejat contra
corpurilor solide cu grosimi mai mari de 50 mm; 2 - idem 12 mm; 3 - idem 2,5
mm; 4 - idem 1,0 mm; 5 - protejat partial contra prafului; 6 - protejat
total contra prafului. Semnificatiile pentru cea de a doua cifra
sunt: 0 - fara protectie; l - protejat contra picaturilor
de apa de condensatie; 2 - protejat contra picaturilor de
apa ce cad sub un ungi de maximum 15° fata de verticala locului;
3 - protejat contra apei sub forma de ploaie; 4 - protejat contra stropirii cu
apa; 5 - protejat contra jeturilor de apa sub presiune; 6- protejat
contra conditiilor de pe puntea navelor; 7 - protejat contra imersiei in
apa; 8 - folosirea ca utilaj submersibil.
Masinile electrice se mai deosebesc intre ele prin forma
protectiei impotriva patrunderii corpurilor solide si a picaturilor de apa in
masina. Codificarea acestor protectii in tara noastra
se face prin literele IP urmate de doua cifre: prima cifra (0.6)
exprima gradul protectiei mecanice impotriva patrunderii
corpurilor solide in interiorul masinii si atingerii
partilor aflate sub tensiune; a doua cifra (0..8) exprima
gradul de protectie al masinii contra apei. Semnificatiile pentru
prima cifra sunt: 0 - fara protectie; l - protejat contra
corpurilor solide cu grosimi mai mari de 50 mm; 2 - idem 12 mm; 3 - idem 2,5
mm; 4 - idem 1,0 mm; 5 - protejat partial contra prafului; 6 - protejat
total contra prafului. Semnificatiile pentru cea de a doua cifra
sunt: 0 - fara protectie; l - protejat contra picaturilor
de apa de condensatie; 2 - protejat contra picaturilor de
apa ce cad sub un ungi de maximum 15° fata de verticala locului;
3 - protejat contra apei sub forma de ploaie; 4 - protejat contra stropirii cu
apa; 5 - protejat contra jeturilor de apa sub presiune; 6- protejat
contra conditiilor de pe puntea navelor; 7 - protejat contra imersiei in
apa; 8 - folosirea ca utilaj submersibil.
Sub aspect constructiv masinile electrice se deosebesc si din punct de vedere al sistemului de racire. La masini cu racirea naturala circulatia aerului se realizeaza ca urmare a efectului de ventilare datorat rotirii partilor mobile ale masinii si a convectie.
La masini cu autoventilatie pe arborele masinii sunt montate paletele unui ventilator, iar la masini inchise racirea se face prin ventilatia fortata la exteriorul acesteia. Masinile cu ventilatia interna se impart in categorii de masini cu ventilatia axiala, radiala sau axial-radiala.
Pentru racirea masinilor ca agent de racire se poate utiliza aerul, hidrogenul, uleiul sau apa.
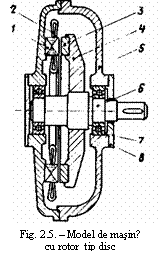
In practica se mai intalnesc masinile la care statorul si rotorul sunt sub forma de disc -fig. 5 Energia campului magnetic in acest caz se concentreaza in intrefierul format dintre discul statoric si cel rotoric. In figura 5 sunt mentionate: l - circuitul magnetic al statorului; 2 - infasurarea statorului; 3 - magneti permanenti; 4- circuitul magnetic al rotorului; 5 - scutul lateral; 6 - arborele; 7 - rulmentii; 8 - capacele casei rulmentilor.
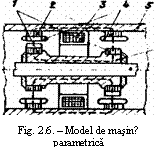
Masinile parametrice cele mai raspandite sunt cele cu doua rotoare (1) si statoare (2)-figura 6.
La o rotire a rotorului cu 90 reluctanta magnetica nu se schimba si in infasurarea (3) de excitatie nu se induce componenta variabila de tensiune. In acest caz de la infasurarile de curent alternativ (4), dispuse pe polii fiecarui stator, se culege o tensiune alternativa. Fluxul de excitatie al masinii se inchide prin miezul statoric (5) si miezul rotoric (6), montat pe arborele masinii (7).
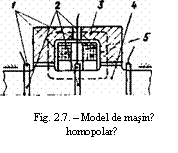
 In vederea obtinerii unor curenti continui mari (~100
kA) la tensiuni mici (cazul instalatiilor de galvanoplastie) se folosesc masini
unipolare sau homopolare. La astfel de masini nu exista colector,
dar in practica se utilizeaza perii colectoare (1) si inele
colectoare (2). Fluxul magnetic constant se inchide prin armatura
statorica (3) prin masivul rotoric (4) si doua spatii de
intrefier -- figura 7. Fluxul de excitatie (traseul sau este
mentionat prin linia punctata) este produs de infasurare
de excitatie(5) Curentul continuu este indus in masivul rotorului si
este cules cu ajutorul periilor (1). Pentru a micsora pierderile datorate
curentilor foarte mari, in masivul rotorului se executa unele
crestaturi in care se monteaza bare din cupru care se sudeaza de
inelele colectoare (2) formand un fel de infasurare rotorica in
scurtcircuit.
In vederea obtinerii unor curenti continui mari (~100
kA) la tensiuni mici (cazul instalatiilor de galvanoplastie) se folosesc masini
unipolare sau homopolare. La astfel de masini nu exista colector,
dar in practica se utilizeaza perii colectoare (1) si inele
colectoare (2). Fluxul magnetic constant se inchide prin armatura
statorica (3) prin masivul rotoric (4) si doua spatii de
intrefier -- figura 7. Fluxul de excitatie (traseul sau este
mentionat prin linia punctata) este produs de infasurare
de excitatie(5) Curentul continuu este indus in masivul rotorului si
este cules cu ajutorul periilor (1). Pentru a micsora pierderile datorate
curentilor foarte mari, in masivul rotorului se executa unele
crestaturi in care se monteaza bare din cupru care se sudeaza de
inelele colectoare (2) formand un fel de infasurare rotorica in
scurtcircuit.
 La convertoarele electromagnetice - transformatoarele electrice -
infasurarile se monteaza astfel incat este exclusa
deplasarea lor una fata de alta. Circuitul magnetic este format din
tole de tabla electrotehnica de 0,35 mm izolate intre ele.
La convertoarele electromagnetice - transformatoarele electrice -
infasurarile se monteaza astfel incat este exclusa
deplasarea lor una fata de alta. Circuitul magnetic este format din
tole de tabla electrotehnica de 0,35 mm izolate intre ele.
Pentru limitarea curentilor de scurtcircuit in anumite portiuni ale instalatiilor electrice industriale se utilizeaza asa-numitele reactoare, care reprezinta de fapt niste bobine cu miez sau fara miez de fier. In ultima perioada se utilizeaza si acumulatoarele inductive supraconductoare de energie magnetica (se ajunge la 100MJ de energie acumulata) cu inductii pana la 5T.
Oricat de diversificate ar fi insa masinile electrice, ele reprezinta insa doar niste convertoare electromecanice sau electromagnetice de energie, se supun acelorasi legi si evident au una si aceeasi prezentare matematica.
3. LEGILE DE BAZA ALE CONVERSIEI ELECTROMECANICE A ENERGIEI
Electromecanica poate fi privita ca o aplicatie a Electrotehnicii in domeniul tehnic in care se realizeaza conversia energiei. In acest fel electromecanicii ii pot fi atribuite cateva legi specifice.
PRIMA LEGE: conversia electromecanica a energiei nu se poate realiza cu randamentul de l00%..
In general nu se va gresi prea mult daca se face afirmatia ca intregul nostru mediu inconjurator este format din convertoare de energie, iar toate convertoarele de energie pot fi impartite in doua grupe: convertoare simple si convertoare complexe.
In cadrul convertoarelor simple intreaga energie de un tip se transforma integral in energie de alt tip. Un exemplu obisnuit este acela al cuptorului electric in care energia electrica se transforma integral in energie termica.
In cadrul convertoarelor complexe (si ele sunt cele mai numeroase) energia de un tip se converteste in alte doua (mai rar trei) tipuri de energie. Exemple de astfel de convertoare sunt cele ce realizeaza de exemplu convertirea energiei luminoase in cea electrica, a energiei chimice in cea mecanica etc. Dar in cadrul convertoarelor complexe colateral apare si o convertire partiala a energiei initiale in cea termica. Trebuie sa precizam un anumit aspect in legatura cu un cuptor electric: se vorbeste in tehnica de un randament al cuptorului, dar el este legat de faptul ca nu toata energia termica produsa in cuptor este utilizata in cadrul unui anumit proces tehnologic si sub acest aspect desigur ca randamentul cuptorului este subunitar. Acest randament insa nu este legat de conversia energiei electrice in cea termica, care se realizeaza integral,
 Convertoarele electromecanice si electromagnetice fac parte din
convertoarele complexe, avand in vedere ca in cadrul lor conversia
energiei electromagnetice sau a celei mecanice este insotita
intotdeauna si de componenta termica.
Convertoarele electromecanice si electromagnetice fac parte din
convertoarele complexe, avand in vedere ca in cadrul lor conversia
energiei electromagnetice sau a celei mecanice este insotita
intotdeauna si de componenta termica.
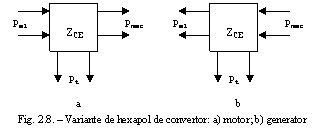
Sub forma sa cea mai generala convertorul
electromecanic de energie poate fi prezentat ca un hexapol cu o
impedanta interna ![]() ca in figura 8, Aici sunt figurate doua porti
electrice, doua porti pentru parametri mecanici si doua
porti pentru parametri termici (fig 8.a - regimul de motor al
convertorului, fig. 8.b - regimul de generator).
ca in figura 8, Aici sunt figurate doua porti
electrice, doua porti pentru parametri mecanici si doua
porti pentru parametri termici (fig 8.a - regimul de motor al
convertorului, fig. 8.b - regimul de generator).
La constructia convertorului electromecanic se cauta micsorarea fluxului termic ceea ce conduce la micsorarea gabaritelor, respectiv a costurilor convertorului. La ora actuala se executa masini electrice cu h=99%, iar transformatoare electrice cu h=99,8%, dar ele reprezinta rezultate de varf ale tehnicii actuale (este vorba de masini si transformatoare de puteri mari).
Pe de alta parte, descrierea cea nai exacta a proceselor de conversie a energiei in convertoare in regim stationar si cel dinamic, se realizeaza cu ajutorul ecuatiilor diferentiale de o anumita complexitate. Dar aceste ecuatii in general nu au o solutie daca rezistentele active, ce figureaza in aceste ecuatii drept coeficienti ai unor termeni, devin nule sau se neglijeaza. De aici rezulta ca un convertor real trebuie sa posede astfel de elemente care au proprietatile unui rezistor, respectiv conversia energiei nu se poate realiza fara o componenta termica, care apare in cadrul oricarui element de circuit cu proprietatile unui rezistor si deci randamentul conversiei nu poate fi decat subunitar.
Pentru ca in masina electrica sa nu apara componenta termica este necesar ca ea sa nu posede fier, , respectiv sa posede infasurari supraconductoare si sa nu se produca pierderi mecanice. Un astfel de sistem electrotehnic este posibil, dar el nu va fi un convertor, ci un acumulator de energie.
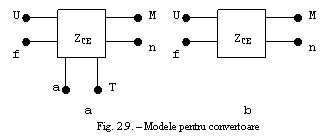 Asa cum s-a mentionat deja un convertor poate fi
prezentat ca un hexapol cu doua borne 'electrice'
corespunzatoare tensiunii U si frecventei f (figura 2,9 a)
doua borne 'mecanice' corespunzatoare momentului cuplului
electromagnetic M si turatiei n si doua borne
'termice' corespunzatoare cantitatii de
caldura Q si temperaturii T. Dar in majoritatea cercetarilor
conturul termic corespunzator convertorului este considerat cu un volum
infinit si temperatura constanta, ceea ce permite reprezentarea acestuia
printr-un cvadripol cu impedanta interna ZCE, asa cum se
arata in figura 9.b. Cand procesele legate de conversia energiei din
interiorul convertorului nu au o importanta deosebita, atunci
convertorul poate fi prezentat ca un cvadripol dar cu ZCE=0
Asa cum s-a mentionat deja un convertor poate fi
prezentat ca un hexapol cu doua borne 'electrice'
corespunzatoare tensiunii U si frecventei f (figura 2,9 a)
doua borne 'mecanice' corespunzatoare momentului cuplului
electromagnetic M si turatiei n si doua borne
'termice' corespunzatoare cantitatii de
caldura Q si temperaturii T. Dar in majoritatea cercetarilor
conturul termic corespunzator convertorului este considerat cu un volum
infinit si temperatura constanta, ceea ce permite reprezentarea acestuia
printr-un cvadripol cu impedanta interna ZCE, asa cum se
arata in figura 9.b. Cand procesele legate de conversia energiei din
interiorul convertorului nu au o importanta deosebita, atunci
convertorul poate fi prezentat ca un cvadripol dar cu ZCE=0
A DOUA LEGE: toate masinile electrice sunt reversibile, adica ele pot lucra atat in regimul de motor cat si in regimul de generator.
Faptul ca unul si acelasi convertor electromecanic poate lucra atat in regim de motor cat si in regim de generator reprezinta un mare avantaj al acestui tip de convertor in raport cu alte tipuri (masini de abur, diesel, motoare reactive etc ). Regimul de lucru al masinii electrice depinde de momentul static rezistent aplicat la arborele sau.
Daca energia electrica este preluata din reteaua de alimentare atunci masina se gaseste in regim de motor (vezi fig. 8. a), iar daca, dimpotriva, este preluata energia mecanica la arborele masinii atunci ea se gaseste in regim de generator.
Pe de alta parte, la masini electrice de tip inductiv infasurarile statorice si rotorice se 'cupleaza' intre ele cu ajutorul campului magnetic. Si pentru ca sa se realizeze 'legatura' dintre o infasurare mobila (aflata in miscare de rotatie) si una imobila strabatut de c.a. sau c.c., este necesar ca in intrefierul masinii sa se formeze un camp magnetic invartitor (rotitor). Pentru a obtine un astfel de camp in cazul c.c. este necesar sa fie rotita infasurarea parcursa de c.c. (producerea campului magnetic invartitor pe cale mecanica). Daca insa infasurarea este fixa, atunci printr-o dispunere adecvata in spatiu a infasurarii (decalaj spatial) si printr-o defazare in timp adecvata a curentilor ce parcurg infasurarea se poate obtine, de asemenea, in intrefierul masinii un camp magnetic invartitor (producerea campului invartitor pe cale electrica).
Pentru producerea campului magnetic la masinile de c.a. este necesara puterea reactiva.
Astfel, de fapt in infasurarile masinii de c.a. circula curentii activi si reactivi (mai precis un curent cu o componenta activa, respectiv reactiva) ; curentii reactivi produc campul magnetic invartitor din intrefierul masinii, iar curentii activi produc puterea activa a masinii. In regimul stabilizat al masinii puterea reactiva poate 'intra' in masina pe la stator, sau pe la rotor, sau pe la stator si rotor, iar sensul energiilor reactive si active din masina nu depind de regimul masinii (motor sau generator) si in general pot avea acelasi sens sau sensuri inverse. Aceasta inseamna ca energia activa poate proveni de la stator, iar cea reactiva de la rotor sau invers.
In principiu puterea activa din masina isi schimba sensul in functie de regimul de motor sau generator al masinii, in timp ce fluxul energiei termice nu-si schimba sensul. Pierderile din convertor sunt ireversibile, dar formele constructive ale convertoarelor sunt atat de numeroase incat exista si convertoare care realizeaza conversia energiei termice in cea electrica sau mecanica. Principiul de functionare a unor astfel de convertor se bazeaza pe modificarea permeabilitatii magnetice, respectiv permitivitatii electrice a materialelor in care este concentrata energia campului magnetic sau electric. In acest caz insa modificarea temperaturii trebuie sa produca in apropierea punctului Curie
A TREIA LEGE: conversia
electromecanica a energiei se realizeaza cu ajutorul campurilor, care
apar imobile unul in raport cu altul. ![]()
![]()
![]()
Campul magnetic statoric si cel retoric, care apar imobile unul in raport cu altul, produc in intrefierul masinii un camp rezultant .si momentul cuplului electromagnetic
![]() (1.)
(1.)
in care W este viteza unghiulara a campului, iar P este puterea electromagnetica, adica puterea campului magnetic concentrata in intrefierul masinii. infasurarile masinilor electrice se executa astfel incat in intrefierul masinii sa se produca camp magnetic invartitor circular, care contine o singura armonica (cea fundamentala) ; un astfel de camp se numeste sinusoidal.
Pe de alta parte, campul magnetic invartitor poate fi creat cu ajutorul unui sistem bifazat de curenti (deci curenti defazati intre ei in timp cup/2) care parcurg doua infasurari decalate intre ele p/2, sau cu ajutorul unui sistem trifazat de curenti (deci curenti defazati intre ei in timp cu 2p/3 rad.) care parcurg un sistem trifazat de infasurari decalate intre ele cu 2p/3 rad., iar in cazul general poate fi realizat de un sistem m-fazat de curenti (defazati intre ei cu 2 p/m rad.), care circula prin m infasurari decalate intre ele cu 2p /m rad.
Campul magnetic invartitor se poate obtine si cu ajutorul c.c. dar atunci infasurarea prin care circula c.c. trebuie sa se roteasca cu o anumita viteza unghiulara. La o masina sincrona, in majoritatea cazurilor, campul magnetic invartitor se produce de catre infasurarea statorica si viteza sa unghiulara (uneori se noteaza W sau Ws ) este denumita viteza de sincronism. Rotorul masinii sincrone are aceeasi viteza W W si de aceea frecventa marimilor electrice din rotorul masinii este f2 = 0, respectiv in rotorul acestei masini avem c.c.
La masina de c.c. infasurarea de excitatie este montata in stator si este alimentata in c.c., deci campul sau este imobil, in schimb in rotorul masinii de c.c. se realizeaza camp magnetic invartitor a carui viteza este aceeasi cu a rotorului dar de sens invers, astfel incat cele doua campuri ale masinii -statoric si rotoric - apar imobile unul in raport cu altul.
La
masina asincrona frecventa curentului din rotor este:![]()
![]()
f2=sf1 (.2)
in care s este asa-numita alunecare a masinii definita prin relatia:
![]()
![]() , (3)
, (3)
iar ![]() este frecventa
marimilor din statorul masinii. De aceea suma dintre viteza rotorului
masinii si viteza relativa (in raport cu rotorul) a campului
rotoric este egala cu W - adica, de asemenea,
cele doua campuri magnetice (statoric si rotoric) apar ca fiind
imobile unul fata de altul.
este frecventa
marimilor din statorul masinii. De aceea suma dintre viteza rotorului
masinii si viteza relativa (in raport cu rotorul) a campului
rotoric este egala cu W - adica, de asemenea,
cele doua campuri magnetice (statoric si rotoric) apar ca fiind
imobile unul fata de altul.
La transformatoare electrice infasurarile sunt fixe astfel incat frecventele sunt identice in infasurari. De aici rezulta ca fluxul magnetic se 'deplaseaza' in lungul coloanelor miezului magnetic cu aceeasi frecventa in raport cu infasurarea primara si secundara, dar la transformatoare are o semnificatie mai mica imobilitatea campurilor magnetice ale celor doua infasurari.
In
general insa, la masini electrice are loc o rezonanta de
tip electromecanic cand frecventa ![]() a retelei de
alimentare si turatia n a masinii (in ture/s) se
'leaga' intre ele prin relatia:
a retelei de
alimentare si turatia n a masinii (in ture/s) se
'leaga' intre ele prin relatia:
f1 = pn (.4)
in care p este numarul perechilor de poli ai masinii. Din (4) rezulta ca intr-o masina electrica multipolara, viteza de sincronism si cea mecanica sunt de p ori mai mici decat intr-o masina bipolara (cand p = 1).
La masinile electrice de tip inductiv- capacitiv si capacitiv, imobilitatea campurilor unul in raport cu altul nu are o semnificatie atat de mare ca in cazul unei masini de tip inductiv, avand in vedere ca masinile de tip inductiv-capacitiv, respectiv capacitiv,se prezinta mai ales sub forma de concentratori de energie la care apare rezonanta de tip electromecanic.
4. MASINA ELECTRICA - CONVERTOR ELECTROMECANIC AL ENERGIEI
A. - Introducere
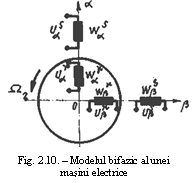 Rolul convertorului electromecanic de energie este acela de a
convertii energie electromagneticǎ in energie mecǎnicǎ sau
invers si de aceia ele trebuie sǎ posede unele "elemente" care
sǎ fie capabile sǎ producǎ transformarea respectivǎ.
La o masinǎ electricǎ rotativǎ "elementele" mentionate
trebuie sǎ producǎ un cuplu electromagnetic, care este
legat de producerea unui camp magnetic invartitor in
masinǎ. De aceia masinile electrice sunt formate dintr-o
anumitǎ combinatie spatiala a unor infasurari prin care
circula curenti cu anumite defazaje in timp. De fapt prin
aceasta se urmareste obtinerea unor campuri magnetice circulare
rotitoare care se pot realiza in cadrul unei masini bifazice in care
infasurarile sunt decalata la 90 , respectiv in cadrul unei
masini trifazice la care infasurarile sunt decalate la 120 Dar schema cea mai
simpla de masina electrica este cea de masina
bifazica - fig. 10. In aceasta figura
infasurarile statorice
Rolul convertorului electromecanic de energie este acela de a
convertii energie electromagneticǎ in energie mecǎnicǎ sau
invers si de aceia ele trebuie sǎ posede unele "elemente" care
sǎ fie capabile sǎ producǎ transformarea respectivǎ.
La o masinǎ electricǎ rotativǎ "elementele" mentionate
trebuie sǎ producǎ un cuplu electromagnetic, care este
legat de producerea unui camp magnetic invartitor in
masinǎ. De aceia masinile electrice sunt formate dintr-o
anumitǎ combinatie spatiala a unor infasurari prin care
circula curenti cu anumite defazaje in timp. De fapt prin
aceasta se urmareste obtinerea unor campuri magnetice circulare
rotitoare care se pot realiza in cadrul unei masini bifazice in care
infasurarile sunt decalata la 90 , respectiv in cadrul unei
masini trifazice la care infasurarile sunt decalate la 120 Dar schema cea mai
simpla de masina electrica este cea de masina
bifazica - fig. 10. In aceasta figura
infasurarile statorice![]() sunt decalate in spatiu
si in campul magnetic cu 90 , similar si infasurarile rotorice
sunt decalate in spatiu
si in campul magnetic cu 90 , similar si infasurarile rotorice![]() . Pentru ca in intrefierul masinii bifazice sa se produca un camp magnetic
invartitor este necesar ca infasurarile statorice sau cele
rotorice sa fie alimentare cu tensiuni defazate (in timp) cu 90 , sau sa fie strabatute de curenti
defazati (in timp) intre ei cu 90
. Pentru ca in intrefierul masinii bifazice sa se produca un camp magnetic
invartitor este necesar ca infasurarile statorice sau cele
rotorice sa fie alimentare cu tensiuni defazate (in timp) cu 90 , sau sa fie strabatute de curenti
defazati (in timp) intre ei cu 90
Conform cu a treia lege a electromecanicii, conversia energiei va fi posibilǎ intr-un astfel de sistem dacǎ se va respecta urmǎtoarea relatie a vitezelor unghiulare:
![]() (5)
(5)
in care cu Wr s-a notat viteza unghiularǎ relativǎ a campului magnetic rotoric in raport cu rotorul. In acest caz campurile magnetice ale rotorului si statorului apar imobile unul fatǎ de altul. O datǎ cu modificarea lui W sau W se modificǎ frecventa curentului rotoric (vezi (2) si (3)) dar campurile rǎman imobile unul in raport cu altul. In principiu campurile trebuie sǎ fie rotitoare, dar circulare si nu de alt tip (de exemplu,de tip eliptic).
Pe de alta parte, campul magnetic din intrefierul masinii va fi circular numai daca:
- tensiunile din infǎsurǎri (statorice si rotorice) sunt sinusoidale;
- masina electricǎ este idealǎ.
Prin masina electrica ideala se intelege acea masina la care:
1 - intrefierul este uniform si neted (masina nu poseda crestaturi in stator si in rotor);
2 - infasurarile masinii sunt realizate sub forma unei pelicule (strat) de curent cu ajutorul careia se produce o distributie sinusoidala a fortei magnetomotoare in intrefier;
3 - permeabilitatea magnetica a fierului (miezului) masinii se considera infinitǎ (adicǎ nu se produce saturatia magneticǎ a fierului);
4 - masina este simetrica, adica infasurarile sale, circuitul sau magnetic, intrefierul sau sunt simetrice in raport cu axele de coordonate a si b
5 - curbura .intrefierului nu se ia in considerare.
Intr-o masina reala, majoritatea conditiilor prezentate anterior nu sunt indeplinite si atunci in intrefierul sau avem un spectru infinit de armonici ale campului magnetic. Armonicile superioare ale campului au o influenta complexa asupra procesului conversiei energiei pe calea electromecanica, de aceea initial se va prezenta functionarea masinii in prezenta armonicii fundamentale a campului magnetic, urmand ca unele efecte ale armonicilor superioare sǎ fie prezentate pe parcurs.
Masina electricǎ bifazicǎ cu schema din figura 10 se numeste masinǎ electricǎ generalizatǎ (prescurtat MEG) avand in vedere faptul cǎ la aceastǎ masinǎ se pot "reduce" procesele conversiei energiei de la toate celelalte tipuri de bazǎ ale masinilor. Descrierea conversiei energiei in cadrul masinii electrice generalizate se face cu ajutorul unor ecuatii diferentiale adecvate si ele sunt patru in acest caz, in timp ce pentru oricare alt tip de masina numarul lor este mai mare; de fapt acesta este avantajul principal al 'reducerii' celorlalte masini la o masina electrica generalizata.
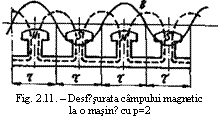 Pentru doi pasi polari 2t (pasul polar t este portiunea din desfasurata sistemului magnetic
al masinii corespunzatoare unui pol) se produce o
variatie completa a inductiei magnetice B, respectiv ceea ce
se petrece, din punctul de vedere
al campului magnetic, sub o pereche de poli magnetici, se
regaseste sub oricare alta pereche de poli. De aceea la o masina simetrica
se poate calcula t.e.m., puterea si alti parametri, in zona
corespunzatoare unei singure perechi de poli, dupa care recalcularea
parametrilor se face tinand seama de numarul perechilor de poli p ai
masinii.
Pentru doi pasi polari 2t (pasul polar t este portiunea din desfasurata sistemului magnetic
al masinii corespunzatoare unui pol) se produce o
variatie completa a inductiei magnetice B, respectiv ceea ce
se petrece, din punctul de vedere
al campului magnetic, sub o pereche de poli magnetici, se
regaseste sub oricare alta pereche de poli. De aceea la o masina simetrica
se poate calcula t.e.m., puterea si alti parametri, in zona
corespunzatoare unei singure perechi de poli, dupa care recalcularea
parametrilor se face tinand seama de numarul perechilor de poli p ai
masinii.
La o masina multipolara, viteza de sincronism este de p ori mai mica decat la o masina bipolara
![]() (6)
(6)
iar daca se tine seama ca frecventa standard este f = 5o Hz, atunci se poate alcatui urmatorul tabel pentru turatiile de sincronism n. in functie de numarul perechilor de poli p, determinate cu relatia (6)
![]()
tabelul 1
|
Numǎrul perechilor de poli p | |||||||
|
Turatia de sincronism n1 [ture/min] |
La studiul masinilor electrice se foloseste
notiunea de unghi electric ![]() definit prin relatia:
definit prin relatia:
ae=pag (7)
in care ag reprezinta unghiul geometric. Notiunea de unghi
electric este foarte utilǎ mai ales in cazul masinilor electrice
multipolare. Astfel, la o masina electrica cu p = 2 daca
vrem sa aflam care este valoarea inductiei magnetice (care variaza
armonic in intrefierul masinii) la "distanta" unghiulara ![]() de punctul de referinta, atunci trebuie sa
scriem:
de punctul de referinta, atunci trebuie sa
scriem:
![]()
avand in vedere ca o variatie sinusoidala (in acest caz) completa se produce pe distanta unghiularǎ corespunzǎtoare lui 2t, iar t poate fi definitǎ prin relatia:
![]() (8.)
(8.)
in care D, R reprezinta diametrul, respectiv raza statorului (rotorului) masinii.
B. - Reducerea tipurilor de masini clasice la MEG
B1. Asa cum s-a amintit
deja tipurile de baza ale masinilor electrice pot fi reduse la
masina electrica generalizata, care in principiu este
formata (fig.l0) din doua perechi de infasurari ce se
deplaseaza unele in raport cu altele. Astfel, masina
asincrona (nesincrona) se obtine din masina
electrica generalizata (MEG) cand infasurarile
statorice ![]() se alimenteaza cu
tensiuni sinusoidale cu frecventa
se alimenteaza cu
tensiuni sinusoidale cu frecventa ![]() defazate intre ele cu 90 . In acest caz, in
infasurarile rotorice avem curenti cu frecventa f2
= sf1, care se obtin cu ajutorul tensiunilor aplicate infasurarilor
sau se induc cu ajutorul infasurarilor statorice. La masina
asincrona W W
defazate intre ele cu 90 . In acest caz, in
infasurarile rotorice avem curenti cu frecventa f2
= sf1, care se obtin cu ajutorul tensiunilor aplicate infasurarilor
sau se induc cu ajutorul infasurarilor statorice. La masina
asincrona W W
B Masina sincrona poate fi obtinuta, de asemenea, din (MEG) daca infasurarile statorice se alimenteaza cu tensiuni alternative (ca si la masina asincrona), iar infasurarile rotorice cu tensiuni continue sau invers. In acest caz W W , adicǎ campurile statorice si rotorice sunt imobile unul in raport cu altul. Daca tensiunea continua se aplica infasurarilor statorice, atunci campul rotoric se roteste in sens invers rotirii rotorului si cu aceeasi viteza cu acesta, astfel incat totusi campurile (statoric si rotoric) raman imobile unul in raport cu altul.
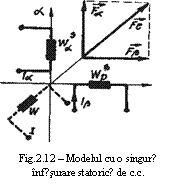
B3. In cazul in care insa infasurarile (statorica sau retorica) se alimenteaza in c.c., este de fapt suficient sa existe o singura infasurare, care produce o forta magnetomotoare (f.m.m.) egala cu rezultanta fortelor (f.m.m.) produse de fiecare infasurare in parte - figura 1
![]() (9)
(9)
Executand o singura
infasurare ![]() (denumita infasurare de excitatie)
in loc de doua
(denumita infasurare de excitatie)
in loc de doua ![]() se obtine o
economie de cupru avand in vedere cǎ in acest caz nu vor fi necesare decat
1,4 unitati de cupru in loc de 2 unitati (de exemplu, daca
se obtine o
economie de cupru avand in vedere cǎ in acest caz nu vor fi necesare decat
1,4 unitati de cupru in loc de 2 unitati (de exemplu, daca
![]() ).
).
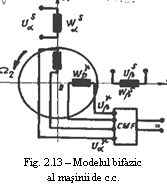
 La masina de c.c. in infasurarea rotorica
circula un curent multifazat, care se
obtine cu ajutorul colectorului (ce poate fi privit ca un convertor
mecanic de frecventa (CMF)) din c.c., iar daca se
realizeaza reducerea sistemului
multifazat la unul bifazat se obtine schema masinii de c.c. in cadrul
acestui sistem din urma -figura 13. Ca si la o masina
sincrona campul magnetic rotoric se roteste in sens invers rotorului
si pentru W W campul rotoric apare imobil
in raport cu infasurarea de excitatie statorica si
sistemul de coordonate (a b). La masina de c.c. ca si la cea sincrona
alunecarea este nula. Colectorul masinii de c.c., care este un (CMF),
poate fi inlocuit cu un convertor de frecventa realizat cu elemente
semiconductoare. In aceasta situatie conversia energiei in
intrefierul masinii principial nu se modifica, dar in cazul colectorului
frecventa f2 este legata rigid de W , iar in cazul unui (CMF) cu
semiconductoare se poate realiza o conexiune inversa flexibila intre
f2 si W Tipul acesta din urmǎ de masina se numeste masinǎ
cu ventile (dispozitivele cu semiconductoare au proprietati de
ventil), sau masina cu comutator cu ventile, masini de
c.c. fara contacte etc.
La masina de c.c. in infasurarea rotorica
circula un curent multifazat, care se
obtine cu ajutorul colectorului (ce poate fi privit ca un convertor
mecanic de frecventa (CMF)) din c.c., iar daca se
realizeaza reducerea sistemului
multifazat la unul bifazat se obtine schema masinii de c.c. in cadrul
acestui sistem din urma -figura 13. Ca si la o masina
sincrona campul magnetic rotoric se roteste in sens invers rotorului
si pentru W W campul rotoric apare imobil
in raport cu infasurarea de excitatie statorica si
sistemul de coordonate (a b). La masina de c.c. ca si la cea sincrona
alunecarea este nula. Colectorul masinii de c.c., care este un (CMF),
poate fi inlocuit cu un convertor de frecventa realizat cu elemente
semiconductoare. In aceasta situatie conversia energiei in
intrefierul masinii principial nu se modifica, dar in cazul colectorului
frecventa f2 este legata rigid de W , iar in cazul unui (CMF) cu
semiconductoare se poate realiza o conexiune inversa flexibila intre
f2 si W Tipul acesta din urmǎ de masina se numeste masinǎ
cu ventile (dispozitivele cu semiconductoare au proprietati de
ventil), sau masina cu comutator cu ventile, masini de
c.c. fara contacte etc.
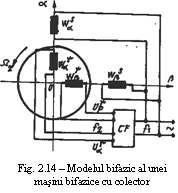
B4. La masini de c.a" cu colector atat in stator cat si in rotor avem c.a., iar convertorul de frecventa converteste c.a. de frecventa standard intr-un c.a. de frecventa corespunzatoare alunecarii masinii (frecventa de alunecare) - figura 14. Ca si la toate celelalte masini campurile statoric si rotoric apar imobile unul fata de altul. Tipul acesta de masini por fi monofazate sau trifazate, iar infasurarile statorice si rotorice se pot conecta in serie sau in paralel sau sa fie cuplate magnetic.
Convertorul de frecventa (CF) in cazul alimentarii de la c.a. lucreaza in conditii mai grele decat in cazul in care se realizeaza convertirea c.c. in c.a. Asta se reflecta mal ales intr-o scanteiere mai pronuntata a periilor la colector.
B5. Plecand de la (MEG) pentru W = 0 se obtine de fapt convertorul electromagnetic - adica transformatorul electric. In acest caz este suficient sa fie luata in considerare o infasurare statorica si una rotorica, de exemplu corespunzatoare axei a sau b, avand in vedere ca la W = 0 cuplajul magnetic cu cealalta pereche de infasurari este nul. (infasurarile sunt decalate spatial cu 90°). Desi la transformatoare avem doar o conversie electromagnetica a energiei, totusi ele sunt incluse in capitolele de "masini electrice" pentru ca functionarea lor decurge din acelasi sistem de ecuatii, iar tehnologia lor de executie este apropiata de cea a masinilor electrice propriu-zise. In cazul transformatoarelor, puterea activa se poate transfera din infasurarea primara in cea secundara sau invers, iar puterea reactivǎ poate provenii de la infǎsurarea primarǎ sau cea secundarǎ.
C. Formarea momentului cuplului electromagnetic
In ceea ce priveste formarea momentului electromagnetic al masinilor electrice se poate lua in considerare cazul cand in infasurarile (MEG) avem c.c. Momentul electromagnetic rotitor se produce cu ajutorul curentilor ce parcurg infasurarile statorice si rotorice dupa axele a si b
![]() (10)
(10)
in care LM este inductivitatea mutuala dintre infasurarile statorice si rotorice.
Produsele
curentilor de tipul ![]() la o masinǎ
simetricǎ nu produc un moment invartitor, ci produc doar vibratii
si eforturi (forte) dupǎ anumite directii.
la o masinǎ
simetricǎ nu produc un moment invartitor, ci produc doar vibratii
si eforturi (forte) dupǎ anumite directii.
Daca in infasurarile statorice si rotorice ale unei (MEG) avem numai c.c. atunci este posibil sa inceapa rotirea masinii (pana ajunge,de exemplu, axa unui pol S rotoric in dreptul unei axe N statoric), dar intr-o faza urmatoare masina se va opri, infasurarile fiind intr-o pozitie oarecare neutrala. De aceea in infasurari trebuie sa avem c.a. sau in una dintre infasurari (statorica sau retorica) c.c., iar in cealalta (rotorica sau statorica) c.a.
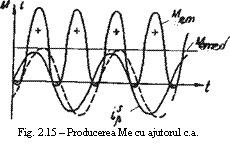 Formarea momentului electromagnetic invartitor, in cazul folosirii
curentilor alternativi, este aratata in fig, 15. Produsul
curentilor nu-si schimba semnul cand curentii statoric
si rotoric isi schimba semnul, decat in cazul in care
curentii respectivi sunt si defazati intre ei - figura 15. In
cazul defazajului dintre curentii mentionati, deci in cazul
existentei componentei reactive, apare componenta constanta (valoarea
medie Mm ) a momentului electromagnetic
care depinde de defazajul curentilor din stator si rotor.
Formarea momentului electromagnetic invartitor, in cazul folosirii
curentilor alternativi, este aratata in fig, 15. Produsul
curentilor nu-si schimba semnul cand curentii statoric
si rotoric isi schimba semnul, decat in cazul in care
curentii respectivi sunt si defazati intre ei - figura 15. In
cazul defazajului dintre curentii mentionati, deci in cazul
existentei componentei reactive, apare componenta constanta (valoarea
medie Mm ) a momentului electromagnetic
care depinde de defazajul curentilor din stator si rotor.
Momentul electromagnetic poate fi determinat si prin produsul fluxurilor magnetice, respectiv prin produsi curentilor si al fluxurilor magnetice avand in vedere ca intre fluxurile magnetice si curentii care ii produc exista relatii cunoscute (de tipul L =ψ/i).
Pentru determinarea momentului electromagnetic al unei masini simetrice multifazate cu m faze - se face raportarea acesteia la una bifazicǎ.
![]() (11)
(11)
Din cele prezentate anterior, rezulta ca desi apar deosebiri nete in constructia si alimentarea masinilor electrice, ele au totusi o proprietate comuna: sunt convertoare electromecanice de energie.
5. CAMPURILE MAGNETICE ALE TRANSFORMATOARELOR SI MASINILOR ELECTRICE
Conversia electromagneticǎ a energiei se realizeazǎ in intrefierul masinii electrice - adica in spatiul unde este concentrata energia (cea mai mare parte) a campului magnetic. De aceea studiul campurilor magnetice ale masinii are o importanta deosebita pentru descifrarea proceselor de conversie a energiei in masinile electrice.
Pe de alta parte, pe diferite portiuni ale circuitelor magnetice ale transformatoarelor si masinilor electrice, campul magnetic poate fi constant sau, variabil in timp si in spatiu, iar in intrefierul masinilor electrice el poate fi unipolar sau heteropolar. In continuare se prezintǎ aceste variante de camp magnetic.
5.1. CAMP MAGNETIC UNIPOLAR
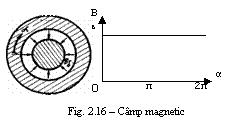 Campul magnetic unipolar
este specific masinilor unipolare care poseda o infasurare
de excitatie alimentata in c.c. Acest camp este constant in timp
si in spatiu. In intrefierul masinii liniile campului magnetic
sunt dirijate dupa raza - este vorba deci de un camp radial. In
figura 16 sunt reprezentate liniile campului magnetic in intrefierul
masinii (mult marit) si reprezentarea grafica a
inductiei din intrefier Bδ in functie de coordonata
unghiularǎ α.In cazul in care infasurarea de excitatie
a masinii este alimentata in c.a.,atunci inductia
Campul magnetic unipolar
este specific masinilor unipolare care poseda o infasurare
de excitatie alimentata in c.c. Acest camp este constant in timp
si in spatiu. In intrefierul masinii liniile campului magnetic
sunt dirijate dupa raza - este vorba deci de un camp radial. In
figura 16 sunt reprezentate liniile campului magnetic in intrefierul
masinii (mult marit) si reprezentarea grafica a
inductiei din intrefier Bδ in functie de coordonata
unghiularǎ α.In cazul in care infasurarea de excitatie
a masinii este alimentata in c.a.,atunci inductia ![]() este variabila in timp exact dupa aceeasi lege
ca si c.a. ( nu apar defazaje intre
este variabila in timp exact dupa aceeasi lege
ca si c.a. ( nu apar defazaje intre ![]() si
c.a.).Daca masina are si intrfierul variabil , atunci
si
c.a.).Daca masina are si intrfierul variabil , atunci ![]() este o functie de timp si de coordonata
unghiulara (spatiala)
este o functie de timp si de coordonata
unghiulara (spatiala) ![]() .
.
5. CAMP MAGNETIC HETEROPOLAR
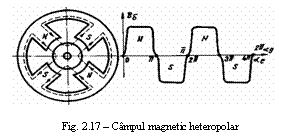
Campul magnetic heteropolar este specific unei masini electrice cu p ≥ 2 si cu poli aparenti formati din magneti permanenti sau electromagneti cu infasurarea de excitatie alimentata in c.c. Un exemplu de o astfel de masina cu p=2 este data in figura 17. Tot in aceasta figura este data variatia campului magnetic din intrefierul masinii Bδ cu precizarea ca acest camp este aproape constant in dreptul polilor (liniile de camp au directie radiala), iar in zona dintre poli Bδ are o valoare redusa avand in vedere ca intrefierul este mult marit si reluctanta magnetica are si ea valoare mare. Din graficul lui Bδ se poate observa, de asemenea, ca inductia magnetica realizeaza o variatie completa pe o portiune egala cu jumatate (pentru cazul p=2) din desfasurarea totala (2π) a coordonatei unghiulare αg - adica se respecta relatia (7) mentionata anterior.
5.3. CAMP MAGNETIC ALTERNATIV
Campul magnetic cu variatie alternativa (caz particular cu variatie sinusoidala) in timp si aproape constant in spatiu, este specific unei infasurari formate din w spire, parcurse de c.a, i=Imsinωt si montata pe un miez de fier corespunzator unui circuit magnetic cu contur inchis ~ figura 18.
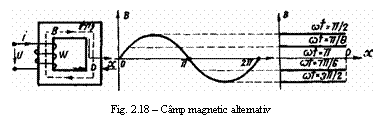 Daca se ia in considerare linia medie de camp in miezul de
fier cu lungimea l, atunci din aplicarea teoremei lui Ampere pe conturul inchis
(Γ) rezultǎ:
Daca se ia in considerare linia medie de camp in miezul de
fier cu lungimea l, atunci din aplicarea teoremei lui Ampere pe conturul inchis
(Γ) rezultǎ:
![]()
respectiv
![]()
iar relatia inductiei este:
![]() (12)
(12)
In figura 18 s-a reprezentat variatia inductiei magnetice in timp, respectiv in functie de coordonata x pentru mai multe momente de timp. Curentul si inductia rǎman in fazǎ.
5.4.CAMP MAGNETIC HETEROPOLAR ALTERNATIV
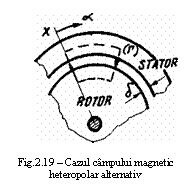 Tipul acesta de camp este specific unei masini
heteropolare si a carei infasurare de excitatie
este alimentata in c. a.
Tipul acesta de camp este specific unei masini
heteropolare si a carei infasurare de excitatie
este alimentata in c. a.
Sa admitem ca statorul masinii este format dintr-un miez statoric a carei infasurare este excitata (alimentata) in c. a., iar densitatea liniara (luata pe periferia interioara a statorului) a spirelor este wcosα , in care α este coordonata unghiulara luata in raport cu o axa de referinta - figura 19.
Daca se aplica teorema lui Ampere pe un contur inchis oarecare (Γ), rezulta:
![]()
respectiv
![]() (13)
(13)
in care s-a tinut seama cǎ portiunile din fier ale conturului (Γ) au tensiunile magnetice neglijabile in raport cu cele din intrefier. Dacǎ se are in vedere cǎ i este variabil in timp (i=Imsinωt) atunci (13) devine :
![]() (13.a)
(13.a)
in care
![]()
Expresia inductiei magnetice este:
![]() (14)
(14)
in care :
![]()
din care rezultǎ cǎ inductia din intrefier Bδ variazǎ in timp si in spatiu dupǎ o lege armonicǎ.
5.5. CAMP MAGNETIC INVARTITOR CIRCULAR
A. Introducere
 Campul magnetic invartitor circular
este una din cele mai importante notiuni din teoria masinilor si
el apare in intrefierul masinilor electrice heteropolare. Cu ajutorul
acestui camp se obtine momentul cuplului electromagnetic rotitor,
adica acela care la motoare electrice produce rotirea lor.
Campul magnetic invartitor circular
este una din cele mai importante notiuni din teoria masinilor si
el apare in intrefierul masinilor electrice heteropolare. Cu ajutorul
acestui camp se obtine momentul cuplului electromagnetic rotitor,
adica acela care la motoare electrice produce rotirea lor.
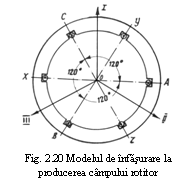
Avand in vedere importanta deosebita a campului magnetic invartitor se va realiza mai intai o prezentare mai intuitiva a acestuia, iar apoi se vor discuta si modalitatile de producere a acestuia. Astfel, ne propunem un miez feromagnetic statoric de masina trifazata; intreaga infasurare pe o faza statorica este insa concentrata intr-o pereche de crestaturi. Planurile crestaturilor in care sunt montate cele trei faze statorice sunt decalate intre ele spatial cu 1200 asa cum apare in figura 20. Perpendicular pe planul fazelor se definesc axele O-I; O- II; O- III, care formeaza desigur un sistem de axe decalate cu 1200 intre ele. Daca se alimenteaza infasurarea statorica trifazata cu un sistem trifazat simetric de curenti:
![]() ;
; ![]() ;
; ![]() ,
,
atunci fiecare infasurare monofazica va produce un camp magnetic al carui sens si directie (dat de regula burghiului drept) va fi cel dupa axele definite anterior, iar inductiile respective vor fi in faza cu curentii care au produs campul respectiv:
![]() ;
; ![]() ;
; ![]() . (15)
. (15)
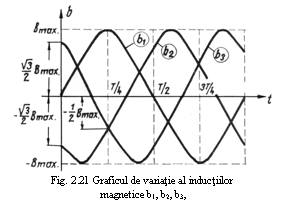
Graficul variatiei in timp a acestor inductii considerand campul fazei (A-X) ca fiind cel de referinta, este dat in figura 21. Dar important este campul rezultant din intrefierul masinii, respectiv inductia rezultanta. Pentru aceasta se vor compune inductiile magnetice, pentru diferite momente de timp, tinand seama de directiile si sensurile acestora. Astfel, din graficul inductiilor (fig. 21) rezulta ca la momentul t=0, avem:
![]() ;
; ![]() ;
; ![]() .
.
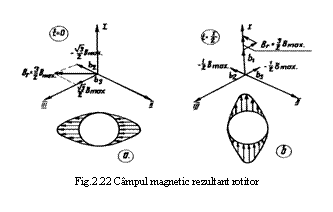
Compunand aceste valori ale inductiilor in sistemul O-I-II-III se obtine reprezentarea din figura 22a.
Unele calcule simple arata ca inductia
rezultanta este ![]() , directia ei este perpendiculara pe axa 0-I, iar
sensul sau este cel ce se obtine prin decalare cu
, directia ei este perpendiculara pe axa 0-I, iar
sensul sau este cel ce se obtine prin decalare cu ![]() in urma axei 0-I. In partea inferioara a figurii 22 a
este redata mai sugestiv variatia inductiei magnetice rezultante
(pe periferia interioara a statorului, respectiv in intrefierul
masinii) cu maximul sau orientat dupa directia si
sensul mentionate La momentul t = T/4, inductiile dupa cele trei
directii au valorile (fig. 21):
in urma axei 0-I. In partea inferioara a figurii 22 a
este redata mai sugestiv variatia inductiei magnetice rezultante
(pe periferia interioara a statorului, respectiv in intrefierul
masinii) cu maximul sau orientat dupa directia si
sensul mentionate La momentul t = T/4, inductiile dupa cele trei
directii au valorile (fig. 21):
![]() ;
; ![]() ;
; ![]() .
.
Inductia
rezultanta are aceeasi valoare ![]() ca si in momentul precedent numai ca directia
si sensul sau sunt data de axa 0-I.
ca si in momentul precedent numai ca directia
si sensul sau sunt data de axa 0-I.
Luand in considerare si momentele t = T/2; t = 3T/4; t= T, se ajunge la urmatoarele concluzii:
a) valoarea inductiei rezultante nu se modifica in timp;
b) cu fiecare interval de timp Δt = T/4, maximul inductiei se
roteste cu ![]() radiani.
radiani.
Aceasta ultima observatie a dus la denumirea de camp magnetic invartitor acestui tip de camp magnetic. Denumirea aceasta este totusi improprie pentru ca, un camp magnetic (ca de altfel orice fel de camp) nu are proprietati 'de invartire' asa cum au corpurile, de exemplu. De fapt, ceea ce 'se invarteste' este maximul inductiei magnetice a campului magnetic rezultant obtinut in intrefierul masinii. Intr-adevar, maximul acesta 'se roteste' in intrefier cu turatia ns=l/T=f[rot/s]. Aceasta este turatia campului magnetic invartitor in cazul in care cu infasurarea fiecarei faze statorice se realizeaza o pereche de poli. Daca se obtin insa p perechi de poli magnetici, atunci la o variatie completa a inductiei magnetice se parcurge doar 1/p din perimetrul statoric al masinii si deci in cazul general avem
![]() (16)
(16)
Regasim astfel relatia (6) corespunzatoare turatiei de sincronism a unei masini heteropolare. Asadar, turatia de sincronism nu este decat turatia campului magnetic invartitor.
In practica, campul magnetic invartitor se produce pe doua cai: calea mecanica si calea electrica.
B. Producerea campului magnetic invartitor pe calea mecanica.
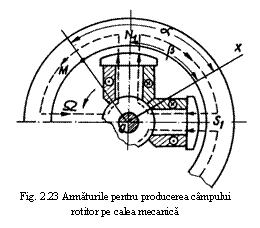 Se considera o armatura
rotorica cu poli aparenti (p =
2) care se roteste intr-un sens dat cu viteza unghiulara Ω -
figura Fiecare pol rotoric
poseda o infasurare, iar toate aceste infasurari
sunt legate intre ele in serie formand infasurarea rotorica
ce se alimenteaza de la o sursa de c.c, (specific masinii
sincrone). In acest fel polii rotorici produc un camp magnetic al carei
linii de camp trec prin armatura rotorica, prin intrefierul
masinii si prin armatura statorica In acest fel,
distributia campului magnetic in intrefierul masinii este de tipul
'dreptunghiular' ca in figura 17, dar ea poate fi aproximata
printr-o curba armonica (variatia dreptunghiulara se
descompune intr-o serie Fourier si se retine numai armonica
fundamentala). Astfel, intr-un punct M dispus pe periferia interioara
a statorului (deci in intrefierul masinii) inductia magnetica
poate fi notata sub forma
Se considera o armatura
rotorica cu poli aparenti (p =
2) care se roteste intr-un sens dat cu viteza unghiulara Ω -
figura Fiecare pol rotoric
poseda o infasurare, iar toate aceste infasurari
sunt legate intre ele in serie formand infasurarea rotorica
ce se alimenteaza de la o sursa de c.c, (specific masinii
sincrone). In acest fel polii rotorici produc un camp magnetic al carei
linii de camp trec prin armatura rotorica, prin intrefierul
masinii si prin armatura statorica In acest fel,
distributia campului magnetic in intrefierul masinii este de tipul
'dreptunghiular' ca in figura 17, dar ea poate fi aproximata
printr-o curba armonica (variatia dreptunghiulara se
descompune intr-o serie Fourier si se retine numai armonica
fundamentala). Astfel, intr-un punct M dispus pe periferia interioara
a statorului (deci in intrefierul masinii) inductia magnetica
poate fi notata sub forma
![]() , (17)
, (17)
in care α este unghiul pe care-l formeaza axa radiala OM a punctului considerat cu axa fixa OX, iar β este unghiul pe care il formeaza axa unui pol rotoric de exemplu, polul N1, la un moment dat t1, in raport cu aceeasi axa de referinta. Numai ca β este variabil in timp si expresia lui generala este:
![]() , (18)
, (18)
in care ![]() reprezinta un
unghi initial (ce poate fi luat egal cu zero, β 0= 0), de
aceea se poate nota:
reprezinta un
unghi initial (ce poate fi luat egal cu zero, β 0= 0), de
aceea se poate nota:
![]() (19)
(19)

Fig. 24 Graficele campului magnetic rotitor
Dupa (19), inductia punctelor din intrefierul masinii este functie de timp si de spatiu (α este un unghi spatial) si de fapt relatia (19) reprezinta expresia matematica pentru inductia campului magnetic invartitor al carui maxim se deplaseaza in intrefierul masinii cu viteza Ω (care este si viteza unghiulara a armaturii rotorice). In acest caz, deci campul magnetic invartitor se produce cu ajutorul unei armaturi rotorice, deci pe calea mecanica. In figura 24 se arata cum se deplaseaza maximul armonicii fundamentale a campului (momentele t1, t2, t3 etc.) mentionandu-se in abscisa atat unghiurile electrice cat si cele geometrice.
Referindu-ne la punctul M se pot lua in considerare cateva momente specifice:
![]() , deci cand punctul M
se afla in dreptul axei polului N1, atunci:
, deci cand punctul M
se afla in dreptul axei polului N1, atunci:
![]() si
si ![]() ;
;
![]() , deci punctul M se afla pe bisectoarea unghiului dintre
polii N1 si S1 (axa interpolara), atunci avem:
, deci punctul M se afla pe bisectoarea unghiului dintre
polii N1 si S1 (axa interpolara), atunci avem:
![]() ; (p si bM
; (p si bM
C. Producerea campului magnetic invartitor pe calea electrica
Vom lua in considerare o infasurare statorica polifazata cu m faze formata din m (cazul particular m = 3) infasurari electrice, distribuite pe periferia interioara a statorului astfel incat decalajul spatial dintre axele lor sa fie 2 π/mp (in grade geometrice). Sistemul infasurarilor cu m faze sunt parcurse de un sistem polifazat simetric de curenti:
![]() ;
;
![]() ;
;
(20)
![]() .
.
In ipoteza ca infasurarile fazelor sunt distribuite sinusoidal, intensitatea campului magnetic din intrefierul masinii rezulta din relatia (13a)
![]() ;
;
![]() ;
;
(21)
![]() .
.
in care
s-a notat ![]() . Pentru faza de indice k (k=1,2,...,m) intensitatea campului magnetic se poate nota sub forma
. Pentru faza de indice k (k=1,2,...,m) intensitatea campului magnetic se poate nota sub forma
![]() ,
,
si daca se tine seama de relatia trigonometrica
![]() ,
,
atunci avem:
![]() . (22)
. (22)
Intensitatea campului magnetic in intrefier este:
![]() , (23)
, (23)
in care s-a tinut seama de faptul ca
![]() .
.
Din (23) rezulta ca amplitudinea campului magnetic din intrefier este constanta si de m/2 ori mai mare decat amplitudinea produsa de o singura faza. Dar structura expresiei din (23) este identica cu cea din(19) deci este vorba de un camp magnetic invartitor - produs insa pe calea electrica. Daca se particularizeaza pentru m=2, se constata ca un camp magnetic invartitor poate fi produs si de o infasurare bifazica, specifica unei masini electrice generalizate. (MEG)
D. Unele proprietati ale campului magnetic invartitor
Campul magnetic invartitor are unele proprietati cu aplicare inginereasca directa.
a) Armonica fundamentala a
campului magnetic invartitor se suprapune perfect peste armonica
fundamentala a campului magnetic produs de o faza, atunci cand in
faza respectiva curentul ia valoarea maxima. Astfel, daca se
ia in considerare faza (A-X), curentul va avea valoarea maxima ![]() cand
cand ![]() , iar in aceasta situatie avem:
, iar in aceasta situatie avem:
![]() , respectiv
, respectiv ![]() .
.
Din aceste relatii rezulta ca, in acest caz, HA si H sunt in faza.
Daca
se ia in considerare faza (B-Y), atunci in aceasta faza valoarea maxima
a curentului ![]() , se obtine pentru
, se obtine pentru ![]() , iar in aceasta situatie avem:
, iar in aceasta situatie avem:
![]() , respectiv
, respectiv ![]() ,
,
din care rezulta in mod evident aceeasi concluzie.
b) Sensul de rotire a campului magnetic invartitor coincide cu sensul succesiunii fazelor montate pe periferia interioara a statorului si care produc campul. Aceasta proprietate rezulta din relatia
![]() , (24)
, (24)
adica
viteza campului magnetic invartitor are
sensul cresterii (semnul plus, care rezulta din aceea ca
raportul ![]() nu poate fi decat
pozitiv) coordonatei unghiulare
nu poate fi decat
pozitiv) coordonatei unghiulare ![]() , unghiul
, unghiul ![]() fiind considerat
intotdeauna in sensul succesiunii fazelor montate pe stator.
fiind considerat
intotdeauna in sensul succesiunii fazelor montate pe stator.
c) Din proprietatea precedenta rezulta imediat ca pentru inversarea sensului de rotire a campului magnetic invartitor, este suficienta inversarea succesiunii fazelor - adica, practic prin inversarea a, doua din cele trei legaturi ale retelei (trifazate) de alimentare la infasurarile de faza statorice.
5.6. CAMP MAGNETIC INVARTITOR ELIPTIC
Campul magnetic invartitor eliptic este specific masinilor electrice polifazate la care infasurarea polifazata nu este simetrica sau alimentarea ei nu se face cu un sistem de curenti polifati simetrici. Acelasi fenomen se produce si in cazul in care intrefierul masinii nu este uniform si variaza in timp datorita excentricitatii armaturii retorice in raport cu cea statorica.
In aceasta situatia se produce un camp magnetic invartitor cu o amplitudine variabila, fazorul campului descrie in planul complex o elipsa, iar viteza unghiulara variaza in functie de camp.
Ca exemplu, se ia in considerare o masina bifazica
in infasurarile decalate intre ele cu unghiul ![]() si care se parcurg de curenti
alternativi care au aceeasi frecventa dar amplitudini diferite,
respectiv sunt defazati intre ei cu unghiul
si care se parcurg de curenti
alternativi care au aceeasi frecventa dar amplitudini diferite,
respectiv sunt defazati intre ei cu unghiul ![]() . Intensitatile
campurilor magnetice produse de cele doua infasurari in
intrefierul masinii sunt:
. Intensitatile
campurilor magnetice produse de cele doua infasurari in
intrefierul masinii sunt:
![]() ;
;
![]() ,
,
respectiv:
![]() ;
;
![]() ,
,
iar campul magnetic rezultant este:
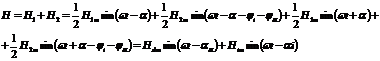
Cele
doua componente se pot compune in planul complex de coordonate (1,j), iar
daca se alege un alt sistem de coordonate (x,y) defazat de cel
initial cu unghiul![]() , atunci noile componente ale campului magnetic rezultant
devin
, atunci noile componente ale campului magnetic rezultant
devin
![]()
![]()
Prin eliminarea parametrului t din relatiile precedente rezulta:
![]() (25)
(25)
care
reprezinta ecuatia unei elipse cu semiaxa mare a = / Hd+Hi
/ si semiaxa mica b = / Hd-Hi / si
avand axele rotite cu unghiul ![]() in raport cu axele
planului complex initial. Sensul de rotire al fazorului
in raport cu axele
planului complex initial. Sensul de rotire al fazorului ![]() in planul complex este
in sensul undei invartitoare care are amplitudinea mai mare.
in planul complex este
in sensul undei invartitoare care are amplitudinea mai mare.
6. FORTELE MAGNETOMOTOARE SI UNELE FLUXURI MAGNETICE DIN MASINA ELECTRICA
A. Introducere
Daca Φ este fluxul magnetic fascicular (fluxul magnetic corespunzator unei sectiuni transversale a unui circuit feromagnetic), atunci fluxul magnetic total ce se inlantuie cu o infasurare cu w spire, montata pe miezul feromagnetic dat, se obtine prin relatia:
![]() , (26)
, (26)
iar inductivitatea infasurarii parcursa de curentul i (si cu ajutorul caruia se produce fluxul Φ) este:
![]() . (27)
. (27)
Daca se utilizeaza notiunea de permanenta magnetica definita prin relatia:
![]() , (28)
, (28)
in care Fm este forta magnetomotoare a circuitului, atunci inductivitatea poate fi exprimata prin relatia:
![]() , (29)
, (29)
adica inductivitatea este dependenta de permeanta magnetica a circuitului. In cazul in care circuitele magnetice poseda intrefier, relatia (29) trebuie scrisa sub forma:
![]() (30)
(30)
in care ![]() este coeficientul
conductibilitatii magnetice pentru fluxurile produse de Fm.
este coeficientul
conductibilitatii magnetice pentru fluxurile produse de Fm.
Campul rezultant din masina se imparte in mod obisnuit, in doua componente: campul inductiei mutuale - adica campul magnetic care inlantuie toate spirele infasurarilor care se gasesc intr-un cuplaj magnetic si campul de dispersie - adica campul care se inlantuie cu spirele unei singure infasurari desi ea se afla cuplata magnetic si cu alte infasurari.
La proiectarea masinilor electrice se urmareste ca fluxul de dispersie sa fie cat mai mic (doar cateva procente din fluxul inductiei mutuale). In final trebuie adaugat ca, desi procesele conversiei de energie sunt conditionate de fluxul magnetic rezultant din masina, totusi cea mai mare importanta o are campul inductiei mutuale denumit si campul principal al masinii.
B. Campul principal
Relatia dintre inductia magnetica B si curentii electrici care produc campul magnetic se stabileste cu ajutorul teoremei lui Ampère:
![]() , (31)
, (31)
in care Hl Bl
reprezinta proiectiile vectorilor ![]() pe vectorul deplasarii elementare
pe vectorul deplasarii elementare![]() . De fapt integrala de contur
din (31) se calculeaza pe anumite portiuni (convenabil alese)
ale conturului (Γ) respectiv se iau in considerare integralele de
tipul,
. De fapt integrala de contur
din (31) se calculeaza pe anumite portiuni (convenabil alese)
ale conturului (Γ) respectiv se iau in considerare integralele de
tipul, ![]() care se numesc forte magnetomotoare (f.m.m.) a
prtiunilor respective de contur (Γ).
care se numesc forte magnetomotoare (f.m.m.) a
prtiunilor respective de contur (Γ).
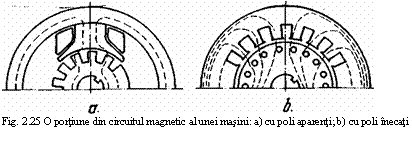 De obicei calculul circuitului magnetic
al unei masini electrice se face in regim de mers in gol cand
curentul indusului este nul sau aproape nul. O portiune din
circuitul magnetic al unei masini cu poli aparenti si cu poli
inecati este data in figura 25.
De obicei calculul circuitului magnetic
al unei masini electrice se face in regim de mers in gol cand
curentul indusului este nul sau aproape nul. O portiune din
circuitul magnetic al unei masini cu poli aparenti si cu poli
inecati este data in figura 25.
Circuitul magnetic al unei masini cu poli aparenti sau inecati se imparte pe cinci portiuni principale astfel incat (f.m.m) totala se noteaza sub forma:
![]() , (32)
, (32)
in care
avem: ![]() este f.m.m. pentru
intrefierul masinii;
este f.m.m. pentru
intrefierul masinii; ![]() este f.m.m pentru
dintii rotorici si/sau statorici;
este f.m.m pentru
dintii rotorici si/sau statorici; ![]() este f.m.m. pentru
poli;
este f.m.m. pentru
poli; ![]() este f.m.m.
corespunzatoare armaturii rotorice;
este f.m.m.
corespunzatoare armaturii rotorice; ![]() este f.m.m.
pentru armatura statorica. Unele amanunte specifice pentru
anumite tipuri de masini se vor prezenta la capitolele respective.
este f.m.m.
pentru armatura statorica. Unele amanunte specifice pentru
anumite tipuri de masini se vor prezenta la capitolele respective.
F.m.m. pentru intrefier ![]() se determina cu
relatia:
se determina cu
relatia:
![]()
![]() , (33)
, (33)
in care ![]() este intensitatea
campului magnetic din intrefierul masinii; δ este marimea
intrefierului, iar kδ este coeficientul intrefierului,
care tine seama ca linia campului magnetic din intrefier se
lungeste datorita existentei crestaturilor retorice
si/sau statorice: kδ=1,1,.,1,5.
este intensitatea
campului magnetic din intrefierul masinii; δ este marimea
intrefierului, iar kδ este coeficientul intrefierului,
care tine seama ca linia campului magnetic din intrefier se
lungeste datorita existentei crestaturilor retorice
si/sau statorice: kδ=1,1,.,1,5.
F.m.m. pentru dinti se calculeaza cu relatia:
![]() , (34)
, (34)
in cure Hz este intensitatea medie a campului magnetic in dinte, iar lz este inaltimea dintelui. Daca inductia magnetica din dinte este constanta in diversele sale sectiuni, atunci Hz se considera unica pentru toata lungimea dintelui, dar daca inductia B este variabila, atunci hz mediu se obtine prin determinarea intensitatilor campului in trei sectiuni ale dintelui.
F.m.m. pentru pol se calculeaza cu relatia:
![]() , (35)
, (35)
in care Hp este intensitatea campului magnetic din pol, iar lp este lungimea polului.
F.m.m. pentru jugul rotorului se calculeaza cu relatia:
![]() , (36)
, (36)
in care Hγ este intensitatea campului magnetic corespunzatoare jugului rotoric, iar lγ este lungimea corespunzatoare.
F.m.m. pentru jugul statorului se calculeaza cu relatia:
![]() , (37)
, (37)
in care Hs este intensitatea campului magnetic corespunzatoare jugului statoric, iar ls este lungimea acestui jug.
La masini cu poli inecati, f.m.m. pentru jugul rotoric si statoric se calculeaza luand in considerare coeficientul influentei faptului ca inductia magnetica nu se distribuie uniform in sectiunile jugurilor respective.
In mod obisnuit, la calculul circuitului magnetic al masinii se stabileste inductia din intrefierul masinii Bδ , se calculeaza fluxul inductiei magnetice conform cu suprafata din intrefier corespunzatoare unui pol magnetic, iar dupa aceea se determina inductia magnetica pe diverse portiuni ale circuitului magnetic luand in considerare geometria (sectiuni, lungimi etc) portiunii respective. Apoi in functie de calitatea otelului din care este realizata portiunea de circuit magnetic, din tabele sau curbe specializate se determina intensitatile corespunzatoare ale campului magnetic.
Prin sumare f.m.m. avem:
![]() (38)
(38)
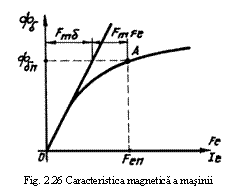 in care Fe este f.m.m. a
infasurarii de excitatie. Secventele de calcul
mentionate anterior se repeta pentru mai multe valori ale lui Bδ,
iar dupa aceea se traseaza caracteristica de magnetizare a
masinii sau caracteristica magnetica a masinii.
Φδ= f(F) - figura 26. Portiunea de inceput a
caracteristicii corespunde starii de nesaturatie magnetica a
circuitului magnetic al masinii si ea se determina cu
functia Φδ= f
(Fmδ) pentru
ca f.m.m. corespunzatoare portiunilor din fier ale circuitului
magnetic al masinii sunt neglijabile.
in care Fe este f.m.m. a
infasurarii de excitatie. Secventele de calcul
mentionate anterior se repeta pentru mai multe valori ale lui Bδ,
iar dupa aceea se traseaza caracteristica de magnetizare a
masinii sau caracteristica magnetica a masinii.
Φδ= f(F) - figura 26. Portiunea de inceput a
caracteristicii corespunde starii de nesaturatie magnetica a
circuitului magnetic al masinii si ea se determina cu
functia Φδ= f
(Fmδ) pentru
ca f.m.m. corespunzatoare portiunilor din fier ale circuitului
magnetic al masinii sunt neglijabile.
Punctul nominal de lucru A, corespunzator lui Fen, se alege in cotul curbei.
De
obicei ![]() se determina pentru o pereche de poli (un N si un
S), de aceea intr-un contur (Γ) complet, sunt cuprinse doua
spatii de intrfier, doi dinti rotorici si/sau statorici
doua lungimi de pol, o lungime
corespunzatoare (unei perechi de poli) din jug rotoric si statoric.
Dupa determinarea lui Fe
din (38) se pot calcula amper-spirele corespunzatoare unui pol de
excitatie
se determina pentru o pereche de poli (un N si un
S), de aceea intr-un contur (Γ) complet, sunt cuprinse doua
spatii de intrfier, doi dinti rotorici si/sau statorici
doua lungimi de pol, o lungime
corespunzatoare (unei perechi de poli) din jug rotoric si statoric.
Dupa determinarea lui Fe
din (38) se pot calcula amper-spirele corespunzatoare unui pol de
excitatie
![]()
Este cunoscut deja ca la masini heteropolare imaginea campului magnetic se repeta pentru fiecare pereche de poli, de aceea calculul circuitului magnetic se realizeaza pentru o singura pereche de poli. F.m.m. totala poate fi descompusa in doua componente:
![]()
in care FmFe este f.m.m. corespunzatoare portiunilor din fier ale circuitului magnetic. Raportul
![]()
se
numeste coeficientul de saturatie al masinii, care
depinde de intrefierul masinii si de gradul de saturatie al portiunilor din fier al
circuitului magnetic al masinii - ![]() . La masini sincrone si cele de c.c. ks
= 1,1,,l,3, iar la cele sincrone ks = 1,2,.,1,6.
. La masini sincrone si cele de c.c. ks
= 1,1,,l,3, iar la cele sincrone ks = 1,2,.,1,6.
Din experienta de proiectare a masinilor electrice rezulta ca inductiile magnetice din intrefier si dinti determina in final caracteristicile energetice si de gabarit ale masinii.
O inductie cu distributie sinusoidala in intrefierul unei masini nesaturate cu poli inecati se poate obtine numai printr-o distributie sinusoidala a infasurarilor. La masini nesaturate cu poli aparenti forma curbei inductiei magnetice din intrefier se determina cu profilul intrefierului din dreptul polului: pentru o distributie a inductiei in intrefier apropiata de cea sinusoidala, intrefierul se profileaza cu relatia (fig. 27).
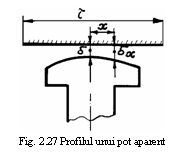
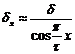 , (42)
, (42)
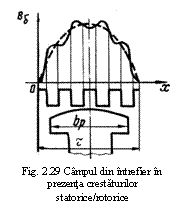
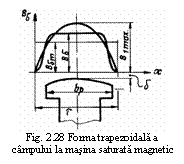 in care δ este marimea intrefierului in axa polului. In general, la
capetele polului intrefierul este circa (1,5,,l,6)xδ. Desi la masini cu poli
aparenti intrefierul se realizeaza dupa relatia (42), totusi curba de variatia a
inductie magnetice are o forma 'trapezoidala'- figura 28
(pentru ca masina prezinta saturatie magnetica) - iar
armonicile superioare au amplitudinile relativ mici. In figura 28 este
mentionata amplitudinea fundamentalei inductiei B1max (rezultata din descompunerea in
seria Fourier a curbei trapezoidale), valoarea medie a inductiei din
intrefier Bδm (utilizata in mod obisnuit in
calcule), latimea polului bp si a pasului polar
τ.
in care δ este marimea intrefierului in axa polului. In general, la
capetele polului intrefierul este circa (1,5,,l,6)xδ. Desi la masini cu poli
aparenti intrefierul se realizeaza dupa relatia (42), totusi curba de variatia a
inductie magnetice are o forma 'trapezoidala'- figura 28
(pentru ca masina prezinta saturatie magnetica) - iar
armonicile superioare au amplitudinile relativ mici. In figura 28 este
mentionata amplitudinea fundamentalei inductiei B1max (rezultata din descompunerea in
seria Fourier a curbei trapezoidale), valoarea medie a inductiei din
intrefier Bδm (utilizata in mod obisnuit in
calcule), latimea polului bp si a pasului polar
τ.
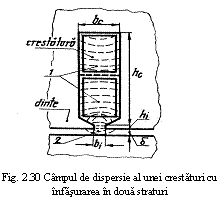 Existenta crestaturilor
statorice modifica reluctanta magnetica a intrefierului in
dreptul acestor crestaturi si in acest fel modifica de fapt
campul magnetic din intrefier - el apare aproximativ ca in figura 29.
Existenta crestaturilor in stator si in rotor complica mai
mult imaginea campului magnetic din intrefierul masinii, dar armonica
fundamentala totusi se modifica putin. Toate acestea se
refera la cazul functionarii in gol a masinii. Cand
masina se gaseste in sarcina, campul magnetic din intrefierul
masinii este conditionat atat de curentii din stator cat si
de cei din rotor, ceea ce duce la deformarea curbei campului, respectiv la o
micsorare a acestuia in raport cu cazul functionarii in gol.
Influenta curentului de sarcina asupra caracteristicilor masinii
este denumita reactia indusului.Desigur ca reactia
indusului la diverse tipuri de masini este diferita si ea va fi
prezentata mai amanuntit la capitolele respective.
Existenta crestaturilor
statorice modifica reluctanta magnetica a intrefierului in
dreptul acestor crestaturi si in acest fel modifica de fapt
campul magnetic din intrefier - el apare aproximativ ca in figura 29.
Existenta crestaturilor in stator si in rotor complica mai
mult imaginea campului magnetic din intrefierul masinii, dar armonica
fundamentala totusi se modifica putin. Toate acestea se
refera la cazul functionarii in gol a masinii. Cand
masina se gaseste in sarcina, campul magnetic din intrefierul
masinii este conditionat atat de curentii din stator cat si
de cei din rotor, ceea ce duce la deformarea curbei campului, respectiv la o
micsorare a acestuia in raport cu cazul functionarii in gol.
Influenta curentului de sarcina asupra caracteristicilor masinii
este denumita reactia indusului.Desigur ca reactia
indusului la diverse tipuri de masini este diferita si ea va fi
prezentata mai amanuntit la capitolele respective.
C. Campul de scapari
Referindu-ne la campul de dispersie dintr-o masina electrica acesta poate fi impartit in trei parti: campul de dispersie al crestaturilor; campul de dispersie al partilor frontale ale infasurarilor si campul de dispersie diferential. Campul de dispersie al crestaturilor se poate imparti la randul sau in campul de dispersie din crestatura l si campul de dispersie din capetele dintilor 2 - figura 30. Campul de dispersie din crestatura depinde de geometria acesteia: latimea bc, inaltimea hc, inaltimea istmului (slitului) crestaturii hi, latimea istmului bi. Campul de dispersie din crestatura isi complica configuratia cand elementele conducatoare de curent, montate in crestatura sunt parcurse de curent si determinarea analitica a campului de dispersie din crestatura este posibila numai pentru, crestaturi cu geometrie simpla, iar in celelalte cazuri se utilizeaza unele formule empirice.
Campul de dispersie al capetelor frontale ale infasurarilor depinde de forma (geometria) capetelor frontale, de numarul polilor si de insusi tipul infasurarii masinii. De obicei campul de dispersie al capetelor frontale este mai mic decat cel din crestatura.
Desigur ca in intrefierul masinii in afara de armonica fundamentala a campului magnetic exista si armonici superiore. In calculul masinii electrice se ia in considerare numai armonica fundamentala a campului, iar armonicile superioare ale campului formeaza campul de dispersie diferential.
7. INFASURARILE MASINILOR ELECTRICE
Infasurarile masinilor electrice reprezinta niste conture inchise prin care circula curenti si cu ajutorul carora se realizeaza campul magnetic al masinilor. Din punct de vedere constructiv infasurarile masinilor sunt foarte diversificate plecand de la forma de cilindri masivi realizati din material feromagnetic si nemagnetic pana la complexele infasurarii multifazate ale masinilor de c.a. si c.c.
Infasurarea unei masini este o componenta constructiva de baza a acesteia si de ea depind parametri energetici si de gabarit ai masinii. Infasurarile unei masini se executa sub forma monofazata, bifazata, trifazata si multifazata, dar ca regula generala infasurarile unei masini sunt simetrice. Pentru o masina trifazata de exemplu, simetria infasurarii se refera la:
- toate cele trei infasurari se gasesc sub influenta aceluiasi camp magnetic;
- in toate cele trei infasurari se induc aceleasi valori efective ale t.e.m.;
- f.m.m. ale celor trei infasurari trebuie sa fie defazate cu 1200.
In afara de acestea, infasurarile masinilor trebuie sa posede o siguranta mecanica si electrica in functionare (sa suporte anumite eforturi mecanice, sa reziste la anumite tensiuni etc), sa fie termostabile (pana la anumite nivele de temperatura), sa fie executabile tehnologic si sa fie posibila o reparare a acestora.
Din punctul de vedere al inlantuirii cu campurile magnetice infasurarile masinilor se pot imparti in doua grupe mari: infasurari concentrate si infasurari distribuite.
La infasurari concentrate, practic toate spirele infasurarii se inlantuie, la un moment dat, cu acelasi camp magnetic. In cadrul acestui tip pot fi incluse infasurarile transformatoarelor electrice si infasurarile de excitatie montate pe poli aparenti ai masinilor sincrone si celei de c.c.
In cadrul tipului de infasurari distribuite se includ infasurarile statorice ale masinilor asincrone si sincrone, infasurarile rotorice ale masinilor de c.c. si ale unor masini asincrone, unele infasurari de compensatie si speciale.
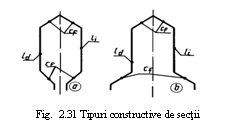 Infasurarile concentrate
(sau de tip bobina) se executa din conductoare circulare sau dreptunghiulare,
acestea din urma montate fie pe lat, fie pe muchie (cant ).
Infasurarile concentrate
(sau de tip bobina) se executa din conductoare circulare sau dreptunghiulare,
acestea din urma montate fie pe lat, fie pe muchie (cant ).
La executia infasurarilor distribuite este necesar sa fie precizata dispunerea tuturor elementelor constructive ale acestora in campul magnetic al masinii si cum se face legarea diverselor elemente constructive.
De obicei schema unei infasurari se reprezinta intr-un plan si reprezinta desfasurata, in planul respectiv, a suprafetei cilindrice a rotorului sau statorului masinii in crestaturile careia este montata infasurarea reala; ea se mai numeste schema desfasurata a infasurarii. Distantele geometrice in cadrul acestei scheme nu au nici o semnificatie fizica, dar pozitiile relative a diverselor elemente isi au importanta lor
Infasurarile distribuite se pot imparti la randul lor in infasurari simple si infasurari compuse formate de obicei din doua sau chiar trei infasurari simple, infasurarile simple se pot executa intr-un singur strat sau in dublu strat. Elementul constructiv de baza al unei infasurari este sectia care de obicei contine mai multe spire si la care se disting latura de ducere (ld), latura de intoarcere (li) si capetele frontale (cf) ale sectiei. In figura 31 sunt reprezentate doua tipuri de sectii formate dintr-o singura spira.
 La infasurarile realizate in dublu strat latura de ducere a
unei sectii se monteaza in partea inferioara (de fund) a unei
crestaturi, iar latura de intoarcere a aceleiasi sectii se
monteaza la partea superioara (spre istm) a altei
crestaturii, iar pentru a realiza acest sistem de montare - figura 32 -
capetele frontale ale sectiei se profileaza
intr-un mod special . Cele doua
laturi ale sectiei se vor gasi in planuri diferite, pentru ca
vor trebui sa tina seama si de curbura suprafetei
cilindrice ale statorului sau rotorului in care urmeaza sa se
incadreze.
La infasurarile realizate in dublu strat latura de ducere a
unei sectii se monteaza in partea inferioara (de fund) a unei
crestaturi, iar latura de intoarcere a aceleiasi sectii se
monteaza la partea superioara (spre istm) a altei
crestaturii, iar pentru a realiza acest sistem de montare - figura 32 -
capetele frontale ale sectiei se profileaza
intr-un mod special . Cele doua
laturi ale sectiei se vor gasi in planuri diferite, pentru ca
vor trebui sa tina seama si de curbura suprafetei
cilindrice ale statorului sau rotorului in care urmeaza sa se
incadreze.
7.1.INFASURARI INTR-UN STRAT
Infasurarile executate intr-un singur strat in functie de dispunerea capetelor frontale, se impart in infasurari concentrice, caz in care capetele frontale ale sectiilor se cuprind unele pe altele, respectiv bi sau trietajate, caz in care capetele frontale se dispun in doua, respectiv trei plane diferite - figura 33 a si b.
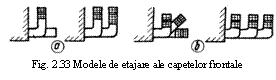 La o infasurare a unei
masini electrice, in general, se iau in considerare parametri
urmatori: m - numarul de faze (cazul masinilor de c.a.); z - numarul total de crestaturi dispuse pe statorul sau
rotorul masinii; q - numarul de crestaturi pe pol si
faza (cazul masinilor de c.a.). Sa luam exemplul
unei infasurari intr-un
strat, in doua etaje, cu datele: z = 24; 2p = 4; m = 3.
La o infasurare a unei
masini electrice, in general, se iau in considerare parametri
urmatori: m - numarul de faze (cazul masinilor de c.a.); z - numarul total de crestaturi dispuse pe statorul sau
rotorul masinii; q - numarul de crestaturi pe pol si
faza (cazul masinilor de c.a.). Sa luam exemplul
unei infasurari intr-un
strat, in doua etaje, cu datele: z = 24; 2p = 4; m = 3.
Pentru a realiza schema desfasurata a unei infasurari se realizeaza unele calcule:
a)- numarul de crestaturi pe pol si faza;
![]() , (43)
, (43)
b)- unghiul geometric si cel electric dintre doua crestaturi;
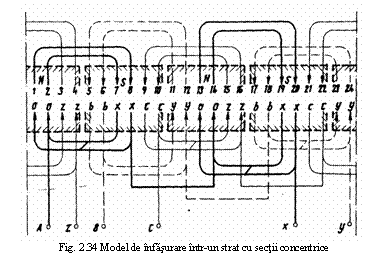
![]() ,
,
respectiv
![]() , (44)
, (44)
c)- pasul polar.
![]() crestaturi(45)
crestaturi(45)
La o infasurare se mai defineste asa-numitul pas principal al infasurarii cu relatia:
![]() , (45a)
, (45a)
in care ε este un numar, in general, fractionar care se scade sau se aduna la primul termen astfel incat y1 sa fie totdeauna un numar intreg. In principiu, de exemplu, daca ε = 6,4, atunci y1 (care nu poate fi decat un numar intreg) nu poate fi decat egal cu 6 (ε = -0,4) sau egal cu 7 (ε = +0,6), avand in vedere faptul ca pasul principal reprezinta distanta, luata in numar de crestaturi, dintre latura de ducere a unei sectii si latura de intoarcere a aceleiasi sectii.
Daca y1 = τ, se spune ca infasurarea are pas diametral; daca y1 > τ, se spune ca infasurarea are pas lungit; daca y1 < τ - avem pas scurtat, acesta fiind cel mai utilizat in practica din motive de economie de material (cupru).
Sa admitem in cadrul exemplului nostru y1 = τ si atunci schema desfasurata a infasurarii apare ca in figura 34.
In aceasta schema sunt mentionate inceputurile si sfarsiturile de faza (A-X), (B-Y), (C-Z), cu precizarea ca intre doua inceputuri de faza, de exemplu intre A si B, trebuie sa fie 1200 electrice ceea ce se verifica pentru ca inceputul de faza A este montat in crestatura 2, iar inceputul de faza B in crestatura 6 - adica ΔzAB = 6-2 = 4 crestaturi, respectiv ΔzABαe = 4*300=1200.
In
schema precedenta sunt evidentiati polii magnetici ce apar la un
moment dat (la schimbarea sensului curentului, polaritatea lor se
inverseaza), dar mai trebuie mentionat ca sectiile
infasurarii nu respecta de fapt valoarea pasului diametral
y1 = τ = 6 crestaturi. Intr-adevar, se admite
urmatoarea regula pentru notarea sectiilor: latura de ducere
a sectiei se va nota cu numarul corespunzator crestaturii
in care este amplasata, de asemenea
si latura de intoarcere a sectiei dar numarul va fi apostrofat, iar
ambele numere despartite printr-o liniuta vor fi cuprinse intre
paranteze rotunde. In aceasta idee prima sectie (2-7') a fazei
(A-X) are pasul principal y1=5cr.,
iar a doua sectie (1-8') a aceleiasi faze are y1=7cr. -
adica sectiile nu au aceeasi 'deschidere' ceea ce
complica tehnologia de executie a sectiunii (dar in medie ![]() ).
).
O alta varianta a infasurarilor intr-un strat sunt asa-numitele infasurari in lant, care permit o asezare mai simpla a capetelor frontale, iar toate sectiile infasurarii au aceeasi geometrie.
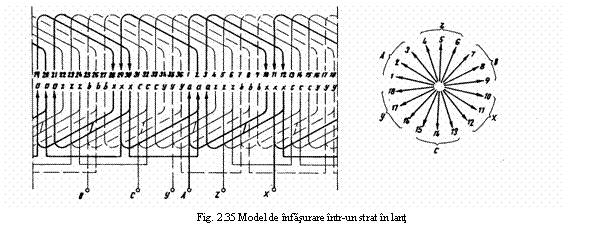 Un exemplu de astfel de infasurare
cu parametri z = 36 crestaturi, 2p = 4, m = 3 este dat in figura 35.
Un exemplu de astfel de infasurare
cu parametri z = 36 crestaturi, 2p = 4, m = 3 este dat in figura 35.

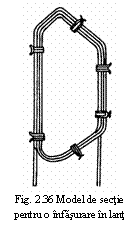 Forma de executie a bobinelor este
aproximativ aceeasi cu cea din schema si ea este precizata
in figura 36, iar capetele frontale ale unei infasurari
lant sunt aratate in figura 37. Din figura 36 se observa ca
o sectie are o latura lunga si o latura scurta.
Pasul infasurarii in lant trebuie sa fie totdeauna un numar
impar astfel incat daca laturile lungi ale sectiilor
ocupa crestaturi cu numar impar, laturile scurte vor ocupa
crestaturi cu un numar par. In cadru exemplului precedent de
infasurare in lant avem τ = 9cr, q = 3cr si se
admite y1 (pas diametral).
Forma de executie a bobinelor este
aproximativ aceeasi cu cea din schema si ea este precizata
in figura 36, iar capetele frontale ale unei infasurari
lant sunt aratate in figura 37. Din figura 36 se observa ca
o sectie are o latura lunga si o latura scurta.
Pasul infasurarii in lant trebuie sa fie totdeauna un numar
impar astfel incat daca laturile lungi ale sectiilor
ocupa crestaturi cu numar impar, laturile scurte vor ocupa
crestaturi cu un numar par. In cadru exemplului precedent de
infasurare in lant avem τ = 9cr, q = 3cr si se
admite y1 (pas diametral).
INFASURARI IN DOUA STRATURI
Pentru a intelege mai bine principiul de formare a unei infasurari in doua straturi, se ia in considerare o infasurare inelara a unei masini de c.c. de tip vechi (cu circuitul magnetic in inel - masina tip Gramme), reprezentata in figura 38a si o infasurare trifazata a unei masini sincrone inversate reprezentate in figura 38b; infasurarea inelara este montata pe un miez toroidal si este o infasurare inchisa (nu are un inceput, respectiv un sfarsit). Daca se monteaza o pereche de perii pe o axa (axa periilor sau axa neutra) perpendiculara pe axa polilor si le facem sa alunece pe un element constructiv al masinii de c.c. denumit colector (la care se racordeaza infasurarea inelara), atunci prin aceste perii se poate culege c.c.
Pentru a obtine o tensiune alternativa trifazata, este necesar ca de la infasurarea inelara sa fie luate trei prize de tensiune, dispuse la 1200, si racordate la trei inele colectoare pe care aluneca periile respective-figura 38 b. De fapt in figura mentionata infasurarea inelara este formata din 12 sectii (fiecare sectie formata dintr-o singura spira), dar in principiu cu aceasta infasurare se poate obtine o tensiune alternativa 12-fazata, daca de la flecare sectie a infasurarii se ia o 'priza de tensiune' si se racordeaza la un inel colector. In acest fel numarul fazelor depinde de executia infasurarii, de numarul 'prizelor de tensiune' realizate, respectiv notiunea de faza a tensiunii si numarul de faze a infasurarii este legat in final de unghiul electric dintre fazorii tensiunilor de faza sau de unghiul geometric (spatial) dintre fazele infasurarii la masina bipolara. Deci de la una si aceeasi infasurare se poate obtine o tensiune trifazata, sau multifazica sau de c.c. in cazul existentei colectorului.
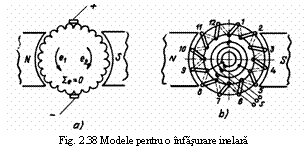 La infasurarea inelara -
figura 38a - se poate observa usor existenta a doua ramuri
paralele simetrice in raport cu periile (+ , -); ele se numesc cai de
curent pentru ca prin aceste ramuri paralele circula curentul de
sarcina de la peria (+) la peria (-).
La infasurarea inelara -
figura 38a - se poate observa usor existenta a doua ramuri
paralele simetrice in raport cu periile (+ , -); ele se numesc cai de
curent pentru ca prin aceste ramuri paralele circula curentul de
sarcina de la peria (+) la peria (-).
Pe de alta parte, intr-o infasurare inelara t.e.m. se induce numai in laturile sectiilor care sunt dispuse pe "suprafata exterioara a miezului toroidal" pentru ca numai acele portiuni ale infasurarii 'taie' liniile campului magnetic. De aceea pentru a mari eficienta materialului utilizat pentru infasurari, este necesar sa se mareasca portiunea activa a infasurarilor, respectiv portiunea care 'taie' liniile campului magnetic. Aceasta se poate obtine prin montarea pe suprafata exterioara a miezului toroidal si a laturilor sectiilor care in mod obisnuit la o infasurare inelara apar montate pe suprafata interioara a miezului toroidal. Astfel se ajunge la infasurari tip toba la care ambele laturi ale unei sectii apar montate la exteriorul rotorului - figura 39b.
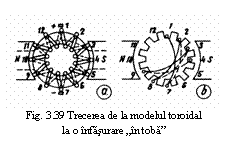 Infasurarile tip toba
sunt deja infasurari executate in doua straturi, caz
in care o latura a sectiei este dispusa la partea
inferioara a crestaturii, iar cealalta latura la partea
superioara a unei alte crestaturi. Principial o
infasurare inelara si una tip toba nu
difera, diferenta este
legata numai de tehnologia executiei.
Infasurarile tip toba
sunt deja infasurari executate in doua straturi, caz
in care o latura a sectiei este dispusa la partea
inferioara a crestaturii, iar cealalta latura la partea
superioara a unei alte crestaturi. Principial o
infasurare inelara si una tip toba nu
difera, diferenta este
legata numai de tehnologia executiei.
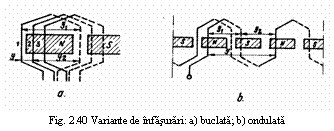 Asa cum rezulta deci din cele
mentionate anterior si din figura 38a si b infasurarile
pentru c.a. si c.c. nu se deosebesc principial una de alta si pot fi transformate una in alta (in
anumite conditii) in functie de existenta colectorului sau a inelelor colectoare.
Asa cum rezulta deci din cele
mentionate anterior si din figura 38a si b infasurarile
pentru c.a. si c.c. nu se deosebesc principial una de alta si pot fi transformate una in alta (in
anumite conditii) in functie de existenta colectorului sau a inelelor colectoare.
In alta ordine de idei, trebuie precizat faptul ca in practica cel mai adesea se foloseste infasurarea in dublu strat pentru ca ea permite alegerea mai usoara a unui pas adecvat care conduce la o economie de cupru, de material izolant si permite o mai buna mecanizare a executiei sectiilor.
Infasurarile in dublu strat se impart in doua grupe: infasurari buclate (tipul sectiei buclate - figura 31 a) si infasurari ondulate (tipul sectiei ondulate - figura 31 b). In cadrul acestor tipuri de infasurari, in afara de pasul principal y1, se mai definesc urmatoarele tipuri de pasi:
pasul de intoarcere (pasul secundar) - y2 - ca fiind distanta luata in numar de crestaturi intre latura de intoarcere a unei sectii si latura de ducere a sectiei urmatoare;
pasul rezultant - y - ca fiind distanta luata in numar de crestaturi intre latura de ducere a unei sectii si latura de ducere a sectiei urmatoare. In figura 40a si b se mentioneaza pasii respectivi pentru tipul buclat, respectiv ondulat de infasurare.
In general intr-o schema a unei infasurari latura sectiei care este 'asezata' la partea superioara a crestaturii se figureaza cu linia plina, iar latura sectiei asezata la partea inferioara a crestaturii se figureaza cu linia punctata, ceea ce inseamna ca pentru fiecare crestatura din schema vor fi trasate doua linii (paralele si apropiate) una plina si una punctata avand in vedere ca este vorba de o infasurare in dublu strat. De asemenea, din schemele figurii 40 rezulta ca pentru o infasurare buclata exista relatia:
![]() (46)
(46)
iar pentru o infasurare ondulata avem:
![]() (47)
(47)
Desigur si in acest caz putem avea infasurari cu pas scurtat, pas diametral sau pas lungit, cel mai des intalnit in practica fiind pasul scurtat.
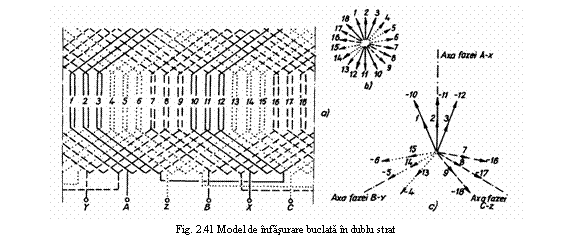 In
figura 41 este dat un exemplu de
infasurare buclata cu parametri: z = 18 cr; m = 3; 2p = 2 din
care rezulta apoi q = 18/(3) = 3
cr; τ = 18/2 = 9 cr; pasul
este diametral deci y1 = τ = 9cr; y2 = 8cr,
respectiv y = l cr.
In
figura 41 este dat un exemplu de
infasurare buclata cu parametri: z = 18 cr; m = 3; 2p = 2 din
care rezulta apoi q = 18/(3) = 3
cr; τ = 18/2 = 9 cr; pasul
este diametral deci y1 = τ = 9cr; y2 = 8cr,
respectiv y = l cr.
In figura 42a este redata schema desfasurata a unei infasurari buclate cu z = 24 cr, 2p = 4, m = 3 si pas scurtat y1 = 8, iar in figura 42b se prezinta schema cu parametri z = 24 cr. 2p = 4, m = 3 si q = 2 a unei infasurari ondulate.
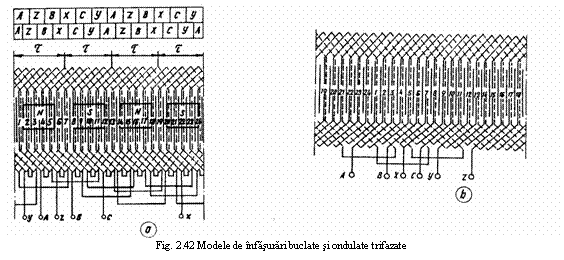 In figura 43 este redata schema desfasurata pentru
o infasurare buclata de c.c. cu parametri z = 12 cr, 2p = 2, k
=12 lamele de
colector.
In figura 43 este redata schema desfasurata pentru
o infasurare buclata de c.c. cu parametri z = 12 cr, 2p = 2, k
=12 lamele de
colector.
In principiu infasurarea rotorica pentru o masina de c.c. nu se deosebeste de o infasurare in dublu strat de c.a. Dar existenta unui convertor mecanic de frecventa, care este colectorul masinii de c.c., conduce la unele deosebiri in tehnologia de executie.
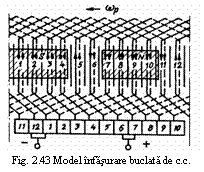 Pentru a imbunatati comutatia masinii de c.c.
se cauta micsorarea numarului de spire dintr-o sectie a
infasurarii retorice si respectiv marirea numarului
de lamele ale colectorului. Infasurarile rotorice ale
masinii de c.c. pot fi, de asemenea, de tip buclat sau ondulat, iar infasurarile
compuse se fac din doua sau trei infasurari simple de tip
buclat sau ondulat. La infasurarile simple de tip buclat a
masinii de c.c. avem totdeauna 2a = 2p, iar la cele de tip ondulat 2a = 2,
in care cu a s-a notat numarul perechilor de cai de curent.
Existenta cailor paralele - adica a cailor de curent - se
observa cu usurinta in cazul unei masini Gramme cu 4
poli reprezentata in figura 44. Masina are 4 perii (2p = nr.
periilor), respectiv 4 cai de curent care apar legate in paralel intre
ele.
Pentru a imbunatati comutatia masinii de c.c.
se cauta micsorarea numarului de spire dintr-o sectie a
infasurarii retorice si respectiv marirea numarului
de lamele ale colectorului. Infasurarile rotorice ale
masinii de c.c. pot fi, de asemenea, de tip buclat sau ondulat, iar infasurarile
compuse se fac din doua sau trei infasurari simple de tip
buclat sau ondulat. La infasurarile simple de tip buclat a
masinii de c.c. avem totdeauna 2a = 2p, iar la cele de tip ondulat 2a = 2,
in care cu a s-a notat numarul perechilor de cai de curent.
Existenta cailor paralele - adica a cailor de curent - se
observa cu usurinta in cazul unei masini Gramme cu 4
poli reprezentata in figura 44. Masina are 4 perii (2p = nr.
periilor), respectiv 4 cai de curent care apar legate in paralel intre
ele.
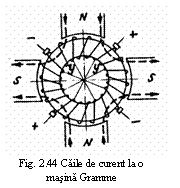 La masini
de c.c. mai apare insa un aspect specific: datorita
neuniformitatii intrefierului (prin existenta polilor
aparenti), t.e.m. induse in caile de curent pot fi diferite si
cum caile de curent sunt legate in paralel intre ele, aceasta va conduce
la producerea unor curenti egalizatori care vor circula prin
infasurarea rotorica si prin periile de aceeasi
polaritate inrautatind polaritatea masinii. Pentru a
elimina aceste efecte, respectiv pentru "a descarca" periile de
curenti egalizatori, se executa la infasurare legaturi
de egalizare Y (fig. 44) care unesc toate punctele echipotentiale ale
infasurarii rotorice. Infasurarile de tip ondulat
nu necesita legaturi de egalizare deoarece insasi capetele
sectiilor ondulate unesc punctele echipotentiale ale infasurarii
La masini
de c.c. mai apare insa un aspect specific: datorita
neuniformitatii intrefierului (prin existenta polilor
aparenti), t.e.m. induse in caile de curent pot fi diferite si
cum caile de curent sunt legate in paralel intre ele, aceasta va conduce
la producerea unor curenti egalizatori care vor circula prin
infasurarea rotorica si prin periile de aceeasi
polaritate inrautatind polaritatea masinii. Pentru a
elimina aceste efecte, respectiv pentru "a descarca" periile de
curenti egalizatori, se executa la infasurare legaturi
de egalizare Y (fig. 44) care unesc toate punctele echipotentiale ale
infasurarii rotorice. Infasurarile de tip ondulat
nu necesita legaturi de egalizare deoarece insasi capetele
sectiilor ondulate unesc punctele echipotentiale ale infasurarii
Alte aspecte specifice infasurarilor de c.a. si de c.c. vor fi prezentate si in cadrul capitolelor respective.
8. T.E.M. INDUSE IN INFASURARILE MASINILOR ELECTRICE
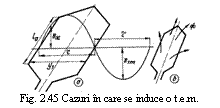
A. Generalitati privind t.e.m. induse
In capitolul 1 s-a aratat ca, in cazul general, intr-un contur inchis (Γ) pot fi induse doua tipuri de t.e.m. induse: t.e.m. de miscare, respectiv t.e.m. de transformare; ele pot exista simultan sau fiecare tip in parte. O t.e.m. se induce intr-o spira (contur inchis) daca:
a) spira se deplaseaza in raport cu un camp magnetic fix si constant in timp - figura 45a;
b)campul magnetic, constant in timp, se deplaseaza in raport cu spira fixa - figura 45a ;
c) spira este fixa dar se inlantuie cu un camp magnetic variabil in timp - figura 45b.
Deci, in general, se induce o t.e.m. intr-o spira, atunci cand exista o deplasare spatiala a campului magnetic si a spirei in raport unul cu altul si la variatia in timp a fluxului magnetic ce se inlantuie cu spira.
T.e.m. de miscare poate fi determinata, in general, cu relatia (1.34), adica relatia lui Faraday :
![]() ,
,
ceea ce in marimi obisnuite se poate nota sub forma:
![]()
![]() (48)
(48)
in care la este lungimea activa (adica cea care "taie" liniile campului magnetic de inductie Bx), iar v este viteza liniara de deplasare a spirei.
Daca se considera o sectie a unei infasurari formata din ws spire, atunci t.e.m. indusa in sectie este:
![]() , (49)
, (49)
in care trebuie luat in
evidenta fluxul magnetic total care se inlantuie cu
sectia considerata ![]() si in care
si in care ![]() este fluxul magnetic fascicular al sectiei,
adica fluxul magnetic corespunzator unei singure spire a
sectiei. Daca fluxul magnetic are o variatie armonica in
timp
este fluxul magnetic fascicular al sectiei,
adica fluxul magnetic corespunzator unei singure spire a
sectiei. Daca fluxul magnetic are o variatie armonica in
timp
![]() ,
,
atunci
![]() ,
,
respectiv
![]()
![]() , (50)
, (50)
adica t.e.m. indusa este totdeauna defazata in urma fluxului (care o induce) cu π/2 si are ca si fluxul magnetic o variatie armonica.
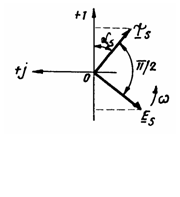 Cei doi parametri avand
variatii armonice, lor li se pot asocia fazori corespunzatori, iar in
figura 46 sunt reprezentati fazorii
Cei doi parametri avand
variatii armonice, lor li se pot asocia fazori corespunzatori, iar in
figura 46 sunt reprezentati fazorii ![]() intr-un plan complex (+1, +j), evidentiindu-se si
unghiul αs.
intr-un plan complex (+1, +j), evidentiindu-se si
unghiul αs.
Fazorii ![]() se rotesc cu viteza
unghiulara ω in jurul originii lor (au aceeasi pulsatie
ω) si atunci proiectiile lor, in orice moment, pe axa reala
vor da valorile instantanee ale fluxului magnetic respectiv, respectiv ale
t.e.m.
se rotesc cu viteza
unghiulara ω in jurul originii lor (au aceeasi pulsatie
ω) si atunci proiectiile lor, in orice moment, pe axa reala
vor da valorile instantanee ale fluxului magnetic respectiv, respectiv ale
t.e.m.
Fig.2.46 Fazorii
![]() si
si ![]()
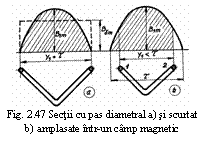
![]() , (51)
, (51)
iar "in fazorial" aceasta relatie se poate nota
![]() ,
,
in care (-j)este operatorul de
rotire cu π/2 "in urma" (semnul - !) fazorului ![]() asa cum s-a
aratat anterior.
asa cum s-a
aratat anterior.
Pe de alta parte, t.e.m. indusa intr-o sectie depinde de o anumita geometrie a sectiei respective. Astfel, daca sectia are un pas diametral, adica, y1=τ asa cum se arata in figura 47a, atunci fluxul magnetic de armonica 1 (numita armonica fundamentala), ce se inlantuie cu sectia respectiva este dat de relatia:
![]() , (52)
, (52)
in care ![]() este inductia medie din intrefier (adica este
inaltimea dreptunghiului care are lungimea y1=τ si suprafata
delimitata de sinusoida - fig. 47a) care se determina cu
relatia:
este inductia medie din intrefier (adica este
inaltimea dreptunghiului care are lungimea y1=τ si suprafata
delimitata de sinusoida - fig. 47a) care se determina cu
relatia:
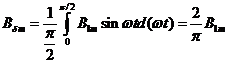
iar S=la τ este suprafata activa a sectiei, adica suprafata strabatuta de liniile campului magnetic, respectiv cea delimitata de lungimea activa a sectiei la si latimea y1=τ.T.e.m. indusa intr-un conductor de lungimea la poate fi notata sub forma
![]()
daca acest conductor taie liniile unui camp magnetic cu variatie armonica. Amplitudinea acestei t.e.m. este
![]() ,
,
iar daca se tine seama ca
![]()
pentru ca τ= D/2p (D, este diametrul unui rotor ca viteza periferica v, la exteriorul caruia se amplaseaza conductorul), adica
![]() , (53)
, (53)
iar valoarea efectiva a acestei t.e.m. este
![]() . (54)
. (54)
B. Determinarea coeficientului de scurtare
Pentru o sectie cu pas scurtat (y1< τ), asa cum se arata in figura 47b, fluxul magnetic ce se inlantuie cu sectia respectiva este mai mic, pentru ca suprafata activa a sectiei este mai mica: S=lay1 , cu y1< τ si deci se poate nota:
![]() (55)
(55)
in care ks este coeficientul de scurtare, subunitar in acest caz, cu ajutorul caruia se va tine seama ca t.e.m. indusa intr-o astfel de sectie este mai mica decat t.e.m. indusa, in aceleasi conditii, intr-o sectie cu pas diametral; cu alte cuvinte t.e.m. indusa intr-o sectiune cu pas scurtat Es' va fi egala cu t.e.m. indusa intr-o sectie cu pas diametral Es, inmultita cu coeficientul de scurtare ks.
Cum se poate determina acest coeficient de scurtare?
La folosirea unui pas principal scurtat se poate defini asa-numitul pas principal relativ (prin raportarea lui y1 la pasul polar)
![]() , (56)
, (56)
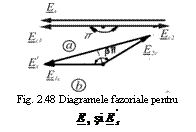 care este evident subunitar si
adimensional. Daca se tine seama de acest element, atunci fazorii
t.e.m.
care este evident subunitar si
adimensional. Daca se tine seama de acest element, atunci fazorii
t.e.m. ![]() induse in cei doi
conductori ai spirei cu pas scurtat (fig. 47 b), au acelasi modul (pentru
ca au aceeasi lungime activa la , aceeasi
viteza v etc), dar nu se gasesc in antifaza (adica
defazati cu π), ci sunt defazati cu unghiul βπ,
asa cum apare in figura 48. Atunci valoarea Es' t.e.m.
in modul este
induse in cei doi
conductori ai spirei cu pas scurtat (fig. 47 b), au acelasi modul (pentru
ca au aceeasi lungime activa la , aceeasi
viteza v etc), dar nu se gasesc in antifaza (adica
defazati cu π), ci sunt defazati cu unghiul βπ,
asa cum apare in figura 48. Atunci valoarea Es' t.e.m.
in modul este
![]() (57)
(57)
iar in cazul spirei cu pasul principal diametral este
![]() .
.
Coeficientul de scurtare rezulta din raportarea modulelor t.e.m. corespunzatoare celor doua cazuri:
![]() (58)
(58)
Relatia din (58) este valabila pentru coeficientul de scurtare cand se ia in considerare numai armonica fundamentala a campului magnetic (adica este ks1), in cazul armonicii superioare de ordinul υ a campului magnetic avem
![]() . ( 58a)
. ( 58a)
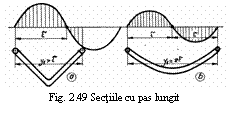 In practica se constata
ca pentru un pas principal scurtat
In practica se constata
ca pentru un pas principal scurtat ![]() (o scurtare cu circa 20%), rezulta ks1=0,95,.,0,98
adica amplitudinea t.e.m. indusa scade cu circa 5,, 2%.Pe de
alta parte, este posibil ca o spira (sau sectie) sa se
execute, cu pasul principal lungit (y1> τ); in acest caz se
lungesc capetele frontale ale spirei (sectie)(deci portiunile
neactive ale spirei), adica creste consumul conductoarelor de cupru
(aluminiu), dar coeficientul ks1 ramane tot subunitar, pentru
ca fluxul rezultant, care strabate suprafata activa a
spirei (sectiei) scade asa cum se vede din figura 49a. Pentru cazul
din figura 49b, fluxul magnetic ce strabate suprafata activa a
spirei este nul si deci ks1=0.
(o scurtare cu circa 20%), rezulta ks1=0,95,.,0,98
adica amplitudinea t.e.m. indusa scade cu circa 5,, 2%.Pe de
alta parte, este posibil ca o spira (sau sectie) sa se
execute, cu pasul principal lungit (y1> τ); in acest caz se
lungesc capetele frontale ale spirei (sectie)(deci portiunile
neactive ale spirei), adica creste consumul conductoarelor de cupru
(aluminiu), dar coeficientul ks1 ramane tot subunitar, pentru
ca fluxul rezultant, care strabate suprafata activa a
spirei (sectiei) scade asa cum se vede din figura 49a. Pentru cazul
din figura 49b, fluxul magnetic ce strabate suprafata activa a
spirei este nul si deci ks1=0.
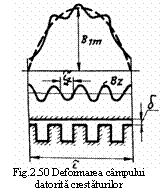 Si
totusi campul magnetic in intrefierul unei masini nu are o
variatie sinusoidala, adica in afara de armonica
fundamentala exista si unele armonice superioare a caror
amplitudine poate fi destul de mare. Aceste armonici superioare ale campului
apar din mai multe motive dintre care cele mai principale sunt:
Si
totusi campul magnetic in intrefierul unei masini nu are o
variatie sinusoidala, adica in afara de armonica
fundamentala exista si unele armonice superioare a caror
amplitudine poate fi destul de mare. Aceste armonici superioare ale campului
apar din mai multe motive dintre care cele mai principale sunt:
a) - distributia nesinusoidala a f.m.m. pe periferia interioara (exterioara) a statorului/rotorului;
b) - existenta crestaturilor si dintilor statorici / rotorici (figura 50);
c) - saturatia magnetica ce se produce pe anumite portiuni ale circuitelor magnetice ale masinii.
Existenta armonicelor superioare ale campului si deci inducerea unor t.e.m. de armonica superioara in infasurarile masinilor electrice produce unele neajunsuri pentru eliminarea carora se iau masuri inca din faza de proiectare a masinii electrice. Una dintre aceste masuri este folosirea pasului principal scurtat cu un anumit coeficient de scurtare, care duce la o micsorare oarecare a amplitudinii armonicii fundamentale a t.e.m. induse, dar poate duce si la scadere pronuntata a amplitudinilor armonicilor superioare ale t.e.m. induse.
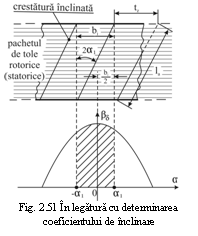
C. Determinarea coeficientului de inclinare.
O alta masura ce se ia pentru a micsora influenta armonicilor superioare este aceea a inclinarii crestaturilor in raport cu generatoarea cilindrului drept statoric si/sau rotoric.
In figura 51 este evidentiat pachetul de tole rotorice (statorice) in care sunt executate crestaturi inclinate cu pasul de inclinare bi (tz este pasul de crestatura sau pasul dentar).
La pasul de inclinare bi (de regula ales astfel incat sa anuleze sau sa micsoreze cat mai mult o anumita armonica superioara a t.e.m. induse, de exemplu es )rezulta unghiul 2α1 in raport cu crestatura neinclinata. Daca inductia din intrefier variaza armonic (cosinusoidal, asa cum se arata in partea inferioara a figurii 51), atunci t.e.m. indusa intr-o latura a sectiei, montata intr-o crestatura inclinata si de lungime activa la , este
![]() , (60 a)
, (60 a)
in care v este viteza periferica a
crestaturi, iar ![]() este valoarea medie a inductiei magnetice din intrefier
corespunzatoare crestaturii inclinate. Aceasta inductie
este
este valoarea medie a inductiei magnetice din intrefier
corespunzatoare crestaturii inclinate. Aceasta inductie
este
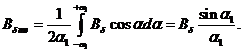 (60b)
(60b)
Din (60 a) si (60 b) rezulta
![]() ,
, ![]() (60c)
(60c)
iar in lipsa inclinarii avem
![]() . (60 d)
. (60 d)
Efectul inclinarii (care micsoreaza t.e.m. indusa) se poate lua in considerare prin coeficientul (factorul) de inclinare
![]() . (60e)
. (60e)
Daca se tine seama ca pentru distanta τ luata pe periferia interioara (exterioara) a statorului (rotorului) corespund π radiani electrici, atunci pentru bi vom avea 2α1 radiani electrici din care rezulta
![]() ,
,
dar pentru ca τ D/2p=ztz/2p ( z este numarul de dinti statorici/ rotorici), atunci
![]()
respectiv
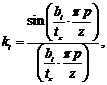 (60)
(60)
in care coeficientul ki este prezentat in functie de unii parametrii de proiectare ai masinii.
Pentru armonica superioara de ordinul υ avem:
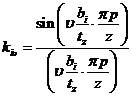 . (60a)
. (60a)
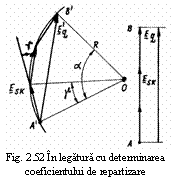 Daca bi este egal cu tz,
atunci
Daca bi este egal cu tz,
atunci ![]() , dar pentru
armonicile superioare kiν are valori destul de mici, adica
pentru cazul dat, amplitudinea armonicii fundamentale (de ordinul 1) a t.e.m.
induse se reduce relativ putin la inclinarea crestaturilor, pe cand
amplitudinea armonicilor superioare a t.e.m. induse scade mult. Dar prin
inclinarea crestaturilor se mareste lungimea spirei ceea ce duce
la cresterea rezistentei sale ohmice si a reactantei de
dispersie.
, dar pentru
armonicile superioare kiν are valori destul de mici, adica
pentru cazul dat, amplitudinea armonicii fundamentale (de ordinul 1) a t.e.m.
induse se reduce relativ putin la inclinarea crestaturilor, pe cand
amplitudinea armonicilor superioare a t.e.m. induse scade mult. Dar prin
inclinarea crestaturilor se mareste lungimea spirei ceea ce duce
la cresterea rezistentei sale ohmice si a reactantei de
dispersie.
D. Determinarea coeficientului de repartizare
Intr-o alta ordine de idei, trebuie remarcat faptul ca schemele infasurarilor masinilor se alcatuiesc astfel incat campul magnetic produs in interfierul masinii, sa fie cat mai apropiat de o variatie armonica. In aceasta idee, infasurarile masinilor se formeaza din grupe de sectii (bobine) definindu-se parametrul q ce reprezinta numarul de crestaturi pe pol si faza, iar daca se ia in considerare o infasurare in dublu strat rezulta ca este vorba de fapt de q sectii pe pol si faza, legate intre ele in serie dar dispuse in q crestaturi vecine. T.e.m. indusa in aceste sectii, distribuite pe q crestaturi, nu este egala cu suma aritmetica a t.e.m., in fiecare sectie (desi sectiile sunt legate in serie intre ele), ci cu suma geometrica a t.e.m. respective pentru ca sectiile sunt dispuse in crestaturi statorice/rotorice care sunt decalate spatial intre ele (deci si cu campul magnetic al armonicii fundamentale) cu unghiul la centru g /mq, asa cum apare si in figura 5Dar in acest fel t.e.m. totala |Eq'| indusa in grupul de sectii, format din q sectii inseriate dar repartizate pe q perechi de crestatura, va fi mai mica decat t.e.m. |Eq| indusa in aceleasi q sectii daca ele toate ar fi montate intr-o singura pereche de crestaturi.
Coeficientul de repartizare kr (repartizare a q sectii pe q perechi de crestaturi) simuleaza acest efect al micsorarii si se defineste prin raportul :
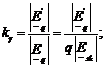 (61)
(61)
el este subunitar si tine seama de efectul repartizarii sectiilor pe mai multe perechi de crestaturi. Din figura 52 rezulta :
![]()
iar conform cu (61) se obtine pentru o infasurare m - fazata
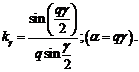 (62)
(62)
Din (62)
avem : pentru q=1, kr =1 pentru q>1, kr<1, cu
precizarea ca pentru ![]() rezulta
rezulta
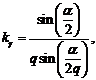 (63)
(63)
adica in acest caz kr
este dat de raportul dintre coarda A'B' si arcul de cerc AB. Pentru
un α dat, kr∞ va fi deci cea mai mica valoare a lui
kr. In practica, in mod obisnuit, se ia q=2,.,12
astfel incat kr este putin mai mic decat 1, adica
amplitudinea armonicii fundamentale a t.e.m. va scadea putin, in
schimb amplitudinea armonicelor superioare a t.e.m. induse va scadea in
mod pronuntat. Expresia coeficientului de repartizare pentru o
armonica superioara de ordinul ![]() este
este
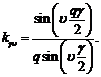 (63a)
(63a)
E. T.e.m. indusa in infasurarea unei faze a masinii si armonicele sale superioare
Daca t.e.m. indusa intr-un conductor, conform cu (53) este
![]()
atunci t.e.m. indusa intr-o spira va fi
![]() (64)
(64)
daca pasul principal al spirei este y1= τ.
Pentru o sectie cu ws spire, t.e.m. indusa va fi
![]()
daca y1= τ. Pentru un grup de q sectii, repartizate pe q crestaturi, t.e.m. indusa este:
![]()
Daca crestaturile sunt inclinate, atunci trebuie luat in considerare coeficientul de inclinare ki , iar daca pasul principal al sectiilor nu este diametral, de exemplu y1< τ atunci se ia in evidenta si coeficientul de scurtare ks, adica
![]()
Produsul coeficientilor ks ki kr= kw se numeste coeficientul (factorul) de infasurare, respectiv avem
![]()
Dar B1m= πBδm/2 si atunci
![]() (65)
(65)
Insa
![]() este fluxul magnetic
ce inlantuie grupul de sectii considerat si deci
este fluxul magnetic
ce inlantuie grupul de sectii considerat si deci
![]()
Daca in infasurarea unei faze a masinii electrice exista n grupuri de q sectii, atunci:
![]()
Dar nqws=w reprezinta numarul total de spire corespunzator infasurarii unei faze a masinii, deci:
![]() (66)
(66)
adica t.e.m. indusa in
infasurarea unei faze este proportionala cu numarul de
spire al fazei (![]() se denumeste numarul efectiv de spire), cu
frecventa campului magnetic si cu fluxul campului magnetic.
se denumeste numarul efectiv de spire), cu
frecventa campului magnetic si cu fluxul campului magnetic.
Uneori pentru determinarea t.e.m. indusa intr-o infasurare a unei faze la o masina m - fazata se foloseste diagrama fazoriala a grupei de sectii denumita steaua t.e.m. de crestatura.
In figura 53 este dat un exemplu pentru o astfel de diagrama fazoriala cu urmatoarele date principale:
m=3; p=1; q=
Pentru a
trasa steaua t.e.m. de crestatura (de sectie), asa cum este
aratat in figura 53 a, se figureaza o stea cu 2p.m.q1
(adica 3.2=12) raze egale (pentru ca modulele t.e.m. induse sunt
egale) cu un unghi intre ele ![]() . De altfel aceasta diagrama permite determinarea
coeficientului de repartizare kr pentru infasurarile
simetrice sau nesimetrice, bifazice sau m fazice.
. De altfel aceasta diagrama permite determinarea
coeficientului de repartizare kr pentru infasurarile
simetrice sau nesimetrice, bifazice sau m fazice.
In
diagrama din steaua t.e.m. de crestatura se stabilesc inceputurile
si sfarsiturile de faza in functie de y1,
decalajul intre inceputurile fazelor, iar in final se "construieste
geometric" (facand mai intai o miscare de translatie pentru
fazorii Es1 , Es2 astfel incat punctul de
sfarsit al unui fazor sa devina punctul de inceput al celuilalt
fazor) fazorul t.e.m. rezultante induse in faza A. Fazorul ![]() va fi defazat (in mod
evident) cu 2π/3 radiani in raport cu fazorul
va fi defazat (in mod
evident) cu 2π/3 radiani in raport cu fazorul ![]() etc.
etc.
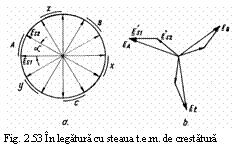 Pentru a stabili expresia t.e.m. corespunzatoare
armonicii superioare de ordinul ν, se reia relatia generala a
t.e.m. pentru armonica fundamentala (de ordinul1) din relatia (66)
si se tine seama de parametrii modificabili respectivi, avem:
Pentru a stabili expresia t.e.m. corespunzatoare
armonicii superioare de ordinul ν, se reia relatia generala a
t.e.m. pentru armonica fundamentala (de ordinul1) din relatia (66)
si se tine seama de parametrii modificabili respectivi, avem:
![]() (67)
(67)
Aici avem
![]() , (68)
, (68)
in care f1=50Hz este frecventa standard , respectiv
![]() (69)
(69)
in care coeficientii de scurtare, inclinare si repartizare pentru armonica de ordinul ν au fost precizati in cele anterioare. Tot la fel avem:
![]() (70)
(70)
in care
![]() (71)
(71)
unde τ1= este pasul polar stabilit anterior, iar Bδmν este inductia din interfierul masinii corespunzatoare armonicii de ordinul ν al campului magnetic rezultant. Daca se tine seama de cele anterioare, atunci se poate nota:
![]() (72)
(72)
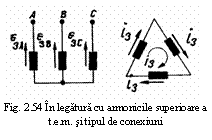 Deci in cazul general, intr-o
infasurare a unei faze se vor induce t.e.m.: E1,E3,E5,
respectiv vom avea
Deci in cazul general, intr-o
infasurare a unei faze se vor induce t.e.m.: E1,E3,E5,
respectiv vom avea ![]() (73)
(73)
adica oricum E>E1, iar asta inseamna:
a) - pierderi suplimentare de natura electrica si magnetica in masina;
b) - parametrii energetici (factor de putere, randament, etc) mai scazuti.
Existenta armonicelor superioare depinde si de conexiunile infasurarilor.
In sisteme trifazate conexiunile cele mai utilizate sunt steaua si triunghiul, iar in cazul sistemelor multifazice avem multistea si multiunghi. In sistemul trifazat insa o importanta mai deosebita o are armonica a 3-a si multiplele ei impare , dupa cum intr-un sistem 5-fazat o importanta mai deosebita o are armonica a 5-a si multiplele sale impare si asa mai departe.
Pe de alta parte, intr-un sistem trifazat in fazele A, B, C armonicele fundamentale sunt defazate intre ele cu 1200, iar t.e.m. ale armonicelor multiple (impare) de 3 in aceleasi faze A, B, C se gasesc in faza si la conexiunea stea la tensiunile de linie aceste armonici nu apar - figura 54. La conexiunea triunghi, t.e.m. ale armonicelor multiplu (impare) de trei se aduna si formeaza un curent de circulatie (care circula in infasurari). Aceste aspecte trebuie luate in considerare la proiectarea masinilor, avand in vedere ca armonicele superioare inrautatesc caracteristicile energetice ale masinilor, ori armoniciile superioare nu se produc numai la masini electrice ideale in intrefierul carora exista un camp magnetic invartitor circular.
Existenta armonicelor superioare depinde si de conexiunile infasurarilor.
In sisteme trifazate conexiunile cele mai utilizate sunt steaua si triunghiul, iar in cazul sistemelor multifazice avem multistea si multiunghi. In sistemul trifazat insa o importanta mai deosebita o are armonica a 3-a si multiplele ei impare , dupa cum intr-un sistem 5-fazat o importanta mai deosebita o are armonica a 5-a si multiplele sale impare si asa mai departe.
Pe de alta parte, intr-un sistem trifazat in fazele A, B, C armonicele fundamentale sunt defazate intre ele cu 1200, iar t.e.m. ale armonicelor multiple (impare) de 3 in aceleasi faze A, B, C se gasesc in faza si la conexiunea stea la tensiunile de linie aceste armonici nu apar - figura 54. La conexiunea triunghi, t.e.m. ale armonicelor multiplu (impare) de trei se aduna si formeaza un curent de circulatie (care circula in infasurari). Aceste aspecte trebuie luate in considerare la proiectarea masinilor, avand in vedere ca armonicele superioare inrautatesc caracteristicile energetice ale masinilor, ori armoniciile superioare nu se produc numai la masini electrice ideale in intrefierul carora exista un camp magnetic invartitor circular.
9. Fortele magnetomotoare (f.m.m.) produse de infasurari
A. Deducerea relatiilor principale pentru f.m.m.
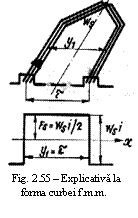 Campul magnetic dintr-o
masina electrica se produce cu ajutorul curentului electric care
circula prin infasurarile masinii. Daca se admite
faptul ca:
Campul magnetic dintr-o
masina electrica se produce cu ajutorul curentului electric care
circula prin infasurarile masinii. Daca se admite
faptul ca:
a) - intrefierul masinii δ este mic in raport cu diametrul rotorului si cu pasul polar;
b) - miezul magnetic al masinii este nesaturat,
atunci forma curbei de variatie a campului magnetic este
data de forma curbei f.m.m. Daca se considera o sectie
cu ws spire, cu pasul diametral (y1=τ),
parcursa de curentul ![]() (fig. 55), atunci f.m.m. produsa de
aceasta sectie este:
(fig. 55), atunci f.m.m. produsa de
aceasta sectie este:
![]()
respectiv
![]() (74)
(74)
in care
![]()
si s-a tinut seama ca bobina are 2 poli magnetici (un N si un S), adica p=1. Curba f.m.m. apare sub forma unui dreptunghi (pentru un t dat), adica sub forma unei unde dreptunghiulare cu amplitudinea iws Aceasta variatie dreptunghiulara poate fi insa descompusa intr-o serie Fourier si retinuta armonica fundamentala a acesteia.
O forma de unda dreptunghiulara (precum cea din figura 55) poate fi definita, conform cu figura 55a, in cazul general astfel:
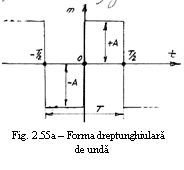
![]()
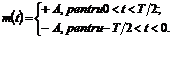
si ![]() (in cazul dat
(in cazul dat ![]() ).
Conform cu definitia anterioara, functia
).
Conform cu definitia anterioara, functia ![]() este
simetrica in raport cu originea sistemului de axe (adica
antisimetrica si deci impara, respectiv seria sa Fourier nu va
contine armonici pare si nici termeni in cosinus). Pentru
coeficientii seriei Fourier se poate deci nota:
este
simetrica in raport cu originea sistemului de axe (adica
antisimetrica si deci impara, respectiv seria sa Fourier nu va
contine armonici pare si nici termeni in cosinus). Pentru
coeficientii seriei Fourier se poate deci nota:
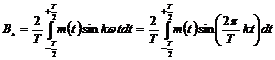
in care s-a avut in vedere ca ![]() si
deci
si
deci ![]() .
Expresia anterioara se mai poate prelucra succesiv astfel:
.
Expresia anterioara se mai poate prelucra succesiv astfel:
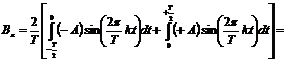
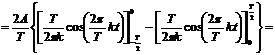
![]()
Din (75) se vede ca pentru k=2p
(deci k par), avem ![]() ,
iar pentru
,
iar pentru ![]() ,
(deci k impar) rezulta:
,
(deci k impar) rezulta:
![]() ,
,
respectiv pentru armonica fundamentala (adica k=1) avem:
![]()
asa cum este evidentiat si in figura 55b.
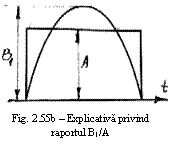 Deci, pentru o forma de unda
dreptunghiulara a f.m.m. precum cea din (74), rezulta ca aceasta
poate fi pusa sub forma unei serii Fourier de forma:
Deci, pentru o forma de unda
dreptunghiulara a f.m.m. precum cea din (74), rezulta ca aceasta
poate fi pusa sub forma unei serii Fourier de forma:
![]()
care cuprinde armonici impare variabile in timp (factorul cosωt) si in spatiu (factorul cosνα) si unde
![]() respectiv
respectiv![]()
expresii ce tin seama si de relatia (76), respectiv (77).
Un alt caz este acela al f.m.m. produsa de doua bobine (a caror
grosimile laturilor de ducere si de intoarcere nu pot fi neglijabile) cu
pas scurtat ![]() ;aceasta poate fi prezentata sub
forma unei unde trapezoidale asa cum apare in figura 56. Aceasta
forma de unda, descompusa intr-o serie Fourier, conduce la
amplitudini mai mici ale armonicelor superioare, decat forma de unda
dreptunghiulara
;aceasta poate fi prezentata sub
forma unei unde trapezoidale asa cum apare in figura 56. Aceasta
forma de unda, descompusa intr-o serie Fourier, conduce la
amplitudini mai mici ale armonicelor superioare, decat forma de unda
dreptunghiulara
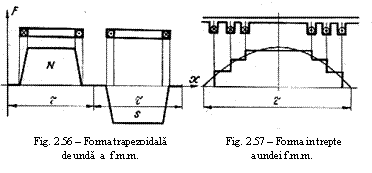 F.m.m. produsa de un grup de
sectii distribuite pe q crestaturi, conduce la o forma in trepte
a undei, asa cum se arata in figura 57. Descompunerea intr-o serie
Fourier a acestei forme in trepte, aduce o micsorare mai
pronuntata decat a cazului precedent a amplitudinilor armonicelor
superioare.
F.m.m. produsa de un grup de
sectii distribuite pe q crestaturi, conduce la o forma in trepte
a undei, asa cum se arata in figura 57. Descompunerea intr-o serie
Fourier a acestei forme in trepte, aduce o micsorare mai
pronuntata decat a cazului precedent a amplitudinilor armonicelor
superioare.
Din aceasta prezentare se poate remarca ca folosirea unor infasurari cu pas scurtat si distribuite pe mai multe crestaturi conduce la o micsorare substantiala a amplitudinilor armonicelor superioare ale campului.
Pe de alta parte, f.m.m. corespunzatoare unei infasurari a unei faze a masinii va fi egala cu suma f.m.m. a grupelor de sectii care fac parte din faza respectiva.
B. Determinarea f.m.m. rezultante.
Daca se considera cazul unei
infasurari m-fazate, formata din m
infasurari identic asezate pe o armatura
statorica/rotorica, astfel incat axele lor sa fie decalate in
spatiu cu unghiul electric ![]() ,respectiv
un unghi geometric
,respectiv
un unghi geometric![]() si parcurse de un sistem m-fazat de curenti:
si parcurse de un sistem m-fazat de curenti:
![]() (80)
(80)
atunci f.m.m. produse de cele m infasurari vor fi:
![]()
![]()
![]()
in care, corespunzator cu (79) avem:
![]()
iar![]() este
coeficientul de infasurare corespunzator γ-armonicii.
este
coeficientul de infasurare corespunzator γ-armonicii.
Daca ne bazam pe relatia trigonometrica:
![]() (83)
(83)
atunci f.m.m. de indice k poate fi notata sub forma :
![]()
![]() (84)
(84)
Din (84) se poate observa imediat ca Fk este formata din 2 unde:
o unda directa (de dreapta), care se roteste in "sensul
dreapta" ![]() ;
;
o unda inversa (de stanga), care se roteste in "sensul
stanga"![]() .
.
F.m.m. rezultanta este:
![]()
![]() (85)
(85)
care prin inversarea semnelor de sumare duce la expresia:
![]()
![]()
Pentru γ=1 se obtine armonica fundamentala a f.m.m. rezultante:
![]() (87)
(87)
Primul termen al
expresiei din (87) nu depinde de m, adica undele directe (cu rotire
"sensul dreapta") sunt in faza si suma lor este 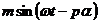 .
Undele inverse sunt defazate intre ele cu unghiul electric
.
Undele inverse sunt defazate intre ele cu unghiul electric ![]() si suma lor este evident nula. Deci
expresia precedenta se poate nota sub forma:
si suma lor este evident nula. Deci
expresia precedenta se poate nota sub forma:
![]() , (88)
, (88)
din care rezulta ca unda f.m.m. rezultanta de armonica fundamentala, este o unda invartitoare circulara directa Expresia din (88) se poate particulariza pentru m=3.
![]() (89)
(89)
C. Armonicele superioare ale f.m.m
Daca se revine la cazul general m-fazat si se iau in considerare armonicele multiple de m: γ=mM, cu M=1,2,, atunci conform cu (86) avem:
![]()
![]()
![]() (90)
(90)
care poate fi notata sub forma:
![]()
![]()
din care se deduce ca rezultanta armonicilor multiple de m este
nula, avand in vedere ca undele directe si inverse formeaza
sisteme defazate intre ele cu unghiul electric 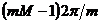 ,
respectiv
,
respectiv 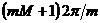 a caror suma este nula.
a caror suma este nula.
Similar pentru armonicile impare de
ordinul ![]() (in cazul trifazat cu m=3, avem γ=7, 13,
19, ), din relatia (86) rezulta:
(in cazul trifazat cu m=3, avem γ=7, 13,
19, ), din relatia (86) rezulta:
![]()
![]()
din care se poate observa ca undele inverse, formand un sistem simetric, suma lor este nula, iar undele directe sunt in faza si deci se obtine rezultanta:
![]() (91)
(91)
De asemenea, pentru armonicele impare
de ordinul ![]() (pentru cazul trifazat cu m=3, avem
(pentru cazul trifazat cu m=3, avem ![]() ),
din
),
din
![]()
![]() , (92)
, (92)
din care rezulta ca in acest caz undele directe formeaza un sistem simetric a caror sursa este nula, iar undele inverse sunt in faza si deci avem:
![]() (93)
(93)
Pe baza acestor concluzii, in figura 58 sunt prevazute graficele f.m.m. pentru armonica fundamentala, de ordinul 5 si 7 pentru mai multe momente succesive:cu IA=Imax, IB=Imax, IC=Imax; infasurarea este trifazata cu q=1 crestatura/pol si faza.
Din figura 58 se observa ca armonica fundamentala (care are o amplitudine mult mai mare decat armonicile superioare) se deplaseaza in sensul succesiunii fazelor pe periferia armaturii statorice, rotorice si intr-o perioada a curentului parcurge numai 1/p dintr-o rotatie.
Armonica de ordinul 3 fiind o unda inversa se deplaseaza in sens invers in raport cu armonica fundamentala, iar armonica de ordinul 7 este o unda directa si se deplaseaza in acelasi sens cu armonica fundamentala.
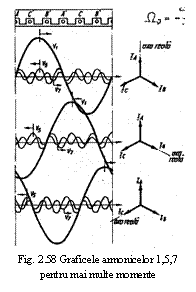
D. Graficul f.m.m. rezultante
Unul dintre subiectele importante este
cel legat de obtinerea f.m.m. rezultante pentru o infasurare
data. In figura 59 sunt prezentate elementele legate de obtinerea
f.m.m. rezultante pentru momentul cand in faza A curentul are valoarea
maxima IA=Im, iar in celelalte doua faze avem ![]() .
Infasurarea considerata are urmatorii parametrii: m=3;
2p=4; q=2; z=24; y1=5; τ=6 (deci y1< τ).
.
Infasurarea considerata are urmatorii parametrii: m=3;
2p=4; q=2; z=24; y1=5; τ=6 (deci y1< τ).
Se poate proceda dupa urmatoarea metodologie:
se determina toti parametrii necesari pentru a trasa steaua t.e.m. de crestatura;
se traseaza steaua t.e.m. de crestatura;
se executa schema desfasurata a infasurarilor, tinand seama de steaua t.e.m. de crestatura si ceilalti parametrii ai infasurarii;
in acest fel in toate cele 24 de
crestaturi ale infasurarii, se cunosc acum laturile din
cele doua straturi carei faze apartin si ce fel de laturi
sunt: de ducere sau de intoarcere; pentru a evidentia aceste aspecte se
stabilesc niste simboluri distincte pentru cele trei faze, asa cum se
face in figura 59, si niste simboluri distincte (![]() )
pentru laturile de ducere si de intoarcere;
)
pentru laturile de ducere si de intoarcere;
se admite ca la momentul considerat avem, de exemplu, IA=Im, iar IB=IC=Im/2;
conform cu cele anterioare se traseaza graficul curentilor din crestatura, respectiv al f.m.m. rezultante asa cum este prezentat in figura 59;
se ia in considerare o alta stare a curentilor din cele trei faze ale masinii si se reiau eventual graficele curentilor si f.m.m. etc.
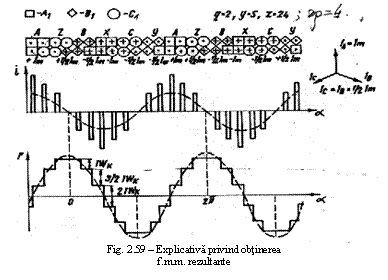 Se poate constata ca forma graficului f.m.m. depinde de parametrii
infasurarii, dar ea se apropie de o forma sinusoidala
cand q creste, iar scurtarea pasului principal este
Se poate constata ca forma graficului f.m.m. depinde de parametrii
infasurarii, dar ea se apropie de o forma sinusoidala
cand q creste, iar scurtarea pasului principal este ![]() . Insa, o forma strict sinusoidala a graficului f.m.m. se
poate obtine numai in cazul unei distributii sinusoidale a
infasurarii pe periferia armaturii magnetice, ceea ce se poate obtine numai la
unele masinii electrice speciale.
. Insa, o forma strict sinusoidala a graficului f.m.m. se
poate obtine numai in cazul unei distributii sinusoidale a
infasurarii pe periferia armaturii magnetice, ceea ce se poate obtine numai la
unele masinii electrice speciale.
In cazul infasurarilor cu o fractionare a lui q, se obtine o curba nesimetrica pentru f.m.m. si aceasta poate fi diferita chiar pentru diversele perechi de poli ale masinii.
10. CUPLUL ELECTROMAGNETIC AL MASINILOR ELECTRICE
A. Valoarea instantanee a cuplului electromagnetic
Se admite o masina electrica formata din doua armaturi feromagnetice considerand si anumite ipoteze simplificatoare:
- armaturile sunt netede;
- intrefierul este constant;
- caracteristica magnetica a armaturilor este liniara, iar permeabilitatea magnetica poate fi considerata infinita.
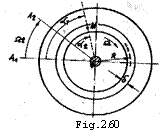 Fiecare armatura este
dotata cu curenti polifazati cu pulsatia ω1,
respectiv ω2 (indicele 1 se refera la stator, iar indicele
2 la rotor); numarul perechilor de poli sunt p1, respectiv p
Armaturile sunt mobile iar viteza unghiulara relativa dintre ele
este Ω si fiecare armatura produce un camp magnetic
invartitor cu inductiile:
Fiecare armatura este
dotata cu curenti polifazati cu pulsatia ω1,
respectiv ω2 (indicele 1 se refera la stator, iar indicele
2 la rotor); numarul perechilor de poli sunt p1, respectiv p
Armaturile sunt mobile iar viteza unghiulara relativa dintre ele
este Ω si fiecare armatura produce un camp magnetic
invartitor cu inductiile:
![]()
![]() (95)
(95)
Unghiurile α1 si α2 sunt coordonatele unghiulare ale unui punct M din intrefier - figura 60 - in raport cu axele de referinta OA1 si OA2 solidare cu statorul, respectiv rotorul masinii si ele indeplinesc relatia
![]() (96)
(96)
sensurile lor pozitive fiind indicate in figura.
Defazajele φ1, φ2 tin seama de valoarea inductiilor la t=0 si
Sistemul magnetic fiind considerat liniar, in acest caz se poate aplica principiul superpozitiei astfel incat campul magnetic rezultant este :
b = b1 +b2 (97)
Expresia cuplului electromagnetic instantaneu se obtine prin aplicarea teoremei fortelor generalizate (vezi capitolul 1) in conditiile fluxului magnetic constant, variabila fiind unghiul de defazaj dintre cele doua campuri
(98)
respectiv
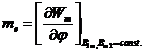 (99)
(99)
Deoarece permeabilitatea magnetica a armaturilor masinii este considerata infinita, energia magnetica se localizeaza numai in intrefierul masinii de marimea δ si atunci conform cu (1.40) avem:
![]()
in care:
![]()
iar volumul elementar in acest caz este ![]() respectiv
respectiv
![]() (100)
(100)
In (100) l este lungimea axiala a armaturilor, iar R este raza medie a intrefierului.
Conform cu (97), (95), relatia (100) devine
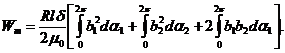 (101)
(101)
Expresiile lui b1 si b2 din (95) nu depind de φ si deci derivatele in raport cu φ ale primelor doua integrale din (101) sunt nule. Astfel, de exemplu, avem
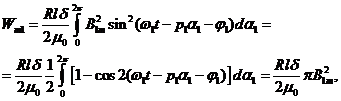
in care s-a tinut seama de relatia trigonometrica
![]()
Dar ![]() si un rezultat similar se obtine
pentru a doua integrala din (101).
si un rezultat similar se obtine
pentru a doua integrala din (101).
Pe de alta parte se poate nota
![]()
respectiv
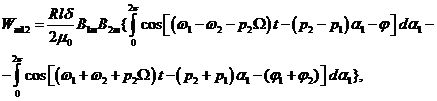 (102)
(102)
in care s-a tinut seama de relatia trigonometrica
![]()
Prima integrala din dreapta expresiei (102) poate fi diferita de zero numai daca
p1 - p2 = 0, respectiv p1 = p2 = p (103)
pentru ca numai in acest fel argumentul functiei trigonometrice de sub integrala nu mai depinde de parametrul α1. Dar pentru ca p1, p2 sunt numere naturale,rezulta ca cea de a doua integrala din (102) este mereu nula.
Din cele anterioare se desprinde prima concluzie: masinile electrice rotative cu camp magnetic invartitor pot produce un cuplu electromagnetic instantaneu numai in cazul in care armatura statorica cat si cea rotorica poseda acelasi numar de perechi de poli (p1 = p2 = p).
Cu aceasta concluzie (102) devine :
![]()
si conform cu (99) rezulta
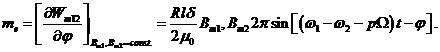 (104)
(104)
B. Valoarea medie a cuplului electromagnetic
Valoarea medie a cuplului electromagnetic pe o perioada
![]()
este
![]() (105)
(105)
Din (105) se observa imediat ca Me poate fi diferit de zero numai daca argumentul functiei trigonometrice de sub integrala nu depinde de t, adica
![]() (106)
(106)
respectiv
![]() (107)
(107)
in care ω este pulsatia relativa. Din (106) rezulta cea de a doua concluzie: in cadrul unei masini electrice rotative campurile magnetice invartitoare produse de armatura statorica si rotorica trebuie sa fie sincrone - respectiv
![]() , (108)
, (108)
adica sa fie imobile unul in raport cu celalalt.
Conform cu aceasta concluzie din (105) rezulta
![]() (109)
(109)
iar daca se tine seama de (106), atunci (104) devine
![]() (110)
(110)
adica valoarea instantanee a cuplului electromagnetic nu depinde de timp.
1 SPECTRUL INFINIT AL ARMONICELOR CAMPULUI DIN INTREFIERUL
MASINILOR ELECTRICE
Aproape intreaga energie a campului magnetic este concentrata in intrefierul masinilor electrice, de aceea pentru intelegerea fenomenelor legate de conversia electromagnetica a energiei este necesar sa se studieze cum se modifica forma campului magnetic din intrefier.
Camp magnetic circular exista numai la o masina ideala, iar in cadrul unei masini reale campul din intrefier este nesinusoidal si daca se cunoaste forma sa atunci, prin descompunere in serie Fourier se poate obtine (in afara de armonica fundamentala) intregul spectru de armonici superioare cu precizarea frecventelor si a amplitudinilor.
Sunt foarte multe cauze care determina producerea unui camp nesinusoidal in intrefierul masinilor, dar in general armonicele superioare ale campului se pot clasifica in doua grupe mari: armonici superioare temporale (de timp) si armonicile superioare spatiale.
Armonicele superioare temporale apar in intrefierul masinii mai ales datorita unor cauze exterioare masinii, iar cele spatiale se datoresc mai ales unor aspecte constructive ale masinii si neliniaritatii parametrilor sai.
S-a precizat deja ca o masina poate fi privita (figura 9) ca un cuadripol, iar daca se considera si "bornele termice" atunci ne apare ca un hexapol. De aceea armonicele superioare temporale pot apare in masina prin bornele electrice, mecanice si/sau termice ale acesteia.
Astfel, datorita nesinusoidalitatii tensiunii de alimentare (in cazul utilizarii convectoarelor sau a dispozitivelor cu semiconductoare) sau daca sistemul tensiunilor de alimentare este distorsionat, apar armonici superioare temporale in campul din intrefierul masinii. Daca tensiunea de alimentare contine o componenta continua, atunci in spectrul armonicilor apar si armonici pare.
Pe de alta parte, daca momentul static rezistent Mγ de la arborele masinii se modifica neliniar, atunci in intrefierul acesteia apar, de asemenea, armonici superioare temporale. Daca puterea masinii are acelasi ordin de marime cu puterea retelei la care este racordata, atunci in cazul unui soc de sarcina se poate produce distorsionarea tensiunii retelei cu aceleasi efecte.
Un soc termic poate produce aceleasi efecte vizand aparitia armonicilor superioare temporale in campul din intrefierul masinii; este adevarat insa ca in practica de regula masinile electrice nu sunt supuse unor socuri termice.
In ceea ce priveste armonicile superioare spatiale acestea sunt legate mai ales de distributia nesinusoidala a f.m.m, de neuniformitatea intrefierului datorata existentei crestaturilor statorice si rotorice, a formei conice sau eventual elipsoidale a intrefierului si a altor factori tehnologici.
Prin distribuirea infasurarilor pe crestaturi si prin scurtarea pasului se obtine o curba in trepte a f.m.m apropiata de o forma sinusoidala, dar care oricum nu este sinusoidala si prin descompunerea careia intr-o serie Fourier se obtin armonici superioare spatiale. Sensul de rotire al campurilor armonicilor superioare depinde si de numarul de faze din masina. Astfel, in cazul unor infasurari trifazate simetrice, apar armonicile superioare de ordinul ν=6n±1 (pentru n= 0,1,2, .,) dintre care cele de ordinul ν = 6n±1 (pentru n=0,1,2,.,) - adica 7,13,19,. - se rotesc cu o viteza de 7,13,19,. ori mai mica decat fundamentala dar in acelasi sens cu ea , iar cele de ordinul ν=6n-1 pentru n =1,2,.) - adica 5,11,17,. - se roteste cu o viteza de 5,11,17,. ori mai mica decat fundamentala si in sens invers acesteia.
In alta ordine de idei, existenta crestaturilor statorice si rotorice face ca intrefierul masinii sa fie neuniform, iar campul magnetic din intrefier este conditionat si de reluctanta magnetica a intrefierului, care nu este constanta de-a lungul statorului sau rotorului. In principiu deci curba inductiei din intrefier ar fi formata dintr-o armonica fundamentala si armonici superioare ale inductiei Bz corespunzatoare existentei crestaturilor. Amplitudinea acestor armonici depinde de marimea istmului de deschiderea al crestaturii (bi din figura 30) si de insasi marimea δ a intrefierului.
In cazul in care se considera si crestaturile statorice ca si cele rotorice configuratia campului se complica si mai mult: imaginea campului se poate aproxima prin existenta unor armonici superioare de crestaturi statorice in conditiile unui stator danturat si a unui rotor neted peste care se suprapun armonicele superioare de crestatura rotorice in conditiile unui rotor danturat si a unui stator neted. "Suprapunerea" aceasta (principiul superpozitiei) este posibila daca fierul masinii este nesaturat, daca insa apare si fenomenul saturatiei magnetice a fierului profilul campului din intrefier se complica si mai mult iar determinarea amplitudinilor armonicilor superioare de crestatura devine si mai dificila. O influenta asupra acestor amplitudini o are si numarul total de crestaturi in stator z1 si din rotor z2, iar cand ele se gasesc intr-un anumit raport, apar vibratii in masini si zgomote. La masini asincrone trifazate asemenea fenomene sunt pregnante pentru cazurile:
z1-z2=0,1,2,3,4; z1-z2=p, p=±1; z1=z2=2p, 2p ± 1, 2p± 1, 2p± 2, 2p±3;
2p±4; z1-z2=3p.
Pentru a micsora amplitudinea armonicelor de crestatura ale campului se practica inclinarea crestaturii cu un pas de crestatura, fapt care a fost prezentat intr-un paragraf anterior.
Din cele anterioare rezulta deci : alegand un anumit raport intre numarul crestaturilor statorice si rotorice, un anumit pas scurtat pentru infasurari, o anumita deschidere si inclinare a crestaturilor se poate micsora amplitudinea armonicelor superioare ale campului din intrefier, sau dimpotriva mari foarte mult amplitudinea unei anumite armonici superioare care devine astfel armonica de baza (fundamentala). Motoare care lucreaza pe o astfel de armonica de baza (superioara) se numesc reductoare si ele pot inlocui motoarele multipolare (deci cu turatie mica) sau suplini necesitatea reductoarelor de turatie.
Variatia neliniara a parametrilor masinii conduce, de asemenea, la formarea armonicelor superioare de camp in intrefierul masinii. Intr-o buna masura si factorii tehnologici legati de executia masinii au aceleasi efecte. Printre acesti factori se pot enumera excentricitatea rotorului in raport cu statorul si conicitatea rotorului.
Armonicele superioare ale campului magnetic din intrefierul masinii au in general influente negative asupra functionarii masinii inrautatind parametrii energetici ai masinii prin cresterea pierderilor din masina si prin producerea cuplurilor parazite. Acestea din urma vor fi prezentate in cadrul capitolului privind masina asincrona.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |