
Transformari de axe ale fazorilor spatiali
Fazorul spatial fiind definit in planul complex, expresia sa va depinde de axele acestui plan la care este raportat.
Considerand o axa de
referinta, in figura 1.7 s-au reprezentat doua sisteme de axe
bifazate a caror axa reala fac unghiurile 1,
respectiv 2 cu axa de referinta. In planul complex, ![]() fazorul se scrie:
fazorul se scrie:
![]() . (1.34)
. (1.34)
Acealsi
fazor, in planul ![]() are expresia:
are expresia:
![]() . (1.35)
. (1.35)
Trecerea de la sistemul 1 la 2, tinand seama de relatia (1.34) este:
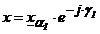 , (1.36)
, (1.36)
Introducand aceasta in relatia (1.35) rezulta:
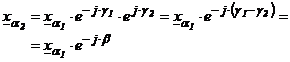 , (1.37)
, (1.37)
unde ![]() .
.
Daca planul complex este rotit in sens direct trigonometric cu unghiul , fazorul spatial raportat la planul rotit x2 este egal cu vechiul fazor x1 inmultit cu operatorul e-j.. x are argumentul x si unghiul 1, respectiv 2 fata de cele doua sisteme.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |