Notiuni fundamentale ale mecanicii teoretice.
Mecanica teoretica, clasica, studiaza doua aspecte particulare ale fenomenelor din natura: interactiunea mecanica si miscarea mecanica relativa a corpurilor si in care se fac o serie de ipoteze simplificatoare, care apar pe parcurs, la notiunea de care sunt legate.
Notiuni fundamentale: spatiul, timpul, masa, forta.
Diviziunile mecanicii: cinematica, dinamica, statica.
Principiile mecanicii clasice: principiul inertiei, principiul actiunii si reactiunii, principiul paralelogramului fortelor.
Momentul unui vector in raport cu un punct:
Fie
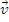 un vector legat, cu
punctul de aplicatie A. Se numeste momentul vectorului
un vector legat, cu
punctul de aplicatie A. Se numeste momentul vectorului
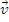 in
in
raport cu un punct O, numit pol, produsul vectorial dintre vectorul de pozitie al punctului
de aplicatie A al
vectorului si vectorul
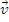 , adica:
, adica:
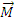
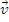
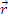 x
x
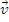 = O
= O
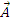 x
x
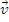
Proprietati ale momentului unui vector in raport cu un pol:
1. Modulul momentului unui vector in raport cu un pol este egal cu produsul dintre modulul
vectorului si distanta de la pol la suportul vectorului.
2. Momentul unui vector in raport cu un pol este nul daca vectorul este nul sau polul se afla
pe suportul vectorului.
3. Momentul unui vector in raport cu un pol nu se schimba atunci cand punctul de aplicatie al
vectorului se deplaseaza pe suportul sau.
4. Momentul unui vector in raport cu un alt pol O este egal cu suma dintre momentul
vectorului in raport cu polul initial O si produsul vectorial dintre vectorul de pozitie al
polului initial O in raport cu noul pol O si vectorul dat.
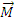 o'(
o'(
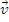
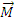
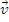 ) - O
) - O
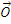 'x
'x
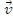
Momentul unui vector in raport cu o axa:
Se numeste momentul unui vector in raport cu o axa proiectia, pe acea axa, a momentului vectorului in raport cu un punct oarecare de pe axa.
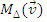
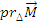
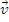
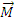
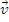
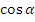
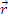 x
x
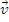
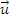
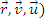
 o axa de
versor
o axa de
versor
Proprietati ale momentului unui vector in raport cu o axa:
1. Momentul unui vector in raport cu o axa nu se schimba daca punctul de aplicatie al
vectorului aluneca pe suportul sau.
2. Momentul unui vector nenul in raport cu o axa este nul, daca si numai daca axa si suportul
vectorului sunt coplanari.
Expresii analitice:
Momentul
unui vector
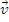 in raport cu o axa se
calculeaza cu formula :
in raport cu o axa se
calculeaza cu formula :
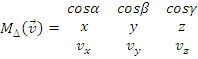 , unde
, unde
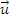 = cos
= cos
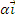 + cos
+ cos
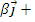 cos
cos
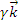
este
versorul axei
 ; A(x,y,z)
; A(x,y,z)
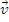
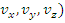 , A fiind punctul de
aplicatie al vectorului
, A fiind punctul de
aplicatie al vectorului
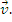
Torsorul unui sistem de vectori alunecatori:
Se considera un sistem de vectori alunecatori S = (
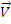 i
i
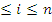 . Fata de un sistem cartezian de axe de coordonate Oxyz, din
spatiul euclidian tridimensional, vectorii sistemului se
caracterizeaza prin componentele lor (Xi, Yi, Zi).
. Fata de un sistem cartezian de axe de coordonate Oxyz, din
spatiul euclidian tridimensional, vectorii sistemului se
caracterizeaza prin componentele lor (Xi, Yi, Zi).
Se numeste vectorul rezultant al sistemului de
vectori S (rezultanta generala), notat cu
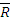 (S), suma vectorilor din
sistemul S. Acest vector
se poate obtine prin regula poligonului sau folosind teorema proiectiilor.
(S), suma vectorilor din
sistemul S. Acest vector
se poate obtine prin regula poligonului sau folosind teorema proiectiilor.
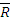 (S) =
(S) =
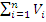
Se numeste vectorul moment rezultant al sistemului de vectori S,
in raport cu un punct O, notat cu
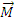 (S), vectorul egal cu suma momentelor vectorilor
sistemului in raport cu punctul O.
(S), vectorul egal cu suma momentelor vectorilor
sistemului in raport cu punctul O.
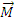 (S) =
(S) =
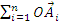 x
x
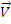 i
i
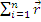 i x
i x
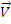 i
i
Ansamblul de
vectori (
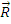 (S),
(S),
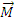 (S)), unde
(S)), unde
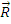 (S) este vectorul
rezultant al sistemului S, iar
(S) este vectorul
rezultant al sistemului S, iar
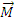 (S) - vectorul moment rezultant al sistemului de
vectori in raport cu polul O, se numeste torsorul sistemului S
in raport cu polul O si se noteaza cu
(S) - vectorul moment rezultant al sistemului de
vectori in raport cu polul O, se numeste torsorul sistemului S
in raport cu polul O si se noteaza cu
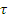 o(S):
o(S):
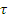 o(S) =
o(S) =
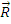 (S),
(S),
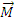 (S))
(S))
Invarianti ai unui sistem de vectori
Trinomul invariant al sistemului de vectori alunecatori.
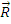 (S)
(S)
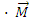 O'(S) =
O'(S) =
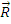 (S)
(S)

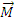 (S),
(S),
Doua sisteme de vectori alunecatori S si S , pentru care:
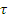 o(S) =
o(S) =
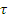 o(S') (
o(S') (
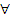 O), O - punct din
spatiu,
O), O - punct din
spatiu,
se numesc sisteme echivalente de vectori alunecatori.
Se
noteaza S
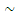 S'.
S'.
S
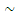 S'
S'
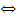
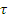 o(S) =
o(S) =
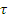 o(S'), (
o(S'), (
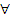 O).
O).
Sisteme echivalente de vectori alunecatori. Sisteme echivalente de forte.
Doua sisteme de forte sunt echivalente daca au acelasi efect mecanic in orice punct al solidului rigid.
Proprietati ale sistemelor echivalente de vectori:
Torsorul unui sistem de vectori este invariant fata de operatiile elementare de echivalenta.
Determinarea celui mai simplu sistem dintr-o clasa de echivalenta se numeste reducerea sistemului de vectori.
Convenim sa notam cu S0 sistemul care are
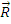 (S0)=0 si
(S0)=0 si
 O(S0)=0. Acest sistem se numeste sistem echivalent cu zero in O.
O(S0)=0. Acest sistem se numeste sistem echivalent cu zero in O.
Forta care actioneaza asupra unui solid rigid este un vector alunecator.
Teorema lui Varignon
Momentul vectorului rezultant al unui sistem de vectori concurenti in raport cu un punct O
este egal cu vectorul moment rezultant al sistemului in raport cu acelasi punct O.
Axa centrala a unui sistem de vectori alunecatori.
|
|
unde s-au notat cu x,
y, z coordonatele punctului
, cu
proiectiile vectorului rezultant si
cu
proiectiile vectorului moment rezultant
al sistemului de vectori alunecatori pe axele sistemului de coordonate
considerat.
|
|
Locul geometric al punctelor pentru care torsorul de reducere al unui sistem de vectori alunecatori este minimal (modulul momentului rezultant minim) se numeste axa centrala a sistemului de vectori alunecatori.
|
Reducerea sistemelor de vectori alunecatori. Cazurile de reducere.
Cazul 1)
Cazul 2)
Cazul 3)
Cazul 4)
Cazul 4a)
Cazul 4b)
Considerand vectorul
Reducerea sistemelor de vectori concurenti Se considera ca vectorii sistemului sunt
concurenti in punctul O, deci O apartine suportului lui
Sistemul se incadreaza in cazul 1) de reducere, daca vectorul rezultant al sistemului este si el nul si deci sistemul este echivalent cu zero, sau in cazul 3), cand vectorul rezultant este nenul, cand se reduce la un vector unic, trecand prin O. Reducerea sistemelor de vectori coplanari
3) Daca
Reducerea sistemelor de vectori paraleli
Vectorul moment
rezultant este perpendicular pe directia lui
In aceste conditii, exista trei cazuri de reducere: -
-
-
Acesta trece sau
nu prin O, dupa cum
Punctul fix prin care trece suportul rezultantei unui sistem dat de forte paralele, cand directia lor comuna variaza, iar modulele raman aceleasi, se numeste centrul vectorilor paraleli. Centre de masa (centre de greutate) Asupra tuturor punctelor care alcatuiesc un corp de pe Pamant actioneaza forta gravitationala. Pentru un sistem de puncte materiale de mase mi, greutatile acestora, pot fi considerate ca fiind forte paralele.
se numeste centrul de masa (de greutate) al sistemului de puncte material (Pi). Proprietatile centrelor de masa Proprietatea 1: centrul de masa al unui sistem de puncte materiale se gaseste in interiorul oricarei suprafete convexe , care contine in interiorul sau toate punctele sistemului. Proprietatea 2: daca punctele materiale ale unui sistem se afla pe o dreapta, atunci centrul de masa se afla si el pe respectiva dreapta. Proprietatea 3: daca sistemul de puncte materiale se afla intr-un plan, atunci centrul de masa al sistemului se afla in acelasi plan. Proprietatea 4: daca un sistem de puncte materiale are un plan, o axa de simetrie sau un centru de simetrie, atunci centrul de masa al sistemului se afla in acel plan, pe acea axa respectiv in acel centru de simetrie.
Momente statice. Teorema momentelor statice Se numeste moment static al unui sistem de puncte materiale in raport cu un plan marimea scalara egala cu suma produselor dintre masele punctelor materiale si cotele acestora fata de planul considerat. Teorema momentelor statice: momentul static al unui sistem de puncte materiale in raport cu un plan este egal cu produsul dintre masa intregului sistem si cota centrului de masa al sistemului fata de respectivul plan.
Teoremele lui Guldin-Pappus Teorema 1: aria suprafetei generate de un arc de curba plana care se roteste in jurul unei axe din planul curbei (arcul fiind situat in intregime de aceeasi parte a axei) este egala cu lungimea arcului de curba, inmultita cu lungimea cercului descris de centrul de masa al curbei date, considerata omogena. Teorema volumul corpului generat prin rotirea unei suprafete plane inchise in jurul unei axe din planul sau (suprafata fiind omogena si situata in intregime de aceeasi parte a axei), este egal cu produsul dintre aria acestei suprafete si lungimea cercului descris de centrul ei de masa. Momente de inertie mecanice Se numeste moment de inertie mecanic al sistemului de puncte materiale in raport cu un plan suma produselor dintre masele punctelor sistemului si patratele distantelor acestora la plan. Daca planul se inlocuieste cu o axa sau cu un punct, se obtin momente de inertie axiale respectiv polare
Planare: Axiale:
Polare: Proprietati ale momentelor de inertie Momentele de inertie nu sunt independente. 2) Momentele de inertie sunt pozitive. 3) Daca punctele materiale se gasesc intr-un plan, atunci momentul de inertie fata de respectivul plan este nul. De asemenea, daca punctele se gasesc pe o axa, momentul de inertie fata de aceasta axa este nul. 4) Spre deosebire de momentele de inertie, momentele centrifugale pot fi pozitive, negative sau nule.
Momentul de inertie axial este egal cu suma momentelor de inertie in raport cu doua plane care se intersecteaza rectangular dupa acea axa.
|
Raza de inertie (raza de giratie).
Se numeste raza de inertie
(raza de giratie) distanta fata de un punct
(axa sau plan) a punctului in care, daca s-ar concentra toata
masa sistemului, s-ar obtine acelasi moment de inertie.
Momente de inertie in plan.
Pentru sistemele de puncte materiale situate intr-un
plan, fata de sistemul de coordonate carteziene Oxy, se pot
calcula trei momente de inertie si un moment centrifugal
Variatia momentelor de inertie in raport cu axe paralele
Momentul de inertie in raport cu o axa , paralela cu axa , care trece prin centrul de masa C al sistemului de puncte materiale, este egal cu suma dintre momentul de inertie in raport cu axa ce trece prin centrul de masa si produsul dintre masa M a sistemului cu patratul distantei d dintre cele doua axe (teorema axelor paralele sau teorema lui Steiner),
Variatia momentelor centrifugale fata de axe paralele
Se considera un sistem de axe O1x1y1z1, paralel cu sistemul Oxyz, cu originea in punctul O1 (a,b,c)
Daca O=C
Variatia momentului de inertie fata de axe concurente
Fata de
o axa

In cazul sistemului de puncte materiale situate intr-un plan, raportat la sistemul de coordonate carteziene Oxy
Directii principale de inertie. Momente principale de inertie.

Echilibrul punctului material liber supus actiunii unui sistem de forte.

Probleme care apar in statica punctului material liber:
a) probleme in care se dau fortele care actioneaza asupra punctului si se cer conditiile de echilibru;
b) probleme in care se da pozitia de echilibru a punctului si se cere determinarea uneia sau mai multor forte care, impreuna cu fortele date in problema, sa permita mentinerea in echilibru a punctului, in pozitia data;
c) probleme mixte, in care se dau o parte dintre parametri care definesc pozitia de echilibru si o parte dintre forte si trebuie determinati ceilalti parametri si restul de forte.
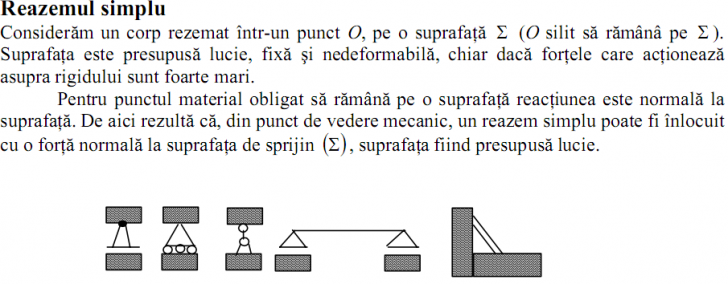
Statica punctului material supus la legaturi.
Punct material supus la legaturi, care este un punct material supus unei legaturi mecanice. Punctul material care se reazema pe o curba, pe o suprafata sau este obligat sa ramana intr-un punct fix in spatiu.


Statica solidului rigid supus la legaturi fara frecare.
Ecuatiile de echilibru ale solidului rigid
Se considera un solid rigid,
asupra caruia actioneaza un sistem de forte, S
, un sistem cartezian de axe de coordonate Oxyz, cu axe de versori
.
Un solid rigid se gaseste in echilibru daca sistemul de forte care actioneaza asupra sa este in echilibru.
,
pentru orice O punct din spatiu.
Teorema
|
|
Conditia necesara si suficienta ca un solid rigid, aflat sub actiunea unui sistem de forte, sa fie in echilibru este ca torsorul sistemului de forte, in raport cu un punct arbitrar din spatiu, sa fie nul
Legea echilibrului rezulta din principiul actiunii fortei.
|
|


Conditiile de echilibru ale unui sistem de forte care actioneaza asupra unui sistem de corpuri.
Conditii de echilibru pentru un sistem de corpuri
Sistemul de corpuri, actionat de un sistem de forte, este in echilibru daca, izoland fiecare subsistem (in particular, fiecare corp), acesta este actionat de sisteme de forte in echilibru.
|
|
Se
considera corpurile A1,A2, . ,An,
sistemele de forte exterioare care actioneaza asupra corpului Ai, de rezultante
si
, fortele interioare, i, j
(ca mai sus,
este forta
cu care corpul Aj actioneaza
asupra corpului Ai).
Teorema solidificarii
Sistemul de corpuri, pentru care torsorul fortelor interioare este nul, poate fi considerat ca un singur corp asupra caruia actioneaza fortele exterioare efectiv aplicate sistemului si fortele exterioare de legatura.Un sistem de corpuri poate fi si un sistem deformabil. Din principiul de mai sus nu rezulta ca rezultatele de la solidul rigid sunt aplicabile si mediilor deformabile (fluide, medii elastice).
Observatie:Spre deosebire de solidul rigid, pentru care conditiile sunt conditii necesare si suficiente de echilibru, pentru un sistem oarecare de corpuri, ele reprezinta numai conditii necesare nu si suficiente de echilibru. Conditiile sunt si suficiente, in cazul sistemelor nedeformabile (torsorul fortelor interioare nul).
38. Teorema echilibrului partilor
Daca intr-un sistem de puncte materiale sau de corpuri, actionat de un sistem de solicitari (forte si momente) in echilibru si supus unor legaturi mecanice, se izoleaza un subsistem, acesta este in echilibru sub actiunea fortelor ce actioneaza asupra lui (forte active si forte de legatura exterioare si interioare, datorate legaturilor cu restul de subsisteme din sistem).
ObservatieMetoda echilibrului partilor conduce la un sistem cu foarte multe ecuatii. In multe cazuri, intereseaza numai parametrii care definesc conditia de echilibru a sistemului de corpuri. Se determina, mai intai, acesti parametri si apoi fortele de legatura.
39&40.


Viteza unui punct material
Se numeste vector-viteza, sau, pe scurt viteza a punctului M marimea vectoriala definita prin derivata vectorului de pozitie in raport cu timpul:
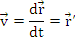
S-a folosit notatia
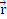 pentru derivata vectorului in raport cu timpul.
Miscarea unui punct material in care modulul vitezei este
constant se numeste miscare
uniforma.
pentru derivata vectorului in raport cu timpul.
Miscarea unui punct material in care modulul vitezei este
constant se numeste miscare
uniforma.
Miscarea unui punct material in care modulul vitezei variaza liniar cu timpul se numeste miscare uniform variata.
Acceleratia unui punct material.
Se numeste acceleratie a punctului material M marimea vectoriala definita prin derivata vitezei in raport cu timpul:
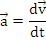
Viteza si acceleratia areolara
Se numeste viteza medie areolara marimea definita prin:
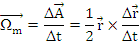
Daca Δt→0 se obtine viteza areolara instantanee marimea orientata a ariei elementare maturate de vectorul de pozitie raportata la timpul elementar in care aceasta a fost parcursa:
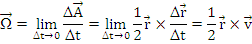
Componentele vitezei areolare sunt date de formulele:
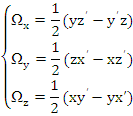
Componentele vitezei si acceleratiei in coordonate polare
Pentru miscarile plane, se pot utiliza coordonatele polare, raza polarasi respectiv unghiul polar.
r =r(t) θ=θ(t)
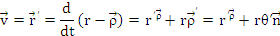
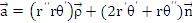
Componentele vitezei si acceleratiei in coordonate naturale ( intrinseci).
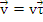
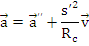
Cele doua proiectii se numesc: cea indreptata de-a lungul tangentei -acceleratie tangentiala, iar cea de-a lungul normalei principale -acceleratie normala
Componentele vitezei si acceleratiei in coordonate carteziene
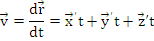
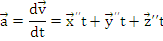
Miscari rectilinii ale punctului material
Miscarea rectilinie uniforma este o miscare a carei traiectorie este un segment de dreaptasi cu viteza de modul constant. Alegem sistemul cartezian de axe de coordonate Oxyz astfel incat axa Ox sa fie pe dreapta pe care are loc miscarea. La momentul initial t=0 al miscarii presupunem ca punctul material se afla in pozitia data de x = x si are viteza v = v .
x = x t + v , y = z = 0, ecuatiile miscarii rectilinii si uniforme. Daca o miscare are acceleratia nula, atunci miscarea este rectilinie si uniforma.
Miscarea rectilinie uniform variata
Miscarea cu traiectoria rectilinie si modulul acceleratiei constant este miscarea rectilinie uniform variata. Legea de miscare si viteza sunt date de formulele:
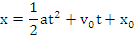
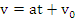
Exista relatia:
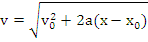
Miscarea circulara a punctului material
Miscarea circulara este miscarea a carei traiectorie este un cerc sau un arc de cerc. Se numeste viteza unghiulara marimea scalara egala cu derivata in raport cu timpul a unghiului descris de raza solidara cu punctul care se misca:
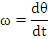
Se numeste acceleratie unghiulara marimea scalara care caracterizeaza variatia vitezei unghiulare in unitatea de timp si se exprima prin derivata vitezei unghiulare in raport cu timpul:
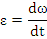
Miscarea circulara uniform variata este miscarea circulara, pentru care a = const . Rezulta
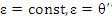
ceea ce conduce, prin integrare, la
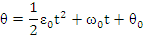
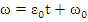
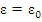
unde θ,ω ,ε sunt valorile functiilor corespunzatoare la momentul initial al miscarii.
Distributia vitezelor in cazul solidului rigid
|
|
Vectorul
reprezinta
viteza punctului O si se noteaza cu
.
|
|
|
|
|
|
expresia matematica a teoremei lui Euler pentru distributia de viteze intr-un solid rigid.
Pe componente, relatia se scrie
|
|
unde s-au notat cu
cele trei
componente ale vectorului
.
Distributia acceleratiilor in cazul solidului rigid
,
).
,
acceleratia originii sistemului mobil si cu
.
Se obtine expresia teoremei lui Euler pentru distributia acceleratiilor intr-un solid rigid
|
|
In cazul general, poate exista un punct care are acceleratia nula . Daca exista, acest punct se numeste polul acceleratiilor.
Miscarea de translatie
Un solid rigid efectueaza o miscare de translatie daca o dreapta oarecare a rigidului ramane, in tot timpul miscarii, paralela cu ea insasi. Traiectoriile pe care le descriu punctele solidului pot fi curbe oarecare.
Dupa forma traiectoriei, tipurile de translatii mai des intalnite in practica sunt:
- rectilinii - miscarea sertarului unui birou, miscarea ascensorului, miscarea unui piston intr-un cilindru;
- circulare - miscarea bielei de cuplare a doua roti, caz in care punctele bielei descriu arce de cicloida, miscarea unui leagan etc;
- alte translatii - biela de cuplare a rotilor unei locomotive etc.
.
|
|
Pentru orice punct al solidului, are loc relatia
|
|
|
|
Toate punctele unui solid rigid, aflat in miscare de translatie, au aceeasi viteza si aceeasi acceleratie.
Solidul rigid in miscare de translatie are trei grade de libertate.
Miscarea de rotatie
Un solid rigid se afla in miscare de rotatie daca cel doua puncte distincte ale sale raman fixe in spatiu in tot timpul miscarii.
Daca O si O' sunt punctele fixe, atunci
orice
ramane
fix, deci OO' este o axa fixa
si se numeste axa de rotatie. Din acest motiv,
miscarea de rotatie se numeste si miscarea solidului
cu o axa fixa.
In
studiul miscarii de rotatie, este esential unghiul
, a carui masura, in radiani, este
Miscarea este perfect
determinata daca se cunoaste marimea acestui unghi ca
functie de timp
. Solidul rigid in miscare de rotatie are un singur grad de libertate.
.
|
|
|
|
|
|
|
|
|
|
Teorema 1
In miscarea de rotatie a unui solid rigid in jurul unei axe fixe, in orice moment, toate punctele solidului au aceeasi viteza unghiulara si aceeasi acceleratie unghiulara.
Miscarea elicoidala
Miscarea unui solid rigid se numeste miscare elicoidala daca o dreapta solidara cu solidul isi pastreaza in tot timpul miscarii suportul fix. Dreapta se numeste axa miscarii elicoidale.
|
|
unde
este cota
originii sistemului mobil, fata de sistemul fix, si
este unghiul
dintre axele Ox si O1x1.
Solidul rigid aflat in miscare elicoidala are doua grade de libertate.
Miscarea plan-paralela
Miscarea unui solid rigid se numeste miscare plan-paralela daca exista cel putin trei puncte necoliniare ale sale care sunt continute intr-un plan fix din spatiu, in tot timpul miscarii.
In cazul in care solidul are forma unei placi plane, de grosime neglijabila si miscarea acestuia are loc in propriul sau plan, miscarea se numeste miscare plana.
Solidul rigid aflat in miscare plan-paralela are trei grade de libertate.
Miscarea solidului rigid cu un punct fix
.
,
Unghiurile lui Euler
- unghiul de precesie
, care este unghiul
si se
afla in planul (
);
- unghiul de rotatie proprie
, unghiul NOx, care se afla in planul (Oxy);
- unghiul de nutatie
, unghiul
, care se afla in planul
. Masurile unghiurilor
si
sunt, de
asemenea, functii de timp, iar ON este axa (linia) nodurilor
, intersectia planelor (Oxy) si (
).
Aceste trei unghiuri sunt independente. Ele se folosesc, alaturi de coordonatele originii sistemului de coordonate mobil, pentru caracterizarea miscarii sau pozitiei de repaus a unui solid rigid. Cele trei unghiuri se numesc unghiurile lui Euler.
Notiuni fundamentale ale dinamicii punctului material (impuls, lucru mecanic, moment cinetic, energie cinetica, energie potentiala, energie mecanica)
Marimea vectoriala care caracterizeaza miscarea mecanica a unui punct in ce priveste capacitatea ei de a se transmite unui sistem material tot sub forma de miscare mecanica, marime care se exprima prin produsul dintre masasi viteza punctului material, se numeste impulsul punctului material.
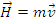
Se numeste momentul cinetic al unui punct material fata de un pol momentul impulsului punctului material fata de punctul considerat.
Daca se noteaza cu O punctul fata de care se calculeaza momentul cinetic, atunci:
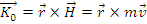
unde
 este
vectorul de pozitie al punctului material fata de O, m-masa
punctului material,
este
vectorul de pozitie al punctului material fata de O, m-masa
punctului material,
iar
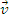 -viteza
acestuia.
-viteza
acestuia.
Se
numeste lucrul mecanic elementar
al fortei
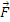 produsul
scalar dintre forta
produsul
scalar dintre forta
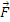 si
variatia infinitezimala d
si
variatia infinitezimala d
 a
vectorului de pozitie al punctului material:
a
vectorului de pozitie al punctului material:
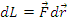
Se numeste lucrul mecanic al unei forte integrala curbilinie a lucrului mecanic elementar pe arcul descris de punctul de aplicatie al fortei.
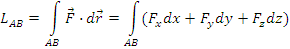
O
forta
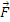 se
numeste forta
conservativa daca exista U(x,y,z)
- functie scalara de coordonate- astfel incat:
se
numeste forta
conservativa daca exista U(x,y,z)
- functie scalara de coordonate- astfel incat:
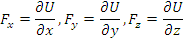
Functia scalara de coordonatele unui punct, al carei gradient este egal cu forta care actioneaza asupra acestui punct, se numeste functie de forta. In cazul fortelor conservative,
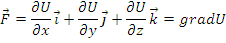
Marimea scalara ce care se exprima prin raportul dintre lucrul mecanic elementar si timpul elementar corespunzator se numeste putere. Marimea scalara ce caracterizeaza capacitatea de transformare a miscarii mecanice a unui punct material in lucru nemecanic se numeste energie cinetica a punctului material. Ea se exprima prin jumatatea produsului dintre masa si patratul vitezei punctului:
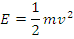
Marimea care caracterizeaza capacitatea miscarii nemecanice de a trece intr-o anumita cantitate de miscare mecanica se numeste energie potentiala. Marimea care caracterizeaza capacitatea miscarii nemecanice de a trece intr-o anumita cantitate de miscare mecanica se numeste energie potentiala. Suma dintre energia cineticasi energia potentiala a punctului material se numeste energie mecanica.
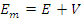
Teorema impulsului punctului material
Derivata in raport cu timpul a impulsului unui punct material este egala cu rezultanta F a fortelor care actioneaza asupra acestui punct:
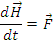
Teorema momentului cinetic pentru punctul material
Derivata in raport cu timpul a momentului cinetic al unui punct material, calculat fata de un pol O, este egala cu momentul rezultantei F al fortelor care actioneaza asupra punctului material, moment calculat in raport cu acelasi pol O.
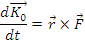
Teoreme de conservare
Din teorema impulsului punctului material, daca F=0, rezulta:
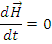
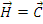
Pornind acum de la teorema momentului
cinetic, va rezulta ca acesta se conserva daca momentul fortei
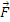 , in
raport cu un punct fix O, este nul.
, in
raport cu un punct fix O, este nul.
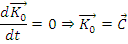
unde
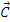 este un
vector constant.
este un
vector constant.
Teorema
In cazul in
care rezultanta
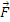 a fortelor care actioneaza asupra
punctului material deriva dintr-o functie de forta, energia
mecanica a punctului material se conserva.
a fortelor care actioneaza asupra
punctului material deriva dintr-o functie de forta, energia
mecanica a punctului material se conserva.
Daca in punctul A(x0,y0,z,o), U=0 si B(x,y,z) este un punct oarecare:
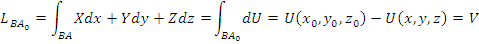
Teorema energiei cinetice si a lucrului mecanic pentru punctul material
Variatia energiei cinetice a unui
punct material este egala cu lucrul mecanic
elementar al rezultantei
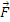 a
fortelor care actioneaza asupra punctului material:
a
fortelor care actioneaza asupra punctului material:
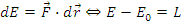
Ecuatiile diferentiale ale miscarii in diferite sisteme de coordinate
In coordonate cilindrice, ecuatia fundamentala a dinamicii se scrie:
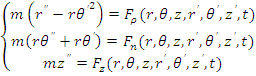
iar in coordonate intrinseci:
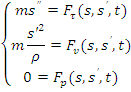
Miscarea unui punct material greu in vid
Un exemplu deosebit de important de miscare a unui punct
material liber il constituie miscarea punctului material sub
influenta greutatii proprii, cand se neglijeaza
rezistenta aerului, deci in vid. Pentru a studia aceasta miscare
se considera un punct material lansat intr-un
punct O de pe suprafata Pamantului, cu viteza
initiala
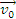 , a carei directie face unghiulα cu planul orizontal.
, a carei directie face unghiulα cu planul orizontal.
Se alege R =(
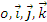 ), cu Oy pe directie verticala, Ox pe
orizontala in planul vertical care-l contine pe
), cu Oy pe directie verticala, Ox pe
orizontala in planul vertical care-l contine pe
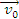 .
La un moment dat, punctul material ocupa
pozitia A si asupra sa
actioneaza doar forta de greutate
.
La un moment dat, punctul material ocupa
pozitia A si asupra sa
actioneaza doar forta de greutate
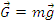 . Se obtine sistemul:
. Se obtine sistemul:
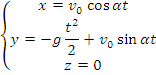
care, prin eliminarea lui t, duce la ecuatia traiectoriei :
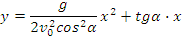
care este o parabola. Inaltimea maxima la care urca punctul material este:
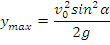
In cazul unghiului de 90 de grade, cele mai importante cazuri sunt: -miscarea ascendenta, cu viteza initiala orientata vertical in sus; -miscarea descendenta; -miscarea orizontala.
Miscarea unui punct material greu in aer
S-a stabilit ca rezistenta la inaintare, in cazul unui punct material greu in aer, depinde de vectorul viteza :
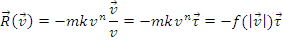
Sub influenta celor doua
forte, punctul material care este lansat din punctul O, sub un
unghi αfata de orizontalasi cu viteza
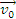 .
Ecuatia de miscare a punctului material este
data ecuatia fundamentala:
.
Ecuatia de miscare a punctului material este
data ecuatia fundamentala:
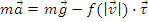
Se obtine sistemul de ecuatii diferentiale:
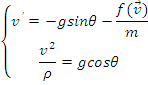
Miscarea unui punct material sub actiunea unei forte central
O forta se numeste forta centrala daca
suportul ei trece, in tot timpul miscarii, printr-un punct fix O,
numit centrul fortelor
. Exista un vector constant
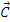 astfel
incat
astfel
incat
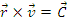
Traiectoria
unui punct material liber actionat de o forta centrala este o traiectorie plana, miscarea facandu-se
intr-un plan care contine centrul fortelor. Sub actiunea unei
forte centrale, un punct material liber se
misca cu viteza areolara
Ecuatia lui Binet
Pentru
studiul miscarii unui punct material sub influenta unei
forte centrale, s-a obtinut ecuatia lui Binet, care se scrie ca
o ecuatie diferentiala de ordinul al doilea, cu necunoscuta
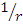 , de
variabila θ :
, de
variabila θ :
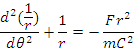
Miscarea punctului material in cazul particular al fortei atractiei universale.
Forta atractiei universale este un exemplu foarte important de forta centrala. Modulul acestei forte este
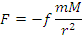
Se noteaza cu:
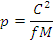
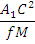
si se
obtine:
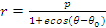
Sub actiunea unei forte de atractie universala, un punct material liber care se deplaseaza pe suprafata Pamantului descrie o conica. Din geometria analitica, se stie ca respectiva conica este: - o elipsa daca e < 1; - o parabola daca e = 1; - o hiperbola daca e > 1.
Notiuni fundamentale ale dinamicii sistemelor de puncte si a solidului rigid
Fiind dat un sistem de puncte materiale S=(Mi)1≤i≤n, de mase mi si viteze vi ,i =1,, n , se numeste impulsul sistemului S suma impulsurilor punctelor sistemului, adica:
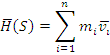
Se stabileste relatia
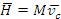
unde s-a notat cu
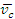 viteza centrului de masa al sistemului. Impulsul unui sistem de
puncte materiale este egal cu impulsul unui punct
material, avand masa egala cu masa intregului sistem, situata in
centrul sau de masa. Fiind dat un sistem de puncte materiale S=(Mi)1≤i≤n,
de mase mi si viteze vi ,i =1,, n ,
se numeste momentul cinetic al
sistemului S in raport cu un punct O suma momentelor
cinetice ale punctelor materiale din sistem in raport cu punctul considerat:
viteza centrului de masa al sistemului. Impulsul unui sistem de
puncte materiale este egal cu impulsul unui punct
material, avand masa egala cu masa intregului sistem, situata in
centrul sau de masa. Fiind dat un sistem de puncte materiale S=(Mi)1≤i≤n,
de mase mi si viteze vi ,i =1,, n ,
se numeste momentul cinetic al
sistemului S in raport cu un punct O suma momentelor
cinetice ale punctelor materiale din sistem in raport cu punctul considerat:
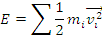
Expresii ale momentului cinetic si energiei cinetice ale sistemelor de puncte materiale si solidului rigid pentru miscari particulare.
Fiind dat un sistem de puncte materiale S=(Mi)
, de mase mi si viteze
, se numeste impulsul sistemului S suma
impulsurilor punctelor sistemului, adica
Observatie. In cazul solidului rigid, suma se transforma in integrala.
|
Ex. |
|
|
|
unde s-a notat cu
viteza centrului de masa al sistemului de
puncte materiale.
Propozitie
Impulsul unui id oa de puncte id oar este egal cu impulsul unui punct material, avand masa egala cu masa intregului id oa, situata in id oar de masa al sistemului.
Observatie
Impulsul sistemului de puncte id oar sau al solidului rigid nu depinde de miscarea punctelor id oar id oarve a solidului rigid, id oar de viteza centrului de masa.
Fiind dat un sistem de puncte materiale S=(Mi)
, de mase mi si viteze
, se numeste momentul cinetic al sistemului S in
raport cu un punct O suma momentelor cinetice ale punctelor materiale din
sistem in raport cu punctul considerat
|
|
Fiind dat un sistem de puncte materiale S=(Mi)
, de mase mi si viteze
, energia cinetica a sistemului de puncte este
suma energiilor cinetice ale punctelor materiale care alcatuiesc sistemul
S
|
|
Teorema impulsului pentru sisteme de puncte materiale si solid rigid
Derivata in raport cu timpul a impulsului unui sistem de puncte materiale este egala cu vectorul rezultant al fortelor exterioare, adica
Teorema centrului de masa
Centrul maselor unui sistem de puncte materiale are aceeasi miscare ca a unui punct material care are masa egala cu masa intregului sistem si asupra caruia actioneaza o forta egala cu vectorul rezultant al fortelor exterioare
Teoremele generale ale dinamicii sistemelor de puncte materiale in raport cu centrul de masa
Teorema impulsului
Derivata in raport cu timpul a impulsului unui sistem de puncte materiale este egala cu vectorul rezultant al fortelor exterioare, adica:
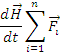
Teorema centrului de masa
Centrul maselor unui sistem de puncte materiale are aceeasi miscare ca a unui punct material care ar avea o masa egala cu masa intregului sistem si asupra caruia ar actiona
o forta egala cu vectorul rezultant al fortelor exterioare:
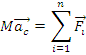
Teoremele momentului cinetic pentru sisteme de puncte materiale si solid rigid
Momentul cinetic
al unui sistem de puncte materiale in raport cu un punct fix O este egal cu
suma dintre momentul cinetic al centrului de masa, considerat ca un punct
material a carui masa este egala cu masa intregului sistem
si momentul cinetic
in
miscarea relativa a sistemului in raport cu centrul de masa.
Teorema 2 (teorema momentului cinetic sau teorema a doua a momentului impulsului)
Pentru un sistem de puncte materiale (solid rigid), derivata in raport cu timpul a momentului cinetic, calculat in raport cu un punct fix O, este egala cu vectorul moment rezultant al fortelor exterioare fata de acelasi punct fix O, adica
Teorema 3 (teorema momentului cinetic in raport cu centrul de masa)
Derivata in raport cu timpul a momentului cinetic al sistemului de puncte materiale in raport cu centrul de masa este egala cu vectorul moment rezultant al fortelor exterioare, calculat in raport cu centrul de masa.
Teoremele energiei cinetice si a lucrului mecanic pentru sisteme de puncte materiale si solid rigid.
Teorema 1
Energia cinetica a unui sistem de puncte materiale, calculata in raport cu un sistem de referinta fix, este egala cu suma dintre energia cinetica a centrului de masa, considerat ca un punct material a carui masa este egala cu masa intregului sistem si energia cinetica in miscarea relativa a sistemului in raport cu centrul de masa
Teorema 2 (teorema energiei cinetice si a lucrului mecanic)
In cazul unui sistem de puncte materiale (solid rigid), variatia energiei cinetice, calculata in raport cu un sistem de referinta fix, este egala cu suma dintre lucrul mecanic al fortelor exterioare si lucrul mecanic al fortelor interioare
Dinamica solidului cu o axa fixa
Se considera
un solid rigid de masa m, in
miscare de rotatie in jurul axei
, axa de
rotatie a miscarii.
|
|
|
|
|
|
,
|
|
|
|
|
Dinamica rigidului cu un punct fix
Asupra lui
actioneaza un sistem de forte
exterioare date:
|
|
|
|
format din trei ecuatii, cunoscute sub numele de ecuatiile lui Euler pentru rigidul cu un punct fix.
1) cazul Euler-Poinsot, cu conditiile Mx = 0 , My = 0 , Mz = 0.
2) cazul Lagrange-Poisson, pentru
si J1
= J2 .
3) cazul
, J1 = J2 = 2J3.
77. Derivata absoluta a unui vector
Se
considera un vector
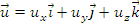
Se calculeaza derivata acestuia in raport cu sistemul de referinta fix.
Se introduce notatia:
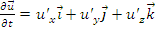
Pentru versorii
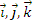 considerati invariabili.
considerati invariabili.
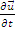 se numeste derivate
locala a vectorului
se numeste derivate
locala a vectorului
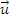
Se obtine:
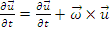
formula de calcul pentru derivata
absoluta (fata de sistemul de coordonate fix) a unui
vector variabil
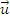 , dat
prin componentele sale pe axele mobile.
, dat
prin componentele sale pe axele mobile.
Compunerea vitezelor in miscarea relativa a unui punct material
Pentru miscarea relativa a unui punct material se stabilesc relatiile:
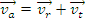
Unde
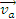 - viteza absoluta a
punctului P,
- viteza absoluta a
punctului P,
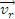 viteza relativa
(locala) a lui P,
viteza relativa
(locala) a lui P,
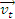 viteza
de transport a lui P.
viteza
de transport a lui P.
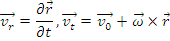
Viteza absoluta a unui punct material este egala cu suma vectoriala dintre viteza relativasi viteza de transport a punctului.
Compunerea acceleratiilor in miscarea relativa a unui punct material
Se numeste acceleratie complementara sau
acceleratia lui Coriolis,
notata cu
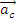 , vectorul egal cu
, vectorul egal cu
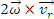 r .
Pentru miscarea relativa a unui punct material se stabilesc
relatiile:
r .
Pentru miscarea relativa a unui punct material se stabilesc
relatiile:
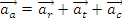
unde - acceleratia absoluta, notata cu
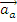 , acceleratia relativa
, acceleratia relativa
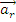 si acceleratia de transport at ,
adica :
si acceleratia de transport at ,
adica :
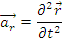
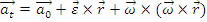
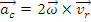
Relatia reprezinta relatia de compunere a acceleratiilor in miscarea relativasi se poate enunta sub forma: Acceleratia absoluta a unui punct material este egala cu suma vectoriala dintre acceleratia relativa, acceleratia de transport si acceleratia Coriolis.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |