Starea spatiala de tensiuni
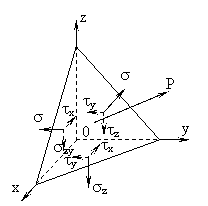
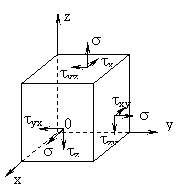
Daca dintr-un corp masiv, deformabil, solicitat de forte externe oarecare in echilibru, se izoleaza un element de volum de forma paralelipipedica, va trebui ca pe fetele paralelipipedului sa actioneze in general tensiuni normale si tangentiale, ca masura a actiunii partii de corp indepartata (8.a).
Acesta constituie cazul starii spatiale de tensiuni.
Ca si in cazul starii plane de tensiuni, tensiunile normale poarta un singur indice (indicele directiei proprii), iar tensiunile tangentiale cate doi indici (indicele directiei proprii si indicele normalei la planul in care actioneaza).
a) b)
Fig. 8
Scriind ecuatiile de echilibru pentru paralelipipedul detasat, prin suma de momente in raport cu axele sistemului de referinta se obtine legea dualitatii sau paritatii tensiunilor tangentiale,
txy tyx tyz tzy tzx txz
Tinand seama de legea dualitatii, din cele noua componente ale tensiunilor actionand pe trei plane perpendiculare ce se pot duce printr-un punct oarecare, numai sase sunt independente.
Cele noua componente ale tensiunilor, definind starea de tensiuni intr-un punct al unui corp solicitat spatial, constituie tensorul tensiunilor si se noteaza simbolic prin tabloul,
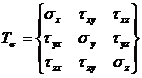 , (19)
, (19)
in care elementele unei linii sunt constituite din tensiunile orientate dupa aceeasi directie, iar elementele unei coloane, din tensiunile actionand in acelasi plan. Tensorul tensiunilor unitare este simetric fata de diagonala principala in baza legii dualitatii.
Cu ajutorul unui plan inclinat se detaseaza din elementul considerat un tetraedru ca in fig. 8.b. Tensiunile de pe fata inclinata a tetraedrului pot fi determinate in functie de tensiunile paralele cu axele sistemului si de pozitia planului inclinat. Pentru aceasta se noteaza cu dA aria sectiuni inclinate si cu l, m si n cosinii directori ai normalei acestei sectiuni. Tensiunea necunoscuta pe sectiunea inclinata se noteaza cu p si are componentele pe axele de referinta px, py, pz.
Scriind ecuatiile de echilibru prin proiectii pe directia axelor va rezulta, pxdA - xldA - txy mdA - txz ndA = 0
pydA - ymdA - tyx ldA - tyz ndA = 0
pzdA - z ndA - tzx ldA - tzy mdA = 0
de unde,
px = l x + mtxy + ntxz
py = ltyx + m y + ntyz (20)
pz = ltzx + mtzy + n z
Tensiunea de pe suprafata oblica va fi,
![]() (21)
(21)
iar componenta dupa normala,
σ = lpx + mpy + npz = l2 x + m2 y + n2 z + 2lmtxy + 2lntxz
+2mntyz (22)
Tensiunea tangentiala pe sectiunea oblica va fi,
![]() (23)
(23)
Asemanator cu starea plana de tensiuni, si pentru starea spatiala, exista trei plane perpendiculare duse prin punctul respectiv, in care tensiunile tangentiale sunt nule iar tensiunile normale au valori extreme. Normalele la cele trei plane definesc directiile principale de solicitare. Tensiunile normale , dirijate dupa aceste directii se numesc tensiuni principale. Tensorul starii spatiale de tensiuni se poate exprima in functie de tensiunile normale principale avand forma,
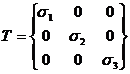 (24)
(24)
Daca > > este tensiunea normala maxima, tensiunea minima iar tensiunea mini-max.
Tensiunile principale se pot determina cu ajutorul relatiilor (20). Pentru aceasta se admite ca sectiunea oblica este unul din planele principale,
adica tensiunile tangentiale lipsesc, iar tensiunea totala este orientata dupa normala, adica coincide cu = p).
Atunci,
px = l ; py = m ; pz = n
Introducand in (20) rezulta,
l( x ) + mtxy + ntxz
ltyx + m( y ) + ntyz (25)
ltzy + mtzx + n( z
Sistemul (25) admite solutii diferite de zero numai daca determinantul sau este nul:
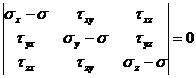
Din dezvoltarea determinantului rezulta ecuatia de gradul trei in
- I1 + I2 - I3 = 0 (26)
in care I1, I2 si I3 sunt invariantii starii de tensiuni:
I1 = x y z
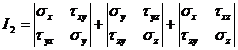 (27)
(27)
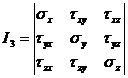
Ecuatia (26) are trei solutii reale care sunt tensiuni normale principale
Introducand aceste solutii in sistemul (25) si tinand seama ca,
l2 + m2 + n2 = 1 (28)
vor rezulta directiile principale de solicitare.
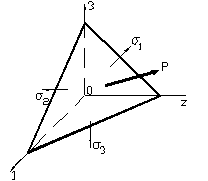
Fig. 9
Pentru calculul tensiunilor tangentiale maxime precum si a directiilor acestora, se considera starea spatiala de tensiuni ca fiind determinata prin tensiunile normale principale si directiile acestora (figura.9).
In acest caz tensiunea totala p este,
![]() (29)
(29)
iar tensiunea tangentiala,
![]()
Rezulta in urma gruparilor,
![]() (30)
(30)
Tinand seama de relatia (28), relatia (30) poate fi scrisa sub forma:
τ2 = l2m2(σ1-σ2)2 + m2(1-l2-m2) (σ2-σ3)2 + l2(1-l2-m2)(σ3-σ1)2
Se anuleaza derivatele partiale ale expresiei obtinute in raport cu l si m si se obtin relatiile:
![]()
![]()
In urma unor transformari simple relatiile obtinute ajung la forma:
l=0
m=0 (31)
Solutia l = m = 0 trebuie eliminata caci ea corespunde directiei axei Oz. De asemeni nu se poate admite l≠0 n≠0, caci in acest caz ar fi posibila simplificarea ecuatiilor (31) prin l si m, si apoi prin scaderea relatiilor ar ramane σ1= σ2, ceea ce nu este adevarat. Raman astfel urmatoarele posibilitati:
- l ≠ 0; m = 0, rezultand din ecuatia prima,
![]() ; m=0 ;
; m=0 ; ![]() (32)
(32)
- l = 0; m ≠ 0,rezultand din ecuatia a doua,
l = 0 ; ![]() ;
; ![]() (33)
(33)
Derivand in mod asemanator in raport cu m se obtine inca o solutie :
![]() ;
; ![]() ; n=0 (34)
; n=0 (34)
Relatiile (32), (33) si (34) arata ca valorile extreme ale tensiunilor tangentiale apar in plane paralele cu una din directiile principale si facand unghiuri de 45o cu celelalte doua directii principale.
Inlocuind in relatia (30) expresiile obtinute pentru cosinii directori l, m si n rezulta valorile extreme ale tensiunilor tangentiale:
![]() ;
; ![]() ;
; ![]() (35)
(35)
Tensiunea tangentiala maxima corespunde diferentei celei mai mari dintre tensiunile normale principale. Astfel daca σ1>σ2> σ3
![]()
In mod asemanator cu starea plana de tensiuni si starea spatiala poate fi reprezentanta grafic intr-un sistem de axe σOτ. Pentru aceasta se examineaza tensiunile σ si τ in plane paralele cu tensiunile principale.
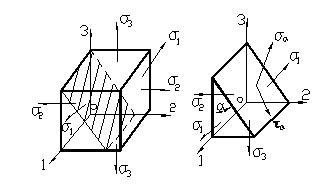
Fig. 10
In fig.10 s-a sectionat elementul printr-un astfel de plan. Notand cu dA aria fetii inclinate a tetraedului detasat, din ecuatiile de echilibru va rezulta:
σ·dA - σ2·dA·cosα·cosα + σ3·dA·sinα·sinα =0
τ ·dA - σ2·dA·cosα·sinα + σ3·dA·sinα·cosα =0
sau, σα=σ2·cos2α+σ3·sin2α
τα=(σ2- σ3)sinα ·cosα
Introducand unghiul dublu se obtine:
![]() (36)
(36)
![]()
Eliminand unghiul 2α intre relatiile (36) va rezulta:
![]() (37)
(37)
adica ecuatia unui cerc in coordonate σα si τα . Acesta este cercul lui Mohr pentru variatia tensiunilor σ si τ in plane paralele cu tensiunea principala σ1. In
mod asemanator se gasesc si ecuatiile cercurilor pentru tensiunile din planele paralele cu celelalte doua tensiuni principale.

Fig. 11
In fig.11 au fost duse toate cele trei cercuri Mohr. Tensiunile σ si τ din planele ce nu sunt paralele cu niciuna dintre tensiunile principale sunt date de punctele aflate in domeniul hasurat (punctele P).
In plane
egal inclinate fata de cele trei directii principale, denumite
plane octaedrice, tensiunile σ si τ poarta
numele de tensiuni octaedrice. Cosinii directori ai planelor octaedrice vor fi:
l=m=n=![]() iar din (29) va
rezulta:
iar din (29) va
rezulta:
![]() (38)
(38)
Cu ajutorul relatiei (22) se obtine tensiunea normala ocatedrica :
![]() (39)
(39)
ca medie a tensiunilor normale principale.
Tensiunea tangentiala octaedrica va fi :
![]() (40)
(40)
sau , ![]()
![]() (41)
(41)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |