
Caracteristicile unui spectru
In aplicatiile spectroscopiei radiatiei gama, detectorii produc la iesire un puls al carui marime este proportionala cu energia cedata de fotonii incidenti mediului detector. Sistemul de masurare trebuie sa sorteze toate pulsurile generate si sa afiseze numarul lor relativ. Aceasta sarcina este efectuata de analizorul multicanal si rezultatul final al analizei consta intr-o histograma (spectru) a pulsurilor detectate la iesire, aranjate in functie de marime. Un spectru de amplitudine al impulsurilor reprezinta o reprezentare directa a spectrului energetic al radiatiei gama care interactioneaza cu mediul detector si constituie informatia spectroscopica utilizata in analiza nedistructiva cu radiatii gama.
1. Raspunsul caracteristic al unui detector
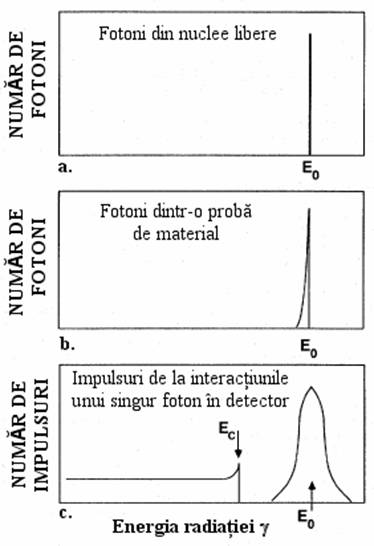
Fara a tine cont de tipul detectorului utilizat, spectrele masurate au multe caracteristici in comun. Sa consideram spectrul unei surse de radiatii gama monoenergetica, de energie E0, produs in urma dezintegrarii unui nucleu (fig. 5 a.). Fotonii
|
Fig. 5. Spectru fotonic ideal: a. produs de nuclee libere, b. emis de o proba de material si c. produs in urma interactiilor din mediul detector. |
radiatiei gama care iau nastere in urma tranzitiilor nucleare, presupun schimbari energetice specifice, care prezinta mici fluctuatii ale valorilor datorate a doua efecte: incertitudinea energetica a fotonului transmis (incertitudine Heisenberg) si efectele de recul la emisia fotonilor radiatiei gama. Aceste incertitudini sunt finite, dar neglijabile in comparatie cu alte efecte de extindere energetica si din aceste considerente nu sunt indicate in figura.
Deoarece fotonii radiatiei gama detectate, nu provin de obicei din nuclee libere, ci sunt emise din mediu material, unii dintre ei sufera imprastieri inainte de parasirea probei radioactive. Aceste imprastieri afecteaza fotonii cu energii mai mici ca E0, iar spectrul energetic al fotonilor emisi de o proba de material se extinde usor la energii mai mici ca E0 (fig. 5b.). Marimea extinderii este destul de mica, comparativ cu cea produsa de alte efecte, iar in figura este exagerata pentru a atrage atentia asupra existentei ei. Trebuie remarcat faptul ca unele radiatii gama, dupa parasirea probei, por suferii imprastieri in mediul exterior inainte de patrunderea in detector, iar acest efect este regasit in spectrul energetic final.
Cand radiatia gama patrunde in materialul detector ea transfera o parte sau toata energia sa unui electron atomic, eliberandu-l de legaturile atomice. Acest electron liber transfera energia sa cinetica, in urma unor ciocniri succesive, altor electroni atomici din mediul detector.
Cantitatea de energie necesara producerii perechilor electron-ion in mediul detector determina cantitatea de sarcina care va fi produsa intr-un proces de detectie, implicand o cantitate data de energie cedata. O interactiune fotoelectrica transfera toata energia fotonului incident unui fotoelectron. Acest electron cauzeaza, ulterior, ionizari multiple pana cand energia sa este diminuata. Cantitatea de sarcina produsa in acest tip de eveniment este, deci, proportionala cu energia fotonului incident.
In urma unei interactiuni prin imprastiere Compton se transfera numai o parte din energia fotonului incident unui electron, iar acest electron poate produce ionizari succesive pana cand energia sa este diminuata. Cantitatea de sarcina produsa in acest tip de eveniment este nu este proportionala cu energia fotonului incident si nu ofera informatii despre acest foton. Multiplele imprastieri Compton ale aceluias foton pot produce o cantitate de sarcina apropiata de valoarea reprezentata de intreaga energie a fotonului initial. Semnalul produs Compton, in general reprezentand o singura interactie de imprastiere, este de marime mai mica decat semnalul obtinut de la intreaga energie a fotonului. Raspunsul ideal al detectorului la interactiunea fotoelectrica si Compton este reprezentat in figura 5c. Energia maxima care poate fi cedata mediului detector printr-o imprastiere Compton provine de la evenimentul in urma caruia fotonul este imprastiat la 1800. Pulsurile generate Compton in detector sunt distribuite sub acest maxim energetic (Ec in fig. 5c.) si constituie o sursa pentru pulsurile din "fond" fara a furniza informatii energetice folositoare.
Picul de energia totala (fig. 5c.) este largit semnificativ de fluctuatia statistica in numar a perechilor electron-ion produse de fotoelectron. Acest efect este principalul furnizor la largimea picului de energie totala si din acest considerent este un factor dominant in rezolutia energetica a detectorului.
2. Caracteristicile unui spectru
O reprezentare mult mai realista a unui spectru generat intr-un detector de un flux de radiatii gama monoenergetica este indicata in figura 6. Zonele distinctive ale unui spectru sunt notate de la A la G.
|
|
Fig. 6. Reprezentare reala a unui spectru produs de o sursa gama monoenergetica.
Analiza zonelor spectrale:
A. Fotopicul de energie totala. Acest pic reprezinta impulsurile care provin de la interactiile fotoelectrice cu cedare totala a energiei in mediul detector. Unele impulsuri pot proveni de la interactiuni Compton singulare sau multiple urmate de interactiune fotoelectrica. Picul central (centroidul) reprezinta energia fotonului E0. Aria neta, situata deasupra fondului, reprezinta numarul total al interactiunilor cu cedare integrala a energiei in detector si este de obicei proportional cu masa izotopului care emite radiatia.
B. Fondul continuu Compton. Aceste pulsuri, distribuite usor pana la energia maxima Ec, provin in urma interactiunilor care implica o pierdere partiala a energiei in mediul detector. Evenimentele Compton sunt principalele surse de impulsuri in acest fond situat sub picul de energie totala in spectrele mai complexe.
C. Marginea Compton. Reprezinta energia maxima pierduta de fotonul incident printr-o imprastiere Compton. Este largita asimetric fata de picul corespunzator energiei maxime (Ec) pe care fotonul radiatiei gama de energie E0 poate sa o transfere unui electron liber intr-o singura ciocnire. Aceasta corespunde unei coliziuni centrale dintre un foton si un electron, dupa care electronul se deplaseaza inainte, iar fotonul este imprastiat inapoi la 1800.
D. "Valea" Compton. Pentru o sursa monoenergetica, pulsurile din aceasta zona apar fie evenimentelor de imprastiere Compton multiple fie de la interactiunile de energie totala ale fotonilor care au suferit imprastieri la unghiuri mici (in materialul sursei sau in alte materiale) inainte de intrarea in detector. Fotonii neimprastiati de la o sursa monoenergetica nu pot produce pulsuri in aceasta regiune in urma unei singure interactii in detector. In spectre complexe aceasta regiune poate contine pulsuri generate Compton de fotoni cu energii inalte.
E. Picul de retroimprastiere. Acest pic este cauzat de radiatiile gama care au interactionat prin imprastiere Compton intr-unul din materialele care inconjoara detectorul. Radiatiile gama imprastiate la mai mult de 1100 - 1200 vor iesi cu energii apropiate in domeniul 200 - 250 keV. Deci, o sursa monoenergetica va crea multe radiatii gama imprastiate a caror energie va fi in jurul acestei valori minime.
F. Regiunea de energie in exces. Cu o sursa monoenergetica, evenimentele din aceasta regiune sunt datorate radiatiilor gama de energii inalte si muonilor radiatiei cosmice din fondul natural. In spectrele complexe, impulsurile din aceasta regiune formeaza un fotopic datorat in primul rand evenimentelor Compton produse de radiatii gama de energii inalte.
G. Cresterea de la energii mici. Aceasta zona a spectrului apare de la zgomotul electronic de amplitudine joasa in sistemul de detectie si este procesat ca un puls de joasa amplitudine detectat. Zgomotul este filtrat electronic si acest efect nu domina in spectru. In spectrele complexe de radiatii gama, care contin multi fotoni de energii diferite, marginea Compton si picul de retroimprastiere au tendinta sa se "limpezeasca", aparand picuri de energie totala in zona relativ neteda a fondului Compton.
3. Rezolutia detectorului
Rezolutia unui detector reprezinta o masura a capacitatii acestuia de a analiza doua picuri foarte apropiate energetic. Parametrul utilizat pentru precizarea rezolutiei unui detector este largimea totala a fotopicului (de energie totala) la jumatate din inaltimea maxima (Full Width of the photopeak at Half its Maximum height; FWHM). Daca fotopicului i se poate atribui o gaussiana de forma standard, atunci FWHM este data de relatia:
FWHM = 2σ![]()
unde σ este parametrul de largime pentru gaussiana. Inalta rezolutie (FWHM mic) a detectorului face ca definirea individuala a picurilor apropiate sa fie foarte usoara si in acelasi timp extragerea zonei Compton este usurata deoarece reprezinta o mica fractiune din activitatea totala din regiunea picului. Cu cat spectrul de radiatii gama este mai complex cu atat este necesara o rezolutie energetica mai mare.
Detectorii cei mai utilizati in analizele nedistructive cu radiatii gama sunt scintilatorii cu NaI(Tl) si detectorul cu germaniu. Figura 7 ilustreaza spectrul de radiatii gama al plutoniului achizitionat cu detector de germaniu, cu multe detalii care se pierd in spectrul corespunzator achizitionat cu detectorul de NaI.
|
|
Fig. 7. Spectru de radiatii gama al unei probe de plutoniu cu 94,2% 239Pu, achizitionat cu un detector Ge(Li) de inalta rezolutie si cu un scintilator cu NaI. Energiile radiatiilor gama sunt date in keV.
Luand in considerare limitele statistice in precizia energetica, putem explica originea diferentelor in rezolutia energetica a diferitelor tipuri de detectori. Ideal, numarul sarcinilor electronice (n) produs in evenimentul de detectie primara depinde de energia cedata (E) si de valoarea medie a energiei necesara producerii unei perechi electron-ion (δ):
Variatia statistica intamplatoare a lui n este sursa principala a fluctuatiilor pulsului de amplitudine al energiei totale. Pentru unii detectori aceasta variatie statistica este mai mica decat valoarea teoretica cu un factor denumit factor Fano (F):
σ2(n) = Fn = FE/δ.
Acest efect provine din faptul ca o parte din energia pierduta de fotonul incident formeaza perechi de ioni, iar o parte se transforma in energie termica (incalzeste reteaua cristalina). Divizarea energiei in termica si de ionizare are un caracter statistic. Daca toata energia initiala ar fi utilizata pentru ionizare nu ar exista fluctuatii statistice ale lui n (F = 0). Daca probabilitatea de producere a perechii de ioni este mica, atunci fluctuatiile statistice sunt dominante F = 1. Pentru scintilatori factorul Fano este aproximativ egal cu unitatea, iar pentru detectorii cu germaniu, siliciu si gaze este aproximativ 0,15. Deoarece numarul purtatorilor de sarcina (n) este proportional cu energia cedata de fotoni partea statistica a rezolutiei energetice relative este data de relatia:
ΔEstat/E = 2,35σ(n)/n = 2,35[Fδ/E]1/2.
Δ2Etot = Δ2Eelect + Δ2Estat = α + βE.
Compararea rezolutiei energetice in regiunea radiatie X de energie joasa pentru detectori cu scitilatori, gaz si semiconductor este prezentata in figura 8.
|
|
Fig. 8. Compararea rezolutiei energetice intre scintilator NaI, contor proportional cu gaz si detector cu semiconductor Si(Li) pentru radiatia X primara a argintului.
4. Eficienta detectorului
Definitia eficientei absolute de detectie a fotonului este:
εtot = ![]()
Discutia se va axa numai pe evenimentele de energie totala si deci pe eficienta detectorului pentru fotopicul de energie totala. Aceasta eficienta totala poate fi exprimata ca un produs de patru factori:
εtot = εgeom εabsorb εproba εintr
εgeom = A/(4πr2)
unde A este aria sectiunii transversale a detectorului si r este distanta sursa detector. Acest factor este independent de energia fotonului.
Eficienta de absorbtie εabsorb tine cont de efectele din materialele care absorb o parte din radiatia incidenta inainte ca aceasta sa interactioneze cu volumul detectorului. Acest termen este deosebit de important (si trebuie sa fie << 1) pentru fotonii de energii joase, in cazul carora efectele de absorbtie sunt pronuntate. Matematic are expresia:
εabsorb = exp[ - Σμi(Eγ)ρixi]
unde μi, ρi si xi sunt coeficientul masic de absorbtie, densitatea si grosimea celui de al i-lea material care intervine intre volumul detector si emitatorul de radiatie, iar sumarea se face peste toate tipurile de materiale care intervin.
Eficienta probei εproba este echivalenta cu corectia de autoabsorbtie a probei. De exemplu pentru o foita de grosime x si transmisie T egala cu exp[-(μρx)p], eficienta probei este:
εproba = 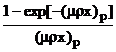 =
= ![]()
Acest factor depinde de compozitia fiecarei probe.
Eficienta intrinseca εintr reprezinta probabilitatea ca radiatia gama care patrunde in detector sa interactioneze si sa produca un puls in picul de energie totala. In termeni simpli aceasta eficienta provine din formula clasica a absorbtiei
εintr = 1 - exp(-μρx)
unde μ este coeficientul fotoelectric de atenuare masica, ρ si x sunt densitatea si grosimea materialului detector. Aceasta expresie simpla subestimeaza adevarata eficienta intrinseca deoarece picul de energie totala contine evenimente si din interactiunile multiple de imprastiere Compton. In general εintr este o functie dependenta puternic si de r datorita detectarii radiatiilor gama care nu sunt pe directia axei incidente a detectorului. Empiric εintr poate fi aproximat printr-o lege de tipul:
εintr = a![]() .
.
Eficienta detectorilor este masurata si cotata ca eficienta absoluta a fotopicului la detectia radiatiei gama de la o sursa punctiforma neatenuata. Deci, dependenta lor energetica este dominata de εintr la energii inalte si de εabsorb la energii joase; factorul geometric εgeom stabileste marimea totala a eficientei. Eficienta intrinseca si de absorbtie sunt puternic dependente de energia fotonului incident, fapt ilustrat in figurile 9 si 10 care prezinta dependenta energetica a eficientei de detectie pentru detector Ge(Li) planar si coaxial.
|
|
Fig. 9. Eficienta absoluta a picului de energie totala, pentru o sursa punctiforma situata la 54 mm de un detector Ge(Li) planar cu diametrul de 33 mm si grosime 6,8 mm. Punctele masurate provin in urma dezintegrarilor gama spontane si induse cunoscute. Scaderea eficientei pentru energii joase indica cresterea absorbtiei radiatiei gama de energii scazute in containerul detectorului si in alti absorbanti (εabsb). Descresterea eficientei pentru energii mari indica scaderea ratei de interactie in cristalul detector a radiatiilor gama de energii inalte (εintr). |
|
Fig. Analog cu figura 9, exceptand: detector coaxial Ge(Li) de 38 cm3 si sursa punctiforma situata la 83 mm de detector. |
Aceste figuri indica trei puncte generale:
1. Dependenta energetica puternica a eficientei totale produce o diferenta mare intre intensitatea fotonului inregistrat si cel emis. La efectuarea analizelor care implica compararea in intensitate a diferitelor radiatii gama trebuie sa se tina cont de corectia energetica a eficientei.
2. In analiza radiatiilor gama de energii joase se folosesc detectori cu volum subtire. Acestia optimizeaza eficienta de detectie in regiunile de energie joasa si reduce eficienta de detectie pentru radiatiile gama de energii inalte.
3. In analiza radiatiilor gama de energii inalte se folosesc detectori cu volum mare pentru a asigura eficienta adecvata radiatiilor mult mai penetrante. Se folosesc chiar si absorbanti la intrarea in detector pentru a reduce contributia la viteza de numarare a radiatiilor de energii joase.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |