PARAMERII CARATERISTICI PENTRU TRANSFORMARILE SIMPLE ALE GAZELOR PERFECTE

PARAMERII CARATERISTICI PENTRU TRANSFORMARILE SIMPLE ALE GAZELOR PERFECTE

1. Transformarea izocora

Transformarea izocora are loc la volum constant (fig. 1.12), fiind caracterizata de ecuatia:

Lucrul mecanic corespunzator variatiei de volum este dat de relatia:

Transformarea fiind izocora, volumul este constant, deci:

Lucrul mecanic tehnic se calculeaza cu relatia generala:

de unde rezulta:

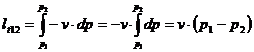
Caldura schimbata rezulta din ecuatia primului principiu al termodinamicii:

dq = dl + du;

cum dl=0 rezulta dq = du sau:

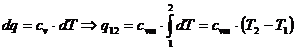
sau

unde c_vm este caldura specifica medie, la volum constant, presupusa a fi independenta de temperatura.

2. Transformarea izobara

Transformarea izobara are loc la presiune constanta (fig. 1.13), fiind caracterizata de ecuatia:

Lucrul mecanic corespunzator variatiei de volum este:

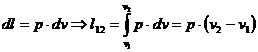
Lucrul mecanic tehnic rezulta din relatia de definitie:

Cum presiunea este constanta (dp = 0), rezulta l_t12 = 0.

Caldura schimbata intr-un proces izobar se determina din primul principiu al termodinamicii:

in care dp = 0, ceea ce ne conduce la:

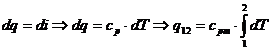
de unde:

sau

3. Transformarea izoterma

Transformarea izoterma are loc la temperatura constanta, ecuatia caracteristica fiind:

Lucrul mecanic corespunzator variatiei de volum este:

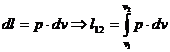
Din ecuatia generala a gazului obtinem:

iar lucrul mecanic va fi:

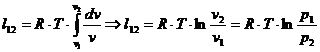
Lucrul mecanic tehnic se determina pornind de la relatia:

Din ecuatia termica de stare a gazului rezulta:

Inlocuind volumul specific obtinem:

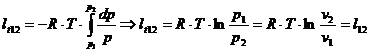
Caldura schimbata in procesul izoterm va fi:

dq = dl + du.

Dar du = c_p dT, iar procesul fiind izoterm dT = 0; rezulta deci dq = dl sau:

q₁₂ = l₁₂.

4. Transformarea adiabatica

Transformarea adiabatica se caracterizeaza prin absenta schimbului de caldura cu mediul inconjurator (dq = 0).

Din ecuatia primului principiu al termodinamicii dq = dl + du, pentru:

dq = 0, du = c_v dT, dl = p dv,

rezulta

si tinand cont ca   si ca c_p/c_v = k obtinem urmatoarele relatii caracteristice ale transformarii adiabatice:

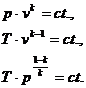
Lucrul mecanic corespunzator variatiei de volum rezulta din relatia dq=dl + du, in care dq=0, iar du = c_v dT, ceea ce ne conduce la:

sau, pentru , rezulta:

Lucrul mecanic tehnic rezulta din ecuatia primului principiu al termodinamicii sub forma , in care dq=0 si rezulta:

sau

Cum , rezulta in final:

5. Transformarea politropa

Este cea mai generala transformare, fiind caracterizata prin relatiile:

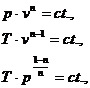
in care n este exponentul politropic. Valori particulare ale exponentului politropic permit obtinerea relatiilor caracteristice celorlalte transformari (fig. 1.15):

sindu-se insa exponentul politropic n in loc de exponentul adiabatic k:

Pentru calculul caldurii schimbate intr-un proces politropic se porneste de la relatia:

q₁₂ = l₁₂ + Du,

in care Du = c_vm (T₂-T₁) si ; in final rezulta:

sau