
Probleme la operarea de virgula flotanta
Pentru inceput,
sa ne referim la conventia de reprezentare a numerelor de virgula
flotanta, precum si la sistemul de notatii la care aderam.
Astfel, sa consideram un numar X, in notatie
stiintifica, de forma![]() si
sa specificam ca B este baza sistemului de numeratie cu valoare, in
cazul in care nu se precizeaza altceva, implicit egala cu 2, iar XM
si XE sunt numerele de virgula fixa reprezentand
mantisa, respectiv exponentul. Chiar daca acceptam conventiile
standardului IEEE 754, intrucat formatele acestuia prezinta campuri cu
numere variabile de biti, vom admite ca un cuvant pentru
reprezentarea unui numar de virgula flotanta este alcatuit,
de la stanga la dreapta, dintr-un bit alocat semnului, urmat de e
biti alocati exponentului si de m biti alocati
mantisei. In ceea ce priveste exponentul XE, acesta este un numar
binar intreg reprezentat in exces de (
si
sa specificam ca B este baza sistemului de numeratie cu valoare, in
cazul in care nu se precizeaza altceva, implicit egala cu 2, iar XM
si XE sunt numerele de virgula fixa reprezentand
mantisa, respectiv exponentul. Chiar daca acceptam conventiile
standardului IEEE 754, intrucat formatele acestuia prezinta campuri cu
numere variabile de biti, vom admite ca un cuvant pentru
reprezentarea unui numar de virgula flotanta este alcatuit,
de la stanga la dreapta, dintr-un bit alocat semnului, urmat de e
biti alocati exponentului si de m biti alocati
mantisei. In ceea ce priveste exponentul XE, acesta este un numar
binar intreg reprezentat in exces de (![]() ), care, particularizat pentru standardul IEEE pe 32
biti cu e = 8, consta in codul exces de 127. Prin conventie,
pentru a accepta exceptii asemanatoare cu cele care corespund
standardului IEEE 754, mai admitem restrictia valorica
), care, particularizat pentru standardul IEEE pe 32
biti cu e = 8, consta in codul exces de 127. Prin conventie,
pentru a accepta exceptii asemanatoare cu cele care corespund
standardului IEEE 754, mai admitem restrictia valorica![]() . Pe de alta parte, in ceea ce priveste mantisa
. Pe de alta parte, in ceea ce priveste mantisa![]() , ea este reprezentata de partea
fractionara a asa-numitului numar significand, de forma ( XM = 1* X*M) care este un numar binar in semn
marime cu bitul (1) de intreg ascuns. Acest bit implicit, menit a
creste precizia de reprezentare nu apare in mod explicit in forma
"impachetata" a numarului, cum se prezinta ea in calitate de
date de intrare, respectiv de rezultate la iesire. In vederea
operarii, numarul de virgula flotanta trebuie despachetat,
ceea ce implica corespunzatoarea inserare a respectivului bit. Mai
mentionam ca, in calitate de date de intrare, respectiv
rezultate la iesire, numerele de virgula flotanta se
prezinta in forma normalizata (implicand restrictia
1≤│1. X*M│<2), dar, pe parcursul
calculelor, ele sunt operate, uzual, in forma nenormalizata.
, ea este reprezentata de partea
fractionara a asa-numitului numar significand, de forma ( XM = 1* X*M) care este un numar binar in semn
marime cu bitul (1) de intreg ascuns. Acest bit implicit, menit a
creste precizia de reprezentare nu apare in mod explicit in forma
"impachetata" a numarului, cum se prezinta ea in calitate de
date de intrare, respectiv de rezultate la iesire. In vederea
operarii, numarul de virgula flotanta trebuie despachetat,
ceea ce implica corespunzatoarea inserare a respectivului bit. Mai
mentionam ca, in calitate de date de intrare, respectiv
rezultate la iesire, numerele de virgula flotanta se
prezinta in forma normalizata (implicand restrictia
1≤│1. X*M│<2), dar, pe parcursul
calculelor, ele sunt operate, uzual, in forma nenormalizata.
Odata stabilite conventiile de reprezentare, operatiile fundamentale de adunare, scadere, inmultire si impartire intre numerele de virgula flotanta X=XM*2XE si Y= YM*2YE sunt date de:
X + Y = (XM*2XE - YE + YM)* 2YE, unde XE ≤ YE
X - Y = (XM*2XE - YE - YM)* 2YE, unde XE ≤ YE (5.1)
X * Y = (XM* YM)* 2 XE + YE
X / Y = (XM / YM)* 2YE - XE
O prima constatare consta in faptul ca in (5.1) intervin doar operatii care se efectueaza asupra unor numere de virgula fixa. Apoi, mai remarcam ca, mai complicate in virgula fixa, inmultirea si impartirea sunt acum mai simple decat adunarea si scaderea, intrucat acestea implica o executie esalonata care prevede, mai intai, compararea (prin scadere) exponentilor, apoi, corespunzatoarea aliniere a numerelor significand si, in final doar, efectuarea operatiei propriu-zise (exemplificate aceste operatii in mai familiarul sistem zecimal, avem 7,936×108+3,158×1010 = (7,936×108-10+3,158)×1010=(0,07936+3,158)×1010=3,23736×1010)
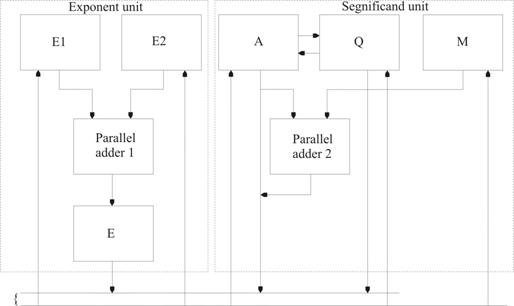
Fig.5.3
Din (5.1) rezulta ca asupra exponentilor se executa doar operatii de adunare si scadere pe cand asupra numerelor significand se executa toate operatiile fundamentale, de la adunare la impartire. Desigur, o structura de ALU de tipul celei din figura 5.1 ar putea acoperi toate operatiile enumerate, dar aceasta ar presupune serializarea acestora cu corespunzatoare degradari de performanta. Ca atare, solutia preconizata uzual pentru partea de aritmetica a unui ALU de virgula flotanta consta din apelarea la o configuratie cu doua subunitati una dedicata exponentilor si alta numerelor significand. Intre cele doua comunicatia poate fi asigurata doar prin intermediul magistralei, solutie denumita slab cuplata (loosely coupled) sau, pe langa magistrala exista un numar, in general restrans, de conexiuni directe, care asigura o comunicare rapida, dar costisitoare, solutie denumita strans cuplata (tightly coupled).
In fig. 5.2 este reprezentata o schema bloc corespunzatoare solutiei slab cuplate, urmand ca in paragraful urmator sa prezentam si o versiune cu cuplaj strans pentru o unitate de adunare in virgula flotanta. In figura avem unitatea de exponent constand din trei registre, doua (E1 si E2) pentru exponentii de intrare (XE si YE) si unul (E) pentru exponentul rezultat si, de asemenea, avem unitatea de significand cu configuratia asemanatoare celei din fig. 5.1.
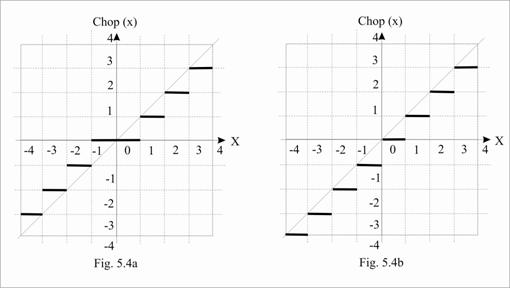
Fig.5.4
Dar, operarea in virgula flotanta se confrunta cu, in acest caz, importanta problema a rotunjirii (rouding) necesara pentru a converti valori de mare precizie sau rezultate ale unor calcule intermediare cu cifre suplimentare la formate de precizie mai scazuta in vederea memorarii si/sau extragerii rezultatelor finale. In conformitate cu standardul IEEE 754, avem 4 moduri de rotunjire [SeEv04], [Parh00], si anume: round to nearest even (rotunjire la cel mai apropiat numar par), round toward 0 (inward) (rotunjire spre zero, spre interior), round toward +∞ (upward) (rotunjire spre +∞, in sus) si round toward -∞ (downward) (rotunjire spre -∞ in jos).
Pentru a ne familiariza cu modurile de rotunjire, sa consideram numarul fara semnul X parte intreaga si parte fractionara, adica : X=xn-1xn-2 . x1x0.x-1x-2 . x-m care trebuie rotunjit la valoarea intreaga X*=x*n-1x*n-2 . x*1x*0 . Cea mai simpla metoda o constituie trunchierea (truncation & chopping) constand din renuntarea la biti suplimentari, adica X*1=xn-1xn-2 . x1x0. Pe de alta parte, este important de remarcat ca efectul trunchierii asupra numerelor reprezentate in semn-marire este diferit de cel asupra numerelor reprezentate in complement de doi. Deosebirile sunt puse in relief de dependentele din fig. 5.4 [Parh00]. Astfel, in fig. 5.4a se arata efectul trunchierii asupra unui numar in semn-marime, putand fi observat faptul ca marimea numarului trunchiat, sa o notam chop (X), este intotdeauna mai mica decat a numarului netrunchiat X, fapt pentru care tipul de rotunjire este "round toward 0".
Prin contrast, in fig.5.4b se arata efectul trunchierii asupra unui numar in complement de doi putand fi observat faptul ca valoarea numarului trunchiat, chop (X), este intotdeauna mai mica decat cea a numarului netrunchiat (X), fapt pentru care tipul de rotunjire este "round toward -∞". In ceea ce priveste rotunjirea de tipul "round to nearest" a lui X, pe care o notam rtn (X), daca numarul X este in semn-marime, o parte fractionara mai mica decat ½ este ignorata, in timp ce o parte fractionara egala sau mai mare decat ½ determina rotunjirea la valoarea intreaga mai mare urmatoare, dupa cum rezulta din fig.5.5a
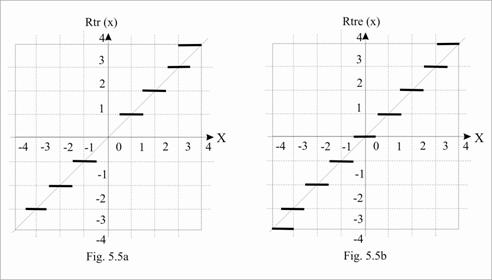
Fig.5.5
Daca aceasta regula este
aplicata la numere reprezentate in complement de doi, atunci la
fig.5.5a apare o modificare doar la valorile negative a lui X si anume
punctele se muta de la capetele din dreapta ale liniilor marcate
ingrosat la capetele din stanga. Indiferent de modul de reprezentare,
semn-marime sau complement de doi, prin atribuirea valorii de la mijlocul intervalului
(punctele din fig.5.5a, spre exemplu) la o anumita parte
fractionara (in cazul din fig.5.5a, la partea mai mare decat ½) se
creeaza un oarecare dezechilibru care poate crea probleme datorita acumularilor
de erori. Pentru a ne aduce mai aproape efectul acestui dezechilibru, sa
presupunem ca dorim rotunjirea numarului X = xn-1xn-2
. x1x0 . x--1x--2 la valoarea
intreaga X*=x*n-1x*n-2
. x*1x*0. In dependenta
de valorile celor 2 biti din partea fractionara avem
urmatoarele 4 cazuri impreuna cu erorile ε asociate lor : x-1x-2
= 00, rotunjire in jos (intrucat x-1=0, deci x-1x-2
< ½) si ε = 0; x-1x-2 = 01, rotunjire in jos
si ![]() ; x-1x-2 = 10, rotunjire in sus si
; x-1x-2 = 10, rotunjire in sus si
![]() ; x-1x-2=11 rotunjire in sus si
; x-1x-2=11 rotunjire in sus si![]() . Daca cele patru cazuri sunt echiprobabile,
exista o eroare medie
. Daca cele patru cazuri sunt echiprobabile,
exista o eroare medie ![]() . In practica se dovedeste ca
probabilitatea de a obtine valoare corespunzatoare mijlocului
intervalului (x-1x-2
= 10) este mai mare decat celelalte, inrautatind
suplimentar dezechilibrul rezultat, in cazul nostru, erorii
. In practica se dovedeste ca
probabilitatea de a obtine valoare corespunzatoare mijlocului
intervalului (x-1x-2
= 10) este mai mare decat celelalte, inrautatind
suplimentar dezechilibrul rezultat, in cazul nostru, erorii ![]()
O cale de surmontare a problemei sesizate o reprezinta rotunjirea intotdeauna la un intreg par (sau impar), determinand astfel ca valorile din mijloc (x-1x-2 = 10) sa fie rotunjite in sus, respectiv in jos, cu aceasi probabilitate. In fig.5.5b se prezinta rotunjirea numerelor X, reprezentate in semn-marime, prin modul "round to nearest" la valori rtne (X) . In ceea ce priveste numerele reprezentate in complement de doi, dependenta din fig. 5.5b nu se modifica intrucat, spre exemplu, (-1.5) se rotunjeste la (-2) corespunzator ambelor reprezentari. Standardul IEEE 754 prefera solutionarea cazurilor "jumatate de drum" (halfway) prin apelarea la modul "round to nearest even" in detrimentul modului "round to nearest odd" (de rotunjire la cel mai apropiat numar impar).
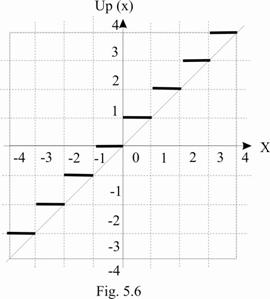
In fine, conform standardului IEEE 754, mai avem un mod de rotunjire, anume, "round toward +∞" (fig. 5.6), caracterizat prin faptul ca valoarea rotunjita a numarului X, pe care o notam cu up (X) (de la upward-directed rounding), se obtine prin alegerea intotdeauna a valorii de intreg capatul superior al intervalului caruia ii apartine X.
In unele aplicatii, cum ar fi acelea corespunzatoare aritmeticii intervalelor (interval arithmetic) [Erha 04][Kuli 02][Parh 00], este necesar ca erorile de calcul sa fie fortate intr-o anumita directie cunoscuta. Spre exemplu, daca dorim sa evaluam o limita superioara (upper bound) pentru o anumita cantitate, atunci doar valorile mai mari decat cele corecte sunt acceptate, ceea ce corespunde rotunjirii in sus, adica, "round toward +∞". Evident, daca, in mod asemanator, dorim sa evaluam o limita inferioara (lower bound) pentru o anumita cantitate, atunci doar valorile mai mici decat cele corecte sunt acceptate, ceea ce corespunde anterior prezentatei rotunjiri in jos, adica "round toward -∞" (fig.5.4b). Ambele moduri de rotunjire se aplica in aritmetica intervalelor.
In cele ce
urmeaza, sa analizam mai in amanunt modul in care se
realizeaza rotunjirea [Kuli 02]. Astfel, daca ne referim la
adunare/scadere, conform cu (5.1), operatia propriu-zisa este
precedata de compararea exponentilor si corespunzatoarea
aliniere a numerelor significand. Daca admitem ca dimensiunea
campului de mantisa este de m biti si daca, avem,
ca in (5.1), XE ≤ YE , atunci, in
cazul in care avem YE - XE
≥ m, rezultatul suma va fi egal cu unul dintre operanzi, in cazul nostru Y. Daca insa YE - XE < m, atunci,
in urma deplasarii la dreapta a unui operand - in cazul nostru X-, se
efectueaza operatia propriu - zisa, care in cazul executiei
acesteia in mod exact, necesita, in caz defavorabil, un sumator de (2m-1)
biti, dezavantajos atat prin prisma costului, cat mai ales a
perfomantei. Dar solutia adoptata nu se bazeaza pe
algoritmul ideal constand din efectuarea in mod exact a sumei si
ulterioara rotunjire, ci se apeleaza la un sumator de doar m biti
si un numar de biti suplimentari situati la dreapta lsb-ului
operandului deplasat, in care sa fie retinuta, in urma
shift-arii, informatia necesara pentru ulterioara rotunjire.
Aceasta se impune astfel realizata incat sa nu se piarda din
precizie in raport cu executia operatiei conform algoritmului ideal.
Numarul acestor biti aditionali fata de cei m
ai mantisei este de trei si ei au denumiri consacrate, si anume g,r si s. Primul bit, situat in urma shift-arii, la dreapta lsb-ului
mantisei deplasate - admitem ![]() , se numeste bit de gardare (guard bit) si este
notat cu g, fiind ultimul bit care,
in procesul de aliniere a mantiselor, paraseste cei m
biti alocati initial lui
, se numeste bit de gardare (guard bit) si este
notat cu g, fiind ultimul bit care,
in procesul de aliniere a mantiselor, paraseste cei m
biti alocati initial lui ![]() . Facand abstractie de semnele operanzilor, in fig.
5.7 se prezinta situatia celor doua mantise inainte de aliniere
(before mantissa alignment), resptectiv dupa aliniere (after mantissa
alignment), unde a fost admis ca deplasarea la dreapta s-a realizat cu
. Facand abstractie de semnele operanzilor, in fig.
5.7 se prezinta situatia celor doua mantise inainte de aliniere
(before mantissa alignment), resptectiv dupa aliniere (after mantissa
alignment), unde a fost admis ca deplasarea la dreapta s-a realizat cu ![]() -
- ![]() =
=![]() biti, cand g
coincide cu
biti, cand g
coincide cu ![]() . Cel de-al doilea bit, situat imediat la dreapta lui g coincident in exemplul din fig. 5.7 cu
. Cel de-al doilea bit, situat imediat la dreapta lui g coincident in exemplul din fig. 5.7 cu
![]() , se numeste bit de rotunjire (round bit) si este
notat cu r, el fiind bitul care
paraseste cei m biti alocati
initiali lui
, se numeste bit de rotunjire (round bit) si este
notat cu r, el fiind bitul care
paraseste cei m biti alocati
initiali lui ![]() inaintea lui g. In fine, cel de-al treilea bit,
denumit de "lipitura" (sticky bit), este notat cu s si el are valoarea obtinuta in urma operatiei
logice OR, efectuata, in procesul de deplasare, intre cei mai
semnificativi, in cazul nostru (
inaintea lui g. In fine, cel de-al treilea bit,
denumit de "lipitura" (sticky bit), este notat cu s si el are valoarea obtinuta in urma operatiei
logice OR, efectuata, in procesul de deplasare, intre cei mai
semnificativi, in cazul nostru (![]() ), biti ai lui
), biti ai lui ![]() si in general intre bitii care parasesc
cei m
biti alocati initial lui
si in general intre bitii care parasesc
cei m
biti alocati initial lui ![]() , exceptandu-i pe g
si r.
, exceptandu-i pe g
si r.

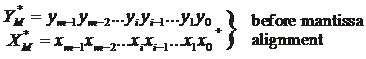
![]()

![]() Fig.5.7
Fig.5.7
![]()
Daca se efectueaza o aliniere la dreapta de un bit, g va retine acest bit si nu se va pierde din precizie, astfel ca g se poate spune ca "gardeaza" impotriva pierderii de precizie. La o aliniere pentru deplasarea la dreapta cu doi sau mai multi biti, significand-ul deplasat la dreapta va avea marimea apartinand intervalului valoric [0, ½). Intrucat significand-ul operandului nedeplasat este cuprins, asa cum este cunoscut, in intervalul valoric [1,2), situatia cea mai defavorabila apare atunci cand trebuie facuta diferenta dintre significand-ul nedeplasat si cel deplasat, pentru ca marimea acestuia rezulta ca poate apartine intervalului [1/2,2). Dar aceasta are drept consecinta, intr-o prima instanta, ca, in vederea normalizarii rezultatului, acesta trebuie deplasat la stanga cu cel mult o pozitie binara, astfel ca, intr-o a doua instanta, bitul g este adecvat si, pentru acest caz, in scopul protejarii impotriva pierderii de precizie.
In cazul cand are loc intr-adevar o shiftare la stanga cu o pozitie binara, g devenind lsb-ul mantisei, determinarea sensului de rotunjire (in sus, respectiv in jos) a significand-ului rezultant se realizeaza in functie de valoarea bitului r. Astfel, daca r = 0, deci partea eliminata prin deplasare la dreapta este mai mica decat 1/2, rotunjirea se face in jos, iar daca r = 1, partea eliminata prin deplasare la dreapta este mai mare sau egala cu 0, rotunjirea se face in sus.
Mai trebuie stabilit daca partea eliminata prin deplasare la dreapta este sau nu egala exact cu ½, intrucat anumite moduri de rotunjire uziteaza de aceasta informatie. Ea este furnizata de bitul s care, reprezentand rezultatul operarii OR a tuturor bitilor din partea dreapta a lui r, indica faptul ca atunci cand r=1 si s=1, marimea partii eliminate depaseste valoarea de ½, iar atunci cand r=1 si s=0, respectiva marime este exact egala cu ½. Cu alte cuvinte, daca avem 5 biti eliminati in procesul de aliniere, atunci bitul s va fi setat la valoarea rezultata in urma operarii OR a celor 3 biti care trec, in cursul deplasarii la dreapta, de pozitiile g si r.
Sa
admitem ca in urma efectuarii unei operatii, sa
consideram de adunare, a rezultat significand-ul preliminar ![]() , cu corespunzatoarea mantisa
, cu corespunzatoarea mantisa ![]() . Intrucat
. Intrucat ![]() poate fi obtinut in forma nenormalizata,
inainte de a trece la operatia de rotunjire,
poate fi obtinut in forma nenormalizata,
inainte de a trece la operatia de rotunjire, ![]() trebuie supus la corespunzatoare deplasari in
vederea normalizarii, evident, cu obligatorii ajustari de exponent. In urma procesului de normalizare,
bitii de interes pentru rotunjire sunt cei de round - situat imediat la
dreapta bitului lsb al significand-ului normalizat - pe care il notam cu
R, si cel de sticky - reprezentand rezultatul operatiei OR catre
toti bitii situati la dreapta bitului lsb al significand-ului
normalizat exceptandu-l pe primul, adica pe R - pe care il notam cu
S. Luand in consideratie toate cazurile potentiale de normalizare,
obtinem expresiile pentru R si S prezentate in fig. 5.8.
trebuie supus la corespunzatoare deplasari in
vederea normalizarii, evident, cu obligatorii ajustari de exponent. In urma procesului de normalizare,
bitii de interes pentru rotunjire sunt cei de round - situat imediat la
dreapta bitului lsb al significand-ului normalizat - pe care il notam cu
R, si cel de sticky - reprezentand rezultatul operatiei OR catre
toti bitii situati la dreapta bitului lsb al significand-ului
normalizat exceptandu-l pe primul, adica pe R - pe care il notam cu
S. Luand in consideratie toate cazurile potentiale de normalizare,
obtinem expresiile pentru R si S prezentate in fig. 5.8.
Sunt prezentati
ultimii doi biti ai mantisei ![]() (fig. 5.7) inainte si dupa deplasare la dreapta cu
un bit (fig. 5.8a), la stanga cu un bit (fig. 5.8b), la stanga cu doi biti
(fig. 5.8c), caz care corespunde si unei deplasari cu mai multi
biti la stanga, iar in fig. 5.8d este data situatia cand
(fig. 5.7) inainte si dupa deplasare la dreapta cu
un bit (fig. 5.8a), la stanga cu un bit (fig. 5.8b), la stanga cu doi biti
(fig. 5.8c), caz care corespunde si unei deplasari cu mai multi
biti la stanga, iar in fig. 5.8d este data situatia cand ![]() este deja normalizat, nemai fiind necesara deplasarea sa.
Astfel, se poate remarca, spre exemplu, ca atunci cind ZM*este
shift-at, in procesul de normalizare, cu un bit la dreapta (fig. 5.8a), R
devine egal cu bitul lsb al significand-ului
este deja normalizat, nemai fiind necesara deplasarea sa.
Astfel, se poate remarca, spre exemplu, ca atunci cind ZM*este
shift-at, in procesul de normalizare, cu un bit la dreapta (fig. 5.8a), R
devine egal cu bitul lsb al significand-ului ![]() nedeplasat, iar S este obtinut prin operatia OR
efectuata intre vechiul s
si bitii g si r. Un caz aparte il reprezinta cel
din fig. 5.8c cand nu este necesara rotunjirea intrucat cazul cand
nedeplasat, iar S este obtinut prin operatia OR
efectuata intre vechiul s
si bitii g si r. Un caz aparte il reprezinta cel
din fig. 5.8c cand nu este necesara rotunjirea intrucat cazul cand ![]() este deplasat, la
normalizare, cu doi sau mai multi biti la stanga corespunde
evaluarii exacte a significand-ului rezultat, situatie in care se
conserva intreaga precizie. Mai mentionam ca analize similare
pot fi intreprinse si relativ la alte operatii, cum ar fi
inmultirea, asa cum se va vedea.
este deplasat, la
normalizare, cu doi sau mai multi biti la stanga corespunde
evaluarii exacte a significand-ului rezultat, situatie in care se
conserva intreaga precizie. Mai mentionam ca analize similare
pot fi intreprinse si relativ la alte operatii, cum ar fi
inmultirea, asa cum se va vedea.
Cu aceste
precizari relativ la ajustarile bitilor R si S, sa
trecem la efectiva implementare a modurilor de rotunjire. Astfel, daca
avem un rezultat normalizat pozitiv, atunci il putem rotunji "to nearest even"
prin tatonarea mai intai a valorii bitului R, care daca este egal cu 0,
determina lasarea neschimbata a rezultatului. In aceeasi
situatie ne aflam daca bitii lsb ai rezultatului
normalizat, sa-l notam ![]() =0, rezultatul normalizat este par si el trebuie sa
ramana par, conform cu cele din fig. 5.5b, si atunci cand R=1
si S=0. Cu alte cuvinte, considerand lucrurile invers, daca avem
indeplinita conditia logica
=0, rezultatul normalizat este par si el trebuie sa
ramana par, conform cu cele din fig. 5.5b, si atunci cand R=1
si S=0. Cu alte cuvinte, considerand lucrurile invers, daca avem
indeplinita conditia logica ![]() (operatia AND
este notata cu "
(operatia AND
este notata cu "![]() " si
operatia OR, pentru a o distinge de + (add), este notata or) atunci,
in vederea rotunjirii la valoarea significand-ului normalizat, il notam cu
" si
operatia OR, pentru a o distinge de + (add), este notata or) atunci,
in vederea rotunjirii la valoarea significand-ului normalizat, il notam cu
![]() , se adauga o unitate binara (la pozitia
bitului lsb,
, se adauga o unitate binara (la pozitia
bitului lsb, ![]() ). La o concluzie asemanatoare se poate ajunge,
relativ la acelasi mod de rotunjire, si pentru numerele significand
normalizate negative [Omon94].
). La o concluzie asemanatoare se poate ajunge,
relativ la acelasi mod de rotunjire, si pentru numerele significand
normalizate negative [Omon94].
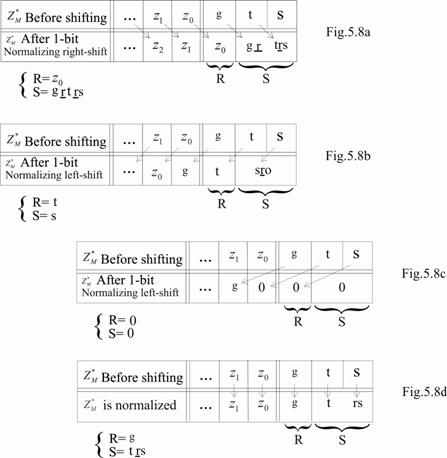
Fig.5.8
In ceea ce priveste modul de rotunjire "toward 0", conform cu cele din fig. 5.4a, fiind obtinut prin trunchiere, nu implica nici un pic de ajustare a significand-ului normalizat.
Pe
de alta parte, daca ne referim la modurile de rotunjire "toward
+∞", respectiv "toward -∞", atunci conform cu cele din fig. 5.6,
respectiv fig. 5.4b, adunarea unei unitati binare (la pozitia
bitului lsb, ![]() ) la significand-ul normalizat
) la significand-ul normalizat ![]() , are loc cand este indeplinita conditia
logica R+S=1 pentru
, are loc cand este indeplinita conditia
logica R+S=1 pentru ![]() (round toward +∞),
respectiv pentru
(round toward +∞),
respectiv pentru ![]() (round toward -∞).
Sintetizand cele expuse
relativ la modurile de rotunjire corespunzatoare normelor IEEE,
obtinem regulile date in tabelul din fig. 5.9.
(round toward -∞).
Sintetizand cele expuse
relativ la modurile de rotunjire corespunzatoare normelor IEEE,
obtinem regulile date in tabelul din fig. 5.9.
|
Rounding mode |
ZM ≥ 0 |
ZM < 0 |
|
toward -∞ |
If (P or S=1) then ZMN +1 |
|
|
toward 0 | ||
|
toward + ∞ |
If (R or S) then ZMN +1 | |
|
toward the nearest even |
If (R( zon or S) =1) Then ZMN + 1 |
Fig.5.9
Absenta unor marcaje din tabel trebuie interpretata in sensul ca rezultatul obtinut in urma normalizarii ramane nemodificat. Mai mentionam ca, efectuand rotunjirea dupa regulile din fig. 5.9, este posibil sa se obtina cout (carry out) din rangul msb al sumatorului, ceea ce implica inca o shift-are, la dreapta, a significand-ului rotunjit, impreuna cu corespunzatoarea ajustare a exponentului.
Pe langa problema
rotunjirii, operarea in virgula flotanta se confrunta si cu
cea a tratarii exceptiilor. Sub acest aspect, standardul IEEE
defineste cinci exceptii asociate cu depasirea (overflow),
sub depasirea (underflow), impartirea la 0 (divide - by -
0), o operatie invalida (invalid operation) sau cu un rezultat
inexact (inexact result) [HePa03][Parh00]. La aparitia lor, fiecare din
aceste exceptii seteaza un fanion (flag) si returneaza o
valoare speciala - de tipul ± ∞, ± 0 sau NaN (not a number) - cu
care calculele continua. In cazul cand o astfel de valoare speciala
apare in calitate de operand intr-o operatie aritmetica, rezultatul
acesteia este specificat in baza unor reguli definite care fac parte din
standard. Astfel, spre exemplu, NaN + numar
ordinar = NaN, ![]() numar ordinar
=
numar ordinar
= ![]() sau numar ordinar
sau numar ordinar ![]() (
(![]() ) =
) = ![]() 0.
0.
Dupa cum am vazut, valorilor speciale li se aloca coduri aparte permitand astfel ca exceptiile sa se propage pana la terminarea calculelor si sa nu determine oprirea, abandonarea acestora. Implementarea mecanismelor de exceptie poate include, pentru fiecare din cele 5 tipuri de mai sus, cate un program de tratare a exceptiei, un asa numit trap handler [Erha04], care poate fi apelat atunci cand este autorizat.
Exceptiile de overflow si underflow sunt simple de detectat prin scheme care urmaresc ajustarea exponentilor. Overflow-ul poate aparea doar atunci cand, in vederea normalizarii, se impune efectuarea unei deplasari la dreapta sau cand aceasta din urma este urmata de o rotunjire care a provocat aparitia unui cout Pe de alta parte, underflow-ul poate aparea doar atunci cand normalizarea revendica efectuarea de deplasari la stanga.
In ceea ce priveste divide-by-0, flag-ul asociat acestei exceptii este setat pe 1 daca avem de impartit un numar ordinar la zero, situatie cand, functie de semnul numaratorului, se returneaza (+∞) sau (-∞). Daca insa intervine o extragere de radical dintr-un operand negativ, atunci se seteaza pe 1 flag-ul de "invalid", fiind returnat, in vederea continuarii calculelor, NaN. De altfel, exceptia de operatie invalida apare nu doar la extragerea de radical dintr-un numar negativ, ci si la adunare, cand avem (+∞) + (-∞), sau la inmultire, cand avem 0*∞, sau la impartire, cand avem 0/0 sau ∞/∞. Uzual, exceptiile "invalid operation" returneaza valoarea speciala NaN si ele sunt tratate de schemele de despachetare, respectiv impachetare din, respectiv in, formatul standard IEEE.
In fine, exceptia
de "inexact", una neuzuala, se impune semnata atunci cand rezultatul
unei operatii sau conversii nu poate fi reprezentat in mod exact si
el trebuie rotunjit. Dar astfel de situatii apar foarte frecvent, deci
"inexact" nu constituie, in mod real, o conditie exceptionala.
In calitate de exemplu, sa consideram, ca avem alocati m=3
biti pentru mantisa si avem de inmultit (![]() ) cu (
) cu (![]() ) cand obtinem produsul
) cand obtinem produsul ![]() . Intrucat m=3 si, pe de alta parte, R=0 si
S=1, rezulta ca rezultatul rotunjit este
. Intrucat m=3 si, pe de alta parte, R=0 si
S=1, rezulta ca rezultatul rotunjit este ![]() , ceea ce determina setarea pe 1 a flag-ului de "inexact
result". In particular, ar mai fi de observat ca rezultatul obtinut este
si denormalizat [ScST 05]. Dupa cum a fost deja prezentat, numerele
denormalizate sunt de definite para hidden bit de 1 si cu cea mai
mica valoare posibila pentru exponent, ele fiind adoptate pentru a
face mai putin abrupt efectul de underflow. Cu alte cuvinte, unele valori
mici, care nu sunt reprezentabile ca numere normalizate si deci ar trebui
rotunjite la 0, atunci cand sunt intalnite pe parcursul calculelor pot fi
reprezentate mai precis ca numere denormalizate. Prin urmare, avem de-a face cu
un "gradual underflow" (uneori denumit si "graceful underflow" [Parh00])
care impune precautii speciale la setarea flag-ului exceptiei de
underflow. Ar mai fi de
mentionat ca implementarea mecanismului de underflow gradual conduce
la penalitati de performanta si cost, astfel ca
unele implementari nu accepta numere denormalizate optand pentru mai
rapidul, decat mai putin precisul, asa numit mod de functionare
"flush to zero" [ScST 05].
, ceea ce determina setarea pe 1 a flag-ului de "inexact
result". In particular, ar mai fi de observat ca rezultatul obtinut este
si denormalizat [ScST 05]. Dupa cum a fost deja prezentat, numerele
denormalizate sunt de definite para hidden bit de 1 si cu cea mai
mica valoare posibila pentru exponent, ele fiind adoptate pentru a
face mai putin abrupt efectul de underflow. Cu alte cuvinte, unele valori
mici, care nu sunt reprezentabile ca numere normalizate si deci ar trebui
rotunjite la 0, atunci cand sunt intalnite pe parcursul calculelor pot fi
reprezentate mai precis ca numere denormalizate. Prin urmare, avem de-a face cu
un "gradual underflow" (uneori denumit si "graceful underflow" [Parh00])
care impune precautii speciale la setarea flag-ului exceptiei de
underflow. Ar mai fi de
mentionat ca implementarea mecanismului de underflow gradual conduce
la penalitati de performanta si cost, astfel ca
unele implementari nu accepta numere denormalizate optand pentru mai
rapidul, decat mai putin precisul, asa numit mod de functionare
"flush to zero" [ScST 05].
O ultima remarca o facem relativ la detectia unui rezultat zero si codificarea acestuia intrucat el nu poate fi reprezentat ca un numar significand normalizat. In formatul standard IEEE, zero are o reprezentare constand doar din biti, exceptand bitul de semn care poate fi pozitiv (0) sau negativ (1).
Pe langa problemele rotunjirii si tratarii exceptiilor, ar mai fi si cea a preciziei reprezentarii. Astfel, pe langa formatele pe 32 de biti, denumit si "single/short", respectiv pe 64 de biti, denumit si "double/long", standardul IEEE defineste si formate extinse (extended formats) [Erha04] [HePa03], care permit implementarilor cu aceste formate sa efectueze calcule in precizie mai ridicata reducand efectul erorilor acumulate. Cele doua formate extinse constau din single-extended cu ≥ 11 biti pentru exponent si ≥ 32 biti pentru significand (deplasamentul bias nu este specificat, dar domeniul de exponent trebuie sa fie inclus in intervalul [-1022, 1023]) si din double -extended cu ≥ 15 biti pentru exponent si ≥ 64 biti pentru significand (deplasamentul bias nu este specificat, dar domeniul de exponent trebuie sa fie inclus in intervalul [-16382, 16383]). Legat de formatele extinse, mentionam ca ele isi dovedesc utilitatea la controlul propagarii erorilor atunci cand mai multe operatii aritmetice se executa in secventa. Astfel sa presupunem ca avem de adunat mai multe numere de virgula flotanta, situatie in care, prin prisma diminuarii erorilor computationale, este favorabil sa fie adunate, pe de o parte, valorile pozitive si, pe de alta parte, valorile negative, iar in final sa fie adunate cele doua subtotaluri, daca avem, conjunctural, foarte multe numere de adunat, este posibil ca la calculul unuia sau ambelor subtotaluri sa obtinem overflow. In situatia cand apelam la un format extins (single extended pentru operanzi de simpla precizie, respective double extended pentru operanzi de dubla precizie), probabilitatea de aparitie a overflow-ului se reduce in mod consistent.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |