ALTE EXEMPLE DE ALGORITMI ITERATIVI
E1. Determinati valoarea unui depozit (cu termen dupa 12 luni si adaugarea dobanzii la depozit) dupa n ani de zile, stiind valoarea initiala si dobanda anuala.
citeste v0,dob,n *de exemplu, 500, 10, respectiv 5
v v0 *valoarea initiala a depozitului
![]() pentru i=1,n repeta *valoare depozit
dupa al i-lea an
pentru i=1,n repeta *valoare depozit
dupa al i-lea an
v v + v*dob/100
*la vechea val se adauga dob aferenta vechii valori a dep
scrie v *valoarea finala
E2. (calculul sumelor)
Enuntul problemei: Pentru un intreg n≥1
dat, sa se calculeze valoarea sumei
S = 1+2+3++n,
fara a folosi formula de calcul direct S = n(n+1)/2.
Metoda de
rezolvare Suma se poate scrie restrans S =![]()
 Algoritmul general pentru determinarea
unei sume scris restrans S =
Algoritmul general pentru determinarea
unei sume scris restrans S =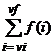 este urmatorul:
este urmatorul:
se initializeaza variabila S cu 0.
pentru i = vi, vi+1,.., vf se face S ← S + f(i) (adica la vechea valoare a sumei se adauga valoarea curenta din suma scrisa restrans).
Daca variabila S se declara global, primul pas nu mai este necesar pentru ca orice variabila globala declarata intr-un program C/C++ se initializeaza automat cu 0. Acest lucru nu mai este valabil insa daca variabila S este declarata local in functia "main" sau in alte functii.
Variabila S se poate declara de tip intreg.
daca se declara in C/C++ de tip "int", pentru n = 256 se depaseste valoarea maxima a domeniului "int" care este 32767;
daca se declara de tip "unsigned int", pentru n = 362 se depaseste valoarea maxima a domeniului "unsigned int" care este 65535;
daca se declara de tip "long", se depaseste valoarea maxima a domeniului "long" care este 2147483647 pentru n = 65535, insa cum n este declarat de tip "int" acest caz nu este posibil.
Descrierea algoritmului in pseudocod
citeste n
S *orice suma se initializeaza cu 0
![]() pentru i=1,n repeta
pentru i=1,n repeta
S S + i *la suma anterioara se aduna val curenta
scrie S
Descrierea algoritmului in C++:
#include<conio.h>
#include<iostream.h>
int n,i,S; //orice var globala se initializeaza cu 0
void main()
E3.
Enuntul problemei: Pentru un n≥2 intreg dat, sa se calculeze sumei S = 2 + 4 + 6 + + n.
Metoda de rezolvare: Comparativ cu suma de la programul anterior, de data aceasta "for"-ul de la algoritmul de calcul al sumei are pasul 2.
Descrierea algoritmului in pseudocod
citeste n
S
![]() pentru i=2,n,2 repeta
pentru i=2,n,2 repeta
S S + i
scrie S
Descrierea algoritmului in pseudocod in C++:
#include <conio.h>
#include <iostream.h>
int n,i,S;
void main()
E4. (determinarea valorii unui produs)
Enuntul problemei: Pentru un n≥0 intreg dat, sa se calculeze n .
Metoda de rezolvare Cum n! = 1 n, putem scrie
restrans n! = ![]() .
.
Algoritmul
general pentru determinarea unui produs scris restrans P =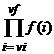 este
urmatorul:
este
urmatorul:
se initializeaza variabila P cu 1
pentru i = vi, vi+1,.., vf se face P ← P f(i).
In cazul
nostru, pentru ca initializarea se face cu 1 si aceasta valoare
reprezinta chiar 1! si 0!,
"for"-ul de la pasul 2 poate incepe de la 2.
Implementarea acestui algoritm in C/C++ trebuie sa tina cont de tipurile de date pe care le descriem mai jos.
Tipurile intregi din C/C++ sunt:
|
Tip |
Descriere |
Dimensiunea zonei de memorie ocupata |
Domeniul de valori |
|
char, signed char |
8 biti |
[-128, 127] |
|
|
unsigned char |
8 biti |
[0, 255] |
|
|
int, signed int, short int, signed short int |
intreg binar cu semn reprezentat prin complement fata de 2 |
16 biti |
[-32768, 32767] |
|
unsigned int, unsigned short int |
intreg binar fara semn |
16 biti |
[0, 65535] |
|
long, signed long |
intreg cu semn in dubla precizie |
32 biti |
[-231, 231-1] (231 = 2147483648) |
|
unsigned long |
intreg fara semn |
32 biti |
[0, 232-1] (232-1 = 4294967295) |
Tipurile reale din C/C++ sunt:
|
Tip |
Descriere |
Dim.zonei de memorie ocupata |
Domeniul de valori |
|
float |
numar real reprezentat in virgula flotanta in simpla precizie |
32 biti |
valorile absolute ale acestora (exceptand valoarea 0) sunt
in intervalul |
|
double |
numar real reprezentat in virgula flotanta in dubla precizie |
64 biti |
valorile absolute ale acestora (exceptand valoarea 0) sunt
in intervalul |
|
long double |
numar real reprezentat in virgula flotanta in dubla precizie |
80 biti |
valorile absolute ale acestora (exceptand valoarea 0) sunt in intervalul [3.4*10-4932, 1.1*104932] |
Cum valoarea factorialului creste foarte repede, trebuie acordata mare atentie declararii variabilei care se foloseste pentru determinarea factorialului:
daca se declara de tip int, pentru n = 8 se depaseste valoarea maxima a domeniului int care este 32767;
daca se declara de tip unsigned int, pentru n = 9 se depaseste valoarea maxima a domeniului unsigned int care este 65535;
daca se declara de tip long sau unsigned long, se depaseste valoarea maxima a domeniului care este 2147483647 respectiv 4294967295 pentru n = 13.
atunci se poate declara de tip real, de exemplu float, afisarea facandu-se cu 0 zecimale.
Descrierea algoritmului in pseudocod
citeste n *n trebuie sa fie mai mare sau egal ca 0
p *orice produs se initializeaza cu 1
![]() pentru i = 2,n repeta
pentru i = 2,n repeta
p p*i *produsul anterior se inmult cu val curenta i
scrie p
Descrierea algoritmului in C++:
#include<conio.h>
#include<iostream.h>
int n,i;
float P;
void main()
E5*.
Enuntul problemei: Sa se afiseze 1!, 2!, ., n!, pentru n≥1 intreg citit de la tastatura.
Metoda de rezolvare Algoritmul este urmatorul:
citeste n *n trebuie sa fie mai mare sau egal ca 1
![]() pentru k = 1,n,1 repeta * vrem sa calculam k!
pentru k = 1,n,1 repeta * vrem sa calculam k!
k_fact
![]() pentru i = 2,k,1 repeta
pentru i = 2,k,1 repeta
k_fact k_fact*i
scrie k_fact *pe rand nou
Pentru implementarea algoritmului in C/C++, cum numarul de randuri ale unui ecran text este 25 (sau 43 sau 50 in cazul in care setarea implicita acestuia este schimbata), daca valoarea lui n este mai mare trebuie facuta derulare pagina cu pagina, in caz contrar se poate vizualiza doar ultima pagina de ecran.
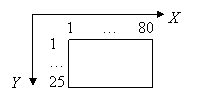
Pentru aceasta se poate folosi functia wherey() care da valoarea liniei pe care se afla cursorul in ecranul de rulare la un moment dat si poate avea valori intre 1 si 25. Daca s-a ajuns la randul 25 atunci cerem utilizatorului sa apese o tasta, apoi se sterge ecranul, cursorul revenind pe linia intai si se reia afisarea.
Descrierea algoritmului in C++:
#include<iostream.h>
#include<conio.h>
int n,i,k;
float k_fact;
void main()
cout<<endl<<k<<'! = '<<k_fact;
}
getch();
}
E6.
Enuntul problemei: Sa se calculeze Pn, Ank si Cnk, pentru n, k ≥ 0, n ≥ k intregi, citite de la tastatura.
Metoda de rezolvare Reamintim ca:
Pn = 1 ∙ 2 ∙ .
∙ n = n! = ![]()
![]() =
= ![]() = (n - k
+ 1) ∙ (n - k + 2) ∙.∙ n =
= (n - k
+ 1) ∙ (n - k + 2) ∙.∙ n = 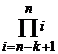
![]()
![]()
![]() =
= ![]() =
= ![]() =
= ![]()
Descrierea algoritmului in pseudocod
citeste n,k *n,k≥0, n≥k
perm
![]() pentru i = 2,n,1 repeta
pentru i = 2,n,1 repeta
perm perm*i
aranj
![]() pentru i = n-k+1,n,1 repeta
pentru i = n-k+1,n,1 repeta
aranj aranj*i
k_fact
![]() pentru i = 2,k,1 repeta
pentru i = 2,k,1 repeta
k_fact k_fact*i
comb aranj/k_fact
scrie perm,aranj,k_fact
Descrierea algoritmului in C+:
#include <iostream.h>
#include <conio.h>
int n,i,k;
float perm,aranj,comb,k_fact;
void main()
E7.
Enuntul problemei: Sa se determine daca un numar natural n este perfect (suma divizorilor proprii + 1 este egala cu valoarea numarului). De exemplu, n = 6 este numar perfect deoarece 1 + 2 + 3 = 6.
Metoda de rezolvare: Avem de calculat o suma, deci se poate considera variabila S care se initializeaza cu 0. Apoi, se parcurge multimea divizorilor posibili si daca se gaseste un divizor se adauga la suma anterioara. La final, daca S + 1 = n, atunci n este numar pefect, altfel nu este numar perfect.
Descrierea algoritmului in pseudocod
citeste n *n≥1
S *suma adiv proprii
![]() pentru i = 2,n/2,1 repeta * posibilii divizori proprii
pentru i = 2,n/2,1 repeta * posibilii divizori proprii
![]() daca n%i = 0 atunci * i chiar este divizor al lui n
daca n%i = 0 atunci * i chiar este divizor al lui n
S S + i * il adun la S
![]() daca S+1 = n atunci
daca S+1 = n atunci
scrie "Este numar perfect"
altfel
scrie "Nu este numar perfect"
Descrierea algoritmului in C++:
# include <iostream.h>
# include <conio.h>
void main()
Tema (C4) - termen doua saptamani (maxim)
Scrieti
in pseudocod (eventual si in C/C++) algoritmul pentru calculul sumei
S = 1·3 + 2·4+.+n(n+2), pentru n≥1.
Scrieti
in pseudocod (eventual si in C/C++) algoritmul pentru calculul sumei
S = ![]() , pentru n≥1.
, pentru n≥1.
Scrieti in pseudocod (eventual si in C/C++) algoritmul pentru a stabili daca un numar intreg n≥1 dat este deficient (suma divizorilor proprii+1 < n) sau abundent (suma divizorilor proprii+1 > n). De exemplu, n=12 este abundent deoarece 1+2+3+4+6=16>12, iar n=14 este deficient deoarece 1+2+7<14.
Scrieti in pseudocod (eventual si in C/C++) algoritmul pentru a stabili daca doua numere intregi sunt prietene (1+suma divizorilor proprii ai unuia = celalalt). De exemplu 220 si 284 sunt prietene, deoarece sd(220) = 1 + (2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110) = 284 si sd(284) = 1 + (2 + 4 + 71 + 142) = 220.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |