
Universitatea "Petru Maior" Targu Mures
Facultatea de Stiinte si Litere
Specializarea Matematica - Informatica
LUCRARE DE LICENTA
METODA LUI JACOBI PENTRU SISTEMELE LINIARE INFINITE
INTRODUCERE
In aceasta lucrare este prezentata extinderea metodei numerice iterative a lui Jacobi de la sistemele liniare finite la sistemele liniare infinite, dupa cum spune si titlul. Pana acum s-a studiat aceasta metoda doar pentru sistemele liniare finite in ℝn. Pentru a realiza aceasta extindere, se considera in loc de norme in ℝn, norme in spatii de siruri si in loc de norme matriciale in Mn(ℝ), norme pentru matrici infinite. Aceasta metoda reprezinta o noutate si nu apare in literatura de specialitate.
In capitolul 1 se readuc la cunostinta cateva elemente de analiza matematica si analiza functionala, de care avem nevoie pe parcursul celorlalte doua capitole. Amintim de spatiile metrice, spatiile normate, spatiile Banach, pe baza carora se contureaza normele vectoriale, matriciale si cateva proprietati ale spatiilor de siruri.
Capitolul 2 prezinta metoda numerica a lui Jacobi pentru sistemele liniare finite in ℝn , si se mai face referire la normele vectoriale in ℝn, normele matriciale in Mn (ℝ), compatibilitatea si subordonarea celor doua norme.
In capitolul 3 se prezinta extinderea metodei lui Jacobi la sistemele liniare infinite, la spatiile de siruri. Caracterizam mai intai spatiile de siruri, si anume: l1, l2,lp si l∞. Apoi studiem normele vectoriale pe aceste spatii de siruri, normele matriciale pentru matrici infinite, compatibilitatea si subordonarea dintre ele si in final extinderea metodei lui Jacobi la sistemele liniare infinite.
Capitolul 1: Elemente de analiza matematica si analiza functionala
Spatii metrice
Spatiile metrice formeaza o clasa importanta de spatii topologice. Datoram aceasta notiune matematicianului M. Frechet (1878 - 1973) care, introducand notiunea de distanta intre obiecte matematice de acelasi tip, ne permite sa vorbim de distanta nu numai intre doua puncte din plan.
Definitie
Fie X o multime nevida. O functie d: X x X →ℝ cu proprietatile:
(D1) d(x,x) =0, ∀ x∈ X ;
(D2) d(x,y) =d(y,x), ∀ x,y∈ X (simetrie);
(D3) d(x,y) ≤d(x,z) + d(z,y), ∀ x,y,z∈ X (inegalitatea triunghiului)
se numeste semimetrica (sau semidistanta). Daca , in plus, d verifica si
(D4) d(x,y) =0 ⇒x=y, ∀ x,y∈ X, atunci d se numeste metrica (sau distanta)
Observatie
1. Daca in (D3) punem x=y obtinem d(x,x) ≤d(x,z) + d(z,x),
∀ x,z∈ X, de unde d(x,z) ≥0, ∀ x,z∈ X
2. Putem reduce numarul de axiome care caracterizeaza notiunea de semimetrica. Astfel, (D2) si (D3) sunt echivalente cu (D2')
(D2 ): d(x,y) ≤ d(x,z) + d(y,z), ∀ x,y,z∈ X, deci (D1) + (D2) + (D3) ⇔ (D1) + (D2
Evident (D2) + (D3) ⇒ (D2 ). Reciproc, luam in (D2') z=x si obtinem
d(x,y) ≤ d(x,x) + d(y,x) ⇒ d(x,y) ≤ d(y,x)
Daca inversam pe x cu y avem d(y,x) ≤ d(x,y), deci,
d(x,y) d(y,x), adica (D2).
Definitie
O pereche (X, d) unde d: X x X →ℝ este o metrica (semimetrica) se numeste spatiu metric (semimetric). Elementele unui spatiu metric se numesc puncte.
Observatie
1. Daca perechea (X, d) este un spatiu metric si A ⊂ X este o submultime nevida a lui X, atunci perechea (A, d) este un spatiu metric.
2. Pe o multime nevida X pot fi definite mai multe distante, dupa cum vom constata mai jos, deci mai multe structuri de spatiu metric. Atunci, cand nu este pericol de confuzie, spatiu metric (X, d) va fi notat cu X.
In continuare, vom da cateva exemple de spatii metrice:
1. (ℝ, d) este un spatiu metric, unde d: ℝxℝ →ℝ, d (x,y) = |x-y|,
∀ x, y ∈ X este metrica euclidiana.
2. (ℂ, d) este un spatiu metric relativ la metrica euclidiana
d: ℂxℂ → ℝ, d(z1, z2) = |z1-z2|, ∀ z1, z2∈ ℂ
3. (ℝn, d) este un spatiu metric, unde metrica euclidiana
d: ℝn x ℝn → ℝ se defineste astfel: ∀ x= (x1, x2, , xn) ∈ ℝn ,
∀y= (y1, y2, , yn) ∈ ℝn
d(x,y) ![]()
Verificarea proprietatilor (D1), (D2) si (D4) este imediata.
Pentru a verifica (D3) fie x= (x1, x2, , xn), y= (y1, y2, , yn) si
z= (z1, z2, , zn) ∈ ℝn
(D3) ⇔ [![]()
![]()
![]()
Notam
xi - zi = ai si zi - yi
= bi , i=![]() . Atunci, relatia de
mai sus
. Atunci, relatia de
mai sus
devine
[![]()
![]()
![]() ]1/2 ⇔
]1/2 ⇔
⇔ ![]()
![]()
![]()
![]()
![]() ⇔
⇔
⇔ ![]()
![]()
![]() ]1/2 ⇔
]1/2 ⇔
⇔ [![]()
![]()
![]() ]
]
care nu este altceva decat inegalitatea Cauchy - Buniakowski - Schwartz.
Observam ca spatiile metrice (ℝ2, d) si (ℂ, d) cu distantele euclidiene sunt identice.
4. (ℝn, d) este un spatiu metric, unde d: ℝn x ℝn → ℝ
d(x,y) = ![]() , ∀ x= (x1,
x2, , xn) ∈ ℝn , ∀y= (y1,
y2, , yn) ∈ ℝn
, ∀ x= (x1,
x2, , xn) ∈ ℝn , ∀y= (y1,
y2, , yn) ∈ ℝn
este metrica Manhattan (distanta postasului).
5. (ℝn, d) este un spatiu metric relativ la distanta d: ℝn x ℝn → ℝ .
d(x,y)= ![]() , ∀ x= (x1,
x2, , xn) ∈ ℝn , ∀y= (y1,
y2, , yn) ∈ ℝn
, ∀ x= (x1,
x2, , xn) ∈ ℝn , ∀y= (y1,
y2, , yn) ∈ ℝn
6. (ℝn, d) este un spatiu metric unde d: ℝn x ℝn → ℝ
d(x,y) = [![]() ]1/p, ∀
p≥1, p ∈ℝ, ∀x= (x1, x2, , xn)
∈ ℝn ,
]1/p, ∀
p≥1, p ∈ℝ, ∀x= (x1, x2, , xn)
∈ ℝn ,
∀y= (y1, y2, , yn) ∈ ℝn , este metrica Minkowski (1864- 1909).
7. pentru orice multime nevida X, (X,d), este un spatiu metric, unde
d: X x X→ ℝ,
d(x,y)=![]()
![]() ∀ x,y ∈ X, este metrica discreta.
∀ x,y ∈ X, este metrica discreta.
Un astfel de spatiu metric se numeste spatiu metric discret.
8. Hipercubul de dimensiune n.
Fie B= codul binar. Multimea Bn=BxBx.xB se numeste hipercub de dimensiune n. Orice n-uplu x∈Bn , x= (x1, x2, , xn)= x1x2xn reprezinta un cuvant de cod de lungime n. Definim adunarea modulo 2 in B si o extindem la elementele din Bn . Astfel,∀ x,y∈Bn , x= (x1, x2, , xn) ,
y= (y1, y2, , yn),
x⊕y=( x1⊕y1, xn⊕yn).
Pentru ,∀ x,y∈Bn se defineste d(x,y)=![]() , adica numarul de componente ale lui x si y care
nu coincid.
, adica numarul de componente ale lui x si y care
nu coincid.
Se verifica usor ca (Bn, d) este un spatiu metric d, unde d se numeste distanta Hamming (1915-1998).
Hipercubul de dimensiune 2 este patratul avand latura de lungime 1 si ca varfuri cuvintele de cod 00, 01, 10, 11. Hipercubul de dimensiune 3 este cubul obijnuit de latura avand lungimea 1, iar ca varfuri cuvintele de cod 000, 001, 010, 100, 011, 101, 110, 111.
Multimea Bn are o interpretare remarcabila si
anume Bn ≃An , unde An este
multimea de numere naturale . Orice
numar x∈An are o reprezentare unica de forma x=![]() cu ai∈B si
poate fi astfel identificat cu punctul a1a2 an∈Bn.
cu ai∈B si
poate fi astfel identificat cu punctul a1a2 an∈Bn.
9. Fie A o multime nevida, A ∈ℝn.
(M(A), d) este un spatiu metric unde M(A) este multimea functiilor numerice, reale, marginite definite pe A, iar d: M(A)x M(A) →ℝ definita prin
d(f,g)= supx∈A|f(x)-g(x)|, ∀ f,g ∈ M(A) este distanta uniforma. Verificarea conditiilor (D1), (D2) si (D4) este imediata. Aratam ca are loc si conditia (D3). Avem inegalitatile evidente ∀f,g,h ∈ M(A), ∀x∈A
|f(x)-g(x)|≤ |f(x)-h(x)| + |h(x)-g(x)|≤ supx∈A|f(x)-h(x)| + supx∈A|h(x)-g(x)|.
Atunci
supx∈A|f(x)-g(x)|≤ supx∈A|f(x)-h(x)| + supx∈A|h(x)-g(x)|,
adica d(f,g)≤ d(f,h) + d(h,g), ∀f,g,h ∈ M(A).
10. (Ck([a,b]),d) este spatiul metric, unde
Ck([a,b])=, iar
d: Ck([a,b])x
Ck([a,b]) →ℝ este definita prin d(f,g)=![]() |f(n)(x)- g(n)(x)|, metrica
Cebasev (1821-1894).
|f(n)(x)- g(n)(x)|, metrica
Cebasev (1821-1894).
1.1.9. Definitie
Fie (X,d) un spatiu metric. Spunem ca un sir de elemente din ℝn converge la x∈ ℝn, daca sirul de numere reale converge la 0, deci daca ∀ℇ> 0, ∃ nℇ∈ℝ* astfel incat d(xn, x)<ℇ , ∀n≥ nℇ . Vom folosi notatia
xn
→x sau ![]() .
.
Exemple:
1.Daca X= si d(x,y)=|x-y|, atunci converge la x daca ∀ℇ> 0,
∃ nℇ∈ℝ* astfel incat |xn- x|<ℇ , ∀n≥ nℇ.
Regasim astfel definitia cunoscuta a sirului de numere reale convergent.
2. Fie X= ℝn , si fie
, un sir de elemente (vectori) din ℝn. Fiecare
element xk va fi de forma xk=(xk1,xk2,xkn), xki∈γ, ∀![]() . Daca
. Daca
x= (x1, x2,
, xn), atunci xk![]() x daca ∀ℇ>
0, ∃ nℇ∈ℝ* astfel incat
x daca ∀ℇ>
0, ∃ nℇ∈ℝ* astfel incat
d(xk, x)<ℇ
, ∀n≥ nℇ . Tinand seama de definitia
distantei ℝn aceasta revine la: | xki-xi|
< ℇ, ∀k≥ nℇ, ∀![]() .
.
Astfel, am obtinut urmatorul rezultat
1.1.10. Teorema
Sirul de numere converge in ℝn la
elementul x, daca si numai daca xki converge in γ
la xi ,∀![]() .
.
In concluzie, convergenta unui sir de elemente (vectori) din ℝn, revine la convergenta pe componente.
De exemplu, sirul → (1,0) in ℝ2.
3. Fie X=ℂ si d(z1,z2)=|z1-z2| , ∀z1,z2∈ℂ.
1.1.11. Teorema
Un sir de numere complexe , unde pentru ∀n, zn=xn+iyn, converge in ℂ la z=x+iy, daca si numai daca xn→x si yn→y in γ.
Demonstratie
zn→z in ℂ
daca si numai daca ![]() .
.
Din inegalitatile evidente:
max≤![]() |xn-x|+ |yn-y| , rezulta
ca zn→z in ℂ
daca si numai daca xn→x si yn→y
in γ.
|xn-x|+ |yn-y| , rezulta
ca zn→z in ℂ
daca si numai daca xn→x si yn→y
in γ.
4. Fie X=B(E) multimea functiilor reale si marginite pe E. Un sir de functii converge la f in B(E) daca ∀ℇ> 0, ∃ nℇ∈ℕ* astfel incat:
d(fn,f) =![]()
![]() < ℇ, ∀n≥ nℇ.
< ℇ, ∀n≥ nℇ.
Aceasta definitie este echivalenta cu urmatoarea:
∀ℇ> 0, ∃ nℇ∈ℕ* astfel incat |fn(x)-f(x)| < ℇ, ∀n≥ nℇ, si ∀ x∈E.
1.1.12 Teorema
Un sir de
functii converge la f in B(E) daca si numai daca![]() .
.
1.1.13 Definitie
Un sir de elemente dintr-un spatiu metric X se numeste fundamental (Cauchy) daca ∀ℇ> 0, ∃ nℇ∈ℕ* astfel incat d(xn,xm)< ℇ,
∀n,m≥ nℇ.
Daca X= γ si d(x,y)=|x-y|, reobtinem definitia sirului fundamental de numere reale.
1.1.14 Definitie
Un sir se numeste marginit daca ∃ a∈X si r>0, astfel incat d(xn,a)<r, ∀ n∈ℕ . Principalele proprietati ale sirurilor de elemente dintr-un spatiu metric sunt concentrate in urmatoarea teorema:
1.1.15 Teorema
Fie (X,d) spatiu metric.
i) Daca xn![]() x si yn
x si yn![]() y atunci
y atunci ![]() d(xn,yn)=d(x,y);
d(xn,yn)=d(x,y);
ii) Orice sir convergent are limita unica;
iii) Orice sir convergent este fundamental;
iv) Orice sir fundamental este marginit;
v) Orice subsir al unui sir convergent este convergent si are limita egala cu limita sirului initial.
Demonstratie
i) Stim ca | d(xn,yn) - d(x,y) | < d(xn,x) + d(yn,y).
Cum ![]() d(xn,x)=
d(xn,x)= ![]() d(yn,y)=0, rezulta ca
d(yn,y)=0, rezulta ca ![]() d(xn,yn)=
d(xn,yn)=
![]() d(x,y).
d(x,y).
ii) Presupunem ca ![]() si de
asemenea
si de
asemenea ![]() . Din i) rezulta d(x,y)=
. Din i) rezulta d(x,y)= ![]() , deci y=x.
, deci y=x.
iii) Daca xn![]() x , atunci ∀ℇ> 0, ∃ nℇ∈ℕ*
astfel incat d(xn,x)< ℇ/2,
x , atunci ∀ℇ> 0, ∃ nℇ∈ℕ*
astfel incat d(xn,x)< ℇ/2,
∀n≥ nℇ. Pentru ∀ m> nℇ avem de asemenea d(xm,x)<
Din proprietatea a III-a a distantei rezulta
d(xn,xm)≤ d(xn,x)+ d(x,xm)< ℇ/2+ ℇ/2= ℇ, m,n> nℇ;
deci este fundamental.
iv) Fie un sir fundamental si ℇ = 1. Atunci, ∃ n1∈ℕ*, astfel incat d(xn,xm)<1, ∀ m,n≥n1. In particular, d(xn1,xm)<1, m>n1.
Fie α = max si fie r=max. Evident, d(xn1,xm)<r, ∀ m∈ℕ*, deci este marginit.
v) Fie xn![]() x. Orice subsir al
sirului este la randul sau un sir de forma ,
unde k1<k2<.<kn<. este un sir
strict crescator de numere naturale.
x. Orice subsir al
sirului este la randul sau un sir de forma ,
unde k1<k2<.<kn<. este un sir
strict crescator de numere naturale.
Pentru ℇ> 0, ∃ nℇ∈ℕ* astfel incat d(xn,x)< ℇ, ∀n≥ nℇ. Deoarece kn≥n, rezulta d(xkn,x)< ℇ, ∀n≥ nℇ, deci xkn→x.
Am vazut ca orice sir convergent este fundamental. Afirmatia reciproca nu este in general adevarata. Exista spatii metrice care contin siruri fundamentale divergente.
Exemplu
Fie X=ℕ si
d(x,y)=|x-y|, ∀x,y∈ℕ. Consideram
sirul xn=![]() . Acest sir este fundamental in γ, dar nu
este convergent in ℕ deoarece
. Acest sir este fundamental in γ, dar nu
este convergent in ℕ deoarece
![]() ∉ ℕ.
∉ ℕ.
1.2. Spatii normate
1.2.1. Definitie
Fie X o multime si functiile +:X x X→ X si functia ∗:K x X→ X cu urmatoarele proprietati:
sv1) x+(y+z)=(x+y)+z, ∀x,y,z∈X;
sv2) ∃ 0x∈X astfel incat x+0x=x, ∀x∈X;
sv3) 1∗x=x, ∀x∈X;
sv4) ∗x)= ( )∗x, ∀ ∈K, ∀x∈X;
sv5) (x+y)= x+ y, ∀ ∈K, ∀x,y∈X;
sv6) ( )x= x+ x, , ∀ ∈K, , ∀x∈X.
(X,+.∗) se numeste spatiu vectorial peste K. (X/K)
1.2.2. Observatie
1) x+y=y+x, ∀x,y∈X folosind sv3), sv5) si sv6);
2) ∀x∈X, ∃ x'∈X astfel incat x'+x=0x
0x=(1+(-1))∗x=1∗x+(-1)*x=x+(-1)*x
x'=(-1)*x=-x
Exemple:
kn=
x+y= (x1+y1,
x2+y2 , xn+yn ) 0kn= ![]()
αx=(αx1, αx2, , αxn)
(kn, +,*) spatiu vectorial peste K
s=
x=(xn)n∈ℕ, y∈(yn)n∈ℕ,
+: s x s → s
x+y= (xn+yn)n∈ℕ
*: k x s → s, ∀α∈K
α*x=(αxn) n∈ℕ
0s=(0,0,0,)
(s,+,*) spatiu vectorial peste K
Fie X spatiu vectorial peste K si I nevida
XI
+:XI x XI → XI
x,y∈ XI
(x+y)(i)=x(i)+y(i), ∀ i∈I
∈K
*:K x XI → XI
*x)(i)= *x(i), ∀i∈I
(XI, +, *) spatiu vectorial peste K.
In definitia spatiului metric nu s-a presupus ca multimea X are vreo structura algebrica. Din aceasta cauza, intr-un spatiu metric oarecare nu se poate dezvolta o teorie a seriilor, deoarece nu are sens operatia de adunare. Pentru a elimina aceasta deficienta vom introduce notiunea de spatiu normat, in care se presupune ca multimea X este un spatiu vectorial.
Definitie
Fie X un spatiu vectorial peste corpul K Se numeste norma pe X orice
aplicatie || || : X → ℝ cu proprietatile:
(i) ||x||≥0, ∀ x∈X, si ||x||=0 daca si numai daca x=0x
(ii) ||λx||=|λ| ||x||, ∀λ∈K, ∀x∈X
(iii) ||x+y||≤||x|| + ||y||, ∀x,y∈X
Perechea (X,|| ||) se numeste spatiu normat.
Exemple
Multimea este un spatiu normat in raport cu norma
||x|| = |x|, ∀x∈
Multimea ℝn este un spatiu normat in raport cu norma
||x||∞ =max , unde x= (x1, x2, , xn)∈ ℝn este un vector oarecare.
Multimea numerelor complexe este un spatiu normat in raport cu norma
||z|| = |z| = ![]() , ∀z=x+iy ∈ ℂ.
, ∀z=x+iy ∈ ℂ.
Multimea B(E) a functiilor reale si marginite pe E este un spatiu normat in raport cu norma
||f||∞ = sup.
Observatie
Orice spatiu normat este un spatiu metric in raport cu distanta
d(x,y)=||x-y||, ∀x,y∈X.
Afirmatia reciproca nu este in general adevarata. Exista si spatii metrice care nu sunt spatii normate.
Exemplu
Fie A o multime oarecare si fie X=.
Evident X este un spatiu metric in raport cu distanta:
d(f,g)=sup.
Observam insa ca X nu este spatiu normat deoarece nu este spatiu vectorial.
Intr-adevar, daca f,g∈X si α,β∈γ, atunci αf+ βg in general nu apartine lui X.
Cum spatiile normate sunt cazuri particulare de spatii metrice, rezulta ca definitiile si rezultatele privind sirurile in spatii metrice raman valabile si in spatii normate. Astfel, daca X este un spatiu normat, atunci un sir de elemente din X converge la elementul x∈X, daca si numai daca:
![]() .
.
1.3 Teorema de punct fix a lui Banach
1.3.1 Definitie
Un spatiu metric (X,d) se numeste complet daca orice sir fundamental de elemente din X este convergent catre un element din X. Din criteriul general de convergenta a lui Cauchy pentru siruri de numere reale rezula ca γ este un spatiu metric complet in raport cu distanta euclidiana
d(x,y) = |x-y|, ∀x,y∈ γ.
Teorema
Spatiul ℝn este complet.
Demonstratie
Fie un sir de elemente din ℝn . Fiecare element xk este de forma
xk= (xk1, xk2, , xkn)
Din inegalitati evidente:
|xki-xli|
≤ ![]() , rezulta ca in
demonstratia teoremei 1.1.10 ca este fundamental in ℝn
daca si numai
daca este
fundamental in γ,
, rezulta ca in
demonstratia teoremei 1.1.10 ca este fundamental in ℝn
daca si numai
daca este
fundamental in γ, ![]() . Afirmatia din teorema rezulta acum din
criteriul general de convergenta a lui Cauchy pentru siruri de
numere reale si din teorema 1.1.10. Intr-adevar , daca
este fundamental in ℝn atunci este fundamental in γ, deci convergent pentru
. Afirmatia din teorema rezulta acum din
criteriul general de convergenta a lui Cauchy pentru siruri de
numere reale si din teorema 1.1.10. Intr-adevar , daca
este fundamental in ℝn atunci este fundamental in γ, deci convergent pentru ![]() . Din teorema 1.1.10 rezulta
. Din teorema 1.1.10 rezulta
convergent in ℝn .
Teorema
Spatiul numerelor complexe ℂ este complet.
Demonstratie
Daca zn=xn+iyn, atunci conform teoremei 1.1.11 zn→z=x+iy daca si numai daca xn→x si yn→y in γ. In mod analog se arata ca este fundamental daca si numai daca si sunt fundamentale in γ. Afirmatia rezulta acum (ca si in teorema 1.3.2) din criteriul general de convergenta a lui Cauchy pentru siruri de numere reale.
Teorema
Spatiul B(E) al functiilor reale si marginite pe E este complet.
Demonstratie
Din teorema 1.1.12 rezulta ca converge la f in B(E) daca si numai daca ![]() .
.
Definitie
Fie (X,d) un spatiu metric. Se numeste contractie pe X orice aplicatie
T : X → X cu proprietatea ca exista 0≤α<1 astfel incat
d(T(x),T(y)) ≤ αd(x,y), ∀x,y∈X.
Teorema Banach
Daca (X,d) este un spatiu metric complet si T : X → X este o contractie, atunci exista z∈X, unic, astfel incat T(z)=z.
Demonstratie
Alegem un punct oarecare x0∈X si notam cu
x1=T(x0), x2=T(x1), ., xn=T(xn-1), .
Vom arata ca sirul este fundamental. Intr-adevar,
d(x1,x2)=d(T(x0),T(x1))≤ d(x0,x1)
d(x2,x3)=d(T(x1),T(x2))≤ d(x1,x2) ≤ d(x0,x1).
Prin inductie completa se arata ca
d(xk,xk+1) ≤ kd(x0,x1), ∀k∈ℕ*.
In continuare avem
d(xk,xk+p) ≤ d(xk,xk+1)+ d(xk+1,xk+2)+ + d(xk+p-1,xk+p) ≤
k k+1 k+p-1)d(x0,x1)=![]() d(x0,x1)<
d(x0,x1)<![]() <d(x0,x1),
<d(x0,x1),
∀k,p∈ℕ*. (1.1)
Deoarece 0≤α≤1, avem αk→0, deci ∀ ℇ>0, ∃ kℇ∈ℕ*, astfel incat
k<![]() , ∀k> kℇ.
Rezulta d(xk,xk+p)<ℇ, ∀k> kℇ
si ∀p∈ℕ*, deci este sir
fundamental. Cum X este complet rezulta ca ∃ z∈ X astfel
incat xk→z. Mai departe avem:
, ∀k> kℇ.
Rezulta d(xk,xk+p)<ℇ, ∀k> kℇ
si ∀p∈ℕ*, deci este sir
fundamental. Cum X este complet rezulta ca ∃ z∈ X astfel
incat xk→z. Mai departe avem:
d(z, T(z)) ≤ d(z,xk) + d(xk, T(z))= d(z,xk) + d(T(xk-1, T(z)) ≤
≤ d(z,xk) + α d(xk-1,z).
Deoarece, conform teoremei 1.1.15. punctul i), membrul drept tinde la 0, rezulta d(z, T(z))=0, deci, T(z)=z. Pentru a putea demonstra unicitatea punctului fix z, sa presupunem ca ∃z`∈X astfel incat T(z`)=z`. Atunci avem:
d(z,z`)=d(T(z),T(z`))≤ α d(z,z`).
Cum, 0≤α<1, aceasta ineglitate nu poate avea loc decat daca d(z,z`)=0, adica daca z=z` si cu aceasta teorema este demonstrata.
Sirul , obtinut pornind de la un punct arbitrar x0∈X, prin relatia de recurenta xk=T(xk-1), ∀k∈ℕ*, se numeste sirul aproximatiilor succesive, iar metoda de obtinere a punctului fix z ca limita a acestui sir, poarta numele de metoda aproximatiilor succesive. E. Picard a obtinut metoda aproximatiilor succesive cu mult inainte ca Banach sa fi stabilit rezultatul sau foarte general (Teorema 1.3.6.). Din aceasta cauza, aceasta metoda se mai numeste si metoda Picard - Banach.
Pentru a evalua eroarea in metoda aproximatiilor succesive, trecem la limita dupa p in inegalitatea (1.1) si obtinem:
d(xk,x)≤![]() d(x0,x1) (1.2)
d(x0,x1) (1.2)
Asadar, daca
aproximam pe z cu xk facem o eroare care este mai mica
decat ![]() d(x0,x1).
d(x0,x1).
Teorema 1.3.6. are numeroase aplicatii in matematica. Pentru exemplificare, vom arata cum poate fi folosita metoda aproximatiilor succesive la rezolvarea ecuatiilor algebrice sau transcendente.
Fie ecuatia F(x)=0, x∈[a,b] (1.3)
Aceasta ecuatie se inlocuieste cu ecuatia echivalenta:
x=f(x); x∈[a,b] (1.4)
Acest lucru se poate realiza de exemplu, daca notam f(x)= x+F(x). Sa presupunem ca f: [a,b] →[a,b] este derivbila si exista 0≤α<1 astfel incat
|f`(x)|≤α, ∀ x∈ [a,b]. (1.5)
Din teorema Lagrange rezulta ca ∀ x,y∈ [a,b], ∃ξ intre x si y astfel incat
f(x) - f(y)= f`( )(x-y). Tinand seama de (1.5) obtinem:
|f(x)-f(y)|≤ |x-y|, ∀ x,y∈ [a,b]. (1.6)
Din (1.6) rezulta ca f este o contractie pe [a,b], iar din teorema (1.3.6) rezulta ca exista o solutie unica z a ecuatiei (1.4) care se poate obtine cu metoda aproximatiilor succesive. Din punct de vedere geometric, orice solutie a ecuatiei (1.4) este abscisa unui punct de intersectie din dreapta y=x si graficul functiei y=f(x).
Pe figura (1) se poate urmari sirul aproximatiilor succesive pentru 0<f`(x)≤α<1 , iar pe figura (2), pentru -1<-α≤f`(x)<0.
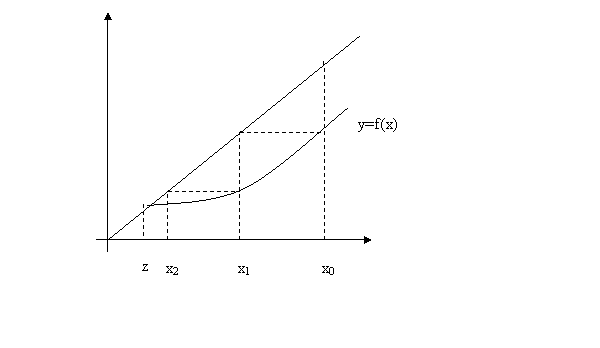
.Figura 1
x0 y=f(x) x2 x3 x1
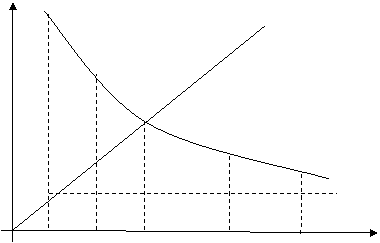
z
Figura 2
Exemplu
Fie ecuatia x5-x-0,2=0, care admite o radacina in intervalul
[-0,3; -0,2]. Ecuatia echivalenta este x=x5-0,2, deci f(x)= x5-0,2.
Se verifica imediat ca |f'(x)|<0,05, ∀x∈[-0,3; -0,2] deci putem lua
Dupa prima aproximatie se poate lua x0=-0,2.
Aflarea unei solutii aproximative se face cu ajutorul calculatorului.
1.4. Spatii Banach
1.4.1. Definitie
Orice spatiu normat si complet se numeste spatiu Banach.
Intre cele mai simple spatii Banach distingem spatiile liniare standard n-dimensionale ℝn si ℂn peste corpul ℝ, respectiv ℂ, normate cu ajutorul normei euclidiene
||z||= (|z1|2 + . + |zn|2 )1/2, z=(z1, . , zn).
In continuare, vom da cateva exemple de spatii Banach pe care le vom demonstra.
1.4.2. Normarea si completitudinea spatiului CB(T).
Fie T un spatiu topologic Hausdorf, T≠∅, se defineste
CB(T)=.
1. CB(T) ⋐ B(T) ne bazam pe adunare si produsul cu scalari. Normam cu norma indusa ||x||= sup. Pentru orice element din B(T), este verificata ca a fi spatiu normat.
Observatie:
T compact Hausdorf. ∀ f:T
→ℝ continua rezulta ca f este marginita
(isi atinge marginile: ∃ t0∈T astfel incat f(t0)=
![]() f(t)).
f(t)).
Daca x: T→K este continua, cu f: T→ℝ atunci f(t)=|x(t)| va fi continua.
||x(t)|- |x(t`)||≤|x(t)- x(t`)|, atunci x este continua , deci rezulta |x(t)- x(t`)|<ℇ rezulta ca f este continua. Prin compunere rezulta ca sup< +∞
(∃t0∈T: |x(t0)|= sup).
Observatie: supremumul daca este atins se noteaza cu max.
Daca T este spatiu topologic Hausdorf, T≠∅, definim
C(T)=.
CB(T) ⋐ C(T).
2. Stiind ca spatiul T este un compact Hausdorf, T≠∅, ⇒
⇒ C(T)=CB(T).
3. CB(T) este un spatiu Banach (urmeaza sa demonstram completitudinea).
B(T) este spatiu Banach, CB(T) ⋐ B(T) si tinand cont ca CB(T) este inchis in B(T) din aceste doua reiese ca CB(T) este un spatiu Banach.
![]()
![]()
x∈![]() ⇒ ∃ (xn)n∈ℕ ∈
CB(T) : xn →x in B(T).
⇒ ∃ (xn)n∈ℕ ∈
CB(T) : xn →x in B(T).
∀ℇ>0 ∃n0∈ℕ astfel incat ∀n≥n0 ||xn-x|| < ℇ.
∀ℇ>0 ∃n0∈ℕ astfel incat ∀t∈T, ∀n≥n0 : |xn(t)-x(t)| < ℇ.
|xn(t)-x(t)| <||xn-x||. (este o convergenta
uniforma ![]() )
)
∀ℇ>0 si ∀t∈T ∃n0∈ℕ, n0= n0(ℇ, t) , ∀n≥n0 : |xn(t)-x(t)| < ℇ, adica xn converge punctual catre x.
Avem un sir de functii continue care converge catre x, deci x este continua..
x este marginita deoarece lucram in B(T).
x este continua: ∀t∈T, ∀ℇ>0, ∃ V∈V (t): ∀t`∈V, |x(t)-x(t`)| < ℇ.
ℇ>0, ∃n0∈ℕ, ∀n≥n0 , ∀t∈T, |xn(t)-x(t)| < ℇ/3.
t0∈T fixat: ∀t∈T, |xn0(t)-x(t)| < ℇ/3.
xn0 este continua rezulta ∃ V∈V (t0), ∀t∈V
t∈V, |x(t)-x(t0)|≤ |x(t)-xn0(t)| + |xn0(t)-xn0(t0)| + |xn0(t0)-x(t0)| < ℇ.
1.4.3 Normarea si completitudinea spatiului B(T)
Definitie:
B(T):=, spatiul functiilor marginite pe T.
x marginita ⇔ sup < ∞.
B(T) este un spatiu vectorial.
x,y ∈ B(T) ![]() x+y ∈B(T)
x+y ∈B(T)
(x+y)(t)= x(t)+ y(t), t∈T (punctual)
Definim aplicatia : || || B(T) →ℝ
||x|| = sup , x∈B(T)
(B(T), || ||) este un spatiu normat.
a) x=0 ⇒ ||x||>0
x=0 ⇔ ∀t∈T, x(t)=0, x≠0 ⇒∃t0∈T :
x(t0)≠0, ||x||≥| x(t0)|>0.
b) ||αx||=|α|*||x||.
c) ||x+y||≤||x||+||y||.
∀t∈T |(x+y)(t)|=|x(t)+y(t)| ≤|x(t)|+|y(t)| ≤||x||+||y||
|x(t)| ≤||x|| si |y(t)| ≤||y||.
Trecand la supremumum ||x+y||≤||x||+||y||.
B(T) este un spatiu Banach. (normat si complet)
Demonstratie
||x||=sup
B(T) este complet daca si numai daca orice sir fundamental este convergent.
(xn)n∈ℕ sir fundamental in B(T):
∀ℇ>0 ∃n0∈ℕ astfel incat ∀n, m≥n0 ||xn-xm|| < ℇ.
a) ∀ℇ>0 ∃n0∈ℕ astfel incat ∀n,m≥n0
![]() < ℇ.
< ℇ.
∀ℇ>0 ∃n0∈ℕ astfel incat ∀n,m≥n0 ∀t∈T |xn(t)-xm(t)| < ℇ. (1.10)
Pentru t∈T (xn(t))n∈ℕ sir fundamental in K rezulta din (1.10)
(xn(t)) convergent pentru t∈T fixat, caci K este complet.
Definim x: T →
K astfel incat x(t) ![]() (1.11)
(1.11)
x∈B(T) ? (x marginita
Fie ℇ=1 ⇒∃n0 ∀t∈T ∀n,m≥n0 |xn(t)-xm(t)| <1
∀t∈T , m≥n0 : |xn0(t)-xm(t)| <1
m→∞ ⇒∀ t∈T, |xn0(t)-x(t)| ≤1
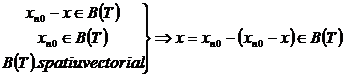
b) x =![]() (in convergenta in B(T)
(in convergenta in B(T)
∀ℇ>0 ∃n0∈ℕ ||xn-x|| < ℇ
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ∀t∈T |xn(t)-x(t)| < ℇ
sirul de functii (xn) converge uniform catre x
Stim ca ∀t∈T , ∀ℇ>0, ∃n0∈ℕ, ∀n≥n0 |xn(t)-x(t)| < ℇ
∀ℇ>0 ∃n0∈ℕ , ∀n,m≥n0 , ∀t∈T :
|xn(t)-xm(t)| <ℇ
pentru n≥n0 fixat si t∈T, m→∞ ⇒ |xn(t)-x(t)| < ℇ.
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ∀t∈T ⇒ |xn(t)-x(t)| < ℇ
pentru n≥n0, ![]() |xn(t)-x(t)| ≤ℇ. ||xn-x|| < ℇ.
|xn(t)-x(t)| ≤ℇ. ||xn-x|| < ℇ.
In continuare vom demonstra ca spatiul sirurilor convergente este un spatiu Banach.
Spatiul l∞ . l∞:=B(ℕ) spatiul sirurilor marginite (spatiu Banach)
1.4.4 Normarea si completitudinea spatiului c.
1) c:= este spatiul sirurilor convergente.
Orice sir
convergent este marginit. c![]() ⋐ l∞
deci c este subspatiu al lui l∞.
⋐ l∞
deci c este subspatiu al lui l∞.
Definim || || : c →ℝ
||x||= sup
2) (c, || ||) normat, este spatiu Banach.
Lema:
Daca (X, S) este spatiu semimetric complet, Y⊆X inchisa ⇒Y completa.
Consecinta:
X spatiu Banach, Y⋐X inchis ⇒ Y spatiu Banach.
Pentru ca c sa fie complet e de ajuns sa aratam ca c este inchis in l∞.
c=![]() c⊂
c⊂![]()
![]() ⊂c ?
⊂c ?
x∈![]() ⇒x∈c
⇒x∈c
x∈![]() ⇔ ∃ (xn)n∈ℕ
⊂c astfel incat lim xn=x (in l∞)
⇔ ∃ (xn)n∈ℕ
⊂c astfel incat lim xn=x (in l∞)
xn= (xni)i∈ℕ ; x=(xi)i∈ℕ
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ||xn-x|| < ℇ.
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ![]() |xni-xi|
<ℇ
|xni-xi|
<ℇ
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , |xni-xi| <ℇ (1.12)
x∈c ⇔ (xi)i∈ℕ este sir fundamental.
∀ℇ>0 ∃i0∈ℕ : ∀i,j≥0 , |xi-xj| <ℇ
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ∀i∈ℕ, |xni-xi| <ℇ/3 (1.13)
Rezulta ca pentru n=n0, ∀i∈ℕ, |xni-xi| <ℇ/3 xn0∈c ⇒ (xi)i∈ℕ este sir fundamental ⇒∃i0∈ℕ : ∀i,j∈ℕ , i,j≥i0 : |xn0i-xn0j| <ℇ/3
i,j≥i0 |xi-xj|≤|xi-xn0i| + |xn0i-xn0j| + |xn0j-xj| <ℇ (1.14)
Se poate arata ca
xn∈c, n∈ℕ xn=(xni)
![]() (siruri
convergente
(siruri
convergente
daca lim xn=x in l∞
x=(xi)i∈ℕ
rezulta ca x∈c si ![]()
x1 x1 x12 . x1i →![]()
x2 x2 x22 . x2i →![]()
x x x2 . xi → ![]()
teorema de inversare la limita
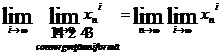
1.4.5 Normarea si completitudinea spatiului c0
c0 = este spatiul sirurilor convergente la 0.
Pentru x=(xi)i∈ℕ ∈c0 ||x||=sup
(se poate arata ca ||x||=max
∃ i0∈ℕ astfel incat ∀i∈ℕ |xi|≤|xi0|
c0⋐c⋐ l∞
c0 este spatiu Banach
c0⋐ l∞ c0 inchis c0=![]()
![]() ⊂c0 ? x∈
⊂c0 ? x∈![]() → x∈ c0 ?
→ x∈ c0 ?
x∈![]() ⇒∃ (xn)n∈ℕ
⊂ c0
⇒∃ (xn)n∈ℕ
⊂ c0 ![]()
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ||xn-x|| <ℇ
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ∀i∈ℕ, |xni-xi| <ℇ
x∈c0 ⇔ ∀ℇ>0 ∃i0∈ℕ ∀i≥i0 , |xi| <ℇ
∀ℇ>0 ∃n0∈ℕ ∀n≥n0 , ∀i∈ℕ, |xni-xi| <ℇ/2
n=n0 ⇒ ∀i∈ℕ, |xn0i-xi| <ℇ/2 (1.15)
(xn0) ∈c0 ⇒ ∃i0∈ℕ ∀i≥i0 , |x n0i| <ℇ/2 (1.16)
Din (1.15) si (1.16) rezulta ca ∀i≥i0 , |x i| ≤|xni-xi| + |x n0i| <ℇ
Capitolul 2: Metoda lui Jacobi pentru sistemele liniare finite in ℝn
2.1. Norme vectoriale in ℝn
Consideram spatiul ℝn si orice norma definita pe acest spatiu o vom denumi norma vectoriala. Sa reamintim axiomele normei: norma || || : ℝn →ℝ este o functie care verifica urmatoarele axiome:
1. ||x+y||≤ ||x|| + ||y|| pentru orice x,y ∈ ℝn
2. ||αx||= |α| ||x|| pentru orice α ∈ ℝ si orice x ∈ ℝn
3. ||x||≥0 pentru orice x ∈ ℝn si ||x||=0 daca si numai daca x=θℝn
In continuare dam exemple de norme vectoriale:
1. Norma euclidiana: ||x||2=![]() , unde x=(x1, x2,
., xn) ∈ ℝn
, unde x=(x1, x2,
., xn) ∈ ℝn
2. Norma maximum: ||x||∞= max , unde
x=(x1, x2, ., xn) ∈ ℝn
3. Norma octaedrica: ||x||1=
![]() , unde x=(x1, x2,
., xn) ∈ ℝn
, unde x=(x1, x2,
., xn) ∈ ℝn
O generalizare naturala a acestor norme ar fi norma data de formula :
||x||p= ![]() , unde p∈[1, +∞)
, unde p∈[1, +∞)
este un numar real fixat sau simbolul +∞, iar x=(x1, x2, ., xn) ∈ ℝn.
In cazul p +∞ dam urmatoarea interpretare:
||x||∞=![]() = max
= max
Mentionam faptul ca, pe spatiul ℝn oricare doua norme vectoriale sunt compatibile, adica oricare ar fi o norma vectoriala || || pe ℝn exista constantele c1, c2 >0 astfel incat c1||x||2≤||x||≤c2||x||2, pentru orice x∈ ℝn.
2.2. Norme matriciale in Mmxn (ℝ).
Consideram spatiul liniar al matricilor cu elemente numere reale avand m lini si n coloane, notat cu Mmxn (ℝ).
2.2.1 Definitie
O norma, || ||: Mmxn (ℝ) →ℝ definita pe spatiul liniar Mmxn (ℝ) o vom numi norma matriciala si se defineste cu aceleasi axiome:
1. ||A+B||≤||A|| + ||B||, pentru orice A,B ∈ Mmxn (ℝ)
2. ||αA||=|α| ||A||, pentru orice α∈ℝ si orice A∈ Mmxn (ℝ)
3. ||A||≥0, pentru orice A ∈ Mmxn (ℝ) si ||A||=0 daca si numai daca A=Omxn, unde cu Omxn am notat matricea nula cu m lini si n coloane.
Un exemplu de norma matriciala ar fi:
||A||= 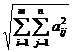 , unde A=
, unde A=![]() ∈ Mmxn (ℝ).
∈ Mmxn (ℝ).
Daca m=n atunci avem matricile patratice de ordinul n cu numere reale, notate simplu cu Mn (ℝ) in loc de Mnxn (ℝ). In acest caz mai adaugam si urmatoarea axioma la axiomele normei matriciale:
4. ||A·B||≤||A||·||B|| pentru orice A,B ∈ Mn (ℝ)
Exemple de norme matriciale pentru matrici patratice
Norma Frobenius
definita de relatia ||A||F
= 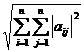 , este o norma matriciala.
, este o norma matriciala.
Vom arata ca aceasta norma satisface conditiile din definita normei matriciale.
Introducem notatiile:
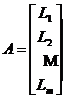 = [C1 C2.Cn] in care
= [C1 C2.Cn] in care
Li = (ai1
ai2 . ain)∈ℂn, i=1, ., n; Cj
= ![]() ∈ℂm,
j=1, ., n.
∈ℂm,
j=1, ., n.
Cu aceste notatii vom avea:
||A||F = 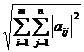
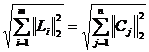
Din definitie rezulta ca:
(1) ||A||F ≥0 ⇔∀i=1,.m, ∀j=1,.n, aij = 0 ⇔A = 0.
(2) Fie A = (![]() ) ∈ℂmxn
si B=(
) ∈ℂmxn
si B=(![]() ∈ℂmxn
∈ℂmxn
![]()
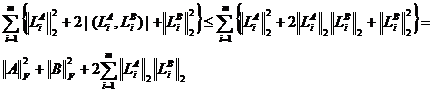
Consideram vectorii:
a = (![]() ) ∈ℂm si b
) ∈ℂm si b ![]() ) ∈ℂm
. Atunci produsul scalar in ℂm
) ∈ℂm
. Atunci produsul scalar in ℂm ![]() . Din aceste
relatii rezulta
. Din aceste
relatii rezulta
![]() .
.
Deci ![]() .
.
(3) Fie ∈ ℂ si A ∈ ℂmxn . Avem
![]()
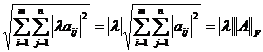
(4) Fie matricile A ∈ℂmxn si B ∈ℂmxn
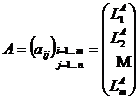 ,
, ![]() ℂn, - linia i a matricii A
ℂn, - linia i a matricii A
![]() ℂn
- coloana j a matricii B.
ℂn
- coloana j a matricii B.
Matricea produs M=A*B ∈ ℂmxp are elementele
![]() .
.
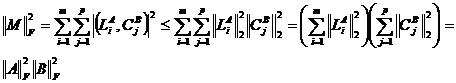
Am aratat ca aplicatia Frobenius este o norma matriciala.
Aplicatia ||A||max = max nu este o norma matriciala.
Pentru n=2 fie
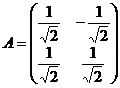
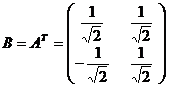
A*B
= I2, ||A||max
=||B||max = ![]()
||A*B||max
=1 > ||A||max ·||B||max =![]()
2.2.2 Norme matriciale naturale
Fie ||·||v : ℝn → ℝ o norma vectoriala. Pornind de la aceasta norma vectoriala definim o norma matriciala numita norma matriciala naturala sau indusa.
![]()
= max
= max
||A||i se numeste norma matriciala naturala sau norma indusa de norma vectoriala ||·||v .
Avem urmatoarea relatie:
||Ax||v≤ ||A||i||x||v , ∀A∈ ℝnxn, ∀x∈ ℝn .
Norma Frobenius ||·||F nu este o norma naturala. Intr-adevar, pentru orice norma vectoriala ||·||v , norma matriciala indusa a matricii unitate este 1:
![]()
iar in cazul normei Frobenius avem :
||In||F
= (1+1+.+1)1/2 = ![]() ≠1 pentru n≥2.
≠1 pentru n≥2.
Pentru ||x||1 = ![]() norma matriciala indusa este:
norma matriciala indusa este:
||A||1 = max
Pentru ||x||∞ = max norma matriciala indusa este:
||A||∞ = max.
Daca ||·||v este o norma vectoriala si P∈ ℝnxn este o matrice nesingulara atunci aplicatia ||·||P: ℝn→ ℝ , ||x||p = ||Px||v este deasemenea o norma vectoriala. Consideram normele matriciale induse de ||·||v si ||·||P - ||·||i si respectiv ||·||i,P . Legatura dintre cele doua norme matriciale este data de relatia ||A||i,P= ||PAP-1||i .
2.3. Compatibilitatea normelor vectoriale cu cele matriciale in ℝn
2.3.1 Definitie
O norma matriciala pe spatiul liniar Mn (ℝ) se numeste compatibila cu o norma vectoriala pe spatiul ℝn daca are loc inegalitatea ||A·x||≤ ||A||·||x|| pentru orice matrice A∈ Mn (ℝ) si orice vector x∈ℝn .
Se verifica usor ca
norma matriciala ||A||=![]() , unde
, unde
A=![]() ∈ Mn (ℝ),
este compatibila cu norma vectoriala euclidiana ||x||2=
∈ Mn (ℝ),
este compatibila cu norma vectoriala euclidiana ||x||2=![]() , unde x=(x1, x2,
., xn) ∈ ℝn
, unde x=(x1, x2,
., xn) ∈ ℝn
Mentionam faptul ca inegalitatea ||A·x||≤||A||·||x|| exprima continuitatea aplicatiilor liniare definite pe spatiul ℝn reprezentate prin matricile A.
2.4. Norme matriciale subordonate normelor vectoriale in ℝn
2.4.1 Definitie
Dintre toate normele matriciale compatibile cu o norma vectoriala sa alegem pe cea mai mica, data de formula
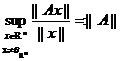
In acest fel se defineste o norma. Tot la fel se demonstreaza ca
![]() .
.
Aceasta norma matriciala o vom denumi norma matriciala subordonata normei vectoriale.
In continuare prezentam normele matriciale subordonate diferitelor norme vectoriale:
1. pentru norma vectoriala
euclidiana avem norma matriciala subordonata data de
formula: ||A||2 = ![]() unde este cea mai mare
valoare proprie a matricii A*A, unde A* este matricea adjuncta a matricii
A. Mentionam ca toate valorile proprii ale lui A*A sunt
pozitive, iar matricea adjuncta A* se obtine din matricea A printr-o
transpunere in cazul real.
unde este cea mai mare
valoare proprie a matricii A*A, unde A* este matricea adjuncta a matricii
A. Mentionam ca toate valorile proprii ale lui A*A sunt
pozitive, iar matricea adjuncta A* se obtine din matricea A printr-o
transpunere in cazul real.
2. pentru norma vectoriala maximum avem norma matriciala linie data de formula :
||A||∞
= ![]() .
.
3. pentru norma vectoriala octaedrica avem norma matriciala coloana data de formula:
||A||1
= ![]() .
.
2.5. Perturbatii
Fie dat sistemul liniar sub forma matriciala A·x = b, unde
A=![]() ∈ Mn (ℝ), x=(x1,
x2, ., xn)T ∈ ℝn, b=(b1, b2, ., bn)T
∈ ℝn. Presupunem ca avem un sistem de tip Cramer cu
det A≠0. Totodata presupunem ca datele de intrare: elementele
matricii A si elementele termenului liber b sufera mici perturbatii, si am astepta ca
si la datele de iesire x
sa obtinem perturbatii de acelasi ordin. Insa acest
lucru nu se adevereste, si ne vom exprima sub forma: sistemul liniar
este instabil din punct de vedere numeric, daca numarul de
conditionare ℋ(A)=||A|| ·||A-1|| este "mare", de ordinul 105,
106, .
∈ Mn (ℝ), x=(x1,
x2, ., xn)T ∈ ℝn, b=(b1, b2, ., bn)T
∈ ℝn. Presupunem ca avem un sistem de tip Cramer cu
det A≠0. Totodata presupunem ca datele de intrare: elementele
matricii A si elementele termenului liber b sufera mici perturbatii, si am astepta ca
si la datele de iesire x
sa obtinem perturbatii de acelasi ordin. Insa acest
lucru nu se adevereste, si ne vom exprima sub forma: sistemul liniar
este instabil din punct de vedere numeric, daca numarul de
conditionare ℋ(A)=||A|| ·||A-1|| este "mare", de ordinul 105,
106, .
Presupunem prima data ca termenul liber b sufera mici perturbatii, iar matricea A ramane neschimbata. Variatia termenului liber b, notata cu δb, induce o variatie a solutiei x, notata cu δx: A·(x + δx) = b + δb, de unde rezulta Ax + Aδx = b + δb, deci A·δx = δb, adica δx = A-1·δb. Prin urmare:
||δx|| = ||A-1·δb|| ≤ ||A-1||·||δb||. Asadar,
![]() .
.
Insa, ||A||·||x||≥||A·x|| = ||b||, deci
![]() .
.
Prin urmare daca numarul de conditionare este "mic" de ordinul 10-1, 100, 101, atunci o perturbatie mica a termenului liber δb, va implica conform inegalitatii anterioare o perturbatie mica a solutiei δx.
Insa, daca numarul de conditionare ℋ(A)=||A|| ·||A-1|| este mare, de ordinul 105, 106, , atunci se poate intampla ca la o variatie mica a termenului liber δb, de exemplu de ordinul 10-2 , sa obtinem o variatie a solutiei δx de ordinul 10-2·105 = 103. Prin urmare, daca numarul de conditionare este "mic" atunci sistemul liniar este stabil din punct de vedere numeric, iar daca numarul de conditionare este "mare", atunci sistemul liniar poate sa fie instabil din punct de vedere numeric.
De aceasta data presupunem ca elementele matricii A sufera mici perturbatii, notate cu δA, iar termenul liber ramane neschimbat. Obtinem o perturbatie a solutiei x notata cu δx: (A+ δA)(x+ δx) = b, adica
A·x + δA·x + A·δx + δA·δx = b, deci A·δx = -δA(x+δx). Prin urmare: δx = +A-1· δA·(x+ δx) de unde :
|| δx || = ||-A-1· δA·(x+ δx)|| = ||A-1·δA·(x+ δx)|| ≤
≤ ||A-1||·||δA||·||x+· δx||,
adica,
![]() .
.
Se observa ca si si de aceasta data putem trage aceleasi concluzii ca si la prima presupunere, si anume: daca numarul de conditionare ℋ(A) este "mic", atunci sistemul este stabil din punct de vedere numeric, iar daca numarul de conditionare este "mare", atunci sistemul liniar devine instabil din punct de vedere numeric.
2.6. Metoda numerica a lui Jacobi pentru sistemele liniare finite in ℝn
Se considera sistemul liniar sub forma matriciala A·x b, unde
A=![]() ∈ Mn (ℝ), x=(x1,
x2, ., xn)T ∈ ℝn,
∈ Mn (ℝ), x=(x1,
x2, ., xn)T ∈ ℝn,
b=(b1, b2, ., bn)T ∈ ℝn. Forma algebrica a sistemului liniar este:
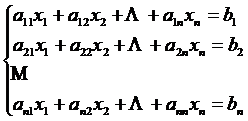
Daca presupunem ca aii≠0 pentru orice ![]() , atunci sistemul liniar se poate pune sub forma
echivalenta, denumita forma iterativa, in felul urmator:
din prima ecuatie se scoate necunoscuta x1, din a doua
necunoscuta x2, , din ultima ecuatie necunoscuta xn,
si se obtine:
, atunci sistemul liniar se poate pune sub forma
echivalenta, denumita forma iterativa, in felul urmator:
din prima ecuatie se scoate necunoscuta x1, din a doua
necunoscuta x2, , din ultima ecuatie necunoscuta xn,
si se obtine:
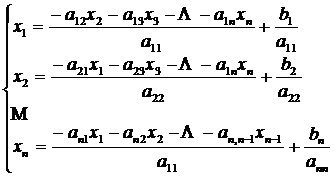
Transcriem sistemul iterativ sub forma matriciala:
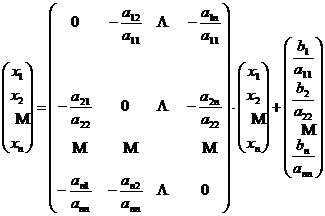 .
.
Introducem notatiile:
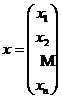 ,
,  si
si 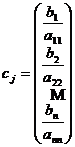 .
.
Astfel sistemul initial apare sub forma matriciala iterativa echivalenta: x=Bj·x + cj. Alegem un punct initial de pornire x=(x01, x02, ., x0n) ∈ ℝn si incepem sa iteram sirul (xk)k∈ℕ⊂ℝn in felul urmator:
x1=Bj·x0 + cj, x2=Bj·x1 + cj, , xk+1=Bj·xk + cj,
Iteratia xk+1=Bj·xk + cj scrisa pe larg inseamna:
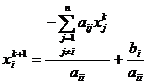
ceea ce este echivalent cu
![]()
pentru orice ![]() . Astfel putem determina matricile Bj si cj
in functie de datele initiale: matricile A si b.
Intr-adevar, fie A=L+D+U descompunerea matricii A in matricea strict
inferior triunghiulara L, matricea diagonala D si matricea
strict superior triunghiulara U. Mentionam ca matricile L,
D, U sunt matrici patratice de ordinul n, unde elementele nealese din
matricea A sunt egale cu zero. Prin urmare: L·xk + D·xk+1
+ U·xk = b, adica:
. Astfel putem determina matricile Bj si cj
in functie de datele initiale: matricile A si b.
Intr-adevar, fie A=L+D+U descompunerea matricii A in matricea strict
inferior triunghiulara L, matricea diagonala D si matricea
strict superior triunghiulara U. Mentionam ca matricile L,
D, U sunt matrici patratice de ordinul n, unde elementele nealese din
matricea A sunt egale cu zero. Prin urmare: L·xk + D·xk+1
+ U·xk = b, adica:
xk+1 = -D-1(L+U)·xk
+ D-1b, ceea ce inseamna ca Bj = -D-1(L+U)
si cj=D-1b. Deoarece conform presupunerii aii≠0
pentru orice ![]() rezulta ca
exista matricea inversa D-1, caci det(D)=
rezulta ca
exista matricea inversa D-1, caci det(D)=![]()
Mentionam urmatorul rezultat referitor la convergenta sirului (xk)k∈ℕ ca o conditie suficienta:
2.6.1 Propozitie
Daca matricea A este dominant
diagonala, adica 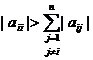 pentru orice
pentru orice ![]() , atunci sirul iterativ (xk)k∈ℕ⊂ℝn
generat mai sus va fi convergent pentru orice punct initial de pornire x0∈ℝn
.
, atunci sirul iterativ (xk)k∈ℕ⊂ℝn
generat mai sus va fi convergent pentru orice punct initial de pornire x0∈ℝn
.
Demonstratie: Sa alegem pe ℝn norma vectoriala maximum:
||x||∞
= max si norma matriciala subordonata, numita
norma linie, data de formula ||Bj||∞
= ![]() , unde B=
, unde B=![]() . Pentru orice
. Pentru orice ![]() conditia
conditia 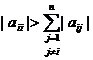 este echivalenta
cu
este echivalenta
cu 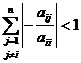 , adica suma elementelor in modul in linia i din
matricea Bj este strict mai mica decat unu. Prin urmare
, adica suma elementelor in modul in linia i din
matricea Bj este strict mai mica decat unu. Prin urmare
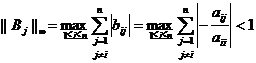 .
.
Astfel, daca notam cu Φ: ℝn → ℝn , Φ(x) = Bjx + cj, functia iterativa prin care generam sirul iterativ (xk)k∈ℕ (xk+1=Φ(xk)=Bjxk + cj), atunci pentru orice
x,y ∈ℝn avem:
|| Φ(x) - Φ(y)||∞ = ||(Bjx + cj) - (Bjy + cj)||∞ = ||Bj(x - y)||∞ ≤ ||Bj||∞·||x - y||∞ .
Aceasta conditie exprima faptul ca Φ este o contractie pe ℝn avand constanta de contractie ||Bj||∞ < 1. Suntem gata cu demonstratia teoremei, fiindca este de ajuns sa aplicam teorema de punct fix a lui Banach pentru contractia Φ pe spatiul metric complet ℝn , unde metrica este generata de catre norma vectoriala maximum. q.e.d.
Presupunem ca sirul iterativ (xk)k∈ℕ⊂ℝn este convergent, si fie
limk→∞ xk = x*. Trecand la limita in recurenta xk+1 = Bjxk + cj pentru k→∞ obtinem ca x* = Bjx* + cj , ceea ce este echivalent cu Ax* = b. Prin urmare in acest fel generam un sir iterativ (xk)k∈ℕ care converge catre solutia sistemului initial A·x = b.
Capitolul 3: Metoda lui Jacobi pentru sistemele liniare infinite
3.1. Spatii de siruri: l1, l2, lp, l∞.
Spatiile Banach finit dimensionale reprezinta fara indoiala cea mai investigata clasa de spatii Banach si constituie un model si in acelasi timp un instrument pentru teoria infinit dimensionala.
Spatiile Banach finit dimensionale sunt reflexive, au baza, sunt complementate in orice spatiu Banach care le contine ca subspatii. Toate spatiile Banach de dimensiune n sunt izomorfe (algebric si topologic), astfel incat teoria izomorfa a acestor spatii este saraca. In schimb teoria izometrica ridica probleme interesante si profunde a caror solutionare necesita un aparat matematic complicat, bazat pe demonstrarea unei inegalitati foarte fine.
Cele mai simple spatii Banach finit dimensionale sunt spatiile lp (n), 1≤p≤∞, formate din toate n-uplurile a = (a1,,an) de scalari si inzestrate respectiv, cu norma:
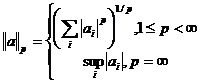
Exemple
Spatiul de siruri l1
= ![]() , adica suma seriei
trebuie sa fie o suma finita.
, adica suma seriei
trebuie sa fie o suma finita.
Exemplu: ![]()
Spatiul de siruri l2 ![]()
![]() deoarece
deoarece
![]() , dar
, dar
![]()
Spatiul de siruri lp: lp
= ![]()
Spatiul l
Vom vorbi in continuare si vom face o prezentare mai pe larg a spatiului general de siruri lp, cand p≥0.
Fie K o multime (K poate fi ℝ sau ℂ).
Fie un spatiu s =
Fie x,y∈s. x+y∈s, ∈k. 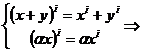 s este spatiu vectorial.
s este spatiu vectorial.
Pentru p>0, lp=![]()
Pentru p=0, l0=
Fie X un spatiu vectorial. Y⋐X. Y subspatiu vectorial a lui X
⇔![]()
3.1.1 Propozitie
Spatiul lp , cu p≥0, este spatiu vectorial.
Demonstratie
Vrem sa aratam ca lp este un subspatiu a lui s, adica lp⋐s.
Fie x = (xi)i∈ℕ,
x ∈ lp, ![]()
si y = (yi)i∈ℕ, y ∈ lp, ![]()
x + y = (xi + yi) i∈ℕ ⇒(?) (x + y) ∈ lp
|xi + yi|p ≤ (|xi| + |yi|)p ≤ (2⋅max)p =
= 2p⋅(max)p =
=2p⋅(max) ≤ 2p⋅(|xi|p + |yi|p)
![]() , aceasta suma este finita, deci apartine
lui lp.
, aceasta suma este finita, deci apartine
lui lp.
In continuare vom demonstra inegalitatea lui Young
Inegalitatea lui Young
Fie p,q>1, astfel incat ![]() . Atunci
. Atunci 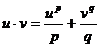 ,
, ![]()
Demonstratie
Fie ![]() t > 0.
t > 0.
t = 1 este punct
de minim. Se ia ![]()
![]() , t=1
, t=1
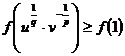
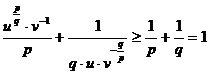
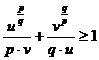 /⋅uv
/⋅uv
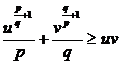
![]() ,
, ![]() , atunci
, atunci
![]()
Folosind inegalitatea lui Young, vom demonstra acum inegalitatea lui Hőlder.
Inegalitatea lui Hőlder
Fie p,q > 1. x ∈ lp, y lq. Atunci,
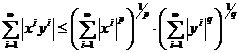 .
.
Daca am avea p=2, q=2, am
avea 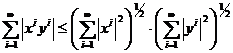
care este inegalitatea lui Cauchy - Buniakowski - Schwarz
Demonstratie
![]()
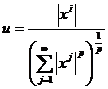 ,
, 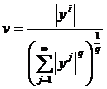
![]()
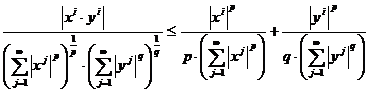
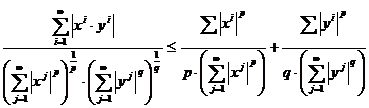
![]()
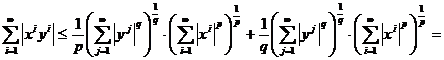
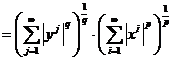 ;
; ![]()
Asadar 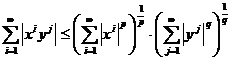
Folosind inegalitatea lui Hőlder, vom demonstra inegalitatea lui Minkowski
Inegalitatea lui Minkowski
Fie p ≥ 1 si x,y ∈ lp. Atunci:
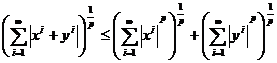
Demonstratie
p=1. ![]()
p>1 ![]()
![]()
ζ∈s, ζi=|xi+yi|p-1. ζ∈lq ⇔![]()
![]() , deoarece x,y ∈ lp
, deoarece x,y ∈ lp
continuam inegalitatea
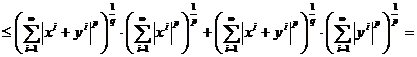
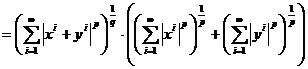
pentru ![]() adevarat
adevarat
altfel impartim cu 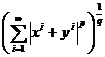 si rezulta
si rezulta
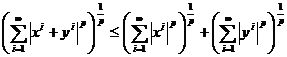 , ceea ce trebuia demonstrat.
, ceea ce trebuia demonstrat.
Cu
ajutorul inegalitatii lui Minkowski am demonstrat acum inegalitatea
triunghiului, deoarece ||x||p = 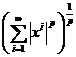 , care este norma pe lp. Si atunci:
, care este norma pe lp. Si atunci:
||x+y||p = ||x||p + ||y||p, care este o proprietate a normei.
3.2. Norme vectoriale pe spatii de siruri lp
3.2.1 Definitie
Fie 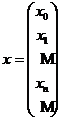 un sir de numere reale reprezentate in forma unui vector
infinit de tip coloana, si notam cu s spatiul liniar real
al acestor siruri. Fie
un sir de numere reale reprezentate in forma unui vector
infinit de tip coloana, si notam cu s spatiul liniar real
al acestor siruri. Fie
p ∈[1,+∞) un numar real si definim lp = .
Este binecunoscut ca lp
este un subspatiu liniar real al spatiului s si pentru orice x∈
lp formula 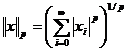 defineste o norma pe
lp. Astfel, (lp, ||·||p) nu
doar ca este un spatiu normat liniar, ci si un spatiu
Banach, de asemenea. Pentru p=1 si p=2 vom reobtine spatiul
Banach l1 si respectiv,
spatiul Hilbert l2. In l2
vom considera produsul scalar standard dat de formula (x,y) =
defineste o norma pe
lp. Astfel, (lp, ||·||p) nu
doar ca este un spatiu normat liniar, ci si un spatiu
Banach, de asemenea. Pentru p=1 si p=2 vom reobtine spatiul
Banach l1 si respectiv,
spatiul Hilbert l2. In l2
vom considera produsul scalar standard dat de formula (x,y) = ![]() pentru orice x, y ∈ l2. Pentru p,q ∈[1,+∞) numere reale, p<q
rezulta lp⊂lq. Daca s0
este un subspatiu liniar al sirurilor convergente la 0 atunci lp ⊂ s0
pentru orice p ∈[1,+∞). Vom considera de asemenea subspatiul
liniar l∞ = . Pentru orice x∈ l∞ formula
pentru orice x, y ∈ l2. Pentru p,q ∈[1,+∞) numere reale, p<q
rezulta lp⊂lq. Daca s0
este un subspatiu liniar al sirurilor convergente la 0 atunci lp ⊂ s0
pentru orice p ∈[1,+∞). Vom considera de asemenea subspatiul
liniar l∞ = . Pentru orice x∈ l∞ formula
||x||∞
= ![]() defineste o norma pe l∞.
Astfel, (l∞, ||·||∞)
nu este doar un spatiu liniar normat ci si un spatiu Banach de
asemenea. Avem: l1 ⊂
l2 ⊂ s0 ⊂
l∞ ⊂ s. Toate
aceste spatii le vom numi spatii vectoriale cu elemente vectori
si mai sus mentionatele norme vectoriale.
defineste o norma pe l∞.
Astfel, (l∞, ||·||∞)
nu este doar un spatiu liniar normat ci si un spatiu Banach de
asemenea. Avem: l1 ⊂
l2 ⊂ s0 ⊂
l∞ ⊂ s. Toate
aceste spatii le vom numi spatii vectoriale cu elemente vectori
si mai sus mentionatele norme vectoriale.
Norme matriciale pentru matrici infinite
3.3.1 Teorema
Fie A=(aij)i,j∈ℕ o matrice infinita
de numere reale si vom nota cu M
spatiul liniar real al acestor matrici infinite. Fie M1 = . Atunci M1 este un subspatiu liniar real al lui M si pentru fiecare A∈M1, formula ![]() defineste o
norma pe M1 numita
norma coloana. Astfel, (M1, ||·||1) devine
nu numai un spatiu normat linear real, ci si un spatiu Banach, de
asemenea.
defineste o
norma pe M1 numita
norma coloana. Astfel, (M1, ||·||1) devine
nu numai un spatiu normat linear real, ci si un spatiu Banach, de
asemenea.
Fie p∈(1, +∞) un numar real si definim
Mp = , unde q este un numar
real astfel incat ![]() .
.
Teorema
Spatiul Mp este un subspatiu real liniar al lui M si pentru orice A∈Mp, formula
||A||p
= 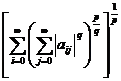
defineste o norma pe Mp. Spatiul (Mp, ||·||1) este un spatiu Banach.
Demonstratie
Folosind de doua ori inegalitatea lui Minkowski vom obtine:
||A+B||p = 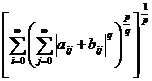 =
=
= 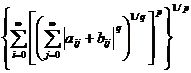 ≤
≤
≤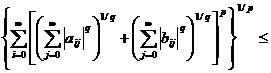
≤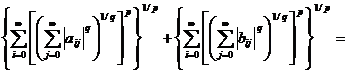
=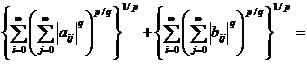
=||A||p + ||B||p.
Pentru α∈ℝ si A∈ Mp avem
A||p
= 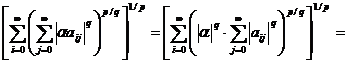
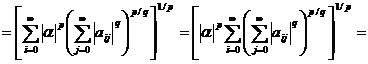
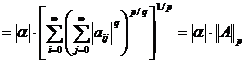 .
.
In final obtinem ||A||p
≥ 0 si ||A||p = 0 de unde rezulta 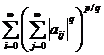 =0, deci aij =0
pentru orice i,j ∈ℕ , adica A = O∞ , unde O∞
inseamna matricea nula.
=0, deci aij =0
pentru orice i,j ∈ℕ , adica A = O∞ , unde O∞
inseamna matricea nula.
Fie (An)n∈ℕ
, An = ![]() , un sir fundamental in
spatiul normat
, un sir fundamental in
spatiul normat
(Mp, ||·||p), adica pentru orice Ɛ>0 exista nƐ ∈ℕ astfel incat pentru orice
n,m≥ nƐ, ||An-Am||p≤Ɛ. Oricare ar fi i0,j0∈ℕ numere naturale fixate, vom obtine:
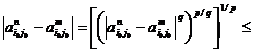
=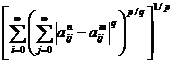 =
=
= ||An-Am||p ≤ Ɛ.
In
consecinta, pentru fiecare i0,j0∈ℕ,
sirul de numere reale ![]() este fundamental, ceea
ce implica convergenta acestui sir in ℝ. Fie
este fundamental, ceea
ce implica convergenta acestui sir in ℝ. Fie ![]() ℝ astfel incat
ℝ astfel incat ![]() si vom construi matricea A=(ai0j0)i0,j0∈ℕ.
Vom folosi notatia
si vom construi matricea A=(ai0j0)i0,j0∈ℕ.
Vom folosi notatia ![]() deoarece
deoarece ![]() pentru orice i,j∈ℕ.
Acum, folosind continuitatea normei ||·||p, din inegalitatea ||An-Am||p≤Ɛ
adevarat pentru orice n,m≥nƐ vom avea:
pentru orice i,j∈ℕ.
Acum, folosind continuitatea normei ||·||p, din inegalitatea ||An-Am||p≤Ɛ
adevarat pentru orice n,m≥nƐ vom avea:
![]() , adica ||An-Am||p≤Ɛ,
oricare ar fi n≥nƐ.
, adica ||An-Am||p≤Ɛ,
oricare ar fi n≥nƐ.
Asta inseamna ca sirul (An)n∈ℕ este convergent la matricea A in norma ||·||p. Dar, ||A||p≤||A-An0||p+||An0||p≤Ɛ+||An0||p,
Pentru un punct fixat n0∈ℕ, n0≥nƐ.
Asadar A∈Mp, ceea ce incheie aceasta demonstratie.
Pentru p=2 vom obtine M2 = . Daca luam in M2
produsul scalar dat de formula (A,B) = ![]() , unde A = (aij)i,j∈ℕ
si
, unde A = (aij)i,j∈ℕ
si
B = (bij)i,j∈ℕ atunci (M2, (·,·)) va fi un spatiu Hilbert.
Fie M∞ = .Atunci M∞
este un subspatiu liniar real al lui M si pentru orice A∈M∞, formula
||A||∞ = ![]() defineste o norma pe M∞, numita norma
linie. Astfel, (M∞,
||·||∞) devine nu numai un spatiu liniar normat, ci
si un spatiu Banach.
defineste o norma pe M∞, numita norma
linie. Astfel, (M∞,
||·||∞) devine nu numai un spatiu liniar normat, ci
si un spatiu Banach.
3.3.3. Corolar
Daca pentru matricea A=(aij)i,j∈ℕ avem aij = 0 pentru i>n sau j>n, n∈ℕ, atunci din teorema de mai sus vom reobtine rezultatele in spatiul finit dimensional ℝn.
Toate aceste spatii le vom numi spatii matriciale si mai sus mentionatele norme, norme matriciale.
3.4. Compatibilitatea normelor vectoriale cu normele matriciale in lp
Fie x ∈ s un sir de numere reale si A=(aij)i,j∈ℕ ∈M o matrice infinita de numere reale.
3.4.1.
Definitie Vom defini produsul A·x
daca pentru fiecare i∈ℕ, seriile ![]() sunt convergente. In
acest caz vectorul rezultat y = A·x este un vector coloana cu componentele
sunt convergente. In
acest caz vectorul rezultat y = A·x este un vector coloana cu componentele
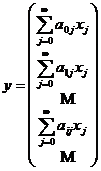 .
.
3.4.2. Teorema
Pentru orice p ∈ [1, +∞] = [1, +∞) ∪ , norma vectoriala ||·||p definita pe lp este compatibila cu norma matriciala ||·||p definita pe Mp , adica ||Ax||p ≤ ||A||p ·||x||p oricare ar fi x∈ lp si oricare ar fi A ∈ Mp .
Demonstratie
Fie p=1. Atunci
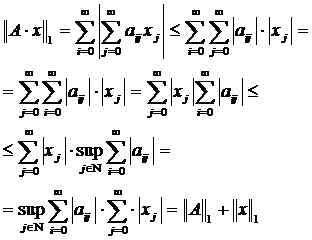
Fie p ∈ [1, +∞]. Folosind inegalitatea lui Hölder vom obtine
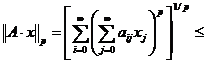
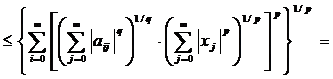
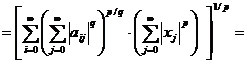
=
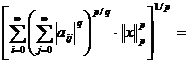
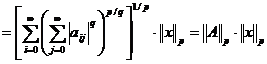 .
.
Fie p = +∞. Atunci,
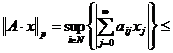
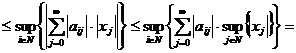
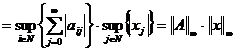 .
.
3.4.3. Corolar
Daca pentru matricea A=(aij)i,j∈ℕ avem aij = 0 pentru i>n sau j>n, n∈ℕ, atunci din teorema 3.4.2. vom reobtine rezultatele in spatiul finit dimensional ℝn.
3.5. Norme matriciale subordonate normelor vectoriale in lp
Pentru orice p ∈[1, +∞] si
pentru orice x ∈ lp si A ∈ Mp avem ||Ax||p ≤ ||A||p ·||x||p
conform teoremei 3.4.2. Daca x ≠ ![]() (elementul nul al spatiului vectorial lp),
atunci
(elementul nul al spatiului vectorial lp),
atunci 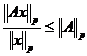 si putem defini
si putem defini 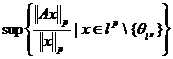 . Se stie ca aceasta formula
defineste o norma matriciala pe Mp pe care o putem numi norma matriciala
subordonata normei vectoriale ||·||p definita pe lp
si notam cu
. Se stie ca aceasta formula
defineste o norma matriciala pe Mp pe care o putem numi norma matriciala
subordonata normei vectoriale ||·||p definita pe lp
si notam cu 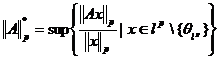 . Este evident ca
. Este evident ca ![]() pentru orice A ∈
Mp .
pentru orice A ∈
Mp .
3.5.1. Teorema
Pentru orice p∈ avem
![]()
Demonstratie
Fie p=1. Stim
ca ![]() . Trebuie sa
aratam ca
. Trebuie sa
aratam ca ![]() . Din
. Din ![]() rezulta ca :
pentru orice ℇ>0 exista un
j0∈ℕ astfel incat
rezulta ca :
pentru orice ℇ>0 exista un
j0∈ℕ astfel incat ![]() . Alegem vectorul x∈l1
astfel incat toate componentele lui x sunt zero, cu exceptia componentei j0.
Deci
. Alegem vectorul x∈l1
astfel incat toate componentele lui x sunt zero, cu exceptia componentei j0.
Deci
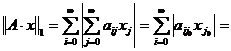
![]()
![]() .
.
In consecinta,
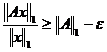 ,
,
adica
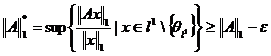
pentru orice ℇ>0. asta inseamna ca ![]() .
.
Fie p=+∞. Avem ![]() . Trebuie sa demonstram ca
. Trebuie sa demonstram ca ![]() .
.
Din ||A||∞![]() obtinem: pentru orice ℇ>0
atunci exista i0∈ℕ astfel incat
obtinem: pentru orice ℇ>0
atunci exista i0∈ℕ astfel incat
![]() . Alegem un vector x∈l∞ astfel incat componenta j∈ℕ a lui x
este egala cu xj=sign(ai0j), oricare ar fi j∈ℕ,
unde sign este functia semn.
. Alegem un vector x∈l∞ astfel incat componenta j∈ℕ a lui x
este egala cu xj=sign(ai0j), oricare ar fi j∈ℕ,
unde sign este functia semn.
Deci ||x||∞=1 si
![]()
![]()
![]()
In consecinta,
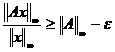 , adica
, adica
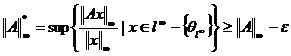
oricare ar fi ℇ>0. Asta inseamna
ca ![]() .
.
3.5.2. Corolar
Daca pentru matricea A = (aij)I,j∈ℕ avem aij=0 pentru i>n sau j>n, n∈ℕ, atunci din teorema 3.5.1. vom reobtinem rezultatele in spatiul finit dimensional ℝn.
Mentionam ca este necunoscut cum putem calcula pentru p∈(1,+∞) norma matriciala subordonata normei vecoriale ||⋅||p definita pe lp.
Spatiile vectoriale si matriciale mai sus prezentate le vom folosi pentru a extinde metoda lui Jacobi, cunoscuta ca metoda iterativa numerica, din sisteme liniare finite la sisteme liniare infinite. In acest fel putem studia procesele liniare stationare cu un numar de parametri infinit dar numarabil..
3.6. Metoda lui Jacobi pentru sistemele liniare infinite
Mai intai sa ne reamintim bine-cunoscuta teorema de punct fix a lui Banach pentru spatiile Banach
3.6.1. Teorema
Fie ( X, ||⋅||x ) un spatiu Banach, si φ o contractie (exista o constanta α∈(0,1) astfel incat || (x)- (y)||x ≤ ⋅ ||x-y||x , oricare ar fi x,y ∈ X). Atunci pentru orice x0 ∈ X sirul (xk)k∈ℕ, generat de formula recursiva xk+1 = (xk), este convergent si are limita in punctul x* ∈ X, care este un punct unic, fix, al functiei φ in X.
Sa consideram sistemul liniar infinit de ecuatii Ax = b, unde A∈M si x,b ∈ s .
3.6.2. Definitie
Se da A ∈ M si b ∈ s. Vom spune ca x* ∈ s este solutie a sistemului liniar infinit de ecuatii Ax = b si avem Ax* = b.
Asta inseamna ca toate aceste serii ![]() sunt convergente
si avem
sunt convergente
si avem
![]() , oricare ar fi i ∈ ℕ.
, oricare ar fi i ∈ ℕ.
Sa presupunem ca aii
≠ 0 pentru orice i ∈ ℕ. Atunci ecuatia ![]() este echivalenta
cu ecuatia
este echivalenta
cu ecuatia
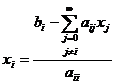 , adica
, adica
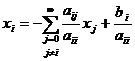 .
.
Asadar sistemul initial de ecuatii liniare Ax = b este echivalent cu urmatorul sistem iterativ de ecuatii liniare: x = Bjx + c, unde
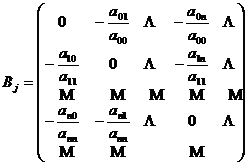 si
si 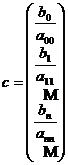 .
.
Alegem x0 ∈ s si generam sirul (xk)k∈ ℕ ⊂ s dupa urmatoarea formula iterativa: xk+1 = Bj⋅xk + c.
3.6.3. Definitie
Matricea A = (aij)i,j∈ ℕ
este l1 dominant
diagonala daca exista λ ∈ (0,1) astfel incat pentru
fiecare j ∈ ℕ avem λ⋅|ajj| > ![]()
Este imediat evident ca A este l1 dominant diagonala daca si numai daca
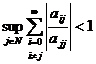 .
.
3.6.4. Definitie
Matricea A = (aij)i,j∈ℕ
este lp dominant
diagonala daca exista constanta pozitiva αi
> 0 pentru i∈ℕ astfel incat 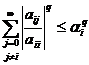 si
si ![]() ,
,
unde p > 1 si
![]() .
.
Este imediat evident ca A este lp dominant diagonala daca si numai daca
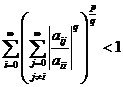 .
.
3.6.5 Definitie
Matricea A = (aij)i,j∈ℕ
este l∞ dominant
diagonala daca exista λ ∈ (0,1) astfel incat pentru fiecare i ∈ ℕ
avem λ⋅|aii| > ![]()
Este imediat evident ca A este l∞ dominant diagonala daca si numai daca
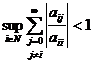 .
.
3.6.6 Teorema
Daca A este lp dominant diagonala, unde p ∈ [1, +∞], atunci sirul iterativ (xk)k∈ℕ este convergent in lp oricare ar fi x0 ∈ lp. Punctul limita x* ∈ lp este unica solutie a sistemului liniar Ax = b.
Demonstratie
Conditia ca A sa fie lp dominant diagonala este echivalenta cu ||Bj||p < 1 pentru orice p ∈ [1,+∞]. Astfel putem aplica teorema de punct fix a lui Banach pentru functii iterative : lp → lp, φ(x) = Bj⋅x + c. Intr-adevar, φ este o contractie pe lp , deoarece || (x) - (y)||p = ||(Bj⋅x + c) - (Bj⋅y + c) ||p =
= ||Bj(x - y) ||p ≤ ||Bj||p ⋅ ||x - y||p.
Asta inseamna ca sirul (xk)k∈ℕ este convergent in lp oricare ar fi x0 ∈ lp si punctul limita x* ∈ lp este unicul punct fix din φ in lp, astfel incat φ(x*) = x*.
Deci Bj ⋅ x* + c = x*, ceea ce este echivalent cu Ax* = b.
3.6.7 Consecinta
Daca pentru matricea A = (aij)i,j∈ℕ avem aij = 0, unde i > n sau j > n, si
bi = 0 pentru i > n, n ∈ ℕ , atunci vom reobtine sistemul linear cu numar finit de ecuatii si numar finit de necunoscute. Astfel din teorema 3.6.6 obtinem metoda clasica numerica iterativa a lui Jacobi de rezolvare a sistemelor liniare finite de ecuatii.
Bibliografie
[1] Cristescu M., Analiza matematica, Editura Universitatii "Petru
Maior" Targu Mures, 2003
[2] Finta B., Analiza numerica, Editura Universitatii "Petru Maior"
Targu Mures, 2004
[3] Finta B., Jacobi's Theorem for Infinte Systems of Linear Equations,
volum omagial, Profesor Gheorghe Farcas la varsta de 70 de ani,
Editura Universitatii "Petru Maior" Targu - Mures, pag. 103-108,
2004
[4] Gaspar D., Analiza functionala, Editura Facla, Timisoara, 1981
[5] Niculescu C., Popa N., Elemente din teoria spatiilor Banach Editura Academiei, Bucuresti, 1981
[6] Paltineanu G., Analiza matematica, Calcul diferential, Editura Agir, Bucuresti, 2002
|
Politica de confidentialitate |
| Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |