Legi de compozitie
 Lege de compozitie
Lege de compozitie
Definitia produsului cartezian :
Fie ![]() o multime nevida ;
o multime nevida ;
- Prin produsul cartezian ![]() intelegem multimea tuturor perechilor de
elemente
intelegem multimea tuturor perechilor de
elemente
![]()
unde : prima componenta este ![]() iar cea de-a doua este
iar cea de-a doua este ![]() , cand
, cand ![]() , adica :
, adica :
![]()
Definitia legii de compozitie :
Fie ![]() o multime nevida ;
o multime nevida ;
- Se numeste operatie algebrica binara sau lege de compozitie interna sau simplu lege
de compozitie definita pe ![]() o aplicatie :
o aplicatie :
![]() ,
, ![]()
care asociaza fiecarei perechi ![]() unicul element
unicul element ![]() .
.
- Elementul ![]() se numeste compusul
lui
se numeste compusul
lui ![]() cu
cu ![]() .
.
Observatii :
La orice
pereche (cuplu) ![]() =
=![]() , aceasta
operatie face sa corespunda in
, aceasta
operatie face sa corespunda in
mod unic elementul ![]() din aceeasi multime
din aceeasi multime ![]() .
.
Uneori in loc de ![]() se poate scrie :
se poate scrie : ![]() .
.
Pentru elementul ![]() , numit
compusul lui
, numit
compusul lui ![]() , se
, se
pot folosi diferite notatii :
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , etc.
, etc.
Se intelege ca in majoritatea cazurilor aceste denumiri sunt conventionale .
In general pe ![]() se pot defini mai multe operatii
diferite .
se pot defini mai multe operatii
diferite .
Cand dorim sa punem in evidenta una dintre ele vom utiliza parantezele :
![]()
si vom spune ca
operatia ![]() confera multimii
confera multimii ![]() o structura algebrica sau ca
o structura algebrica sau ca ![]()
este un sistem algebric .
Definitia legii de compozitie ADITIVA :
- Aplicatia : ![]() ,
, ![]() cu :
cu :
![]()
desemneaza o lege de compozitie aditiva .
Definitia legii de compozitie MULTIPLICATIVA :
- Aplicatia : ![]() ,
, ![]() cu :
cu :
![]()
desemneaza o lege de compozitie multiplicativa .
Concluzie :
- Fie ![]() o multime nevida ;
o multime nevida ;
- Numim lege de compozitie interna ( operatie algebrica ) pe multimea ![]() orice functie
orice functie
definita pe ![]() cu valori in
cu valori in ![]() :
:
![]() ,
, ![]()
care asociaza fiecarui cuplu ![]() un unic element
un unic element ![]() .
.
- Elementul ![]() se citeste :
se citeste : ![]() ( sau
( sau ![]() ) in
aceasta
) in
aceasta
ordine .
Important :
Fie
![]() o multime nevida si legea
o multime nevida si legea ![]() ;
;
- Cuplul ![]() este
un sistem algebric sau vom spune ca operatia
este
un sistem algebric sau vom spune ca operatia ![]() confera multimii
confera multimii ![]() o structura algebrica
o structura algebrica
daca si numai daca
pentru aplicatia : ![]() ,
, ![]()
avem :
![]() ,
, ![]() .
.


Introducere :
- Fie ![]() o structura algebrica ;
o structura algebrica ;
- Si ![]() o submultime nevida a lui
o submultime nevida a lui ![]() ,
, ![]() ;
;
- Este posibil ca pentru ![]() elementul
elementul ![]() sa fie :
sa fie :
In
multimea ![]() , adica
, adica ![]() ;
;
Sau sa
fie in afara ei , adica ![]() .
.
Definitie parte stabila :
- Pentru orice ![]() , compusul
, compusul ![]() apartine tot lui
apartine tot lui ![]() , adica
, adica ![]() , atunci putem
spune ca
, atunci putem
spune ca ![]() este parte stabila a lui
este parte stabila a lui ![]() in raport cu operatia
in raport cu operatia ![]() .
.
Concluzie :
- Daca ![]() este o parte stabila a lui
este o parte stabila a lui ![]() in raport cu legea de compozitie
in raport cu legea de compozitie ![]()
atunci pe ![]() putem defini legea de
compzitie :
putem defini legea de
compzitie :
![]()
punand :
![]() ,
, ![]() .
.
- Vom spune ca ![]() este legea de compozitie pe
este legea de compozitie pe ![]() de catre
de catre ![]() .
.

P
- Fie ![]() o multime finita ,
o multime finita , ![]() ;
;
P
- O lege de compozitie ![]() pe
pe ![]() ,
, ![]() , poate fi data prin ceea ce este
, poate fi data prin ceea ce este
cunoscut sub
numele de tabla operatiei ![]() , care
consta dintr-un tabel cu
, care
consta dintr-un tabel cu ![]() linii si
linii si ![]() coloane
coloane
afectate celor ![]() elemente ale
lui
elemente ale
lui ![]() .
.
P
- Tabla legii de compozitie ![]() contine la intersectia liniei lui
contine la intersectia liniei lui ![]() cu coloana
cu coloana ![]() elementul
elementul ![]() .
.
|
|
|
|
|
|
|
||||
|
| |||||||||
|
| |||||||||
|
|
| ||||||||
|
|
| ||||||||
|
|
Observatii :
Din tabla unei operatii pe o multime finita putem deduce urmatoarele proprietati :
1). Daca multimea ![]() este parte stabila in raport cu legea
este parte stabila in raport cu legea ![]() este o lege de compozitie pe
este o lege de compozitie pe
![]() ( constatand ca toate rezultatele compunerilor
( constatand ca toate rezultatele compunerilor
![]() sunt din
sunt din ![]() ) .
) .
2). - comutativitatea ;
- elementul neutru , (daca exista ) ;
- simetricul fiecarui element , (daca are ) .

Exercitiul nr. 1 : ( Schneider )
Sa se arate in fiecare din urmatoarele cazuri ca
multimea ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport cu legea de compozitie specificata :
in raport cu legea de compozitie specificata :
1). ![]() ,
, ![]() ,
, ![]() ;
;
2). ![]() ,
, ![]() ,
, ![]() ;
;
3). ![]() ,
, ![]() ,
, ![]() ;
;
4). ![]() ,
, ![]() ,
, ![]() ;
;
5). ![]() ,
, ![]() ,
, ![]() ;
;
6). ![]() ,
, ![]() ,
, ![]() ;
;
7). 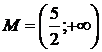 ,
, ![]() ,
, 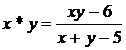 ;
;
8). ![]() ,
, ![]() ,
, 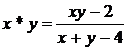 ;
;
9). ![]() ,
, ![]() ,
, 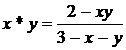 ;
;
10). ![]() ,
, ![]() ,
, 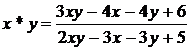 ;
;
11). ![]() ,
, ![]() ,
, ![]() ;
;
12). 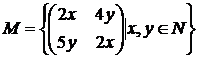 ,
, ![]() , inmultirea matricilor ;
, inmultirea matricilor ;
13). 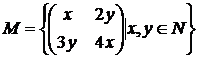 ,
, ![]() , adunarea matricilor ;
, adunarea matricilor ;
14). ![]() ,
, ![]() , inmultirea numerelor reale .
, inmultirea numerelor reale .
Exercitiul nr. 2 : ( Mircea Ganga )
Sa se arate ca : ![]() este parte stabila a
lui
este parte stabila a
lui ![]() ia raport cu operatia
de inmultire .
ia raport cu operatia
de inmultire .
Exercitiul nr. 3 : (Mircea Ganga )
Pe ![]() se considera legea de
compozitie :
se considera legea de
compozitie : ![]() .
.
Sa se arate ca ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport cu
legea
in raport cu
legea ![]() .
.
Exercitiul nr. 4 : (Mircea Ganga )
Pe ![]() se considera
legea
se considera
legea ![]() .
.
Sa se arata
ca ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport cu
legea
in raport cu
legea ![]() .
.
Exercitiul nr. 5 : (Mircea Ganga )
Pe ![]() consideram legea de
compozitie :
consideram legea de
compozitie : ![]() . Aratati ca
. Aratati ca ![]() este o parte stabila a
lui
este o parte stabila a
lui ![]() ia raport cu
legea
ia raport cu
legea ![]() .
.
Exercitiul nr. 6 : (Mircea Ganga )
Fie 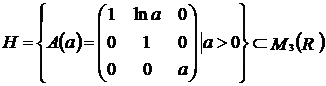 . Aratati ca
. Aratati ca ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport cu operatia
de inmultire .
in raport cu operatia
de inmultire .
Exercitiul nr. 7 : (Mircea Ganga )
Fie 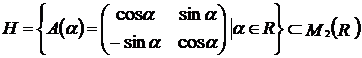 . Sa se arate ca
. Sa se arate ca ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport cu operatia
de inmultire .
in raport cu operatia
de inmultire .
Exercitiul nr. 8 : (Mircea Ganga )
Fie 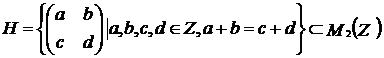 . Aratati ca
. Aratati ca ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport cu operatia
de inmultire a matricilor .
in raport cu operatia
de inmultire a matricilor .
Exercitiul nr. 9 : (Mircea Ganga )
Fie 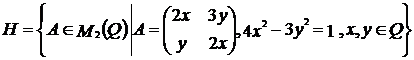 . Aratati ca
. Aratati ca ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport inmultirea
matricilor .
in raport inmultirea
matricilor .
Exercitiul nr. 10 : (Mircea Ganga )
Pe ![]() se defineste legea de
compozitie
se defineste legea de
compozitie ![]() prin
prin ![]() . Sa se
determine
. Sa se
determine ![]() astfel incat
multimea
astfel incat
multimea ![]() sa fie parte stabila
a lui
sa fie parte stabila
a lui ![]() in raport cu
legea
in raport cu
legea ![]() .
.
Exercitiul nr. 11 : (Teste grila admitere Poli )
Multimea valorilor lui ![]() , pentru care
intervalul
, pentru care
intervalul ![]() este parte stabila in
raport cu operatia
este parte stabila in
raport cu operatia ![]() .
.


![]()

P
Vom
considera structura algebrica ![]()
Adica ![]() o multime nevida echipata cu o lege de
compozitie
o multime nevida echipata cu o lege de
compozitie ![]() :
:
![]() ,
, ![]() .
.
Definitie ASOCIATIVITATII :
- O lege de compozitie ![]() ,
, ![]() se numeste asociativa
daca :
se numeste asociativa
daca :
![]() ,
, ![]()
Observatii Asociativitate :
1). Daca legea ![]() este asociativa , atunci se omit in scriere
parantezele si se scrie simplu
este asociativa , atunci se omit in scriere
parantezele si se scrie simplu
![]()
2). Vom da acelasi nume structurii algebrice ![]() definita prin legea
definita prin legea ![]() , adica vom
, adica vom
spune ca este o structura algebrica asociativa , sau spunem simplu ca legea
este asociativa pe ![]()
3). Daca ![]() este o parte stabila a lui
este o parte stabila a lui ![]() in raport cu legea
in raport cu legea ![]() si daca
si daca ![]() este
este
asociativa pe ![]() , atunci legea
, atunci legea ![]() ramane asociativa si pe
ramane asociativa si pe ![]() . Altfel spus
. Altfel spus ![]() devine o
devine o
structura algebrica asociativa .
4). O lege ![]() nu este asociativa daca exista
nu este asociativa daca exista ![]() pentru care :
pentru care :
![]()

Exercitiul nr. 1 : ( Schneider )
Sa se arate ca urmatoarele legi de compozitie sunt asociative :
1). ![]() pe
pe ![]() ;
;
2). ![]() pe
pe ![]() ;
;
3). ![]() pe
pe ![]() ;
;
4). 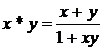 pe
pe ![]() ;
;
5). ![]() pe
pe ![]() ;
;
6). Inmultirea matricilor pe 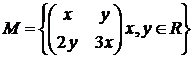 ;
;
7). ![]() pe
pe ![]() ;
;
8). ![]() pe
pe ![]() .
.
Exercitiul nr. 2 : ( Schneider )
Sa se arate ca urmatoarele legi de compozitie nu sunt asociative :
1). ![]() pe
pe ![]() ;
;
2). ![]() pe
pe ![]() ;
;
3). ![]() pe
pe ![]() ;
;
4). 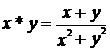 pe
pe ![]() .
.
Exercitiul nr. 3 : ( Ganga )
Stabiliti care
din urmatoarele aplicatii sunt algebrice asociative pe submultimea ![]() :
:
![]() 2).
2). ![]()
3). ![]() 4).
4). ![]()
5). ![]() 6).
6). ![]()
7). ![]() 8).
8). ![]() .
.
Exercitiul nr. 4 : ( Ganga )
Pe ![]() se definesc urmatoarele legi de
compozitie :
se definesc urmatoarele legi de
compozitie :
1). ![]() 2).
2). ![]()
3). ![]() 4).
4). ![]()
5). ![]() 6).
6). ![]()
Care din aceste legi este asociativa ?
Exercitiul nr. 5 : ( Ganga )
Fie 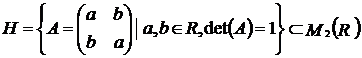 .
.
Aratati ca :
1). ![]() este parte stabile a lui
este parte stabile a lui ![]() in raport cu
inmultirea matricilor .
in raport cu
inmultirea matricilor .
2). ![]() este structura
algebrica asociativa .
este structura
algebrica asociativa .
Exercitiul nr. 6 : ( Ganga )
Pe ![]() se considera legea de compozitie :
se considera legea de compozitie : ![]() ,
, ![]() . Sa se determine
. Sa se determine ![]()
astfel incat legea sa fie asociativa .
Exercitiul nr. 7 : ( Ganga )
Pe ![]() se considera legea de compozitie :
se considera legea de compozitie : ![]() ,
, ![]() . Determinati
. Determinati ![]() astfel incat legea sa
fie asociativa .
astfel incat legea sa
fie asociativa .
Exercitiul nr. 8 : ( Ganga )
Pe ![]() definim legile de compozitie :
definim legile de compozitie :
![]() ,
, ![]() ,
, ![]()
Determinati ![]() astfel incat
operatiile sa fie asociative .
astfel incat
operatiile sa fie asociative .
![]()

P
Vom
considera structura algebrica ![]()
adica ![]() o multime nevida echipata cu o lege de
compozitie
o multime nevida echipata cu o lege de
compozitie ![]() :
:
![]() ,
, ![]() .
.
Definitie COMUTATIVITATE :
- O lege de compozitie ![]() ,
, ![]() se numeste comutativa
daca :
se numeste comutativa
daca :
![]() ,
, ![]()
Observatii Comutativitate :
1). Daca pentru structura algebrica ![]() definita prin
definita prin ![]() avem ca
avem ca ![]() este
este
comutativa ,
atunci structura algebrica este comutativa sau simplu spunem ca ![]() este
este
comutativa pe ![]() .
.
2). Daca ![]() este o parte stabila a lui
este o parte stabila a lui ![]() in raport cu legea
in raport cu legea ![]() si daca
si daca ![]() este
este
comutativa pe ![]() , atunci legea
, atunci legea ![]() ramane comutatuva si pe
ramane comutatuva si pe ![]() . Altfel spus
. Altfel spus ![]()
devine o structura algebrica comutativa .
4). O lege ![]() nu este comutativa daca exista
nu este comutativa daca exista ![]() astfel incat :
astfel incat :
![]()

Exercitiul nr. 1 : ( Schneider )
Sa se arate ca urmatoarele legi de compozitie sunt comutative :
1). ![]() pe
pe ![]() ;
;
2). 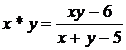 pe
pe 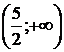 ;
;
3). ![]() pe
pe ![]() ;
;
4). ![]() pe
pe ![]() .
.
Exercitiul nr. 2 : ( Schneider )
Sa se arate ca urmatoarele legi de compozitie nu sunt comutative :
1). Inmultirea matricilor pe multimea :
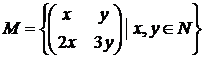 ;
;
2). Inmultirea matricilor pe multimea :
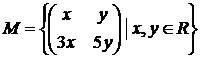 ;
;
3). ![]() pe
pe ![]() ;
;
4). ![]() pe
pe ![]() .
.
Exercitiul nr. 3 : ( Ganga )
Fie ![]() si pe
si pe ![]() legea de
compozitie :
legea de
compozitie :
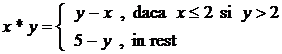
Aratati ca ![]() este structura
necomutativa .
este structura
necomutativa .
Exercitiul nr. 4 : ( Ganga )
Pe ![]() se considera legea de
compozitie :
se considera legea de
compozitie : ![]() . Fie
. Fie ![]() . Aratati ca
. Aratati ca ![]() este o structura
algebrica comutativa .
este o structura
algebrica comutativa .
Exercitiul nr. 5 : ( Ganga )
Fie 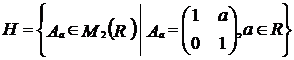 . Aratati ca
. Aratati ca ![]() este structura
algebrica comutativa , unde
este structura
algebrica comutativa , unde ![]() este inmultirea
obisnuita a matricilor .
este inmultirea
obisnuita a matricilor .
Exercitiul nr. 6 : ( Ganga )
Fie ![]() si aplicatia
si aplicatia ![]() . Sa se arate ca
. Sa se arate ca ![]() este o
este o
structura algebrica comutativa .
Exercitiul nr. 7 : ( Ganga )
Pe ![]() se defineste legea de
compozitie :
se defineste legea de
compozitie : ![]() . Aratati ca
. Aratati ca ![]() este o lege
necomutativa .
este o lege
necomutativa .
Exercitiul nr. 8 : ( Ganga )
Pe multimea ![]() se considera
aplicatia :
se considera
aplicatia : ![]() . Aratati ca
. Aratati ca ![]() este structura
algebrica comutativa .
este structura
algebrica comutativa .
Exercitiul nr. 9 : ( Ganga )
Pe multimea ![]() se considera
aplicatia :
se considera
aplicatia : 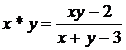 . Demonstrati ca
. Demonstrati ca ![]() este structura
algebrica comutativa .
este structura
algebrica comutativa .
Exercitiul nr. 10 : ( Ganga )
Se considera 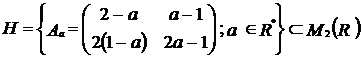 . Demonstrati ca
structura algebrica
. Demonstrati ca
structura algebrica ![]() este structura
algebrica comutativa , unde
este structura
algebrica comutativa , unde ![]() este inmultirea
obisnuita a matricilor .
este inmultirea
obisnuita a matricilor .
Exercitiul nr. 11 : ( Ganga )
Fie 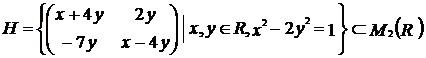 . Aratati ca
. Aratati ca ![]() este structura
algebrica comutativa .
este structura
algebrica comutativa .
Exercitiul nr. 12 : ( Ganga )
Se considera ![]() si aplicatia
si aplicatia ![]() . Sa se arate ca
. Sa se arate ca ![]() este o
este o
structura algebrica comutativa .
Exercitiul nr. 13 : ( Ganga )
Pe ![]() se defineste legea de
compozitie definita prin :
se defineste legea de
compozitie definita prin : ![]() ,
, ![]() .
.
Determinati ![]() pentru care legea
este asociativa si comutativa .
pentru care legea
este asociativa si comutativa .
![]()

P
Vom
considera structura algebrica ![]()
adica ![]() o multime nevida echipata cu o lege de
compozitie
o multime nevida echipata cu o lege de
compozitie ![]() :
:
![]() ,
, ![]() .
.
Definitie ELEMENT NEUTRU :
Un
element ![]() se numeste element neutru pentru o lege de compozitie
se numeste element neutru pentru o lege de compozitie
![]() ,
, ![]() daca :
daca :
![]() ,
, ![]()
Teorema :
- Daca o lege de compozitie admite element neutru , atunci acesta este unic .
Observatii Element neutru :
1). Daca ![]() este o parte stabila a lui
este o parte stabila a lui ![]() in raport cu
legea
in raport cu
legea ![]() si daca
si daca ![]() este
este
element neutru
pentru legea ![]() , atunci daca
, atunci daca ![]() . acesta ete element neutru al legii
. acesta ete element neutru al legii
induse de ![]() pe multimea
pe multimea ![]() .
.
Definitie ELEMENT NEUTRU la stanga :
Un
element ![]() se numeste element neutru la stanga pentru o lege de compozitie :
se numeste element neutru la stanga pentru o lege de compozitie :
![]() ,
, ![]() ,
, ![]() daca :
daca :
![]() ,
, ![]() .
.
Definitie ELEMENT NEUTRU la dreapta :
Un
element ![]() se numeste element neutru la dreapta pentru o lege de compozitie :
se numeste element neutru la dreapta pentru o lege de compozitie :
![]() ,
, ![]() ,
, ![]() daca :
daca :
![]() ,
, ![]()
Important :
- Daca un element ![]() este element neutru
pentru legea
este element neutru
pentru legea ![]() daca si numai
daca
daca si numai
daca ![]()
este element neutru atat la stanga cat si la dreapta .

![]() Exercitiul nr. 1 : ( Ganga )
Exercitiul nr. 1 : ( Ganga )
Pe multimea ![]() definim aplicatia
definim aplicatia ![]() :
: ![]() .
.
Sa se arate ca ![]() este o lege de
compozitie pe
este o lege de
compozitie pe ![]() . cu element
neutru .
. cu element
neutru .
![]() Exercitiul nr. 2 : ( Ganga )
Exercitiul nr. 2 : ( Ganga )
Pe multimea ![]() se considera
aplicatia :
se considera
aplicatia : ![]() . Aratati ca
. Aratati ca ![]() este o structura
algebrica fara element neutru .
este o structura
algebrica fara element neutru .
![]() Exercitiul nr. 3 : ( Ganga )
Exercitiul nr. 3 : ( Ganga )
Pe multimea ![]() definim
aplicatia :
definim
aplicatia : ![]() .
.
Aratati ca ![]() este o structura
algebrica avand elementul neutru
este o structura
algebrica avand elementul neutru ![]() .
.
![]() Exercitiul nr. 4 : ( Ganga )
Exercitiul nr. 4 : ( Ganga )
Fie ![]() o submultime a
lui
o submultime a
lui ![]() . Definim pe
. Definim pe ![]() legea de
compozitie :
legea de
compozitie :
![]()
Aratati ca ![]() este o structura algebrica
cu elementul neutru
este o structura algebrica
cu elementul neutru ![]() .
.
![]() Exercitiul nr. 5 : ( Schneider )
Exercitiul nr. 5 : ( Schneider )
Sa se calculeze elementul neutru fata de legea :
a). ![]() pe
pe ![]() ;
;
b). 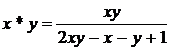 pe
pe ![]() ;
;
c). 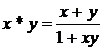 pe
pe ![]() ;
;
d). ![]() pe
pe ![]()
e). ![]() pe
pe ![]() .
.
![]() Exercitiul nr. 6 : ( Schneider )
Exercitiul nr. 6 : ( Schneider )
Sa se arate ca nu exista element neutru fata de legea :
a). 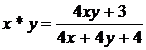 pe
pe 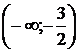 ;
;
b). ![]() pe
pe ![]() .
.
![]()

P
Vom
considera structura algebrica ![]()
adica ![]() o multime nevida
echipata cu o lege de compozitie
o multime nevida
echipata cu o lege de compozitie ![]() :
:
![]() ,
, ![]() .
.
P
Vom
presupune in plus ca aceasta lege de compozitie este asociativa si ca admite
element neutru , fie acesta ![]() .
.
Definitie ELEMENT SIMETRIZABIL :
Un
element ![]() se numeste simetrizabil in raport cu o lege de compozitie
se numeste simetrizabil in raport cu o lege de compozitie
![]() ,
, ![]() , asociativa si cu element neutru , daca exista un element :
, asociativa si cu element neutru , daca exista un element :
![]() astfel incat
astfel incat ![]() ,
, ![]()
Observatii Element Simetrizabil :
1). Daca ![]() este simetrizabil , atunci unicul element
este simetrizabil , atunci unicul element ![]() cu proprietatea :
cu proprietatea :
![]()
se numeste simetricul lui ![]() ( in
raport cu operatia
( in
raport cu operatia ![]() ) .
) .
2). Facem precizarea si in acest caz ca simetricul lui ![]() , elementul
, elementul ![]() trebuie sa
trebuie sa
apartina multimii
![]() .
.
Definitie ELEMENT SIMETRIC la stanga :
- Fie ![]() o operatie algebrica avand
o operatie algebrica avand ![]() element neutru la stanga si
element neutru la stanga si ![]() .
.
Spunem ca ![]() este un simetric al lui
este un simetric al lui ![]() la stanga in raport cu
legea
la stanga in raport cu
legea ![]() daca :
daca :
![]()
Se
mai spune ca ![]() este simetrizabil la stanga in raport cu
este simetrizabil la stanga in raport cu ![]() daca exista
daca exista
![]() pentru
care :
pentru
care :
![]() .
.
Definitie ELEMENT SIMETRIC la dreapta :
- Fie ![]() o operatie algebrica avand
o operatie algebrica avand ![]() element neutru la stanga si
element neutru la stanga si ![]() .
.
Spunem ca ![]() este un simetric al lui
este un simetric al lui ![]() la dreapta in raport cu
legea
la dreapta in raport cu
legea ![]() daca :
daca :
![]()
- Se mai spune ca ![]() este simetrizabil la dreapta in raport cu
este simetrizabil la dreapta in raport cu ![]() daca exista
daca exista ![]() pentru care :
pentru care :
![]() .
.
TEOREMA :
- Fie ![]() o operatie algebrica asociativa si cu element neutru
o operatie algebrica asociativa si cu element neutru ![]() . Daca
. Daca ![]() are un element simetric , atunci acesta este
unic .
are un element simetric , atunci acesta este
unic .
TEOREMA :
- Fie ![]() o operatie algebrica asociativa si cu element neutru . Atunci :
o operatie algebrica asociativa si cu element neutru . Atunci :
1). Daca elementele ![]() sunt simetrizabile , atunci compusul lui
sunt simetrizabile , atunci compusul lui ![]() cu
cu ![]() este simetrizabil si mai mult :
este simetrizabil si mai mult :
![]()
2). Daca elemntul ![]() este
simetrizabil , simetricul sau ,
este
simetrizabil , simetricul sau , ![]() , este de asemenea
, este de asemenea
simetrizabil si :
![]()
3). Daca ![]() este simetrizabil , iar
este simetrizabil , iar ![]() nu este simetrizabil , atunci :
nu este simetrizabil , atunci :
![]()
nu sunt simetrizabile .

![]() Exercitiul
nr. 1 : ( Schneider )
Exercitiul
nr. 1 : ( Schneider )
Sa se studieze simetrizabilitatea elementelor urmatoarelor multimi in raport cu legile de compozitie specificate :
a). ![]() ;
; ![]() ;
;
b). ![]() ;
; ![]() ;
;
c). ![]() ;
; ![]() ;
;
d). ![]() ;
; ![]() ;
;
e). ![]() ;
; ![]() ;
;
f). ![]() ;
; 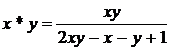 ;
;
g). ![]() ;
; ![]() .
.
![]() Exercitiul
nr. 2 : ( Ganga )
Exercitiul
nr. 2 : ( Ganga )
Pe multimea ![]() definim
aplicatia
definim
aplicatia ![]() :
: ![]() .
.
Sa se arate ca ![]() este o lege de
compozitie pe
este o lege de
compozitie pe ![]() . cu element
neutru . Determinati
. cu element
neutru . Determinati
elementele simetrizabile din ![]() in raport cu
legea
in raport cu
legea ![]() .
.
![]() Exercitiul
nr. 3 : ( Ganga )
Exercitiul
nr. 3 : ( Ganga )
Pe multimea ![]() definim
aplicatia :
definim
aplicatia : ![]() .
.
Aratati ca ![]() este o structura
algebrica avand elementul neutru
este o structura
algebrica avand elementul neutru ![]() . Determinati
. Determinati
elementele simetrizabile din ![]() in raport cu
legea
in raport cu
legea ![]() .
.


P
Fie ![]() un numar intreg ;
un numar intreg ;
P
Daca ![]() am definit :
am definit :
Definitie Suma modulo n :
- Definim suma modulo ![]() a lui
a lui ![]() cu
cu ![]() , notata cu :
, notata cu : ![]() ca fiind restul impartirii prin
ca fiind restul impartirii prin ![]() al numarului
al numarului ![]() :
:
![]()
Definitie Produsul modulo n :
- Definim produsul modulo
![]() a lui
a lui ![]() cu
cu ![]() , notata cu :
, notata cu : ![]() ca fiind restul impartirii prin
ca fiind restul impartirii prin ![]() al numarului
al numarului ![]() :
:
![]()
P
S-au
obtinut astfel doua legi de compozitie pe ![]() :
:
1). ![]() ,
, ![]()
si
2). ![]() ,
, ![]()
numite adunarea modulo ![]() , respectiv inmultirea modulo
, respectiv inmultirea modulo ![]() .
.
Observatii :
1). Vom nota cu ![]() multimea claselor modulo
multimea claselor modulo ![]() :
: ![]()
Exemplu : ![]() sau
sau ![]() etc.
etc.
Lema :
- Fie ![]() ;
;
- Atunci oricare ar fi ![]() avem : 1).
avem : 1). ![]()
si
2). ![]() .
.
TEOREMA :
Operatiile de
adunare si inmultire modulo ![]() au proprietatile :
au proprietatile :
1). ![]() ;
;
2). ![]() ;
;
3). ![]() ;
;
4). ![]() ;
;
5). ![]()
oricare ar fi ![]() .
.
Observatii :
Operatia " ![]() " are prioritate fata de "
" are prioritate fata de " ![]() " si de aceea intr-o expresie ca :
" si de aceea intr-o expresie ca :
![]()
parantezele pot fi omise , scriind simplu :
![]()

![]() Exercitiul
nr. 1 : ( Manual )
Exercitiul
nr. 1 : ( Manual )
Sa se alcatuiasca tablele operatiilor
induse pe ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() de adunarea si
inmultirea modulo
de adunarea si
inmultirea modulo ![]() .
.
![]() Exercitiul
nr. 2 : ( Manual )
Exercitiul
nr. 2 : ( Manual )
Pe ![]() definim legea de
compozitie
definim legea de
compozitie ![]() ,
, ![]() , unde :
, unde :
![]() . Aratati ca aceasta
lege de compozitie este asociativa , comutativa si cu element neutru .
Intervalul
. Aratati ca aceasta
lege de compozitie este asociativa , comutativa si cu element neutru .
Intervalul ![]() este parte stabila a
lui
este parte stabila a
lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() ?
?
![]() Exercitiul
nr. 3 : ( Manual )
Exercitiul
nr. 3 : ( Manual )
Pe ![]() definim legea de
compozitie
definim legea de
compozitie ![]() . Fie
. Fie ![]() . Aratati ca
. Aratati ca ![]() este o structura
algebrica comutativa , cu element neutru si ca orice element din
este o structura
algebrica comutativa , cu element neutru si ca orice element din ![]() este simetrizabil in
raport cu legea
este simetrizabil in
raport cu legea ![]() .
.
![]() Exercitiul
nr. 4 : ( Manual )
Exercitiul
nr. 4 : ( Manual )
Fie ![]() si aplicatia :
si aplicatia : 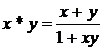 . Aratati ca
. Aratati ca ![]() este o structura
algebrica asociativa , comutativa , cu element neutru si orice element din
este o structura
algebrica asociativa , comutativa , cu element neutru si orice element din ![]() este simetrizabil in
raport cu
este simetrizabil in
raport cu ![]() .
.
![]() Exercitiul
nr. 5 : ( Manual )
Exercitiul
nr. 5 : ( Manual )
Se considera ![]() si aplicatia :
si aplicatia : ![]() . Aratati ca
. Aratati ca ![]() este o
este o
structura
algebrica asociativa , comutativa , cu element neutru si ca orice element
din ![]()
este simetrizabil in raport cu legea data .
![]() Exercitiul
nr. 6 : ( Manual )
Exercitiul
nr. 6 : ( Manual )
Fie ![]() si aplicatia :
si aplicatia : 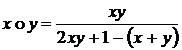 . Aratati ca
. Aratati ca ![]() este o
este o
structura
algebrica asociativa , comutativa , cu element neutru si ca orice element
din ![]()
este simetrizabil in raport cu legea data .
![]() Exercitiul
nr. 7 : ( Manual )
Exercitiul
nr. 7 : ( Manual )
Gasiti toate solutiile
din ![]() ale sistemului de
ecuatii liniare :
ale sistemului de
ecuatii liniare :
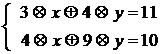 .
.
![]() Exercitiul
nr. 8 : ( Manual )
Exercitiul
nr. 8 : ( Manual )
Pe ![]() definim legea de compozitie
definim legea de compozitie ![]() ,
, ![]() , unde :
, unde :
![]() . Aratati ca aceasta
lege de compozitie este asociativa , comutativa si cu element neutru . Sa se
determine elementele simetrizabile .
. Aratati ca aceasta
lege de compozitie este asociativa , comutativa si cu element neutru . Sa se
determine elementele simetrizabile .
![]() Exercitiul
nr. 9 : ( Nastasescu )
Exercitiul
nr. 9 : ( Nastasescu )
Pe multimea ![]() a numerelor reale
definim legea de compozitie
a numerelor reale
definim legea de compozitie ![]() astfel :
astfel :
![]() , oricare ar fi
, oricare ar fi ![]() . Sa se arate ca
aceasta lege de compozitie este asociativa , comutativa si cu element neutru .
Sa se determine elementele simetrizabile .
. Sa se arate ca
aceasta lege de compozitie este asociativa , comutativa si cu element neutru .
Sa se determine elementele simetrizabile .
![]() Exercitiul
nr. 10 : ( Gil )
Exercitiul
nr. 10 : ( Gil )
Fie ![]() si legea
si legea ![]() definita pe
definita pe ![]() prin :
prin : ![]() ,
, ![]() ,
, ![]() . Atunci
. Atunci ![]() este lege de
compozitie pe
este lege de
compozitie pe ![]() daca si numai
daca
daca si numai
daca ![]()
![]() Exercitiul
nr. 11 : ( Gil )
Exercitiul
nr. 11 : ( Gil )
Legea de compozitie ![]() ,
, ![]() ,
, ![]() . Atunci
. Atunci ![]() este lege de
compozitie comutativa daca si numai daca
este lege de
compozitie comutativa daca si numai daca ![]()
![]() Exercitiul
nr. 12 : ( Gil )
Exercitiul
nr. 12 : ( Gil )
Legea de compozitie ![]() ,
, ![]() ,
, ![]() . Atunci
. Atunci ![]() este lege de
compozitie asociativa daca si numai daca
este lege de
compozitie asociativa daca si numai daca ![]()
![]() Exercitiul
nr. 13 : ( Gil )
Exercitiul
nr. 13 : ( Gil )
Elementul neutru al legii de compozitie ![]() ,
, ![]() este ?
este ?
![]() Exercitiul
nr. 14 : ( Gil )
Exercitiul
nr. 14 : ( Gil )
Fie ![]() si legea
si legea ![]() definita pe
definita pe ![]() prin :
prin :
![]() ,
, ![]() .
.
Aratati ca ![]() este o lege de
compozitie pe
este o lege de
compozitie pe ![]() .
.
![]() Exercitiul
nr. 15 : ( Gil )
Exercitiul
nr. 15 : ( Gil )
Fie ![]() si
si 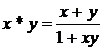 ,
, ![]() . Aratati ca
. Aratati ca ![]() este lege de
compozitie pe
este lege de
compozitie pe ![]() .
.
![]() Exercitiul
nr. 16 : ( Gil )
Exercitiul
nr. 16 : ( Gil )
Sa se arate ca legea de compozitie : ![]() ,
, ![]() .
.
a). Nu este comutativa ;
b). Nu este asociativa .
![]() Exercitiul
nr. 17 : ( Gil )
Exercitiul
nr. 17 : ( Gil )
Sa se arate ca legea de compozitie : ![]() ,
, ![]() nu admite element
neutru .
nu admite element
neutru .
![]() Exercitiul
nr. 18 : ( Gil )
Exercitiul
nr. 18 : ( Gil )
Sa se determine elementele
simetrizabile din multimea ![]() in raport cu
legea :
in raport cu
legea :
![]() ,
, ![]()
![]() Exercitiul
nr. 19 : ( Gil )
Exercitiul
nr. 19 : ( Gil )
Fie ![]() . Pe
. Pe ![]() definim legea de
compozitie
definim legea de
compozitie ![]() astfel :
astfel : ![]()
![]()
Sa se determine ![]() astfel incat aceasta
lege de compozitie sa fie asociativa si comutativa .
astfel incat aceasta
lege de compozitie sa fie asociativa si comutativa .
![]() Exercitiul
nr. 20 : ( Gil )
Exercitiul
nr. 20 : ( Gil )
Se considera multimea numerelor
reale ![]() pe care se defineste
legea de compozitie :
pe care se defineste
legea de compozitie :
![]() ,
, ![]()
a). Sa se arate ca legea ![]() este asociativa si
comutativa .
este asociativa si
comutativa .
b). Sa se determine elementul neutru al legii ![]() .
.
c). Sa se arate ca : ![]() ,
, ![]() .
.
d). Sa se arate ca multimea ![]() este parte stabila in
raport cu legea
este parte stabila in
raport cu legea ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |