
Ecuatii diferentiale de ordinal intai
Fie ![]() un interval marginit
sau nemarginit al axei reale si domeniul deschis
un interval marginit
sau nemarginit al axei reale si domeniul deschis ![]() ,
, ![]() . Consideram functia
. Consideram functia ![]() ,
, ![]() , de clasa
, de clasa ![]() si notam cu
si notam cu ![]() ,
, ![]() derivata functiei
derivata functiei
![]() pe
pe ![]() .
.
Fiind data functia
![]() ,
, ![]() apartinand unei
anumite clase de regularitate pe
apartinand unei
anumite clase de regularitate pe ![]() (de exemplu,
(de exemplu, ![]() ), spunem ca relatia (functionala)
), spunem ca relatia (functionala)
![]()
![]() , (1.1)
, (1.1)
defineste o ecuatie diferentiala de ordinal intai sub forma implicita.
Definitie Se
numeste solutie, pe intervalul ![]() , a ecuatiei
diferentiale (1.1) o functie
, a ecuatiei
diferentiale (1.1) o functie ![]() , de clasa
, de clasa ![]() care verifica
conditiile
care verifica
conditiile
![]() (1.2)
(1.2)
In multe situatii, in locul ecuatiei
diferentiale implicite (1.1), se poate considera ecuatia
diferentiala explicitata in raport cu derivata
![]() . Fie functia
. Fie functia ![]() , in general continua pe
, in general continua pe ![]() . Atunci consideram ecuatia
diferentiala de ordinal intai sub forma normala (forma standard)
. Atunci consideram ecuatia
diferentiala de ordinal intai sub forma normala (forma standard)
![]()
![]() , (1.3)
, (1.3)
Definitie Fiind data functia
![]() , spunem ca functia
, spunem ca functia
![]() , se numeste
solutie, pe
, se numeste
solutie, pe ![]() , a ecuatiei diferentiale sub forma
normala (1.3), daca
, a ecuatiei diferentiale sub forma
normala (1.3), daca ![]() este derivabila
pe intervalul
este derivabila
pe intervalul ![]() si verifica conditiile
si verifica conditiile
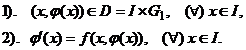 (1.4)
(1.4)
Este evident ca prima conditie
(1.4) arata ca graficul functiei ![]() , este inclus in produsul cartezian
, este inclus in produsul cartezian ![]() . Asadar, datorita conditiei (1.4)1
retinem incluziunea de multimi
. Asadar, datorita conditiei (1.4)1
retinem incluziunea de multimi
![]() ,
,
In consecinta, identitatea (1.4)2
este bine definita in toate punctele ![]() si asa cum
vom vedea, in toate punctele multimii
si asa cum
vom vedea, in toate punctele multimii ![]() .
.
Observatia Ecuatia diferentiala scrisa
sub forma normala (1.3) arata ca in structura acesteia, pe de o
parte, intra variabila
independenta ![]() cat si variabila dependenta
cat si variabila dependenta ![]() , care adesea este numita functie
necunoscuta, iar pe de alta parte functia
, care adesea este numita functie
necunoscuta, iar pe de alta parte functia ![]() , numita camp
vectorial (camp de vectori). Daca variabila dependenta (functia necunoscuta)
depinde de o singura variabila spunem ca relatia (1.3), respectiv
(1.1), defineste o ecuatie
diferentiala ordinara. In cazul
cand functia necunoscuta depinde de mai multe variabile independente
ecuatia se numeste ecuatie
diferentiala cu derivate partiale.
, numita camp
vectorial (camp de vectori). Daca variabila dependenta (functia necunoscuta)
depinde de o singura variabila spunem ca relatia (1.3), respectiv
(1.1), defineste o ecuatie
diferentiala ordinara. In cazul
cand functia necunoscuta depinde de mai multe variabile independente
ecuatia se numeste ecuatie
diferentiala cu derivate partiale.
Ordinul unei
ecuatii diferentiale este dat de ordinul cel
mai mare "![]() " de derivare al variabilei dependente care intra in
expresia ecuatiei diferentiale.
" de derivare al variabilei dependente care intra in
expresia ecuatiei diferentiale.
Observatia Folosind diferite notatii pentru
derivata variabilei dependente ![]() , atunci ecuatia diferentiala sub forma
normala (1.3) poate fi scrisa sub formele echivalente
, atunci ecuatia diferentiala sub forma
normala (1.3) poate fi scrisa sub formele echivalente
![]() sau
sau ![]() sau
sau ![]() , (1.3')
, (1.3')
iar, cand in locul variabilei independente ![]() folosim variabila
temporala
folosim variabila
temporala ![]() , vom scrie
, vom scrie
![]() sau
sau ![]() sau
sau ![]() . (1.3')
. (1.3')
Observatia Daca, referitor la o baza
aleasa in ![]() , se da un sistem de coordonate pe
, se da un sistem de coordonate pe ![]() , atunci functiile
, atunci functiile ![]() , si
, si ![]() , pot fi scrise unic pe componente prin formulele
, pot fi scrise unic pe componente prin formulele
![]() , respectiv
, respectiv ![]() .
.
In acest caz, dupa identificari, ecuatia
diferentiala normala (1.3), se scrie cu ajutorul unui sistem de ![]() ecuatii
diferentiale de ordinal intai, pentru componentele
ecuatii
diferentiale de ordinal intai, pentru componentele ![]() , considerate ca variabile dependente (functii
necunoscute), sub forma echivalenta
, considerate ca variabile dependente (functii
necunoscute), sub forma echivalenta
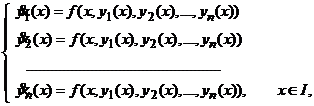 (1.5)
(1.5)
iar functia derivabila ![]() , solutie a acestui system, are forma
, solutie a acestui system, are forma
![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |