
Au forma generala
![]() ;
;![]() , (3.1)
, (3.1)
unde ![]() sunt functii
continue care depind numai de variabila independenta
sunt functii
continue care depind numai de variabila independenta ![]() ,
, ![]() ( x I I si
( x I I si  reprezinta datele
initiale.
reprezinta datele
initiale.
Vom analiza cazurile particulare
i). Daca ![]() , atunci ecuatia diferentiala
obtinuta
, atunci ecuatia diferentiala
obtinuta
![]() , (3.2)
, (3.2)
se numeste ecuatia lineara si omogena asociata ecuatiei (3.1). Aceasta ecuatie constituie un caz particular de ecuatie cu variabile separabile.
Proprietatea de existenta si
unicitate a solutiilor
ecuatiei (3.2) afirma ca, daca functia  este continua pe
este continua pe ![]() , atunci pentru orice punct
, atunci pentru orice punct  exista si
este unica functia
exista si
este unica functia ![]() , solutie a ecuatiei (3.2) care trece prin
, solutie a ecuatiei (3.2) care trece prin ![]() si are forma
si are forma
![]() (
( ![]() (3.3)
(3.3)
Prin ![]() intelegem
functia care depinde de variabila independenta
intelegem
functia care depinde de variabila independenta ![]() si care in
punctul
si care in
punctul ![]() ia valoarea
ia valoarea ![]() si notam
si notam ![]() .
.
Intr-adevar,
cu notatia  , ecuatia (3.2) devine
, ecuatia (3.2) devine
![]() ,
, ![]() (3.4)
(3.4)
si
atunci ![]() este continua
si are derivata partiala
este continua
si are derivata partiala ![]() continua.
Potrivit teoremei de existenta si unicitate, problema Cauchy
admite o solutie unica in orice punct
continua.
Potrivit teoremei de existenta si unicitate, problema Cauchy
admite o solutie unica in orice punct  . Pentru a determina solutia generala a
ecuatiei (3.4) distingem cazurile:
. Pentru a determina solutia generala a
ecuatiei (3.4) distingem cazurile:
a). Daca ![]() atunci functia
atunci functia ![]() (
( ![]() este o solutie stationara
a ecuatiei (3.4).
este o solutie stationara
a ecuatiei (3.4).
b). Daca ![]() atunci prin separarea
variabilelor din (3.4) putem scrie
atunci prin separarea
variabilelor din (3.4) putem scrie
![]() ,
, ![]() , (3.5)
, (3.5)
apoi se determina cate o primitiva in fiecare membru al ecuatiei (3.5). Rezulta
![]() ,
, ![]() , (3.6)
, (3.6)
unde s-a ales ![]() . Din (3.6) obtinem solutia
generala a ecuatiei lineare omogena asociata sub forma
. Din (3.6) obtinem solutia
generala a ecuatiei lineare omogena asociata sub forma
![]() ,
, ![]() (3.7)
(3.7)
Vom observa
ca, daca ![]() intr-un punct
intr-un punct ![]() , atunci din (3.7), luand c
= 0, regasim solutia stationara
, atunci din (3.7), luand c
= 0, regasim solutia stationara ![]() . Asadar,
. Asadar, ![]() este solutie particulara a
ecuatiei lineare si omogene asociate.
este solutie particulara a
ecuatiei lineare si omogene asociate.
In
consecinta, familia
solutiilor (3.7) impreuna cu solutia
stationara ![]() (numita solutie
particulara pentru ca se poate obtine din solutia
generala prin particularizarea constantei (se alege c = 0)) formeaza solutia
generala a ecuatiei lineare si omogene asociate (3.2)
si are forma
(numita solutie
particulara pentru ca se poate obtine din solutia
generala prin particularizarea constantei (se alege c = 0)) formeaza solutia
generala a ecuatiei lineare si omogene asociate (3.2)
si are forma
 . (3.8)
. (3.8)
Ecuatia diferentiala
lineara omogena de ordinul intai nu are solutii singulare, ea
are numai o solutie particulara ![]() ,
, ![]() .
.
Observatie. Deoarece, prin calcul direct, am stabilit
formula pentru solutia generala
a ecuatiei (3.2), evident in ipoteza continuitatii functiei
![]() , atunci putem afirma ca problema Cauchy pentru
ecuatia (3.2) are o unica solutie.
, atunci putem afirma ca problema Cauchy pentru
ecuatia (3.2) are o unica solutie.
Datorita
liniaritatii ecuatiei omogene ![]() , putem afirma ca multimea solutiilor maximale ale acestei ecuatii,
, putem afirma ca multimea solutiilor maximale ale acestei ecuatii,
![]()
formeaza un spatiu vectorial. Rezultatul acesta important este dat de urmatoarea
Teorema. Solutiile
maximale ale ecuatiei lineare si omogene (3.2) formeaza un spatiu vectorial de
dimensiune ![]() , in care putem alege ca baza functia
, in care putem alege ca baza functia 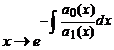 .
.
Observatie. Ecuatia diferentiala (3.1) se mai numeste ecuatie diferentiala afina (scalara) sau ecuatie diferentiala lineara si neomogena.
ii) Un caz particular interesant este acela in care ![]() si
si ![]() ( )
( )![]() .
.
Atunci, ecuatia diferentiala lineara neomogena poate fi scrisa sub forma
![]() . (3.9)
. (3.9)
Solutia
ecuatiei (3.9), care verifica conditia initiala ![]() , se obtine prin cuadraturi si avem
, se obtine prin cuadraturi si avem
![]()
![]() ,
,
sau
![]() ,
, ![]() .
.
Tinand cont
ca ![]() ( )
( ) ![]() , din ultima relatie obtinem solutia problemei
Cauchy (3.1) sub forma explicita
, din ultima relatie obtinem solutia problemei
Cauchy (3.1) sub forma explicita
![]() ,
, ![]() . (3.10)
. (3.10)
Pentru integrarea ecuatiei diferentiale (3.1) vom folosi metoda factorului integrant. In acest scop se scrie ecuatia diferentiala lineara neomogena (3.1) sub forma normala
![]() , (3.11)
, (3.11)
unde ![]() sunt functii
continue care depind numai de variabila independenta
sunt functii
continue care depind numai de variabila independenta ![]() , definite prin
, definite prin 
![]()
![]()
![]() .
.
Punctele
![]() pentru care
pentru care ![]() sunt numite puncte singulare ale ecuatiei
diferentiale sub forma normala. In aceste puncte singulare
existenta si unicitatea solutiei nu mai este asigurata.
sunt numite puncte singulare ale ecuatiei
diferentiale sub forma normala. In aceste puncte singulare
existenta si unicitatea solutiei nu mai este asigurata.
In continuare, prin
calcul direct, vom arata ca solutia
problemei Cauchy asociata ecuatiei diferentiale lineare de
ordinul intai este unic determinata. Mai precis, pentru orice ![]() exista o
unica functie
exista o
unica functie ![]() care verifica
ecuatia diferentiala sub forma normala (3.11) si
conditia initiala data (adica,
care verifica
ecuatia diferentiala sub forma normala (3.11) si
conditia initiala data (adica, ![]() ,
,![]() ).
).
Privind cu
atentie cazul ii) constatam
ca metoda folosita la determinarea solutiei sugereaza
existenta unei functii ![]() ,
, ![]() , numita factor
integrant, astfel incat dupa inmultirea ecuatiei diferentiale
(3.11) cu
, numita factor
integrant, astfel incat dupa inmultirea ecuatiei diferentiale
(3.11) cu ![]() sa o transforme
intr-o ecuatie "usor
integrabila"
sa o transforme
intr-o ecuatie "usor
integrabila"
![]() (3.12)
(3.12)
Pentru aceasta vom scrie
membrul stang al ecuatiei (3.12) cu ajutorul derivatei produsului ![]() . Avem
. Avem
![]() .
.
Evident, pentru ca aceasta egalitate sa aiba loc oricare ar fi x I I, trebuie sa se verifice conditia
![]() ,
, ![]() . (3.13)
. (3.13)
Din ultima relatie (3.13), calculand in fiecare membru cate o primitiva, deducem
![]() ,
, ![]() ,
,
sau sub forma echivalenta
![]() ,
, ![]() (3.14)
(3.14)
Deoarece functia
![]() este continua
este continua ![]() , rezulta ca
, rezulta ca ![]() ,
, ![]() , este functie continua si, cum membrul drept
al relatiei (3.14) este strict pozitiv, rezulta ca
, este functie continua si, cum membrul drept
al relatiei (3.14) este strict pozitiv, rezulta ca ![]()
![]() . Asadar, factorul integrant are expresia
. Asadar, factorul integrant are expresia
![]() , unde
, unde ![]() ,
, ![]() . (3.15)
. (3.15)
Vom observa ca
in calculele finale ![]() nu intervine, asa
ca valoarea ei poate fi aleasa egala cu 1. Avem
nu intervine, asa
ca valoarea ei poate fi aleasa egala cu 1. Avem
![]() (3.16)
(3.16)
Odata cu alegerea factorului integrant sub forma (3.16), deducem ca ecuatia (3.12) poate fi scrisa sub forma
![]() (3.17)
(3.17)
Luand primitivele in ambii membri ai ecuatiei (3.17), rezulta
![]() .
.
Deoarece ![]() nu apare explicit in
calcule putem alege
nu apare explicit in
calcule putem alege ![]() . Atunci ultima relatie arata ca solutia
problemei Cauchy (3.1) se poate scrie sub forma
. Atunci ultima relatie arata ca solutia
problemei Cauchy (3.1) se poate scrie sub forma
![]() (3.18)
(3.18)
Este usor de vazut ca din ecuatia (3.17), prin cuadraturi, deducem solutia generala a ecuatiei lineare neomogene (3.1) sub forma
![]() ,
, ![]() , (3.19)
, (3.19)
sau, daca tinem seama de expresia factorului integrant (3.16), putem scrie solutia generala sub forma echivalenta
![]() ,
, ![]() (3.20)
(3.20)
Din expresia solutiei (3.20) observam modul sub care intra coeficientii ecuatiei diferentiale, pusa sub forma normala (3.11), in structura solutiei generale.
Urmarind rationamentul de mai sus, putem considera urmatorul algoritm folosit in obtinerea solutiei generale:
Pasul 1. Se scrie ecuatia lineara neomogena sub forma normala (canonica)
![]() .
.
Pasul 2. Se determina factorul integrant ![]() .
.
Pasul 3. Se multiplica ecuatia neomogena cu factorul integrant ![]() , si avem
, si avem

Pasul 4. Se integreaza ultima relatie si se obtine solutia generala.
Mentionam
ca ecuatia lineara omogena de ordinul intai nu are
solutii singulare, ea are numai o solutie particulara ![]() ,
, ![]() .
.
Ecuatia
diferentiala (3.1) poate avea solutii
singulare de forma ![]() , unde
, unde ![]() este
radacina ecuatiei
este
radacina ecuatiei ![]() .
.
Observatie. Pentru determinarea solutiei generale a ecuatiei diferentiale (3.1), se poate folosi metoda variatiei constantelor (sau metoda lui Lagrange[1]). In acest scop, presupunem ca ecuatia diferentiala (3.1) este scrisa sub forma normala (3.11). Structura solutiei generale sub forma (3.20) arata ca aceasta se obtine cu ajutorul solutiei generale a ecuatiei lineare omogene asociate
![]() , (3.21)
, (3.21)
la care se aduna o solutie particulara a ecuatiei lineare neomogene pusa sub forma normala (3.11).
Intr-adevar,
fie ![]() solutia generala a ecuatiei diferentiale
normale (3.11) si
solutia generala a ecuatiei diferentiale
normale (3.11) si ![]() o solutie
particulara a aceleiasi ecuatii diferentiale. Atunci
functia
o solutie
particulara a aceleiasi ecuatii diferentiale. Atunci
functia ![]() verifica ecuatia
lineara omogena (3.21),
asociata ecuatiei neomogene (3.11). Asadar, daca se
cunoaste o solutie particulara
verifica ecuatia
lineara omogena (3.21),
asociata ecuatiei neomogene (3.11). Asadar, daca se
cunoaste o solutie particulara ![]() a ecuatiei
neomogene (3.11) si solutia generala
a ecuatiei
neomogene (3.11) si solutia generala ![]() a ecuatiei
omogene (3.21), atunci
a ecuatiei
omogene (3.21), atunci ![]() reprezinta
solutia generala a ecuatiei neomogene (3.11).
reprezinta
solutia generala a ecuatiei neomogene (3.11).
Vom observa ca
ecuatia diferentiala omogena (3.21) este cu variabile
separabile si pentru ![]() , dupa separarea variabilelor, conduce la solutia
generala
, dupa separarea variabilelor, conduce la solutia
generala
![]() ,
, ![]() . (3.22)
. (3.22)
Pentru a determina
o solutie particulara ![]() , a ecuatiei neomogene (3.11), introducem, odata cu
Lagrange, functia
, a ecuatiei neomogene (3.11), introducem, odata cu
Lagrange, functia ![]() definita prin
definita prin
![]() ,
, ![]() , (3.23)
, (3.23)
unde ![]() este o solutie
oarecare a ecuatiei lineare neomogene (3.11), deci verifica
ecuatia diferentiala neomogena sub forma normala
este o solutie
oarecare a ecuatiei lineare neomogene (3.11), deci verifica
ecuatia diferentiala neomogena sub forma normala
![]() ,
, ![]() . (3.24)
. (3.24)
Din (3.23) deducem
ca functia ![]() este derivabila
si scriind relatia (3.23) sub forma echivalenta
este derivabila
si scriind relatia (3.23) sub forma echivalenta
![]() , (3.25)
, (3.25)
observam ca am considerat, de fapt, solutia generala a ecuatiei omogene (3.21).
Inlocuind expresia
(3.25) in ecuatia (3.24), rezulta ca functia ![]() verifica
ecuatia diferentiala
verifica
ecuatia diferentiala
![]() .
.
Din ultima
ecuatie, prin integrare, deducem ca functia ![]() are expresia
are expresia
![]() (3.26)
(3.26)
si atunci solutia ![]() are forma
are forma
![]() (3.27)
(3.27)
Reciproc, orice functie de forma (3.27) este o solutie a ecuatiei diferentiale lineare neomogene.
Metoda
folosita se numeste metoda variatiei constantelor (sau
metoda lui Lagrange) intrucat relatia (3.25) arata ca expresia
unei solutii oarecare a ecuatiei neomogene se obtine din
solutia ecuatiei omogene (3.22), inlocuind constanta c cu o functie oarecare ![]() .
.
Observatie.
Functia ![]() , introdusa prin relatia (3.23), asa dupa
cum s-a vazut, verifica ecuatia diferentiala
, introdusa prin relatia (3.23), asa dupa
cum s-a vazut, verifica ecuatia diferentiala
![]()
si atunci functia ![]() este o primitiva
a functiei cunoscute
este o primitiva
a functiei cunoscute ![]() . Solutia ecuatiei omogene are forma
. Solutia ecuatiei omogene are forma ![]() ,
, ![]() , sau
, sau ![]() , unde
, unde ![]() este o primitiva
a functiei
este o primitiva
a functiei ![]() .
.
Dupa cum se constata, solutia ecuatiei neomogene
![]() , (*)
, (*)
are aceeasi forma cu cea a
ecuatiei omogene, numai ca functia ![]() este primitiva a
functiei cunoscute
este primitiva a
functiei cunoscute ![]() . Aceasta asemanare, ca forma, a celor
doua solutii l-a condus pe Lagrange la un procedeu foarte simplu de
determinare a solutiei ecuatiei neomogene, procedeu cunoscut sub numele
de metoda variatiei constantelor.
. Aceasta asemanare, ca forma, a celor
doua solutii l-a condus pe Lagrange la un procedeu foarte simplu de
determinare a solutiei ecuatiei neomogene, procedeu cunoscut sub numele
de metoda variatiei constantelor.
Daca
notam cu ![]() solutia
ecuatiei omogene, care in punctul
solutia
ecuatiei omogene, care in punctul ![]() ia valoarea
ia valoarea ![]() (adica, solutia
problemei Cauchy pentru ecuatia omogena), atunci putem scrie
(adica, solutia
problemei Cauchy pentru ecuatia omogena), atunci putem scrie
![]() .
.
Folosind aceasta
notatie cat si expresia (*) deducem ca o solutie particulara ![]() a ecuatiei
neomogene, care se anuleaza in
a ecuatiei
neomogene, care se anuleaza in ![]() , are forma
, are forma
![]() (*
(*
unde ![]() este solutia
ecuatiei omogene care in punctul
este solutia
ecuatiei omogene care in punctul ![]() ia valoarea
ia valoarea ![]() , data de termenul liber. Relatia ( *) constituie principiul lui Duhamel
pentru ecuatiile diferentiale lineare sau ecuatiile
diferentiale lineare cu derivate partiale.
, data de termenul liber. Relatia ( *) constituie principiul lui Duhamel
pentru ecuatiile diferentiale lineare sau ecuatiile
diferentiale lineare cu derivate partiale.
Observatie.
Ecuatia diferentiala (3.11) se poate integra folosind metoda
lui Bernoulli, care consta in schimbarea de functie ![]() , unde
, unde ![]() si
si ![]() sunt doua
functii derivabile, deocamdata necunoscute. Substituind in
ecuatia diferentiala (3.11) avem
sunt doua
functii derivabile, deocamdata necunoscute. Substituind in
ecuatia diferentiala (3.11) avem
![]() sau
sau ![]() .
.
Observam
ca una din functii, de exemplu, functia ![]() se poate
determina din conditia
(coeficientul lui
se poate
determina din conditia
(coeficientul lui ![]() sa fie nul)
sa fie nul) ![]() si are forma
si are forma ![]() . Rezulta ca
. Rezulta ca ![]() trebuie sa
verifice ecuatia diferentiala
trebuie sa
verifice ecuatia diferentiala
![]() sau
sau ![]() ,
,
de unde obtinem
![]() ,
, ![]() .
.
Revenind la
schimbarea de functie ![]() , deducem solutia generala a ecuatiei (3.11)
de forma
, deducem solutia generala a ecuatiei (3.11)
de forma
![]() .
.
Exemple
1. Sa se determine solutia generala a ecuatiei diferentiale
![]() ,
, ![]() .
.
Pasul 1. Punem ecuatia
data sub forma normala, ![]()
![]() . Avem,
. Avem, ![]() ,
, ![]() ,
, ![]() .
.
Pasul 2. Determinam o primitiva a functiei ![]() . Avem
. Avem
![]() ,
, ![]() .
.
Atunci factorul integrant are forma
![]() ,
, ![]() .
.
Pasul 3. Inmultim ecuatia diferentiala sub forma normala cu factorul integrant. Obtinem
![]() .
.
sau echivalent
![]() .
.
Pasul 4. Solutia generala se determina prin cuadraturi: ![]() . In final, obtinem solutia generala sub forma
explicita
. In final, obtinem solutia generala sub forma
explicita
![]() ,
, ![]() ,
, ![]() .
.
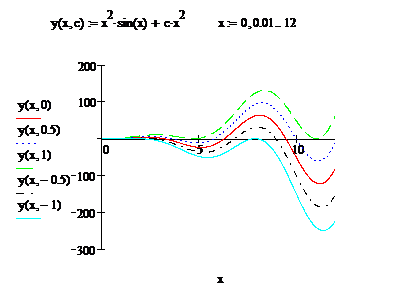
In figura
alaturata sunt reprezentate graficele solutiilor ecuatiei, ![]() , pentru valorile particulare date constantei:
, pentru valorile particulare date constantei: ![]() .
.
2. Sa se determine solutia generala a ecuatiei diferentiale
![]()
![]() .
.
Pasul 1. Ecuatia normala
are forma ![]()
![]() . Avem,
. Avem, ![]() ,
, ![]() ,
, ![]() .
.
Pasul 2. Avem ![]() ,
, ![]() , atunci factorul integrant are forma
, atunci factorul integrant are forma ![]() ,
, ![]() .
.
Pasul 3. Inmultim ecuatia diferentiala sub forma normala cu factorul integrant si obtinem
![]() sau echivalent
sau echivalent ![]() .
.
Pasul 4.
Solutia generala se obtine prin cuadraturi: ![]() . In final, obtinem solutia generala
ecuatiei sub forma explicita
. In final, obtinem solutia generala
ecuatiei sub forma explicita
![]() ,
, ![]() ,
, ![]() .
.
In figura
alaturata sunt reprezentate graficele solutiilor ecuatiei, ![]() , pentru valorile particulare date constantei:
, pentru valorile particulare date constantei: ![]() .
.

Structura solutiei generale a ecuatiei neomogene
Observatie. Fie ecuatia ![]() . Cum
. Cum ![]() este o solutie a
ecuatiei omogene (3.13) si deoarece
este o solutie a
ecuatiei omogene (3.13) si deoarece ![]() este continua si
are derivata
este continua si
are derivata ![]() continua, deci
marginita intr-o vecinatate inchisa a punctului
continua, deci
marginita intr-o vecinatate inchisa a punctului ![]() atunci, potrivit
teoremei lui Picard, probema Cauchy asociata are solutie unica
pentru orice
atunci, potrivit
teoremei lui Picard, probema Cauchy asociata are solutie unica
pentru orice ![]() . Din unicitate rezulta ca nici o alta
solutie, in afara de
. Din unicitate rezulta ca nici o alta
solutie, in afara de ![]() , nu se poate anula pe I.
, nu se poate anula pe I.
Daca ![]() , atunci se separa variabilele si avem
, atunci se separa variabilele si avem
![]() .
.
Integrand ultima ecuatie obtinem
![]() ,
,
unde ![]() este primitiva functiei
este primitiva functiei
![]() pe I. Din aceasta relatie
obtinem
pe I. Din aceasta relatie
obtinem
![]() si deci
si deci ![]()
Deoarece ![]() este functie continua
si pastreaza semnul constant, putem scrie
este functie continua
si pastreaza semnul constant, putem scrie ![]() si atunci
solutia era forma
si atunci
solutia era forma
![]() ,
, ![]() .
.
Datorita
liniaritatii ecuatiei omogene ![]() , putem afirma ca multimea solutiilor maximale ale acestei ecuatii,
, putem afirma ca multimea solutiilor maximale ale acestei ecuatii,
![]()
formeaza un spatiu
vectorial unidimensional cu baza ![]() , unde
, unde ![]() este primitiva functiei
este primitiva functiei ![]() .
.
Observatie. Daca se cunosc doua solutii ![]() si
si ![]() ale ecuatiei
lineare neomogene, atunci functia
ale ecuatiei
lineare neomogene, atunci functia ![]() este o solutie a
ecuatiei omogene asociate. Asadar, daca
este o solutie a
ecuatiei omogene asociate. Asadar, daca ![]() este solutia generala a
ecuatiei lineare omogene asociate si
este solutia generala a
ecuatiei lineare omogene asociate si ![]() este o solutie particulara a
ecuatiei lineare neomogene, atunci orice solutie a ecuatiei
lineare neomogene se obtine cu relatia
este o solutie particulara a
ecuatiei lineare neomogene, atunci orice solutie a ecuatiei
lineare neomogene se obtine cu relatia
![]() (
(
Observatie. Daca se cunosc doua solutii pentru ecuatia lineara neomogena, atunci diferenta lor este solutie a ecuatiei omogene; orice solutie a ecuatiei omogene se obtine prin inmultirea cu o constanta a acestei diferente si deci, se pot gasi fara cuadraturi toate solutiile ecuatiei neomogene. Aceste solutii au forma
![]() .
.
Relatia (* ) arata ca orice solutie a ecuatiei neomogene se poate obtine daca se cunoaste solutia generala a ecuatiei omogene asociate si o solutie particulara a ecuatiei neomogene. Asa cum s-a aratat mai inainte, solutia generala a ecuatiei omogene se obtine prin cuadraturi, aceasta fiind un caz particular de ecuatie cu variabile separabile. Daca nu putem observa o solutie particulara a ecuatiei neomogene atunci, cu metoda variatiei constantelor, folosind formulele (3.25) si (3.26), putem construi o solutie particulara a ecuatiei lineare neomogene. Asadar, solutia generala a ecuatiei neomogene este complet determinata.
Exemplu. Fie ecuatia diferentiala ![]() , care admite solutiile particulare
, care admite solutiile particulare ![]() si
si ![]() . Atunci:
. Atunci:
(a).
Solutia generala are forma ![]() .
.
(b).
Functiile ![]() si
si ![]() se determina scriind
ca
se determina scriind
ca ![]() si
si ![]() verifica
ecuatia data:
verifica
ecuatia data:
![]() atunci,
atunci, ![]() ,
, ![]() .
.
Observatie. Daca membrul drept al ecuatiei neomogene poate fi scris cu ajutorul unor sume finite de functii continue de forma
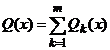
atunci, pentru fiecare functie ![]() ,
, ![]() se determina cate
o solutie particulara, notata cu
se determina cate
o solutie particulara, notata cu ![]() si, folosind
principiul superpozitiei efectelor (ecuatia diferentiala este
lineara), atunci o solutie particulara a ecuatiei neomogene
are forma
si, folosind
principiul superpozitiei efectelor (ecuatia diferentiala este
lineara), atunci o solutie particulara a ecuatiei neomogene
are forma
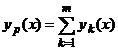 .
.
Intr-adevar, scriind
ca ![]() este o solutie
particulara a ecuatiei neomogene, avem
este o solutie
particulara a ecuatiei neomogene, avem
![]() .
.
Daca scadem aceasta
ecuatie din ecuatia diferentiala normala ![]() , obtinem
, obtinem
![]() .
.
Ultima ecuatie arata
ca functia ![]() este o solutie a
ecuatiei omogene asociate si reciproc, daca
este o solutie a
ecuatiei omogene asociate si reciproc, daca ![]() este solutia
generala a ecuatiei omogene asociate, atunci
este solutia
generala a ecuatiei omogene asociate, atunci
![]()
este solutia generala a ecuatiei neomogene.
Prin urmare, datorita structurii solutiei particulare putem considera ecuatiile neomogene
![]()
![]() ,
,
care au, respectiv
solutiile particulare ![]() si atunci suma
acestor solutii particulare este o solutie particulara a
ecuatiei initiale.
si atunci suma
acestor solutii particulare este o solutie particulara a
ecuatiei initiale.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |