Transformari liniare simetrice
DEFINITIA 1. O transformare liniara F a unui spatiu euclidian in el insusi se numeste simetrica daca satisface conditia
(
,F (
))=(F (),),
I E.
In cele ce urmeaza vom considera dim E = 
.
TEOREMA 1. Conditia necesara si suficienta ca transformarea liniara F I L (E, E) sa fie simetrica este ca:
i) matricea asociata ei intr-o baza ortonormata data sa fie simetrica ;
ii)
produsul scalar (,F ()) sa fie real,
I
E.
Demonstratie. i) Fie B = (e1, e2, ,en) o baza ortonormata, adica
Consideram doi vectori si
I E care, in baza B, se exprima sub forma
si respectiv 
.
Reamintim expresia produsului scalar
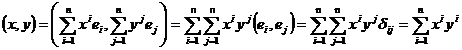
adica
(B[]B, B[]B) = []tB[]B .
Scriind relatia (5) sub forma matriceala avem
(B[]B, B M(F ; B) []B) = (B M(F ; B) []B, B[]B)
si, folosind (6), obtinem urmatoarele forme echivalente
[]tB
M (F ; B)
[]B = (M(F ; B) []B)t[]B
[]tB
M (F ; B)
[]B = []tB
Mt (F ; B)
[]B
M (F ; B) = Mt (F ; B).
ii) Daca F este simetric, atunci (,F ()) = (F (),) = 
, unde bara orizontala de deasupra perechii de paranteze
inseamna conjugatul complex. Deci (,F ()) = si (,F ()) este real, I E.
Reciproc,
daca (,F ()) este real, atunci (,F ()) = = 
= = (F (),) si, prin urmare, F este simetric. □
TEOREMA 1.5.5. Fie E un R - spatiu vectorial, F IL (E, E) si B baza a lui E. Daca M(F ; B) I M(n, R) si M(F ; B) = Mt (F ; B), atunci toate valorile proprii, distincte sau nu, ale endomorfismului F sunt reale.
Demonstratie. Fie M(F ; B) matricea transformarii F fata de o baza ortonormata din E si ecuatia caracteristica asociata ei
det(M (F ; B) - lIn) = 0.
Cum aceasta
ecuatie
este de gradul n in
l,
ea are n radacini
distincte sau nu in
corpul numerelor complexe C. Fie l
una din ele si
[]B o solutie nenula
a ecuatiei vectorilor
proprii (4) din §1.4.3. Consideram
relatia
(4) din § 1.4.3 sub forma
]B = l []B, care, conjugata complex, da
unde 
=M(F ; B), deoarece M(F ; B) IM(n;
R). Amplificand la stanga pe (7) cu 
si pe (8) cu []tB , avem
M (F ; B) []B = l []B
[]Bt M (F ; B)
= 
[]Bt 
Aplicam transpusa relatiei (8 ) si obtinem
M (F ; B) []B = []B ,
care, comparata cu (7 ), da
si, cum 0E , rezulta 
, deci 
I
R.
TEOREMA 1.5.6. Subspatiul ortogonal unui vector propriu al unei transformari liniare simetrice F , este invariant fata de F
Demonstratie.
Fie 
un vector propriu al
lui F corespunzator
valori proprii reale l , a carei
existenta
este asigurata
de teorema precedenta si notam
cu E0 subspatiul lui E ortogonal pe . Atunci pentru I E0 avem
(,F ()) = (F (),) = (l , ) = l (
) = 0 ,
adica
si
F () I E0 si, prin urmare, E0 este invariant fata
de F .
TEOREMA 1.5.7. Pentru orice transformare liniara simetrica F exista o baza ortonormata in E fata de care matricea ei sa aiba forma diagonala.
Demonstratie.
Fie 
un vector propriu
unitar pentru F si 
subspatiul
cu 
dimensiuni ortogonal
pe , fiind invariant fata
de F , restrictia
F , a lui F la , este o transformare liniara de asemenea
simetrica
pe. Considerand un vector propriu unitar 
pentru F , el este propriu si
pentru F si ortogonal pe . Fie apoi 
subspatiul
cu 
dimensiuni ortogonal
pe si
. este de asemenea
invariant fata
de F si fie 
un vector propriu
unitar al restrictiei
F a lui F la . Vectorul este propriu si
pentru F si ortogonal pe si
. Continuand acest proces, dupa pasi obtinem in
o baza
ortonormata
, formata din vectori propii pentru F . Conform T.1.4.4, matricea
transformarii
M(F ; B) are forma diagonala
.
Din aceasta teorema rezulta
Consecinta Subspatiile proprii ale unei transformari liniare simetrice au dimensiunile egale cu ordinele de multiplicitate ale valorilor proprii corespunzatoare si sunt ortogonale doua cate doua.
Practic, pentru a reduce matricea unei transformari liniare simetrice F IL (En, En) la forma diagonala printr-o schimbare ortogonala de baza, procedam astfel:
- Consideram o baza
ortonormata
, fata de care matricea
transformarii este M(F ; B) cu M (F ; B) = Mt (F ; B).
- Scriem ecuatia caracteristica
det (M(F ; B) - 
In) = 0
si gasim
radacinile
care, dupa
cum am vazut,
vor fi toate reale. Forma diagonala
a matricei transformarii F va fi
M(F ; B )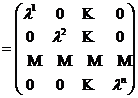
, cu baza B necunoscuta.
- Daca ne intereseaza si baza ortonormata B fata de care matricea M(F ; B ) are forma diagonala de mai sus, cum aceasta trebuie sa fie formata din vectori proprii, procedam in felul urmator. Consideram ecuatia vectorilor proprii
(M (F ; B) - lIn)[]B = [
]B
si inlocuind,
pe rand, cu fiecare radacina
caracteristica
, determinam subspatiile proprii 
. Cu ajutorul procedeului Gram-Schmidt construim, pornind de
la un sistem fundamental de solutii
ale sistemului (M (F B) - In)[]B = []B, cate o baza ortonormata in
fiecare . Cum subspatiile sunt ortogonale cate
doua
si
suma dimensiunilor lor este , rezulta ca aceste baze vor
constitui impreuna
o baza
ortonormata
in
, fata de care matricea
transformarii
F are
forma diagonala
M(F ; B
|
Politica de confidentialitate |
 .com |
Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Sisteme de ecuatii si transformari liniare. (Regula lui Cramer) |
| Transformari liniare simetrice |
| MODELAREA COMPORTARII IN FUNCTIONARE A INSTALATIILOR TEHNOLOGICE CU AJUTORUL LANTURILOR MARKOV |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
