Polinom caracteristic
In cele ce urmeaza ne vom ocupa de determinarea valorilor proprii si a vectorilor proprii pentru F IL (E, E).
Fie I endomorfismul
unitate, I (![]() )
)![]() ,
, ![]() . Egalitatea (1) este echivalenta cu
. Egalitatea (1) este echivalenta cu
(3) (F -![]() I )(
I )(![]() ) = 0E .
) = 0E .
Fie B o baza
in
E, M(F ; B)![]() si
M (I ;
B) = In, unde In este matricea unitate de ordinul n = dim E. La randul ei, egalitatea (3) este echivalenta cu
si
M (I ;
B) = In, unde In este matricea unitate de ordinul n = dim E. La randul ei, egalitatea (3) este echivalenta cu
(M(F ; B) - ![]() In)[
In)[![]() ]B = [0E]B ,
]B = [0E]B ,
unde [![]() ]B este matricea coloana formata din coordonatele lui
]B este matricea coloana formata din coordonatele lui ![]() in baza B.
in baza B.
DEFINITIA 1. Egalitatea data de relatia (4) se numeste ecuatia vectorilor proprii.
Aceasta este folosita pentru determinarea coordonatelor (![]() ) ale vectorului propriu
) ale vectorului propriu ![]() atunci cand se cunoaste valoarea proprie
atunci cand se cunoaste valoarea proprie ![]() .
.
Ecuatia matriceala (4) se scrie explicit sub forma
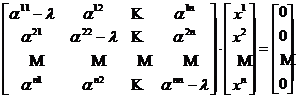 , (unde 0=0K)
, (unde 0=0K)
care este echivalenta cu sistemul
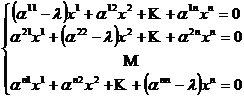
de n ecuatii
liniare si
omogene in
necunoscutele 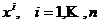 , pentru care solutia banala nu convine deoarece
, pentru care solutia banala nu convine deoarece ![]() I E . Deci
valorile proprii sunt acele valori ale lui
I E . Deci
valorile proprii sunt acele valori ale lui ![]() pentru care determinantul atasat
matricei sistemului este nul.
pentru care determinantul atasat
matricei sistemului este nul.
DEFINITIA1. Polinomul
P(![]() ) = det (M(F ; B) -
) = det (M(F ; B) - ![]() In)
In)
se numeste
polinomul caracteristic al
endomorfismului F , iar P(![]() )=0 se numeste ecuatia
caracteristica
a lui F
)=0 se numeste ecuatia
caracteristica
a lui F
TEOREMA 1. Polinomul caracteristic al unui endomorfism F este un invariant la schimbarea bazei spatiului vectorial E.
Demonstratie.
Fie B si ![]() doua
baze in
E, F IL (E,E) cu M(F ; B), M(F ,
doua
baze in
E, F IL (E,E) cu M(F ; B), M(F , ![]() ) matricele asociate lui F in cele doua baze si
polinoamele caracteristice ale lui F in cele
doua
baze
) matricele asociate lui F in cele doua baze si
polinoamele caracteristice ale lui F in cele
doua
baze
![]() ( M(F ; B)
( M(F ; B)![]() , respectiv,
, respectiv, ![]() ( M(F ,
( M(F , ![]() )
)![]() .
.
Conform egalitatii (14), a teoremei 1.3.10,
M(F , ![]() )
)![]() M(F ; B)
M(F ; B)![]() ,
,
unde M(B, ![]() ) este matricea de trecere de la B la
) este matricea de trecere de la B la ![]() . Avem in mod evident ca
. Avem in mod evident ca
In = M-1(B, ![]() ) In
M(B,
) In
M(B, ![]() )
)
si prin urmare
![]() M(F ; B)
M(F ; B) ![]() -
- ![]()
![]() ( M(F ; B)
( M(F ; B)![]()
![]() ( M(F ; B)
( M(F ; B)![]() ,
,
deoarece determinantul produsului a doua matrice patrate de acelasi ordin este egal cu produsul determinantilor celor doua matrice patrate.
Acest
rezultat justifica
de ce P(![]() ) a fost numit, simplu, polinomul caracteristic al lui F si nu polinomul caracteristic al lui F in baza B.
) a fost numit, simplu, polinomul caracteristic al lui F si nu polinomul caracteristic al lui F in baza B.
TEOREMA 1. Fie E un K - spatiu vectorial si F I L (E, E). Daca K este un corp algebric inchis, endomorfismul F admite valori proprii si vectori proprii.
Demonstratie.
P(![]() ) este un polinom cu grad P(
) este un polinom cu grad P(![]() )
)![]() si cu coeficientii din
corpul K. Daca K este algebric inchis, ecuatia
P
si cu coeficientii din
corpul K. Daca K este algebric inchis, ecuatia
P![]() admite cel putin o solutie
admite cel putin o solutie
![]() K . Printr-un
procedeu cunoscut, din aproape in aproape se obtine
descompunerea
K . Printr-un
procedeu cunoscut, din aproape in aproape se obtine
descompunerea
![]()
cu ![]() . Valorile proprii ale endomorfismului F sunt
. Valorile proprii ale endomorfismului F sunt![]() , cu ordinele de multiplicitate
, cu ordinele de multiplicitate
![]() .
.
Unei
valori proprii ![]() ii
corespunde o infinitate de vectori proprii care au coordonatele in baza B
date de sistemul (5), in care
ii
corespunde o infinitate de vectori proprii care au coordonatele in baza B
date de sistemul (5), in care ![]() este inlocuit cu
este inlocuit cu ![]() .
.
In particular, daca K = C, orice endomorfism F I L (E, E) admite valori proprii si vectori proprii. Daca K = R, nu orice F I L (E, E) admite valori proprii si vectori proprii.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |