Forma diagonala
O preocupare importanta in cele ce urmeaza este determinarea unei baze in E,
astfel incat matricea unui endomorfism F I L (E,E) sa aiba forma cea mai simpla, asa numita forma canonica . Pentru acest motiv, determinarea unei baze in care matricea endomorfismului F are forma diagonala, prezinta un interes deosebit. Dat fiind un endomorfism prin matricea sa intr-o baza arbitrara, aceasta operatie se numeste reducerea matricei respective la forma diagonala sau diagonalizarea matricei.
DEFINITIA1.4.6. Vom spune ca endomorfismul F I L (E,E) este diagonalizabil daca exista o baza B in E in care
M(F ;B)![]()
este o matrice diagonala, adica ![]() K pentru i j.
K pentru i j.
TEOREMA 1.4.6. Un endomorfism F I L (En, En) este diagonalizabil daca si numai daca exista o baza a spatiului Vn formata din vectori proprii ai endomorfismului.
Demonstratie. Daca
F este diagonalizabil, atunci
exista o baza![]() a spatiului fata de care matricea este
diagonala
a spatiului fata de care matricea este
diagonala
M(F ; B)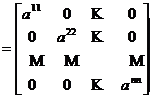 .
.
Rezulta
F ![]() ( F ;
( F ;![]() )
)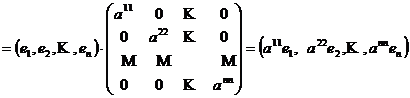
si cum F (B)=( F (![]() ),F (
),F (![]() ),.,F (
),.,F (![]() )), obtinem F
)), obtinem F ![]() , ceea ce inseamna ca vectorii
, ceea ce inseamna ca vectorii ![]() sunt vectori proprii ai endomorfismului
F
sunt vectori proprii ai endomorfismului
F
Reciproc,
daca ![]() este o baza in En
formata de vectorii proprii ai lui F , adica F
este o baza in En
formata de vectorii proprii ai lui F , adica F ![]() , atunci matricea lui F in aceasta baza este
, atunci matricea lui F in aceasta baza este
M(F ; B*)=![]() F
F ![]()
![]()
![]() F
F ![]()
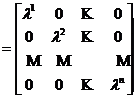 .
.
Desigur,
unele dintre numerele ![]() pot fi egale.
pot fi egale.
TEOREMA1.4.7. Pentru endomorfismul F I L (En, En), dimensiunea unui subspatiu propriu este cel mult egala cu ordinul de multiplicitate al valorii proprii corespunzatoare subspatiului.
Demonstratie.
Fie ![]() o valoare proprie
multipla de ordinul m si E0
subspatiul propriu corespunzator, cu
o valoare proprie
multipla de ordinul m si E0
subspatiul propriu corespunzator, cu ![]() . Fie
. Fie ![]() o baza a
subspatiului propriu. Completam aceasta baza pana la o
baza in En de forma
o baza a
subspatiului propriu. Completam aceasta baza pana la o
baza in En de forma ![]() . Deoarece vectorii
. Deoarece vectorii ![]() , sunt vectori proprii corespunzatori valorii proprii
, sunt vectori proprii corespunzatori valorii proprii ![]() , avem F
, avem F ![]() si
si
F ![]() . Matricea lui F in aceasta
baza este
. Matricea lui F in aceasta
baza este
M(F ,, B)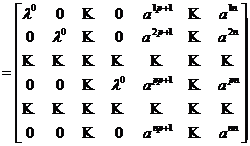
astfel ca polinomul caracteristic al lui F are forma
![]() ( M(F ; B)
( M(F ; B)![]()
![]() ,
,
unde ![]() este un determinant de
ordin
este un determinant de
ordin ![]() .
.
In concluzie, ![]() implica
implica![]() , iar
, iar![]() implica
implica ![]() . Deci
. Deci![]() .
.
TEOREMA 1.4.8. Un endomorfism F I L (En, En) este diagonalizabil daca si numai daca polinomul caracteristic are toate radacinile in campul peste care este luat En si dimensiunea fiecarui subspatiu propriu este egala ca ordinul de multiplicitate al
valorii proprii corespunzatoare.
Demonstratie.
Presupunem ca endomorfismul F este diagonalizabil. Rezulta ca
exista o baza ![]() formata din vectori proprii pentru F , fata de care
matricea lui F este diagonala. Fie
formata din vectori proprii pentru F , fata de care
matricea lui F este diagonala. Fie
![]() ,
,
adica ![]() sunt valorile proprii
ale lui F de multiplicitati
sunt valorile proprii
ale lui F de multiplicitati ![]() cu
cu ![]() . Fara a reduce generalitatea, putem admite ca
primii
. Fara a reduce generalitatea, putem admite ca
primii ![]() vectori din baza
vectori din baza ![]() corespund lui
corespund lui ![]() , urmatorii
, urmatorii ![]() lui
lui ![]() , etc. In concluzie, vectorii
, etc. In concluzie, vectorii ![]() apartin
subspatiului propriu corespunzator valorii proprii
apartin
subspatiului propriu corespunzator valorii proprii ![]() , ceea ce inseamna ca numarul lor
, ceea ce inseamna ca numarul lor ![]() este mai mic sau cel
mult egal cu
este mai mic sau cel
mult egal cu ![]() , adica
, adica ![]() . Pe de alta parte, conform teoremei 1.4.7, avem
. Pe de alta parte, conform teoremei 1.4.7, avem ![]() . In concluzie
. In concluzie ![]() . Analog, rezulta
. Analog, rezulta
![]() .
.
Reciproc, presupunem
ca ![]() . Consideram
multimea
. Consideram
multimea ![]() , cu
, cu ![]() , formata din vectori din En astfel incat primii
, formata din vectori din En astfel incat primii ![]() vectori sa
constituie o baza in E1,
urmatorii
vectori sa
constituie o baza in E1,
urmatorii ![]() sa constituie o
baza in E2 si
asa mai departe. Folosind inductia asupra lui p se arata ca
B este o baza a lui En.
Fata de aceasta baza B matricea lui F este
sa constituie o
baza in E2 si
asa mai departe. Folosind inductia asupra lui p se arata ca
B este o baza a lui En.
Fata de aceasta baza B matricea lui F este
M(F ; B)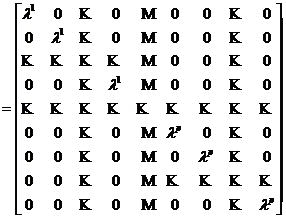 ,
,
adica o matrice diagonala.
Consecinta
1.4.1. Daca
F I L (En, En)
este diagonalizabil, atunci En
este suma directa a subspatiilor proprii asociate valorilor
proprii ![]() ale endomorfismului,
adica
ale endomorfismului,
adica ![]() .
.
Procedeu de diagonalizare a unui endomorfism. Practic se parcurg urmatoarele etape :
Fixam o baza B in En si determinam matricea M(F ; B).
Determinam valorile
proprii care sunt solutii in K ale ecuatiei ![]() .
.
Daca exista ![]() valori proprii
distincte
valori proprii
distincte ![]() cu ordinele de
multiplicitate
cu ordinele de
multiplicitate 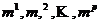 , calculam rangul fiecarei matrice M(F ; B)
, calculam rangul fiecarei matrice M(F ; B)![]() . Daca
. Daca
rang(M(F ; B) ![]() ,
, ![]() ( F
( F ![]() I )) este numarul
solutiilor independente ale sistemului omogen (M(F ; B)
I )) este numarul
solutiilor independente ale sistemului omogen (M(F ; B)![]() , atunci (conform teoremei 1.4.8) endomorfismul F este diagonalizabil.
, atunci (conform teoremei 1.4.8) endomorfismul F este diagonalizabil.
Se
rezolva cele ![]() sisteme omogene (M(F ; B)
sisteme omogene (M(F ; B)![]() ,
, ![]() . Un sistem fundamental de solutii, pentru un asemenea
sistem, reprezinta coordonatele vectorilor proprii corespunzatori
valorii proprii
. Un sistem fundamental de solutii, pentru un asemenea
sistem, reprezinta coordonatele vectorilor proprii corespunzatori
valorii proprii ![]() .
.
Matricea lui F ,
in raport cu baza formata din vectorii proprii ai lui F , are pe diagonala elementele ![]() , adica valorile proprii.
, adica valorile proprii.
Notam prin DIM (n, n, K) matricea diagonala atasata lui F in raport cu baza formata din vectorii proprii ai lui F . Daca CIM (n, n, K) este matricea ale carei coloane sunt vectorii proprii care alcatuiesc noua baza a lui En, adica matricea de trecerea de la baza initiala din En (baza canonica B) la baza formata din vectorii proprii, atunci
D = C-1 M(F ; B) C
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |