
Vectori proprii. Valori proprii. Definitii. Proprietati
Fie E un K -spatiu vectorial.
DEFINITIA 1. Un
vector ![]() I E se numeste
vector propriu al endomorfismului F I L (E,E) daca l I
K astfel incat
I E se numeste
vector propriu al endomorfismului F I L (E,E) daca l I
K astfel incat
F (![]() ) = l
) = l![]() .
.
Un
scalar l I
K se numeste valoare proprie a endomorfismului F I L (E,E) daca ![]() I
E care verifica egalitatea (1).
I
E care verifica egalitatea (1).
Observatii 1. (a) Unui vector propriu ii corespunde o singura valoare proprie.
Intr-adevar,
F (![]() )=
)=![]()
![]() si F (
si F (![]() )
)![]() , deoarece
, deoarece ![]() .
.
(b) Unei valori proprii ![]() ii
corespund o infinitate de vectori proprii.
ii
corespund o infinitate de vectori proprii.
Intr-adevar,
daca
![]() este vector propriu
asociat valorii proprii
este vector propriu
asociat valorii proprii ![]() ( adica F (
( adica F (![]() )
)![]() ), atunci toti
vectorii subspatiului
), atunci toti
vectorii subspatiului
![]() generat de
generat de ![]() , mai putin vectorul nul 0E, vor fi vectori
proprii asociati valorii
proprii
, mai putin vectorul nul 0E, vor fi vectori
proprii asociati valorii
proprii ![]() (deoarece F (
(deoarece F (![]() )
)![]() ,
,
![]() I K ).
I K ).
TEOREMA 1.
Vectorii proprii ![]() ai unui endomorfism F , asociati
unor valori proprii distincte
ai unui endomorfism F , asociati
unor valori proprii distincte ![]() , sunt liniar independenti.
, sunt liniar independenti.
Demonstratie. Presupunem contrariul : ![]() I K nu toti nuli, astfel
incat
I K nu toti nuli, astfel
incat
![]() .
.
Dispunem de numerotare si putem face ca ![]() 0K. Din aceasta deducem
0K. Din aceasta deducem
![]() F (
F (![]() ) +
) + ![]() F (
F (![]() ) + +
) + + ![]() F (
F (![]() ) = 0E
) = 0E
sau, tinand seama ca ![]() sunt vectori proprii,
sunt vectori proprii,
![]() .
.
Inmultim (2) cu ![]() si o scadem din (2'),
si o scadem din (2'),
![]() .
.
Daca indE, din aceasta ultima egalitate, cu![]() distincte, rezulta
distincte, rezulta
![]() si
(2) se reduce la
si
(2) se reduce la![]() , cu
, cu![]() 0K, deci
0K, deci ![]() . Dar
. Dar ![]() este vector propriu si
conform cu D.1.4.2,
este vector propriu si
conform cu D.1.4.2, ![]() 0E. Prin urmare nu
are loc indE. Am demonstrat
astfel ca
0E. Prin urmare nu
are loc indE. Am demonstrat
astfel ca
depE T depE.
Repetand rationamentul, obtinem
depE T depE T T depE ,
ceea ce este fals
deoarece ![]() 0E si
0E si ![]() (care da
indE).
(care da
indE).
In concluzie, indE .
DEFINITIA 1. Fie ![]() o valoare proprie a
endomorfismului F I L
(E,E). Multimea Ej = se numeste subspatiul propriu asociat valorii proprii
o valoare proprie a
endomorfismului F I L
(E,E). Multimea Ej = se numeste subspatiul propriu asociat valorii proprii ![]() .
.
Se
observa
ca
![]() este format din
vectorul nul si
toti
vectorii proprii asociati valorii proprii
este format din
vectorul nul si
toti
vectorii proprii asociati valorii proprii![]() .
.
TEOREMA 1.4.3. (a subspatiilor proprii).
(P.1.)
Subspatiul
propriu Ej , asociat valorii proprii![]() , este un subspatiu vectorial al lui E, invariant fata de F
, este un subspatiu vectorial al lui E, invariant fata de F
(P.2.)
Subspatiile
proprii asociate valorilor proprii distincte ![]() , au proprietatea ca E1
E2 = .
, au proprietatea ca E1
E2 = .
Demonstratie.
(P.1.) Sa
aratam
mai intai
ca
![]() / K
E / K. Egalitatea F (
/ K
E / K. Egalitatea F (![]() ) =
) =![]() se mai scrie (F -
se mai scrie (F -![]() I )(
I )(![]() ) = 0E, cu I transformarea identica.
Deci
) = 0E, cu I transformarea identica.
Deci ![]() este nucleul
endomorfismului F -
este nucleul
endomorfismului F -![]() I si, conform cu T1.3.4, este un subspatiu
vectorial al lui E.
I si, conform cu T1.3.4, este un subspatiu
vectorial al lui E.
Subspatiul ![]() este invariant fata
de F deoarece
este invariant fata
de F deoarece
![]() , F (
, F (![]() )
)![]() (conform D.1.4.1) .
(conform D.1.4.1) .
(P.2.) Fie
![]() . Pentru
. Pentru 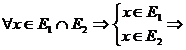 F
F ![]() , F
, F ![]() T
T
![]() si
si ![]() T
T ![]() = 0E T E1
E2 = .
= 0E T E1
E2 = .
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |