
Tipuri simple de ecuatii diferentiale integrabile prin cuadraturi
Vom studia o clasa importanta de ecuatii diferentiale de ordinal intai, a caror rezolvare se reduce la calculul unor primitive (calculul integralelor nedefinite (!)), sau pastrand traditia istorica, vom spune ca integrarea acestor ecuatii diferentiale se face prin cuadraturi[1]
Ecuatii cu variabile separabile (e.d.v.s.).
Cele
mai simple ecuatii diferentiale de ordinul intai sunt ecuatiile
cu variabile separabile . Aceste ecuatii sunt definite de
functiile ![]() si
si ![]() , unde
, unde ![]() sunt intervale, iar
sunt intervale, iar ![]() si
si ![]() sunt functii
continue pe domeniile lor de definitie (
sunt functii
continue pe domeniile lor de definitie (![]() si
si ![]() ) si au forma generala
) si au forma generala
![]() sau echivalent
sau echivalent ![]() . (2.1)
. (2.1)
Vom observa
ca pentru acest tip de ecuatii putem regrupa intr-o parte a
egalitatii numai expresia ![]() , care depinde exclusiv de variabila
, care depinde exclusiv de variabila![]() si de cealalta parte pe
si de cealalta parte pe ![]() , care depinde numai de
, care depinde numai de![]() .
.
Definitie. Functia ![]() ,
, ![]() , este o solutie a
ecuatiei (2.1) daca si
numai daca
, este o solutie a
ecuatiei (2.1) daca si
numai daca ![]() este derivabila
pe
este derivabila
pe ![]() ,
, ![]() si verifica
relatia
si verifica
relatia
![]() ,
, ![]() . (2.2)
. (2.2)
In continuare vom analiza cazurile:
a). Daca ![]() pentru orice
pentru orice ![]() , atunci ecuatia (2.1) are forma
, atunci ecuatia (2.1) are forma ![]() , unde
, unde ![]() este functie continua. In acest caz
multimea solutiilor ecuatiei
este definita de curbele integrale (solutiile
sunt curbe plane, continute in
este functie continua. In acest caz
multimea solutiilor ecuatiei
este definita de curbele integrale (solutiile
sunt curbe plane, continute in ![]() , care se obtin prin integrare; in acest caz solutiile
se obtin cu ajutorul multimii primitivelor functiei
, care se obtin prin integrare; in acest caz solutiile
se obtin cu ajutorul multimii primitivelor functiei ![]() )
)
![]() ,
,
unde ![]() este o primitiva
a functiei
este o primitiva
a functiei ![]() pe
pe ![]() , iar
, iar ![]() este
este
Curbele integrale (2.3) se deduc
unele din altele printr-o translatie in directia axei ![]() , acoperind tot domeniul
, acoperind tot domeniul ![]() . Solutia problemei Cauchy, cu datele initiale
. Solutia problemei Cauchy, cu datele initiale ![]() este unica
si putem scrie
este unica
si putem scrie
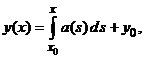 sau
sau ![]() . (2.4)
. (2.4)
b). Daca ![]() pentru orice
pentru orice ![]() , atunci ecuatia (2.1) devine
, atunci ecuatia (2.1) devine
![]() ,
(2.5)
,
(2.5)
unde ![]() este functie continua. Vom observa ca daca
este functie continua. Vom observa ca daca
![]() sunt radacinile
reale ale ecuatiei
sunt radacinile
reale ale ecuatiei ![]() situate in intervalul
situate in intervalul ![]() , atunci functiile constante
, atunci functiile constante
![]()
![]() , (2.6)
, (2.6)
sunt solutii ale ecuatiei diferentiale (2.5), numite solutii stationare.
Fie multimea deschisa ![]() . Pe multimea
. Pe multimea ![]() se separa
variabilele inlocuind ecuatia diferentiala (1.5) cu ecuatia
se separa
variabilele inlocuind ecuatia diferentiala (1.5) cu ecuatia
![]() , (2.7)
, (2.7)
si se determina cate o primitiva in fiecare membru al egalitatii (2.7):
![]() .
.
Asadar, multimea solutiilor ecuatiei (2.7) este definita de curbele integrale (definite implicit)
![]() , (2.8)
, (2.8)
unde ![]() este o primitiva
a functiei continue
este o primitiva
a functiei continue ![]() , definita pe fiecare din intervalele deschise
, definita pe fiecare din intervalele deschise ![]() , unde
, unde ![]() sunt
radacinile reale ale ecuatiei
sunt
radacinile reale ale ecuatiei ![]() . In fiecare domeniu de tip banda, avand forma
. In fiecare domeniu de tip banda, avand forma ![]() , curbele integrale (2.8) se deduc unele din altele printr-o
translatie in directia axei
, curbele integrale (2.8) se deduc unele din altele printr-o
translatie in directia axei ![]() .
.
Vom observa ca ![]() pentru
pentru ![]() si atunci
primitiva
si atunci
primitiva ![]() , unde
, unde ![]() (capetele intervalului
(capetele intervalului![]() pot fi
pot fi ![]() (!)), este
bijectiva, deci inversabila. Asadar, este posibil ca solutiile
(2.8) sa fie explicitate in raport cu
(!)), este
bijectiva, deci inversabila. Asadar, este posibil ca solutiile
(2.8) sa fie explicitate in raport cu ![]() , si cel putin formal, putem scrie
, si cel putin formal, putem scrie
![]() . (2.9)
. (2.9)
c). Consideram cazul general,
cand ecuatia diferentiala are forma, ![]() . Fie
. Fie ![]() un subinterval
maximal, fixat, din
un subinterval
maximal, fixat, din ![]() , pe care vom presupune ca
, pe care vom presupune ca ![]() pentru orice
pentru orice ![]() si, fie
multimea deschisa
si, fie
multimea deschisa
![]() .
.
Daca ![]() este o solutie a
ecuatiei (2.1) atunci, potrivit definitiei, pe
este o solutie a
ecuatiei (2.1) atunci, potrivit definitiei, pe ![]() se verifica ecuatia
se verifica ecuatia
![]() . (2.10)
. (2.10)
Fie ![]() o primitiva a
functiei
o primitiva a
functiei ![]() , deci
, deci ![]() este
derivabila si
este
derivabila si ![]() pentru orice
pentru orice ![]() . Functia compusa
. Functia compusa ![]() este evident
derivabila pe
este evident
derivabila pe ![]() si avem
si avem
![]() oricare ar fi
oricare ar fi ![]() .
.
Asadar, putem scrie ![]() si daca
si daca ![]() este o primitiva
a functiei
este o primitiva
a functiei ![]() pe
pe ![]() atunci
atunci
![]() , (2.11)
, (2.11)
unde ![]() este o
este o
Deoarece 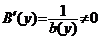 , atunci functia
, atunci functia ![]() pastreaza
semn constant pe
pastreaza
semn constant pe ![]() si prin urmare
functia continua
si prin urmare
functia continua ![]() este strict
monotona, deci inversabila pe
este strict
monotona, deci inversabila pe ![]() . Din (2.11) deducem
. Din (2.11) deducem
![]() , (2.12)
, (2.12)
care reprezinta solutia generala sub forma explicita.
Relatia (2.12) arata modul
cum se obtin solutiile ecuatiei cu variabile separabile (2.1).
Altfel spus, daca ![]() este o solutie a
ecuatiei (2.1), atunci ea este individualizata pana la o
constanta arbitrara de relatia
este o solutie a
ecuatiei (2.1), atunci ea este individualizata pana la o
constanta arbitrara de relatia ![]() , unde
, unde ![]() este o primitiva
a functiei
este o primitiva
a functiei ![]() ,
, ![]() este o primitiva
a functiei
este o primitiva
a functiei ![]() pe
pe ![]() , iar
, iar ![]() este constanta
reala .
este constanta
reala .
Reciproc, vom arata ca orice
functie ![]() apartinand
familiei (2.12) este solutie a ecuatiei diferentiale (2.1) pe multimea
deschisa
apartinand
familiei (2.12) este solutie a ecuatiei diferentiale (2.1) pe multimea
deschisa ![]() . Intr-adevar, din egalitatea (2.12), avem
. Intr-adevar, din egalitatea (2.12), avem ![]() . Prin derivare, obtinem
. Prin derivare, obtinem ![]() , sau
, sau ![]() , si deci
, si deci ![]() . Ultima relatie arata ca functia
. Ultima relatie arata ca functia ![]() este solutie a
ecuatiei (2.1). Intervalul maxim de definitie al acestei solutii
este format din toate punctele
este solutie a
ecuatiei (2.1). Intervalul maxim de definitie al acestei solutii
este format din toate punctele ![]() astfel incat
astfel incat ![]() , unde
, unde ![]() este intervalul maxim de
definitie al functiei
este intervalul maxim de
definitie al functiei ![]() .
.
Asadar,
solutia (2.12) impreuna cu solutiile
stationare ![]() si eventual cu
unele prelungiri posibile! ale solutiei generale formeaza
multimea solutiilor ecuatiei (2.1) (vezi Propozitia 1
si exemplele 2 si 3).
si eventual cu
unele prelungiri posibile! ale solutiei generale formeaza
multimea solutiilor ecuatiei (2.1) (vezi Propozitia 1
si exemplele 2 si 3).
Propozitia 1. Fie
![]() ,
, ![]() o functie continua care defineste ecuatia
diferentiala sub forma normala
o functie continua care defineste ecuatia
diferentiala sub forma normala
![]() , (2.13)
, (2.13)
si ![]() doua solutii ale ecuatiei diferentiale(2.13) astfel incat
doua solutii ale ecuatiei diferentiale(2.13) astfel incat
![]() . (2.14)
. (2.14)
Atunci functia ![]() definita prin
definita prin
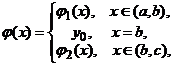 (2.15)
(2.15)
este solutie a ecuatiei
Daca
se da un punct initial ![]() , si se cer solutiile ecuatiei (2.1), care
verifica conditia initiala
, si se cer solutiile ecuatiei (2.1), care
verifica conditia initiala ![]() , atunci pentru integrarea (e.d.v.s) procedam
astfel:
, atunci pentru integrarea (e.d.v.s) procedam
astfel:
i). se constata daca ![]() este solutie
stationara (
este solutie
stationara (![]() ) si in caz afirmativ, se retine solutia
stationara
) si in caz afirmativ, se retine solutia
stationara ![]() .
.
In cazul in care ![]() este o primitiva
a functiei
este o primitiva
a functiei ![]() pe
pe ![]() , se cerceteaza daca aceasta se poate prelungi
si in punctul
, se cerceteaza daca aceasta se poate prelungi
si in punctul ![]() cand
cand ![]() . In caz afirmativ, se determina
. In caz afirmativ, se determina ![]() astfel incat in (2.11),
sa avem
astfel incat in (2.11),
sa avem ![]() si se retine
solutia particulara
si se retine
solutia particulara ![]() determinata
implicit de relatia
determinata
implicit de relatia
![]() . (2.16)
. (2.16)
ii) Atunci cand se da punctul initial
![]() , primitivele
, primitivele ![]() si
si ![]() pot fi inlocuite cu
expresiile
pot fi inlocuite cu
expresiile
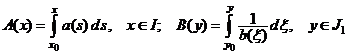 , (2.17)
, (2.17)
si
functia ![]() definita implicit
de ecuatia
definita implicit
de ecuatia ![]() defineste o
solutie locala a problemei Cauchy (2.1) si conditia
initiala
defineste o
solutie locala a problemei Cauchy (2.1) si conditia
initiala ![]() .
.
Folosind structura solutiilor ecuatiei (2.1) putem enunta urmatoarea
Propozitia
2. (Existenta si unicitatea
solutiilor ecuatiei cu variabile separabile). Daca
functiile continue ![]()
![]() , definesc
ecuatia cu variabile separabile (2.1), atunci
, definesc
ecuatia cu variabile separabile (2.1), atunci
i).Pentru orice ![]() , exista o vecinatate
, exista o vecinatate
![]() si exista o
solutie
si exista o
solutie ![]() a ecuatiei (2.1) astfel incat
a ecuatiei (2.1) astfel incat ![]() .
.
Exemple
Sa se determine solutiile ecuatiei
diferentiale ![]() .
.
Introducem functiile ![]() , iar
, iar ![]() . Domeniul maximal de definitie al ecuatiei este format
din reuniunea multimilor deschise
. Domeniul maximal de definitie al ecuatiei este format
din reuniunea multimilor deschise
![]() .
.
Se constata ca ![]() . Pentru separarea variabilelor vom considera domeniul
. Pentru separarea variabilelor vom considera domeniul
![]() .
.
Ecuatia poate fi scrisa
cu ajutorul diferentialelor sub forma ![]() , apoi prin integrarea fiecarui membru obtinem
, apoi prin integrarea fiecarui membru obtinem ![]() . Fie
. Fie ![]() o primitiva a
functiei
o primitiva a
functiei ![]() si
si ![]() o primitiva a
functiei
o primitiva a
functiei ![]() . Atunci din
. Atunci din ![]() obtinem solutia generala sub forma
implicita
obtinem solutia generala sub forma
implicita
![]() . (*)
. (*)
 Relatia (*) se poate explicita in raport cu
Relatia (*) se poate explicita in raport cu ![]() si atunci solutia generala sub forma
explicita este data de familia
si atunci solutia generala sub forma
explicita este data de familia
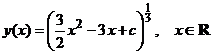 ,
,
unde![]() . Graficele acestor functii reprezinta
solutiile integrale ale ecuatiei considerate.
. Graficele acestor functii reprezinta
solutiile integrale ale ecuatiei considerate.
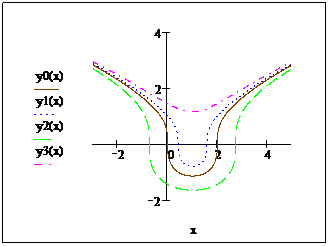
In figura alaturata
sunt reprezentate graficele solutiilor ![]() ,
, ![]() ,
, ![]() ,
, ![]() pentru valorile particulare
pentru valorile particulare ![]() ,
, ![]() respectiv,
respectiv, ![]() date constantelor.
date constantelor.
Determinati solutiile ecuatiei ![]() .
.
Introducem notatiile ![]() . Asadar, domeniul maxim de definitie este
. Asadar, domeniul maxim de definitie este ![]() .
.
Ecuatia ![]() are
radacinile
are
radacinile ![]() si
si ![]() si atunci
exista doua solutii
stationare
si atunci
exista doua solutii
stationare ![]() si
si ![]() ,
, ![]() .
.
Fie domeniul maximal ![]() . Evident, avem
. Evident, avem
![]() .
.
Separand variabilele
ecuatiei date, pe fiecare din subdomeniile deschise ale reuniunii ![]() , putem scrie ecuatia
, putem scrie ecuatia
![]() . (1)
. (1)
Integrand ambii membri ai acestei ecuatii obtinem solutia generala sub forma implicita
![]() sau
sau ![]() ,
, ![]() . (2)
. (2)
Observam ca relatia
(2) poate fi explicitata in raport cu ![]() si pentru orice
si pentru orice ![]() , fixat, corespunzator domeniului
, fixat, corespunzator domeniului ![]() , obtinem trei familii de solutii sub forma explicita:
, obtinem trei familii de solutii sub forma explicita:
generala a ecuatiei se expliciteaza sub forma
![]() ;
;
expliciteaza sub forma
![]() ;
;
generala a ecuatiei se expliciteaza sub forma
![]() ;
;
 Solutiile
Solutiile ![]() si
si ![]() sunt solutii maximale, dar nu sunt solutii globale, in sensul ca
ele nu mai pot fi prelungite pe
sunt solutii maximale, dar nu sunt solutii globale, in sensul ca
ele nu mai pot fi prelungite pe ![]() in afara intervalalor
maxime de definitie
in afara intervalalor
maxime de definitie ![]() respectiv,
respectiv, ![]() . Solutia
. Solutia ![]() este o solutie globala.
este o solutie globala.
Asadar, ecuatia
data are solutiile generale
![]() ,
, ![]() si
si ![]() , definite pe intervalele maximale respective si, solutiile stationare
, definite pe intervalele maximale respective si, solutiile stationare
![]() si
si ![]() ,
, ![]() .
.
Solutia stationara ![]() este asimptota orizontala
curbelor integrale
este asimptota orizontala
curbelor integrale ![]() si
si ![]() , cand
, cand ![]() . Daca admitem pentru
. Daca admitem pentru ![]() valoarea
valoarea ![]() , atunci din oricare dintre solutiile generale mentionate
se obtine solutia
, atunci din oricare dintre solutiile generale mentionate
se obtine solutia ![]() . In acest caz putem spune ca de fapt solutia
. In acest caz putem spune ca de fapt solutia ![]() ,
, ![]() , este o solutie
particulara a ecuatiei considerate.
, este o solutie
particulara a ecuatiei considerate.
Solutia stationara
![]() , este asimptota orizontala atat curbei integrale
, este asimptota orizontala atat curbei integrale ![]() cat si curbei
integrale
cat si curbei
integrale ![]() , cand
, cand ![]() . Daca admitem valoarea
. Daca admitem valoarea ![]() , atunci din oricare dintre solutiile generale
mentionate se obtine solutia
, atunci din oricare dintre solutiile generale
mentionate se obtine solutia ![]() . Evident, in acest caz spunem ca solutia
. Evident, in acest caz spunem ca solutia ![]() ,
, ![]() , este o solutie
particulara a ecuatiei considerate.
, este o solutie
particulara a ecuatiei considerate.
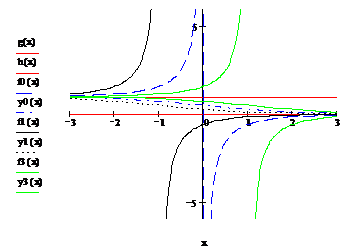
In figura alaturata
sunt reprezentate solutiile stationare notate cu ![]() si
si ![]() si solutiile
maximale, pentru valorile
si solutiile
maximale, pentru valorile ![]() ,
, ![]() si
si ![]() , notate respectiv, cu
, notate respectiv, cu ![]()
![]() si
si ![]() si solutiile
globale, pentru aceleasi valori, notate cu
si solutiile
globale, pentru aceleasi valori, notate cu ![]() ,
, ![]() si
si ![]() .
.
Determinati solutiile problemei
initiale ![]() .
.
Introducem functiile ![]() , iar
, iar ![]() . Asadar, functia
. Asadar, functia ![]() este continua pe
domeniul de definitie al ecuatiei
este continua pe
domeniul de definitie al ecuatiei
![]() .
.
Ecuatia ![]() are unica
radacina reala
are unica
radacina reala ![]() si deci,
exista o singura solutie
stationara
si deci,
exista o singura solutie
stationara
![]() ,
, ![]() .
.
Cum ![]() ,
, ![]() , rezulta ca
, rezulta ca ![]() nu este
marginita pe multimea
nu este
marginita pe multimea ![]() , deci nu verifica conditiile teoremei de
existenta si unicitate si atunci este de asteptat ca
in punctele de forma
, deci nu verifica conditiile teoremei de
existenta si unicitate si atunci este de asteptat ca
in punctele de forma ![]() ecuatia
diferentiala sa aiba solutii
singulare.
ecuatia
diferentiala sa aiba solutii
singulare.
Pe multimea ![]() , unde
, unde
![]() si
si ![]() ,
,
se pot separa variabilele si putem scrie ecuatia data sub urmatoarea forma
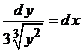 . (1)
. (1)
Pentru fiecare membru al ecuatiei (1) se determina cate o primitiva (se integreaza in ambii membrii ai ecuatiei) si se obtine relatia
![]() , (2)
, (2)
care defineste solutia
generala sub forma
implicita a ecuatiei (1) pe domeniul![]() . Rezolvand ecuatia (2) in raport cu
. Rezolvand ecuatia (2) in raport cu ![]() se determina, pe
se determina, pe ![]() , solutia
generala sub forma explicita
, solutia
generala sub forma explicita
![]() , (3)
, (3)
Asadar, ecuatia considerata are solutiile:
O solutie
stationara ![]() ,
, ![]() , care este solutie globala;
, care este solutie globala;
Pe multimea ![]() , unde
, unde ![]() ,
, ![]() , solutia generala este maximala si are
forma explicita
, solutia generala este maximala si are
forma explicita
![]() ,
, ![]() ;
;
Pe multimea ![]() , unde
, unde ![]() ,
, ![]() , solutia generala este de asemenea
, solutia generala este de asemenea
maximala si se expliciteaza sub forma
![]() ,
, ![]() .
.
In continuare vom analiza unicitatea solutiei problemei initiale.
Din conditia
initiala rezulta ca punctul ![]() este ales astfel incat
este ales astfel incat
![]() si deci solutiile
ecuatiei diferentiale care verifica conditia
initiala data pot sa nu fie unice. Astfel, solutia stationara
si deci solutiile
ecuatiei diferentiale care verifica conditia
initiala data pot sa nu fie unice. Astfel, solutia stationara ![]()
![]() , verifica conditia initiala si deci
este solutie a problemei Cauchy, aceasta fiind de fapt o solutie singulara a
ecuatiei diferentiale date (in orice punct al curbei integrale,
definita de aceasta solutie, nu se verifica conditiile
teoremei de existenta si unicitate; de exemplu, in punctele
, verifica conditia initiala si deci
este solutie a problemei Cauchy, aceasta fiind de fapt o solutie singulara a
ecuatiei diferentiale date (in orice punct al curbei integrale,
definita de aceasta solutie, nu se verifica conditiile
teoremei de existenta si unicitate; de exemplu, in punctele ![]() , functia
, functia ![]() nu este
marginita.
nu este
marginita.
Conform propozitiei 2, exista
o vecinatate ![]() a punctului
a punctului ![]() si o functie
si o functie
![]() , solutie locala a ecuatiei date (
, solutie locala a ecuatiei date (![]() , nu neaparat unica!) si care verifica
conditia initiala
, nu neaparat unica!) si care verifica
conditia initiala ![]() . De exemplu, functia
. De exemplu, functia ![]() ,
, ![]() , obtinuta din solutia generala pentru
valoarea constantei
, obtinuta din solutia generala pentru
valoarea constantei ![]() , este o solutie
locala care verifica conditia initiala. Mai mult,
curba integrala
, este o solutie
locala care verifica conditia initiala. Mai mult,
curba integrala ![]() , se intersecteaza cu solutia singulara (dreapta
, se intersecteaza cu solutia singulara (dreapta ![]() ) in punctul
) in punctul ![]() unde aceasta este
tangenta curbei integrale. (Este usor de vazut ca aceasta
functie poate fi obtinuta direct luand primitivele in ambii
membri ai relatiei (3.1): pentru
orice
unde aceasta este
tangenta curbei integrale. (Este usor de vazut ca aceasta
functie poate fi obtinuta direct luand primitivele in ambii
membri ai relatiei (3.1): pentru
orice ![]() si orice
si orice ![]() , avem
, avem
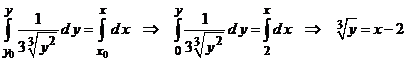 .
.
Atunci definim ![]() ,
, ![]() ).
).
Se constata ca pentru
punctul ![]() exista o
infinitate de solutii
exista o
infinitate de solutii ![]() care verifica
conditia initiala
care verifica
conditia initiala ![]() si care
prelungeste solutia locala. De exemplu, functiile
si care
prelungeste solutia locala. De exemplu, functiile
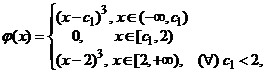 (4)
(4)
definite pentru fiecare ![]() , sunt continue si derivabile pe
, sunt continue si derivabile pe ![]() , satisfac conditia
, satisfac conditia ![]() si verifica
ecuatia diferentiala data.
si verifica
ecuatia diferentiala data.
Deci functiile (4) sunt solutii ale problemei initiale, care nu sunt nici solutii singulare si nici solutii particulare.
Observatie. In
fiecare punct al multimii![]() , apartinand curbei integrale (dreapta
, apartinand curbei integrale (dreapta ![]() ), definita de solutia singulara, exista
o infinitate de solutii ale ecuatiei diferentiale date, ale
caror curbe integrale trec prin fiecare din aceste puncte. Asa cum se
observa, solutia singulara nu se poate obtine din
solutia generala prin particularizarea constantei de integrare.
), definita de solutia singulara, exista
o infinitate de solutii ale ecuatiei diferentiale date, ale
caror curbe integrale trec prin fiecare din aceste puncte. Asa cum se
observa, solutia singulara nu se poate obtine din
solutia generala prin particularizarea constantei de integrare.
Din punct
de vedere geometric, curba integrala a solutiei singulare (dreapta ![]() ) este infasuratoarea familiei de curbe
integrale ale solutiei generale
) este infasuratoarea familiei de curbe
integrale ale solutiei generale ![]() ,
, ![]() .
.
Observatie.
Potrivit propozitiei 2, pentru orice punct ![]() (in
(in ![]() ,
, ![]() ) exista o vecinatate
) exista o vecinatate ![]() si o unica functie
si o unica functie ![]() , solutie locala
a ecuatiei cu variabile separabile (3.1) care verifica conditia
, solutie locala
a ecuatiei cu variabile separabile (3.1) care verifica conditia ![]() . Orice solutie locala poate fi prelungita
pana la o solutie globala (nu neaparat in mod unic (!)). De
exemplu, daca dorim sa determinam solutia care trece prin
punctul
. Orice solutie locala poate fi prelungita
pana la o solutie globala (nu neaparat in mod unic (!)). De
exemplu, daca dorim sa determinam solutia care trece prin
punctul ![]() , vom observa ca
, vom observa ca ![]() si atunci din (3)
putem determina pe
si atunci din (3)
putem determina pe ![]() o unica solutie
locala avand forma
o unica solutie
locala avand forma
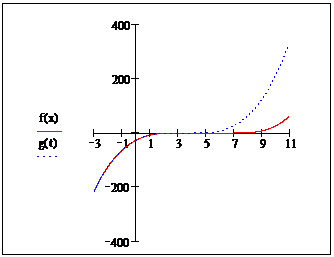
![]() ,
, ![]() . (5)
. (5)
Aceasta
solutie poate fi prelungita intr-o infinitate de moduri pe intervalul
![]() ; de exemplu, functia
; de exemplu, functia
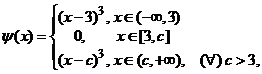
definita pentru fiecare ![]() fixat, este solutie maximala care
prelungeste solutia locala.
fixat, este solutie maximala care
prelungeste solutia locala.
In
figura alaturata graficul functiei ![]() reprezinta
graficul solutiei
reprezinta
graficul solutiei ![]() pentru valoarea constantei
pentru valoarea constantei
![]() egala cu
egala cu ![]() , iar graficul functiei
, iar graficul functiei ![]() coincide cu graficul
solutiei
coincide cu graficul
solutiei ![]() pentru valoarea
pentru valoarea ![]() .
.
2. Ecuatii diferentiale omogene (e.d.o.)
Definitie. Se numeste ecuatie diferentiala omogena o ecuatie de forma
![]() (2.16)
(2.16)
definita de functia continua ![]() care este omogena de gradul zero in raport cu
ambele variabile
care este omogena de gradul zero in raport cu
ambele variabile
Exemple Care din ecuatiile de mai jos sunt omogene?
![]() R. Este ecuatie
omogena:
R. Este ecuatie
omogena: ![]() .
.
![]() ;
;
R. Se
pune sub forma 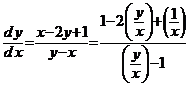 si se constata ca nu este
ecuatie omogena.
si se constata ca nu este
ecuatie omogena.
3). ![]() R. Este ecuatie omogena.
R. Este ecuatie omogena.
Se
stie ca functia ![]() este omogena de gradul
este omogena de gradul ![]() in raport cu ambele
variabile, daca
in raport cu ambele
variabile, daca
![]() si
si ![]() . (2.17)
. (2.17)
![]() (2.18)
(2.18)
si deci, functia
![]() poate fi
identificata cu o functie
poate fi
identificata cu o functie ![]() care este functie
continua.
care este functie
continua.
Asadar, ecuatia (2.16) poate fi scrisa sub forma
![]() (2.19)
(2.19)
unde ![]() este functie
continua pe
multimea
este functie
continua pe
multimea
![]() .
.
Ecuatia omogena (2.19) poate fi transformata intr-o ecuatie cu variabile separabile daca de face schimbarea de functie
![]() . (2.20)
. (2.20)
![]() si
si ![]() . (2.21)
. (2.21)
Cu notatia ![]() ,
, ![]() este
derivabila si
este
derivabila si
![]() ,
,
Rezulta ca
functia ![]() este solutie a
ecuatiei cu variabile separabile
este solutie a
ecuatiei cu variabile separabile
![]() (2.22)
(2.22)
si atunci, potrivit
teoriei e.d.v.s., functia ![]() se poate determina
abstractie facand de o
se poate determina
abstractie facand de o ![]() este determinata.
este determinata.
Reciproc,
orice solutie ![]() a ecuatiei cu
variabile separabile (2.22) genereaza o solutie a ecuatiei
omogene (2.19). Intr-adevar, daca
a ecuatiei cu
variabile separabile (2.22) genereaza o solutie a ecuatiei
omogene (2.19). Intr-adevar, daca ![]() este solutie a
ecuatiei cu variabile separabile, atunci avem
este solutie a
ecuatiei cu variabile separabile, atunci avem
![]()
si deci functia ![]() ,
verifica ecuatia omogena
,
verifica ecuatia omogena
![]() .
.
Pentru integrarea ecuatiilor omogene vom utiliza urmatorul algoritm
Pasul 1. Se efectuiaza schimbarea de
functie (2.20), adica pentru fiecare solutie ![]() a ecuatiei
omogene (2.19), schimbarea de functie (2.20) este
a ecuatiei
omogene (2.19), schimbarea de functie (2.20) este
![]() sau
sau![]()
![]() ,
,
deci ![]() este solutie a
ecuatiei cu variabile separabile (2.22).
este solutie a
ecuatiei cu variabile separabile (2.22).
Pasul 2. Se scrie ecuatia cu variabile separabile sub forma
![]() ,
,
Pasul 3. Se revine la schimbarea de functie, apoi se scriu solutiile ecuatiei omogene:
Solutiile
stationare ![]()
Solutia
generala 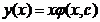 .
.
Exercitii
I. Sa se verifice care dintre ecuatiile de mai jos sunt ecuatii omogene si in caz afirmativ sa se integreze:
1). ![]() . 5).
. 5).
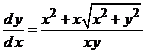 .
.
2). ![]() . 6).
. 6). ![]() .
.
3). ![]() . 7)
. 7) ![]() .
.
4). ![]() 8).
8). 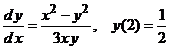 .
.
3. Ecuatii diferentiale de forma
![]() , (2.23)
, (2.23)
unde ![]() este functie continua
este functie continua
Daca
membrul drept al ecuatiei ![]() poate fi exprimat in
functie de combinatia
poate fi exprimat in
functie de combinatia ![]() , cu
, cu ![]() constante, atunci
schimbarea de functie
constante, atunci
schimbarea de functie
![]() , (2.24)
, (2.24)
transforma ecuatia data intr-o ecuatie cu variabile separabile.
Metoda integrarii acestui tip de ecuatii este prezentata prin exemplul urmator:
![]() .
.
Partea
dreapta a ecuatiei poate fi exprimata ca functie de ![]() , deci,
, deci,
![]() .
.
Fie
substitutia ![]() . Prin diferentiere obtinem relatia
. Prin diferentiere obtinem relatia ![]() sau echivalent
sau echivalent ![]() . Inlocuind in
ecuatia data, obtinem
. Inlocuind in
ecuatia data, obtinem
![]() sau
sau ![]() ,
,
care, evident, este o ecuatie cu variabile separabile. In urma separarii variabilelor, printr-o cuadratura, obtinem
![]()
![]() .
.
Asadar, solutia generala a e.d.v.s. are forma implicita
![]() .
.
Substituind
![]() prin
prin ![]() obtinem solutia generala ecuatiei
date sub forma implicita
obtinem solutia generala ecuatiei
date sub forma implicita
![]() .
.
Solutiile
stationare ale ecuatiei cu variabile separabile au forma ![]() ,
, ![]() pentru orice
pentru orice ![]() . Deci, ecuatia data are solutiile stationare:
. Deci, ecuatia data are solutiile stationare:
![]() ; si
; si ![]() .
.
Exercitii
Sa se integreze ecuatiile diferentiale:
1). ![]() .
.
2). ![]() .
.
3). ![]() .
.
4). ![]() cu conditia
cu conditia ![]() .
.
5). ![]() .
.
6). ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |