
Analiza datelor experimentale - modele probabilistice
Cautarea unor modele probabilistice care sa aproximeze satisfacator diverse fenomene cu caracter aleatoriu a condus la identificarea de diverse distributii. Cele mai uzuale distributii folosite in domeniul telecomunicatiilor sunt: distributia Bernoulli, distributia binomiala, distributia geometrica, distributia Poisson, distributia gaussiana (normala), distributia exponentiala, distributia gama, distributia Pareto, distributia c , distributia m-Erlang etc.
Pentru identificarea
modelului matematic care aproximeaza cel mai bine un anumit experiment se
recurge totdeauna la analiza si interpretarea rezultatelor experimentale,
folosind diverse metode, care sunt fie de natura calitativa, cum este
metoda histogramei, fie de natura cantitativa, cum sunt testele ![]() si Kolmogorov-Smirnov
si Kolmogorov-Smirnov
In acest capitol voi
prezenta testele ![]() (Chi patrat) si Kolmogorov-Smirnov, folosite in capitolele anterioare pentru potrivirea
seturilor de date cu diferite distributii.. Pentru aceasta analiza este nevoie sa
cunoastem elementele de interes doar pentru
cateva dintre ele. Aceste elemente sunt expuse in tabelul 1
(Chi patrat) si Kolmogorov-Smirnov, folosite in capitolele anterioare pentru potrivirea
seturilor de date cu diferite distributii.. Pentru aceasta analiza este nevoie sa
cunoastem elementele de interes doar pentru
cateva dintre ele. Aceste elemente sunt expuse in tabelul 1
Tabelul 1 Elemente ale distributiilor etalon
|
Parametri |
Medie |
Varianta
|
pdf / probabilitati elementare |
|
|
Distributia exponentiala |
|
|
|
|
|
Distributia gama |
|
|
|
|
|
Distributia gaussiana (normala) |
|
|
|
|
|
Distributia binomiala |
|
|
|
|
|
Distributia Poisson |
|
|
|
|
|
Distributia geometrica |
|
|
|
|
1 Testul Kolmogorov-Smirnov
Testul Kolmogorov-Smirnov, notat prin K-S, opereaza asupra diferentelor ce apar intre functia empirica, de distributie, obtinuta pe baza unui esantion de rezultate si functia analitica luata in considerare. Din acest motiv, testul K-S se preteaza doar situatiilor in care functia analitica de distributie este continua.
Fie o variabila aleatorie continua cu o distributie necunoscuta
![]() si o functie
de distributie ipotetica CDF ce pare a fi asemanatoare cu
distributia variabilei de analizat. Se doreste testarea ipotezelor:
si o functie
de distributie ipotetica CDF ce pare a fi asemanatoare cu
distributia variabilei de analizat. Se doreste testarea ipotezelor:
- ![]() : variabila
: variabila ![]() are distributia CDF, adica
are distributia CDF, adica ![]() pentru
orice
pentru
orice ![]()
- ![]() : variabila
: variabila ![]() nu are distributia CDF, adica
nu are distributia CDF, adica ![]() cel putin pentru un
cel putin pentru un ![]() .
.
In cele ce urmeaza voi stabili functia de distributie a probabilitatilor pentru durata de ocupare a unui canalul de transmisiuni Voi face analiza datelor experimentale cu ajutorul testului Kolmogorov-Smirnov, considerand ca functii etalon distributiile gauss-normala, exponentiala si gama. Pentru aceasta am realizat un program in matlab ce realizeaza testarea ipotezelor. Am urmarit pasii:
- Am "incarcat " datele experimentale si am sortat datele in ordine crescatoare, rezuland astfel vectorul x..
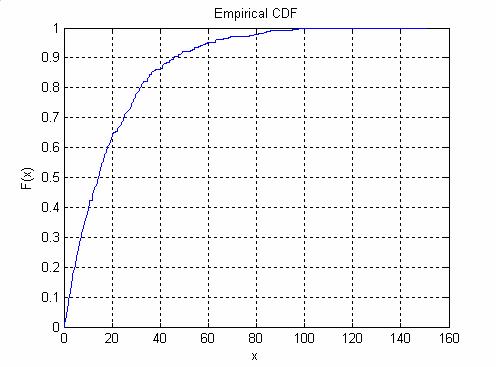
Fig. 2 Distributia empirica
- Se
executa testul K-S, pentru fiecare functie de distributie etalon,
considerand implicit nivelul semnificativ (![]()
Tabelul 2 Rezultatele simularii
|
Distributia exponentiala |
Distributia gauss normala |
Distributia gamma | ||
|
Ipoteza H | ||||
|
valoarea p |
2,4069e-009 | |||
|
d | ||||
|
Deviatia critica tα |
Tabelul 2 contine valorile parametrilor simulati pentru
testarea ipotezei ![]()
Testarea
ipotezei se face prin intermediul unei 'statistici', o valoare ![]() rezultata in urma
unui calcul ce ia in considerare un anumit esantion de rezultate.
rezultata in urma
unui calcul ce ia in considerare un anumit esantion de rezultate.
Luand in
considerare valoarea ![]() si ipoteza
si ipoteza ![]() se poate calcula o
valoare, numita "valoare p' (p value) , care exprima gradul de
credibilitate al ipotezei. Concret, valoarea
p este probabilitatea ca, in conditiile considerarii ipotezei
se poate calcula o
valoare, numita "valoare p' (p value) , care exprima gradul de
credibilitate al ipotezei. Concret, valoarea
p este probabilitatea ca, in conditiile considerarii ipotezei ![]() adevarate,
statistica unui esantion oarecare de rezultate,
adevarate,
statistica unui esantion oarecare de rezultate, ![]() ,
sa fie cel putin egala cu statistica esantionului curent de
rezultate
,
sa fie cel putin egala cu statistica esantionului curent de
rezultate ![]() .
.
Marimea
![]() reprezinta deviatia critica a carei
valoare depinde de nivelul probabilistic semnificativ si de dimensiunea
esantionului de rezultate.
reprezinta deviatia critica a carei
valoare depinde de nivelul probabilistic semnificativ si de dimensiunea
esantionului de rezultate.
Asfel, urmarind pasii testului K-S putem trage urmatoarele concluzii:
- Ipoteza ![]() este acceptata
pentru distributiile exponentiala si gamma. Aceasta se
observa clar deoarece in cazul acestor distributii valoarea p este
mai mare decat nivelul probabilistic semnificativ,
este acceptata
pentru distributiile exponentiala si gamma. Aceasta se
observa clar deoarece in cazul acestor distributii valoarea p este
mai mare decat nivelul probabilistic semnificativ, ![]() , si in acelasi timp deviatia critica este mai mare decat
valoarea
, si in acelasi timp deviatia critica este mai mare decat
valoarea ![]() ,
conditii necesare pentru acceptarea ipotezei.
,
conditii necesare pentru acceptarea ipotezei.
- In cazul distributiei gauss normala
ipoteza ![]() este respinsa,
deoarece nu este indeplinita nici una din conditiile de acceptare a
ipotezei.
este respinsa,
deoarece nu este indeplinita nici una din conditiile de acceptare a
ipotezei.
- Am trasat suprapus peste curba anterioara cele trei functii teoretice de distributie pentru analiza comparativa
Desi ne putem da seama din valorile parametrilor ce distributie se potriveste mai bine cu cea emiprica este mai convenabila examinarea vizuala a diagramei deviatiei pentru curba suprapusa. Figura 3 reprezinta diagrama curbelor pentru distributia datelor experimentale si distributiile etalon (distributiile exponentiala, normala si gamma).
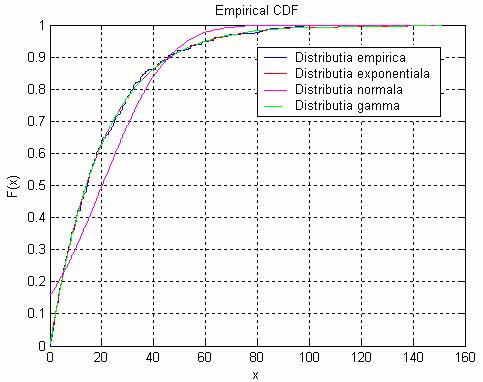
Fig 3 Reprezentarea grafica a curbelor corespunzatoare distributiei empirice si distributiilor etalon.
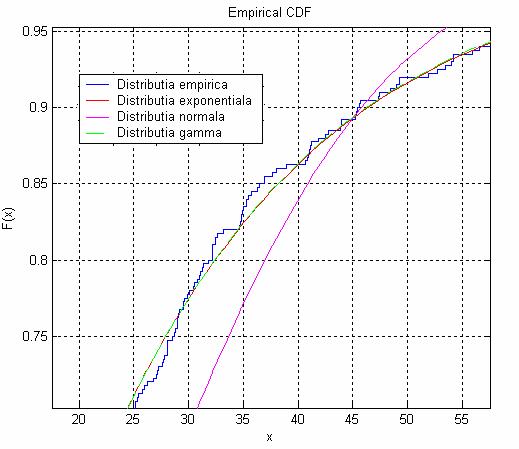
Fig. 4: Reprezentarea cu zoom a curbelor corespunzatoare distributiei empirice si distributiilor etalon
In figurile 3 si 4 observam
potrivirea dintre distributiile exponentiala si gama,
precum si nepotrivirea cu distributia gauss. Din grafic se
observa si asemanarea dintre distributiile gama si
exponentiala, motiv pentru care ambele se potrivesc cu cea
empirica. Din tabelul 1 observam ca distributia
exponentiala este un caz particular al distributiei gama. In
cazul distributiei gama pentru ![]() se obtine
distributia exponentiala.
se obtine
distributia exponentiala.
2 Testul Chi-patrat![]()
Testul ![]() este o metoda
cantitativa, pe baza careia, in urma efectuarii unor calcule, se
decide acceptarea sau respingerea ipotezei presupuse a caracteriza fenomenul
aleatoriu studiat
este o metoda
cantitativa, pe baza careia, in urma efectuarii unor calcule, se
decide acceptarea sau respingerea ipotezei presupuse a caracteriza fenomenul
aleatoriu studiat
Am realizat un program pentru a determina modelul matematic care descrie in mod adecvat procesul sosirilor, exprimat prin numar de sosiri la fiecare 100 ms. Am parcurs urmatorii pasi:
- Am stabilit durata intervalului de referinta la 100ms. Numarul observat de sosiri, arriv_no, pe fiecare interval succesiv se reprezinta grafic pentru a vizualiza realizarea particulara, observata, a procesului analizat (Figura 6).
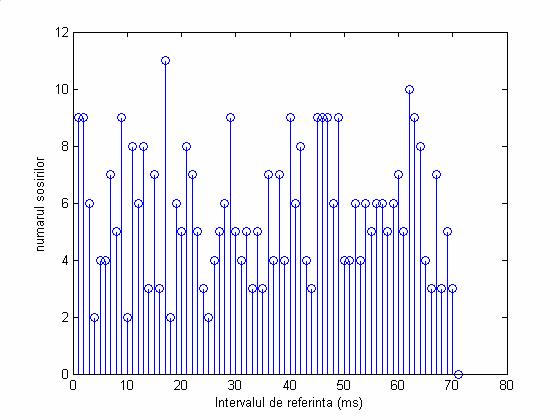
Fig. 6 Numarul sosirilor pe fiecare interval succesiv in parte
- Urmatorul pas consta in stabilirea plajei de variatie, anume vectorul k, a numarului de sosiri pe un interval dat, cuprinsa intre si valoarea maxima din vectorul dat de numarul sosirilor, incrementata cu 1. Am definit inca un vector ce reprezinta numarul observat de intervale, cu acelasi numar de sosiri si se calculeaza elementele acestui vector. Astfel conform figurii 6 in 4 intervale s-au inregistrat cate 2 sosiri. Valoarea vectorului este urmatoarea:
k_interv_no 0 4 9 11 11 11 7 5 10 1 1 0]
- Am luat in considerare drept ipoteze posibile distributiile teoretice Poisson, geometrica si binomiala. Pentru fiecare se calculeaza valorile parametrilor asociati si apoi se calculeaza vectorii probabilitatilor corespunzatoare acestor distributii teoretice(ppois, pgeo si pbin) in punctele continute in vectorul k. Am obtinut urmatoarele valori:
ppois = [ 0.0036 0.0201 0.0567 0.1065 0.1501 0.1691 0.1588 0.1278 0.0900
0.0563 0.0317 0.0163 0.0076]
pgeo = NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
pbin = [0.0033 0.0191 0.0550 0.1052 0.1502 0.1707 0.1609 0.1295 0.0907
0.0563 0.0313 0.0157 0.0072]
Se observa ca pentru punctele continute in vectorul k pentru distributia geometrica nu ia valori. In figura 7 observam valorile pentru distributia poisson si binomiala.
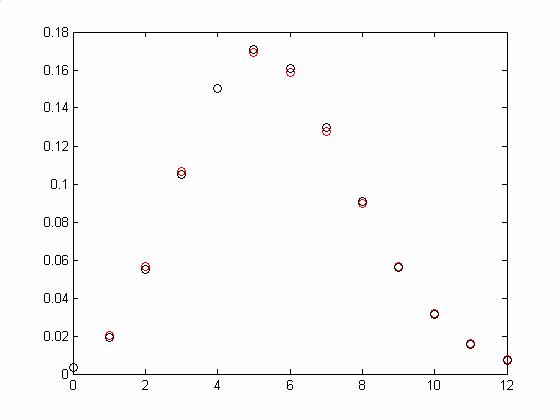
Fig. 7. Probabilitatile distributiilor teoretice in punctele vectorului k
Pentru fiecare distributie, se calculeaza apoi vectorul numarului asteptat de intervale cu acelasi numar de sosiri ( narriv_pois, narriv_geo si narriv_bin). Am pbtinut urmatoarele valori:
nariv_pois = [0.2538 1.4300 4.0281 7.5645 10.6543 12.0048 11.2721 9.0721 3888 3.9993 2.2531 1.1540 0.5418]
nariv_geo = NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
nariv_bin = [0.2345 1.3568 3.9080 7.4703 10.6620 12.1191 11.4274 9.1939 4428 3.9948 2.2190 1.1153 0.5115]
- Pentru aprecierea calitativa a asemanarii dintre rezultatele asteptate si cele observate se deseneaza, pe acelasi grafic, histogramele corespunzatoare. Matricea p are drept coloane vectorii numerelor asteptate si observate de intervale cu acelasi numar de sosiri.
p =
NaN 0.2345 1.0000
NaN 1.3568 0
NaN 3.9080 4.0000
NaN 7.4703 9.0000
NaN 10.6620 11.0000
NaN 12.1191 11.0000
NaN 11.4274 11.0000
NaN 9.1939 7.0000
NaN 4428 5.0000
NaN 3.9948 10.0000
NaN 2.2190 1.0000
NaN 1.1153 1.0000
NaN 0.5115 0
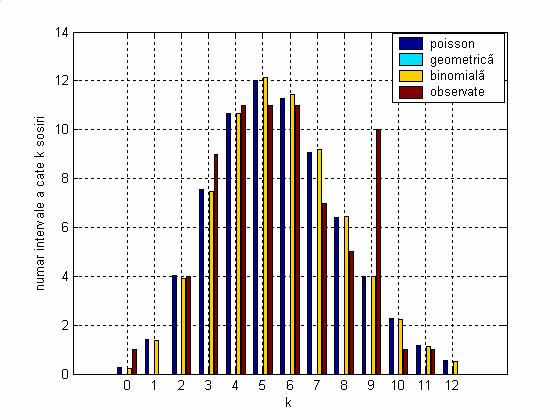
Fig 8 Asemanarea dintre rezultatele asteptate si cele observate
- Executarea testului Chi patrat: pentru aprecierea cantitativa si luarea deciziei finale se calculeaza statistica testului chi patrat pentru fiecare ipoteza in parte, (dpois, dgeo si dbin).
Se obtin urmatoarele valori:
dpois =15.0363
dbin =15.3682
dgeo =NaN
Pentru a lua o decizie aceste valori sunt comparate cu deviatia critica, data de tabelul 3.
Tabelul 3:
Deviatii critice, ![]() , functie de nivelul probabilistic semnificativ,
, functie de nivelul probabilistic semnificativ, ![]() ,
,
si de numarul de intervale, ![]()
|
|
| ||||
|
|
|
|
|
||
|
| |||||
Pentru un nivel probabilistic semnificativ de
0,05 deviatia critica pentru k=12 este 19.68. Ipoteza ![]() este acceptata daca
statistica chi este mai mica sau egala cu deviatia critica.
Am observat ca sunt acceptate si distributia poisson si cea
binomiala. Acest lucru se intampla deoarece distributia poisson aproximeaza distributia
binomiala pentru
este acceptata daca
statistica chi este mai mica sau egala cu deviatia critica.
Am observat ca sunt acceptate si distributia poisson si cea
binomiala. Acest lucru se intampla deoarece distributia poisson aproximeaza distributia
binomiala pentru ![]() 'mic'
si
'mic'
si ![]() 'mare',
considerand:
'mare',
considerand: ![]() .(tabelul 1)
.(tabelul 1)
Anexa
Program pentru divizarea ariei de serviciu:
t=random('unid',150,14,11)*0.1
s=sum(sum(t))/2
sc1=sum(t,1);
sc2(1)=sc1(1);
for j=2:11;
sc2(j)=sc2(j-1)+sc1(j);
end
%sc2
dc1=abs(sc2-s)
[min_c,c1]=min(dc1)
c1
for i=1:14
for j=1:11
if j<=c1
a(i,j)=t(i,j);
b(i,j)=0;
else a(i,j)=0;b(i,j)=t(i,j);
end
end
end
a
b
sL1a=sum(a,2);
sL2a(1)=sL1a(1);
for i=2:14
sL2a(i)=sL2a(i-1)+sL1a(i);
end
%sL2a
dLa=abs(sL2a-s/2)
[min_L,La1]=min(dLa)
sL1b=sum(b,2);
sL2b(1)=sL1b(1);
for i=2:14
sL2b(i)=sL2b(i-1)+sL1b(i);
end
%sL2b
dLb=abs(sL2b-s/2)
[min_L,Lb1]=min(dLb)
Testul K-S
clear all
r = load ('data1.txt')
cdfplot(r)
grid
hold
x=sort(r)
mu=mean(r)
sigma=std(r)
y1=expcdf(x,mu);
y2=normcdf(x,mu,sigma);
a=(mu/sigma)^2
b=mu/a;
y3=gamcdf(x,a,b);
plot(x,y1,'r',x,y2,'m',x,y3,'--g')
grid
[h1,p1,d1,ta1] = kstest(x,[x y1])
[h2,p2,d2,ta2] = kstest(x,[x y2])
[h3,p3,d3,ta3] = kstest(x,[x y3])
Testul Chi
%testul chi
clear all
r = load ('data2.txt');
%STABILIREA VALORILOR OBSERVATE
%durata intevalului de referinta:
lapse=100;%msec
%vectorul capetelor de interval:
z=0:lapse:lapse*ceil(max(r)/lapse);
%numarul de sosiri in fiecare interval
ariv_no=histc(r,z)
figure(1),stem(ariv_no)
%domeniul in care procesul ia valori
k=0:max(ariv_no)+1
%numar de intervale cu acelasi numar de sosiri
k_interv_no=histc(ariv_no,k)
%STABILIREA VALORILOR ASTEPTATE
%media numarului de sosiri pe un interval lapse
m=mean(ariv_no)%pentru experimental
v=std(ariv_no)^2
%calcul parametri distributii teoretice
p_bin=1-v/m;
n_bin=round(m/p_bin);
p_geo=m/v;
a_pois=m;
%probabilitati
ppois=pdf('poiss',k,a_pois)
%sum(ppois);
pgeo=pdf('geo',k,p_geo)
%sum(pgeo);
pbin=pdf('bino',k,n_bin,p_bin)
%sum(pbin)
figure(2),plot(k,ppois,'or',k,pgeo,'*b',k,pbin,'ok')
%numarul intervalelor considerate
interv_no=length(ariv_no);
%numarul intervalelor cu k sosiri asteptate
nariv_pois=interv_no.*ppois
nariv_geo=interv_no.*pgeo
nariv_bin=interv_no.*pbin
%TRASAREA HISTOGRAMELOR
p=[nariv_pois' nariv_geo' nariv_bin' k_interv_no]
figure(3),bar(k,p)
xlabel('k')
ylabel('numar intervale a cate k sosiri')
grid
%EXECUTAREA TESTULUI CHI2
dpois=sum((k_interv_no'-nariv_pois).^2./nariv_pois)
dbin=sum((k_interv_no'-nariv_bin).^2./nariv_bin)
dgeo=sum((k_interv_no'-nariv_geo).^2./nariv_geo)
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |