Rentabilitatea valorilor mobiliare
Cumpararea unei valori mobiliare (actiune, obligatiune, certificat de depozit etc.) reprezinta un aaact de investitie de capital. In fapt, este vorba de un transfer de un transfer de capital catre un antreprenor (catre o firma) de la care sse steapta o rentabilitate corespunzatoare riscului asumat prin aceasta investitie de capital propriu.
Teoria financiara moderna a formalizat un obiectiv complex al gestiunii valorilor mobiliare, si anume optimizarea corelatiei dintre rentabilitate si risc in plasarea capitalurilor financiare. Aceasta noua preocupare este tot mai necesara, in conditiile unei volatilitati sporite a valorilor mobiliare, in raport cu variatiile fenomenelor economice si financiare, ceea ce determina o relatie directa intre rentabilitate si risc. Cu alte cuvinte, o rentabilitate mare este insotita de un risc mai mare si vice-versa. Spre exemplu, investirea de capital in cumpararea unor obligatiuni cu dobanda de 4%, in termeni reali, realizeaza o rentabilitate mediocra, dar cu un risc scazut. Dimpotriva, investirea aceluiasi capital in cumpararea unor actiuni cu dividende variabile, ce a inregistrat anterior valori superioare celei de 4%, este insotita de un risc mult mai mare:
De realizare, in viitor, a unei rentabilitati mai mici de 4%;
De faliment si
De pierdere 100% a capitalului investit.
Rentabilitatea unei actiuni este determinata de doua componente ale castigului, intr-o astfel de investitie: dividendul si cresterea valorii de piata (castig de capital). Motivatia investitorului de a cumpara o actiune, imediat dupa emisiunea ei, este dividendul net pe care il va aduce aceasta actiune. Dar orice actiune necesita interesul investitorului si pentru o alta componenta a rentabilitatii si anume cresterea previzibila e valorii de piata in raport cu pretul ei de achizitie. Aceasta ultima motivatie este cea care determina o circulatie bursiera mai mult sau mai putin activa a actiunilor, in functie de castigul scontat prin speculatia bursiera. Asadar, rentabilitatea unei actiuni cuprinde dividendul net la sfarsitul perioadei de previziune (D1) si diferenta de curs dintre pretul viitor de piata (P1) si pretul de achizitie (P0) al respectivei actiuni. Deci, rentabilitatea (x, 'return') si (R) rata rentabilitatii unei actiuni se pot determina astfel:
X = D1 + P1 - P0
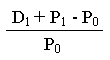
Consideratii similare se pot face si in legatura cu rentabilitatea unei obligatiuni. Astfel,daca obligatiunea din exemplul de mai sus, in valoarea nominala de1000 u.m. (pret de achizitie), are o crestere a pozitiei la bursa cu 6,25% (in termeni reali) fata de momentul achizitiei, atunci rentabilitatea si rata rentabilitatii acesteia sunt urmatoarele:
X = ( 0,04 + 0,0625 ) × 1000 = 102,5 lei ( in preturi constante)
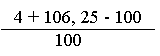
R = ×100 = 10,25%
In fapt, relatia de calcul nu este altceva decat formalizarea intentiei de fructificare a capitalului economisit si investit in cumpararea respectivei valori mobiliare. In raport cu pretul platit initial, investitorul asteapta o remunerare (R) care sa-i permita la sfarsitul perioadei de detinere a acesteia, incasarea unui devidend sau dobanda (D1) si recuperarea capitalului investit (la un pret de revanzare P1, pe cat posibil mai mare decat cel initial):
P0 ( 1 + R ) = D1 + P1
P0 R = D1 + P1 - P0,
de unde rezulta usor relatia de mai sus a ratei rentabilitatii:
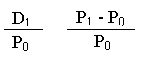
R = +
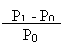
Deci, rata de rentabilitate a unui activ financiar este data de
remunerarea D1 / P0 pe care emitentul o poate asigura
investitorului de capital si de cresterea relativa, in timp, a valorii
activuliu respectiv
In termeni concreti, R semnifica fructificarea unui bun investit in cumpararea titlului respectiv.
Seria statistica poate fi compusa din ratele rentabilitatii inregistrate lunar, saptamanal sau la fiecare sedinta. Pe baza frecventelor absolute de aparitie se calculeaza frecventele relative. Pentru a studia speranta matematica de a realiza in viitor o anumita rentabilitate este necesara studierea legii probabilitatii care modeleaza cel mai bine repartitia ratelor de rentabilitate. Numeroase studii efectuate pe baza unor serii statistice de date au condus la concluzia ca, legea de repartitie care aproximeaza foarte bine distributia ratelor rentabilitatii este legea normala. Pe baza acestora, se poate calcula speranta matematica de obtinere a rentabilitatii, prin determinarea valorii medii a rentabilitatii individuale, astfel:
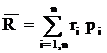
Unde ri si pi sunt rata rentabilitatii, respectiv probabilitatea ei de aparitie la momentul i, iar n este numarul de observatii statistice.
Calculul ratei anuale de rentabilitate
Rentabilitatea calculata mai sus vizeaza intreaga perioada de detinere a valorii mobiliare cumparate (cateva luni sau cativa ani). Pentru comparabilitatea ei cu rate de dobanda din economie este necesara anualizarea ratei de rentabilitate. Altfel spus, trebuie cautata rata anuala (interna) de rentabilitate (Ra) care a condus la obtinerea unei rate totale (RT) aferente intregii perioade de detinere a titlului si deci, a creantei antreprenorului, firmei:
( 1 + Ra )T = 1 + RT,
in care T este numarul de ani sau de fractiuni de ani de detinere a titlului.
Din relatia de mai sus se extrage usor Ra ca solutie a ecuatiei de ordin superior astfel exprimata:
![]()
Presupunand ca obligatiunea din exemplul precedent a fost pastrata timp de doi ani pana la revanzarea sau rascumpararea ei, atunci rata ei anuala de dobanda, in termeni reali, este:
![]()
Oare media geometrica este cea mai buna exprimare a rentabilitatii asteptate pentru un proiect de investitie ? Este aceasta mai corecta decat media aritmetica, stind ca aceasta din urma este mai mare sau cel mult egala cu media geometrica ? Paradoxal, media aritmetica este o estimare mai buna a rentabilitatii sperate a unei investitii decat media geometrica. Si aceasta pentru ca, statistic, media aritmetica a unui esantion este o estimare pertinenta a mediei populatiei analizate.
In acelasi exemplu al obligatiunii detinute timp de doi ani, rata medie de rentabilitate este de 5,125 % > 5 % :
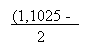
R - = 0,05125 = 5,125 %
Exprimarea rentabilitatii in termeni nominali (in preturi curente) presupune luarea in calcul a ratei inflatiei, conform amintitei relatiei a 'efectului Fisher'.
1 + Rn = (1 + Rr) (1 + i), pentru un an
(1 + Rn)2 = (1 + Rr)2 (1 + i)2 , pentru doi ani
In cazul tarii noastre, Banca Nationala a Romaniei anticipeaza in urmatorii doi ani o rata anuala a inflatiei de circa 25%. Rata de rentabilitate si rentabilitatea absoluta, in termeni nominali, ale obligatiunii noastre vor fi:
Ran = (1 + 0,05) (1 + 0,25) - 1 = 0,3125 = 31,25 %
Rn = (1 + 0,05) (1 + 0,25) 2 - 1 = 0,722656 = 72,2656 %
Xn = 0,722656 1000 = 722,656 lei (in preturi curente ale anului al doilea)
![]()
![]() In
termeni investitionali, ceea ce intereseaza este rentabilitatea (R) scontata,
cea asteptata din detinerea activului financiar respectiv. Determinarea ei
presupune o estimare a fluxurilor viitoare de venituri ce vor fi degajate de
societatea emitenta. Cel mai adesea se apeleza, insa, la o extrapolare
statistica a rentabilitatilor anterioare. Se retine, ca ipoteza de lucru, ca in
viitor tendinta se va pastra, relativ in aceiasi parametri. De aceea, cea mai
buna masura a rentabilitatii viitoare este media (R) a rentabilitatilor
inregistrate anterior (Rt):
In
termeni investitionali, ceea ce intereseaza este rentabilitatea (R) scontata,
cea asteptata din detinerea activului financiar respectiv. Determinarea ei
presupune o estimare a fluxurilor viitoare de venituri ce vor fi degajate de
societatea emitenta. Cel mai adesea se apeleza, insa, la o extrapolare
statistica a rentabilitatilor anterioare. Se retine, ca ipoteza de lucru, ca in
viitor tendinta se va pastra, relativ in aceiasi parametri. De aceea, cea mai
buna masura a rentabilitatii viitoare este media (R) a rentabilitatilor
inregistrate anterior (Rt):
![]()
![]()
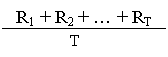
R = = a Rt
In care R1 , R2 , ., RT sunt rate anuale de rentabilitate efectiv inregistrate anterior;
t = 1, 2, .T reprezinta anul in care s-a inregistrat rata anuala de rentabilitate.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |