Tehnologie Afaceri Scoala Didactica Legislatie Familie

Acasa » scoala » fizica
Centrul de greutate al unui sistem de puncte materiale

Centrul de greutate al unui sistem de puncte materiale

Centrul de greutate al unui sistem de puncte materiale

Se considera un sistem de puncte materiale () de greutati , ai caror vectori de pozitie in raport cu un sistem de referinta sunt. Greutatile punctelor materiale formeaza un sistem de forte paralele , care este echivalent cu o rezultanta unica , numita greutatea sistemului de puncte materiale , egala cu suma greutatilor punctelor materiale :

G = a G_i )

  Greutatea sistemului este aplicata intr-un punct numit centru de greutate care se identifica cu centrul fortelor paralele C . Vectorul de pozitie al centrului de greutate se poate exprima sub forma :

 

Inlocuind G_i = m_i g , obtinem :

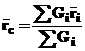
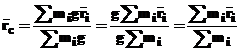Din analiza relatiei ( 3 ) se constata ca pozitia centrului de greutate nu depinde de

intensitatea campului gravitational terestru ,ci depinde numai de distributia maselor , motiv pentru care se numeste centrul de masa . Proiectand ecuatia ) pe axele Ox , Oy , Oz se obtin relatii de calcul ale coordonatelor centrului de masa ( greutate ) :

 

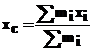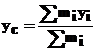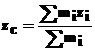Expresiile de forma, , se numesc momente statice ale sistemului de puncte materiale in raport cu planele yOz, xOz , xOy , si se noteaza S_x S_y S_z .

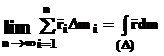iar expresiile : , , se vor numi momente statice ale rigidului in raport cu planele yOz , xOz si xOy .

Deci momentele statice caracterizeaza modul de distribuire a masei unui sistem de puncte materiale sau rigide . Momentele statice pot fi calculate fata de un plan , o axa sau un punct .

Deoarece masa sistemului M = a m_i , atunci relatiile ( 4 ) devin :

Observatii

Relatiile ( 6 ) exprima teorema momentelor statice : " momentul static al unui sistem de puncte materiale in raport cu un plan sau o axa este egal cu produsul dintre masa intregului sistem si distanta la acel plan sau acea axa " .

Relatiile ( 6 ) conduc la concluzia ca daca momentul static al unui sistem material in raport cu un plan sau o axa este nul , atunci centrul de masa se gaseste situat pe acel plan , respectiv pe acea axa .

.com	Copyright © 2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational.