Cinematica punctului material
Mecanica are ca parti importante cinematica, dinamica si statica.
Cinematica se ocupa cu studiul miscarii corpurilor, fara sa tina cont de interactiunile acestora cu exteriorul. Daca distantele pe care se misca corpul sunt mult mai mari decat dimensiunile acestuia, atunci putem considera corpul ca un punct material. Punctul material reprezinta un model in fizica, acest model presupunand ca un corp se misca asemeni unui punct material in care este concentrata toata masa acestuia.
Fie deci un punct material M care efectueaza o miscare dupa
curba C si care in timpul infinitezimal dt parcurge pe curba (C ) distanta ds,
careia ii corespunde o variatie a lui ![]() egala cu
egala cu ![]() , ca in figura 1.6.
, ca in figura 1.6.
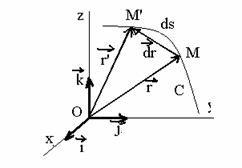
Figura 1.6 Parcursul ds si variatia lui ![]()
Curba (C ) reprezinta traiectoria punctului material M.
Scopul cinematicii este precizarea pozitiei si vitezei punctului material in orice moment de timp. Starea mecanica a unui corp este complet determinata daca se cunosc aceste marimi. Pentru a determina acesta stare, cinematica foloseste ecuatii de miscare, care exprima dependenta de timp a coordonatelor, a componentelor vitezei corpului sau a acceleratiei. In aceste ecuatii de miscare sunt implicate deci vectorul de pozitie, vectorul viteza si vectorul acceleratie. Aceste marimi sunt definite astfel :
vectorul de
pozitie ![]()
![]() (1.9)
(1.9)
vectorul
viteza ![]()
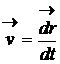 (1.10)
(1.10)
- vectorul acceleratie ![]()
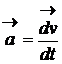 (1.11)
(1.11)
Pentru vectorul viteza, daca tinem cont de parcursul elementar ds pe traiectorie, avem :
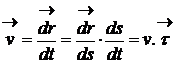 (1.12)
(1.12)
unde 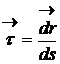 reprezinta un
vector tangent la traiectorie si care are modulul egal cu 1,
adica
reprezinta un
vector tangent la traiectorie si care are modulul egal cu 1,
adica ![]() este un versor.
Acesta poarta numele de versor
tangent. Faptul ca viteza ca vector poate fi scrisa ca in (1.12) cu ajutorul versorului
este un versor.
Acesta poarta numele de versor
tangent. Faptul ca viteza ca vector poate fi scrisa ca in (1.12) cu ajutorul versorului ![]() ne arata ca
viteza este un vector totdeauna tangent la traiectorie.
ne arata ca
viteza este un vector totdeauna tangent la traiectorie.
Pentru
acceleratie, urmand un rationament similar vom scrie 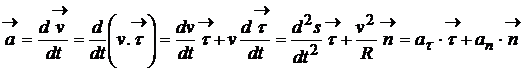 (1.13)
(1.13)
Aici in (1.13) am folosit relatia :
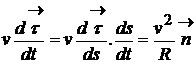 (1.14)
(1.14)
unde 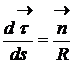 , cu
, cu ![]() care se numeste versor
normal iar R raza de curbura in punctul respectiv a
traiectoriei. Din (1.13) putem observa
ca acceleratia este un vector care are doua componente, o
componenta tangentiala
care se numeste versor
normal iar R raza de curbura in punctul respectiv a
traiectoriei. Din (1.13) putem observa
ca acceleratia este un vector care are doua componente, o
componenta tangentiala ![]() , numita
asa pentru ca ea este tangenta la traiectorie si o
componenta normala la curba
, numita
asa pentru ca ea este tangenta la traiectorie si o
componenta normala la curba ![]() , a carei
orientare este descrisa de versorul
, a carei
orientare este descrisa de versorul ![]() numit versor normal.
numit versor normal.
Pentru
a demonstra orientarea vectorilor viteza si acceleratie s-au
folosit versorii ![]() si
si ![]() . Se poate introduce si un al treilea versor, numit versor binormal
. Se poate introduce si un al treilea versor, numit versor binormal ![]() , definit astfel
, definit astfel
![]() (1.15)
(1.15)
Cei
trei versori ![]() formeaza un
triedru drept numit triedrul lui Frenet.
formeaza un
triedru drept numit triedrul lui Frenet.
In functie de valorile vectorului viteza si acceleratie putem avea :
a) Miscari uniforme
: ![]() = constant
= constant
b) Miscari uniform variate
: ![]() = constant
= constant
c) Miscari variate: ![]() = variabil
= variabil
iar in functie de forma curbei (C ) , deci a traiectoriei putem avea
a) miscari rectilinii
b) miscari curbilinii
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| PRIMUL PRINCIPIU AL TERMODINAMICII |
| CELE PATRU NIVELE STRUCTURALE ALE |
| Germinarea eterogena |
| Materia - Starile materiei |
| Lucrul mecanic |
| Legile generale ale spatiului si vitezei |
| Energia cinetica |
| Lucrul pV |
| Termeni si conditii |
| Contact |
| Creeaza si tu |