
Ecuatia macroscopica a miscarii fluidelor perfecte. Teorema impulsului
Prin integrarea ecuatiei (5.2) pe un volum V, marginit de o suprafata S de arie A, se obtine ecuatia macroscopica a miscarii, care exprima teorema propriu-zisa a impulsului.
Multiplicand ecuatia (5.2) cu dV si integrand-o pe volumul V se obtine
![]() (5.5)
(5.5)
Impulsul fluidului din volumul V este
![]() (5.6)
(5.6)
deci membrul stang al ecuatiei (5.5) reprezinta variatia
in timp a impulsului masei de fluid din volumul V, ![]() . Pe de alta parte, se poate scrie
. Pe de alta parte, se poate scrie
![]()
![]()
si tinand seama ca, din ecuatia (4.29), se poate
inlocui ![]() cu
cu ![]() , expresia de mai sus devine
, expresia de mai sus devine
![]() (5.7)
(5.7)
Inlocuind relatia (5.7) in membrul stang al ecuatiei (5.5), rezulta egalitatea
![]()
![]()
unde s-a transformat integrala de volum in integrala de
suprafata prin folosirea teoremei lui Gauss, considerand ca normala ![]() este orientata de
la exteriorul catre interiorul elementului de volum studiat.
este orientata de
la exteriorul catre interiorul elementului de volum studiat.
Ca urmare, se poate scrie
![]() (5.8)
(5.8)
Cele doua integrale din membrul drept al ecuatiei (5.5) pot fi scrise sub forma
![]()
unde s-a tinut seama, pentru prima egalitate, ca acceleratia
![]() a campului
fortelor masice este egala, in camp gravitational, cu
acceleratia gravitationala
a campului
fortelor masice este egala, in camp gravitational, cu
acceleratia gravitationala ![]() , iar pentru cea de a
doua, ca presiunea are directia normalei
, iar pentru cea de a
doua, ca presiunea are directia normalei ![]() , dar sens contrar. Astfel, ecuatia (5.5) devine
, dar sens contrar. Astfel, ecuatia (5.5) devine
![]() (5.10)
(5.10)
Ecuatia (5.10) reprezinta ecuatia macroscopica a miscarii fluidelor perfecte si exprima teorema impulsului, enuntata astfel: variatia in timp a impulsului masei de fluid care ocupa volumul V este egala cu suma dintre forta de greutate si fortele de presiune pe suprafata S care margineste domeniul de control cu volumul V.
|
Figura 5.2. Schema deducerii teoremei impulsului pentru un tub de curent |
In cazul unui tub de curent (figura 5.2), aria suprafetei de control se compune din ariile suprafetelor de intrare A , de iesire A , respectiv laterala Al ale tubului. Indexand cu 1, 2 valorile medii ale marimilor in sectiunile de intrare, respectiv de iesire, ecuatia (5.10) imbraca forma
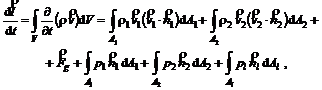
unde al doilea termen din prima egalitate a fost trecut, cu semn schimbat, in a doua egalitate. Stiind ca
![]()
unde ![]() este forta de
presiune pe suprafata laterala a tubului de curent, relatia de
mai sus devine
este forta de
presiune pe suprafata laterala a tubului de curent, relatia de
mai sus devine
![]() (5.11)
(5.11)
Daca miscarea este stationara, membrul stang al ecuatiei (5.11) este nul, iar daca fluidul este incompresibil 1 = 2 = si astfel ecuatia (5.11) se reduce la forma
![]() (5.12)
(5.12)
in care s-a tinut seama de ecuatia continuitatii (4.34)
si s-a inlocuit rezultanta presiunilor suprafetei tubulare asupra
lichidului cu actiunea lichidului asupra suprafetei, potrivit
principiului actiunii si reactiunii, exprimat sub forma ![]() . Forta
. Forta ![]() se numeste
forta de impuls sau reactiunea impulsului.
se numeste
forta de impuls sau reactiunea impulsului.
Ecuatia (5.12) exprima teorema impulsului pentru un tub de curent de fluid incompresibil aflat in miscare stationara. Cu ajutorul ei se pot determina: forta de impact a jeturilor asupra peretilor, forta de impuls a fluidului aflat in miscare asupra unei conducte curbe, pierderea locala de energie provocata de variatia brusca a sectiunii unei conducte etc.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |