Spatiul si timpul in mecanica clasica.
Nu poate fi descrisa starea mecanica a unui corp sau a unui sistem de corpuri, decat daca o racordam la spatiu si timp. In general materia care ne inconjoara este intr-un continuu proces de miscare, iar miscarea ca mod de existenta a materiei se realizeaza in spatiu si timp.
Din punct de vedere al mecanicii clasice atat spatiul cat si timpul au un caracter absolut. Aceasta inseamna ca indiferent de locul nostru in univers, dimensiunile unui anumit obiect si durata unui anumit proces fizic sunt aceleasi. Spatiul este omogen si izotrop, adica proprietatile lui nu se modifica la translatia ori rotatia unui sistem fizic. In ceea ce priveste timpul, acesta este omogen, ceea ce inseamna ca pe axa unidimensionala a timpului duratele de timp se scurg la fel, indiferent de momentele de timp intre care se face masuratoarea, evident respectandu-se cauzalitatea, care cere ca evenimentele sa se produca intr-o succesiune determinata si anume de la trecut spre viitor.
Pentru a descrie miscarea sau repausul este nevoie de un reper spatial si un reper temporal. Reperul spatial este constituit din sistemul de obiecte fizice in raport cu care este specificata pozitia oricarui punct material, sau in general, a oricarui obiect fizic.
Fiecarui reper spatial ii vom asocia, de regula, un sistem de axe de coordonate cu ajutorul carora putem preciza coordonatele spatiale ale obiectului. Reperul temporal este constituit dintr-un "ceasornic", asociat reperului spatial. Prin "ceasornic" intelegem un proces fizic (in general un proces de mare regularitate), ale carui evenimente sunt luate drept reper pentru definirea succesiunii ce caracterizeaza orice alta multime de evenimente.
Ansamblul format din reperul spatial si reperul temporal poarta numele de sistem de referinta sau referential.
Revenind la reperul spatial, deoarece in mecanica clasica spatiul este plat, euclidian si tridimensional, rezulta ca acestui reper trebuie sa i se ataseze trei axe de coordonate, deoarece in virtutea tridimensionalitatii spatiului sunt suficiente trei marimi independente pentru a caracteriza complet pozitia spatiala a unui corp, acestea fiind chiar coordonatele spatiale corespunzatoare.
Cele trei axe de coordonate pot fi linii drepte sau curbe, iar directia si sensul acestora este indicat prin trei vectori unitari, numiti versori. Daca cele trei axe sunt linii drepte, atunci sistemul nostru de coordonate se numeste sistem de coordonate rectiliniu, iar daca cel putin o axa nu este linie dreapta sistemul se numeste sistem de coordonate curbiliniu. Daca cei trei versori atasati axelor sunt mutual perpendiculari, atunci spunem ca avem de-a face cu un sistem de coordonate ortogonale.
Cel mai utilizat sistem de coordonate este sitemul de coordonate carteziene,
care este un sistem de coordonate rectilinii ortogonale.Se poate vedea din
figura 1.1 ca in acest caz
coordonatele unui punct material se obtin prin proiectia
pozitiei acestuia pe cele trei axe de coordonate, coordonatele fiind ![]()
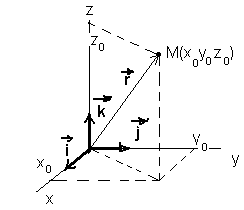
Figura 1.1 Sistemul de coordonate carteziene
Pozitia
punctului material M, daca se tine cont de versorii ![]() poate fi descrisa
si cu ajutorul vectorului de pozitie (sau razei vectoare)
poate fi descrisa
si cu ajutorul vectorului de pozitie (sau razei vectoare) ![]() astfel ;
astfel ;
![]() (1)
(1)
Alte sisteme de coordonate folosite des in fizica mai sunt sistemul de coordonate cilindrice, polare in plan si sferice, acestea fiind ilustrate in figurile 1.2 , 1.3 si 1.4, ele facand parte din clasa sistemelor de coordonate curbilinii ortogonale.
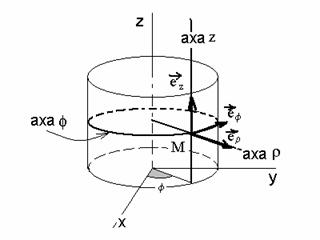
Figura 1.2. Sistemul de coordonate cilindrice ( ![]() )
)
(![]() )
)
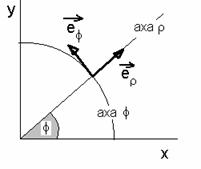
Figura 1.3. Sistemul de coordonate polare in plan
(![]() )
)
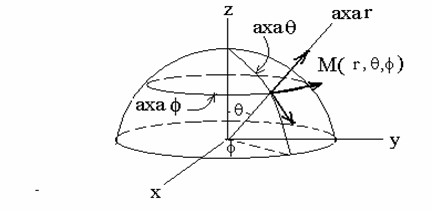
Figura 1.4. Sistemul de coordonate polare sferice
(![]() )
)
Daca mobilul a carui miscare dorim sa o descriem se misca pe traiectorie, astfel ca intr-un timp dt ( timp infinitezimal) ajunge din M in M' atunci raza vectoare a lui M' va fi conform figurii 1.5.
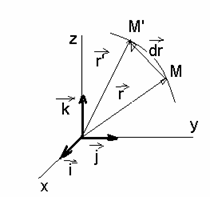
Figura 1.5. Vectorul ![]()
![]() (1.2)
(1.2)
cu
![]() (1.3)
(1.3)
Intr-un alt sistem de coordonate, de exemplu in coordonate curbilinii
ortogonale (fie acestea ![]() ), acelasi vector
), acelasi vector ![]() va putea fi scris
astfel :
va putea fi scris
astfel :
![]() (1.4)
(1.4)
aici ![]() fiind niste
coeficienti care se determina din conditia ca
fiind niste
coeficienti care se determina din conditia ca ![]() sa fie un invariant si care poarta numele de
coeficienti Lamé.
sa fie un invariant si care poarta numele de
coeficienti Lamé.
In mod corespunzator, in coordonate carteziene definim volumul infinitezimal :
![]() (1.5)
(1.5)
sau :
![]() (1.6)
(1.6)
acelasi element exprimat in coordonate curbilinii ortogonale. Putem de asemenea defini elementul de suprafata infinitezimala, de exemplu
![]() (1.7)
(1.7)
sau
![]() (1.8)
(1.8)
in coordonate curbilinii ortogonale.
Sistemele de referinta fata de care studiem miscarea corpurilor se clasifica in referentiale inertiale si referentiale neinertiale. In cazul sistemelor de referinta inertiale, acestea se misca rectiliniu si uniform unele fata de celelalte. Sistemele de referinta neinertiale sunt acelea care nu se misca rectiliniu si uniform unele fata de celelalte.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |