Teorema Poynting in vid fara sarcini
In
absenta sarcinilor (![]() ), teorema Poynting se scrie local:
), teorema Poynting se scrie local:
![]() (31)
(31)
unde ![]() este energia
electromagnetica volumica.
este energia
electromagnetica volumica.
In cazul in care termenul de
productie ![]() este nul, energia electromagnetica
se conserva. Integran pe volumul V se obtine
este nul, energia electromagnetica
se conserva. Integran pe volumul V se obtine
![]() (32)
(32)
Aceasta relatie exprima bilantul intre energia electromagnetica continuta in volumul V:
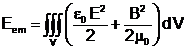
si fluxul energetic (puterea expulzata) spre exterior prin suprafata S ce delimiteaza volumul:
![]()
Deci, in vid si in absenta sarcinilor, o variatie a energiei electromagnetice se traduce printr-o radiatie.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |