Numerele naturale:
(1) 1 este un numar natural;
(2) succesorul unui numar natural este un numar natural.
Structuri de tip arbore:
(1) r este un arbore (numit arbore gol sau arbore cu un singur nod)
(2) daca a1 si a2 sunt arbori, atunci structura
este un arbore ( reprezentat rasturnat). [1.a]
Functia factorial n! (definita pentru intregi pozitivi):
(1)
(2) Daca n > , atunci n! n*(n-1)!
Puterea recursivitatii rezida evident in posibilitatea de a defini un set infinit de obiecte printr-o relatie sau un set de relatii finit, caracteristica evidentiata foarte bine de exemplele furnizate mai sus.
Cunoscuta ca si un concept fundamental in matematica, recursivitatea a devenit si o puternica facilitate de programare odata cu aparitia limbajelor de nivel superior care o implementeaza ca si caracteristica intrinseca (ALGOL, PASCAL, C, JAVA etc.).
In contextul programarii, recursivitatea este strans legata de iteratie si pentru a nu da nastere unor confuzii, se vor defini in continuare cele doua concepte din punctul de vedere al tehnicilor de programare.
Iteratia este executia repetata a unei portiuni de program, pana in momentul in care se indeplineste o conditie respectiv atata timp cat conditia este indeplinita.
Fiecare executie se duce pana la capat, se verifica indeplinirea conditiei si in caz de raspuns nesatisfacator se reia executia de la inceput.
Exemple clasice in acest sens sunt structurile repetitive WHILE, REPEAT si FOR
Recursivitatea presupune de asemenea executia repetata a unei portiuni de program.
In contrast cu iteratia insa, in cadrul recursivitatii, conditia este verificata in cursul executiei programului (nu la sfarsitul ei ca la iteratie) si in caz de rezultat nesatisfacator, intreaga portiune de program este apelata din nou ca subprogram (procedura) a ei insasi, in particular ca procedura a portiunii de program originale care inca nu si-a terminat executia.
In momentul satisfacerii conditiei de revenire, se reia executia programului apelant exact din punctul in care s-a apelat pe el insusi.
Acest lucru este valabil pentru toate apelurile anterioare satisfacerii conditiei.
Utilizarea algoritmilor recursivi este potrivita in situatiile care presupun recursivitate (calcule, functii sau structuri de date definite in termeni recursivi).
In general, un program recursiv P, poate fi exprimat prin multimea P care consta dintr-o serie de instructiuni fundamentale Si (care nu-l contin pe P) si P insusi.
P P [Si,P] [1.b]
Structurile de program necesare si suficiente pentru exprimarea recursivitatii sunt procedurile, subrutinele sau functiile care pot fi apelate prin nume.
Daca o procedura P contine o referinta directa la ea insasi, se spune ca este direct recursiva
Daca P contine o referinta la o alta procedura Q care la randul ei contine o referinta (directa sau indirecta) la P, se spune ca P este recursiva indirect (figura 1.a).
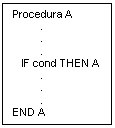
(a)
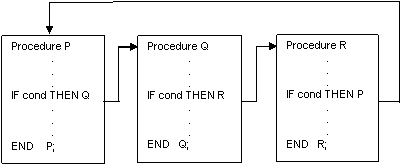
(b)
Fig.1.a. Recursivitate directa (a) si recursivitate indirecta (b)
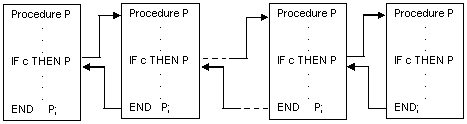
Fig.1.b. Model de executie al unei proceduri recursive
Intuitiv, executia unei proceduri recursive este prezentata in figura 1.b.
Fiecare reprezentare asociata procedurii reprezinta o instanta de apel recursiv a acesteia.
Instantele se apeleaza unele pe altele pana in momentul in care conditia c devine falsa.
In acest moment se revine pe lantul apelurilor in ordine inversa, continuand executia fiecarei instante din punctul de intrerupere pana la sfarsit, dupa cum indica sagetile.
Suprapunand imaginar toate aceste figuri peste una singura, se obtine modelul de executie al unei proceduri recursive.
De regula, unei proceduri i se asociaza un set de obiecte locale procedurii (variabile, constante, tipuri si proceduri) care sunt definite local in procedura si care nu exista sau nu au inteles in afara ei.
Multimea acestor obiecte constituie asa numitul context al procedurii.
De fiecare data cand o astfel de procedura este apelata recursiv, se creeaza un nou set de astfel de variabile locale specifice apelului cu alte cuvinte un nou context specific apelului, care se salveaza in stiva sistem.
Desi aceste variabile au acelasi nume ca si cele corespunzatoare lor din instanta anterioara a procedurii (in calitate de program apelant), ele au valori distincte si orice conflict de nume este evitat prin regula care stabileste domeniul de existenta al identificatorilor.
Regula este urmatoarea: Identificatorii se refera intotdeauna la setul cel mai recent creat de variabile, adica la contextul aflat in varful stivei.
Aceasi regula este valabila si pentru parametrii de apel ai procedurii care sunt asociati prin definitie setului de variabile.
Pe masura ce se realizeaza apeluri recursive, contextul fiecarui apel este salvat in stiva, iar pe masura ce executia unei instante s-a incheiat, se restaureaza contextul instantei apelante prin eliminarea contextului aflat in varful stivei.
Acest mecanism de implementare a recursivitatii este ilustrat in figura 1.c.
PROCEDURE A(x: Tip1; y:Tip2);
BEGIN
END A ;
Fig.1.c. Mecanism pentru implementarea recursivitatii
In legatura cu acest mecanism se pot face cateva observatii:
In cadrul apelurilor recursive nu apar nici un fel de probleme referitoare la transmiterea parametrilor interinstante de apel, daca acesti parametri se transmit prin valoare, ei fiind salvati in stiva odata cu contextul.
2. In cazul parametrilor de tip VAR care se transmit prin adresa, pentru a face posibila transmiterea valorilor acestor parametri intre instantele de apel, este necesara declararea suplimentara a unor parametri locali, cate unul pentru fiecare parametru de tip VAR, care sa asigure retransmiterea valorilor calculate interinstante. Acesti parametri trebuiesc reasignati cu valorile initiale inaintea revenirii din procedura recursiva [1.c].
PROCEDURE A(x: Tip1; VAR y: Tip2; VAR z: Tip3);
VAR u,w: TipX;
y1: Tip2;
z1: Tip3;
BEGIN
[1.c]
A(x,y1,z1);
y:= y1;
z:= z1;
END;
3. In cazul parametrilor de tip referinta trebuie tinut cont de faptul ca in urma apelului recursiv al unei proceduri se realizeaza automat si atribuirea parametrilor implicati in apel [1.d].
PROCEDURE A(r: TipReferinta);
BEGIN [1.d]
A(r^.drept);
END;
Ca si in cazul structurilor repetitive, procedurile recursive necesita evaluarea unei conditii de terminare, fara de care un apel recursiv conduce la o bucla de program infinita.
Astfel, orice apel recursiv al procedurii P trebuie supus controlului unei conditii c care la un moment dat devine neadevarata.
In baza acestei observatii, un algoritm recursiv poate fi exprimat cu mai mare acuratete prin una din formulele [1.e] sau [1.f]:
P s IF c THEN P [Si,P] [1.e]
P s P [Si,IF c THEN P] [1.f]
Tehnica de baza in demonstrarea terminarii unei iteratii (repetitii) consta in:
(1) A defini o functie f(x) (unde x este o variabila din program), astfel incat conditia f(x)< sa implice satisfacerea conditiei de terminare a iteratiei
(2) A demonstra ca f(x) descreste pe parcursul executiei iteratiei respective.
Intr-o maniera similara, terminarea unui algoritm recursiv poate fi demonstrata, dovedind ca P descreste pe f(x)
O modalitate particulara uzuala de a realiza acest lucru, este de a asocia lui P un parametru, spre exemplu n si de a apela recursiv pe P utilizand pe n-1 ca si valoare de parametru.
Daca se inlocuieste conditia c cu n > , se garanteaza terminarea.
Acest lucru se poate exprima formal cu ajutorul urmatoarelor scheme de program [1.g,h]:
P(n) s IF n > 0 THEN P [Si,P(n-1)] [1.g]
P(n) s P [Si,IF n > 0 THEN P(n-1)] [1.h]
De regula in aplicatiile practice trebuie demonstrat nu numai ca adancimea recursivitatii este finita ci si faptul ca ea este suficient de mica.
Motivul este ca fiecare apel recursiv al procedurii P, necesita alocarea unui volum de memorie variabilelor sale curente (contextului procedurii).
In plus, alaturi de aceste variabile trebuie memorata si starea curenta a programului, cu scopul de a fi refacuta, atunci cand apelul curent al lui P se termina si urmeaza sa fie reluata instanta apelanta.
Neglijarea acestor aspecte poate avea drept consecinta depasirea spatiului de memorie alocat stivei sistem, greseala frecventa in contextul utilizarii procedurilor recursive.
Pentru exemplificare se furnizeaza in continuare trei exemple de proceduri recursive simple.
Exemplul 1.1.a. Scopul programului furnizat in continuare ca exemplu, este acela de a ilustra principiul de functionare al unei proceduri recursive.
In cadrul programului se defineste procedura recursiva Revers:
Procedura Revers citeste cate un caracter si il afiseaza.
In acest scop in cadrul procedurii se declara variabila locala z:char.
Procedura verifica daca caracterul citit este blanc:
In caz negativ procedura se autoapeleaza recursiv
In caz afirmativ afiseaza caracterul z [1.1.a].
PROCEDURE Revers;
VAR z: char;
BEGIN [1.1.a]
Read(z);
IF z<>' ' THEN Revers;
Write(z)
END;
Executia procedurii Revers conduce la afisarea caracterelor in ordinea in care sunt citite pana la apritia primului blanc.
Fiecare autoapel presupune salvarea in stiva sistemului a contextului apelului care in situatia de fata consta doar din variabila locala z
Aparitia primului caracter blanc presupune suprimarea apelurilor recursive ale procedurii declansand continuarea executiei procedurii, pana la terminarea sa pentru fiecare din apelurile anterioare.
In cazul de fata, aceasta presupune afisarea caracterului memorat in variabila z
Acest sir de reveniri va produce la inceput afisarea unui blanc, dupa care sunt afisate caracterele in ordinea inversa a citirii lor.
Acest lucru se intampla deoarece fiecare terminare a executiei procedurii determina revenirea in apelul anterior, revenire care presupune reactualizarea contextului apelului.
Intrucat contextele sunt salvate in stiva, reactualizarea lor se face in sens invers ordinii in care au fost memorate.
De fapt pentru fiecare cuvant introdus procedura Revers furnizeaza cuvantul in cauza urmat de acelasi cuvant scris invers.
Exemplul 1.1.b. Se refera la procedura de traversare a unei liste simplu inlantuite [1.1.b].
TYPE TipLista = ^TipNod;
TipNod = RECORD
data: TipData;
urm: TipLista
END;
PROCEDURE Traversare(p:TipLista);
BEGIN
IF p<>nil THEN
BEGIN
Prelucrare(p^.data);
Traversare(p^.urm)
END
END;
Algoritmul de traversare nu numai ca este foarte simplu si foarte elegant, dar prin simpla inversare a instructiunilor Prelucrare si Traversare ([1] respectiv [2]) se obtine parcurgerea in sens invers a listei in cauza.
In acest ultim caz algoritmul se poate descrie astfel.
Se traverseaza mai intai lista incepand cu pozitia curenta pana la sfarsitul listei;
Dupa ce s-a realizat aceasta traversare se prelucreaza informatia din nodul curent;
Consecinta executiei algoritmului:
Informatia continuta intr-o anumita pozitie p este prelucrata numai dupa ce au fost prelucrate toate informatiile corespunzatoare tuturor nodurilor care ii urmeaza lui p
Exemplul 1.1.c. Se refera la binecunoscuta problema a Turnurilor din Hanoi a carei specificare este urmatoarea:
Se considera trei vergele A,B si C;
Se considera de asemenea un set de n discuri gaurite fiecare de alta dimensiune, care sunt amplasate in ordine descrescatoare, de jos in sus pe vergeaua A;
Se cere sa se mute discurile pe vergeaua C utilizand ca si auxiliar vergeaua B;
Se va respecta urmatoarea restrictie:
Nu se aseaza niciodata un disc mai mare peste un disc mai mic (figura 1.1.a).
A B C
Fig.1.1.a. Turnurile din Hanoi
Problema pare simpla, dar rezolvarea ei cere multa, rabdare, acuratete si un volum de timp care creste exponential odata cu n.
O abordare recursiva insa reprezinta o solutie simpla si eleganta.
Rezolvarea recursiva a problemei presupune abordarea unui caz simplu, urmata de generalizarea corespunzatoare.
Astfel pentru inceput se considera ca exista doar doua discuri numerotate cu 1 (cel mai mic situat deasupra) respectiv cu 2 (cel mai mare), a caror mutare in conditiile impuse presupune urmatorii pasi :
Se muta discul 1 de pe A pe B;
Se muta discul 2 de pe A pe C;
Se muta discul 1 de pe B pe C.
Prin generalizare se reia acelasi algoritm pentru n discuri (figura 1.1.b), adica:
Se muta n-1 discuri (cele de deasupra) de pe A pe B (prin C);
Se muta discul n de pe A pe C;
Se muta n-1 discuri de pe B pe C (prin A).
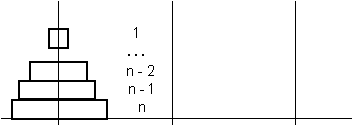
A B C
Fig.1.1.b. Generalizarea problemei Turnurilor din Hanoi
Pornind de la acest model, o varianta imediata de implementare recursiva a rezolvarii problemei este prezentata in secventa [1.1.a].
PROCEDURE TurnuriHanoi(NrDiscuri:integer; A,
B, C: TipVergele);
PROCEDURE MutaDisc(x,y: TipVergele);
BEGIN
* muta discul de la x la y
END;
BEGIN
IF NrDiscuri=1 THEN
MutaDisc(A,C) [1.1.a]
ELSE
BEGIN
TurnuriHanoi(NrDiscuri-1, A, B, C);
MutaDisc(A,C);
TurnuriHanoi(NrDiscuri-1, B, C, A)
END
END;
Procedura MutaDisc realizeaza efectiv mutarea unui disc de pe o vergea sursa pe o vergea destinatie.
Procedura TurnuriHanoi realizeaza doua auto-apeluri recursive si un apel al procedurii MutaDisc conform modelului de generalizare prezentat mai sus.
Algoritmii recursivi sunt potriviti a fi utilizati atunci cand problema care trebuie rezolvata sau datele care trebuiesc prelucrate sunt definite in termeni recursivi.
Cu toate acestea, un astfel de mod de definire nu justifica intotdeauna faptul ca utilizarea unui algoritm recursiv reprezinta cea mai buna alegere.
Mai mult, utilizarea recursivitatii in anumite situatii nepotrivite, coroborata cu regia relativ ridicata a implementarii si executiei unor astfel de algoritmi, a generat in timp un curent de opinie potrivnic destul de vehement.
Cu toate acestea recursivitatea ramane o tehnica de programare fundamentala cu un domeniu de aplicabilitate bine delimitat.
Programele in care utilizarea recursivitatii este recomandata se incadreaza in modelul [1.e,f].
Acest model este foarte potrivit in cazurile in care se cere calculul unor valori care se definesc cu ajutorul unor relatii recurente.
Un exemplu clasic in acest sens il reprezinta numerele factoriale fi=i! precizate in [2.1.a]
i = 0,1,2,3,4,5,
fi=1,1,2,6,24,120, [2.1.a]
Elementul cu indicele 0 este furnizat in mod explicit ca fiind egal cu 1.
Elementele urmatoare, sunt definite in mod recursiv, in termenii predecesorilor lor [2.1.b].
fi+1=(i+1)*fi [2.1.b]
Pornind de la aceasta formula, se introduc doua variabile i si f care precizeaza respectiv valorile lui i si fi , in cel de-al i-lea nivel de recursivitate [2.1.c].
i:= i+1; f:= i*f; [2.1.c]
Inlocuind [2.1.c] in [1.e] se obtine forma recursiva [2.1.d] careia i se poate asocia programul principal [2.1.e].
P s IF i<n THEN (i:= i+1; f:= i*f; P [2.1.d]
i:= 0; f:= 1; P; [2.1.e]
Varianta imediata de implementare a procedurii P apare in secventa [2.1.f].
PROCEDURE P;
BEGIN
IF i<n THEN
BEGIN [2.1.f]
i:= i+1; f:= i*f; P
END
END;
Dupa cum s-a precizat, algoritmii recursivi se recomanda a fi utilizati cu precadere pentru implementarea unor probleme care se pot defini in maniera recursiva.
Cu toate acestea, recursivitatea poate fi utilizata si in cazul unor probleme de natura nerecursiva.
Spre exemplu, in [2.1.g] se prezinta un exemplu de implementare recursiva a unei cautari intr-un tablou liniar a
VAR n: integer; x: TipElement;
a: ARRAY[1..n] OF TipElement;
FUNCTION Cauta(i: TipIndice): TipIndice;
BEGIN
IF i>n THEN Cauta:= 0 ELSE [2.1.g]
IF a[i]=x THEN Cauta:= i ELSE
Cauta:= Cauta(i+1)
END;
Este evident faptul ca o astfel de abordare este posibila, dar ea este oarecum fortata si ineficienta, varianta iterativa fiind preferata in acest caz.
Procedura P prezentata in paragraful anterior este de regula inlocuita cu un subprogram de tip functie,
Functia poate fi utilizata direct ca si constituent al unei expresii
Functiei i se poate asocia in mod explicit valoarea rezultata din calcule.
Variabila f devine superflua, iar rolului lui i este preluat de catre parametrul n de apel al functiei [2.2.a].
FUNCTION Fact(n: integer): integer;
BEGIN
IF n=0 THEN
Fact:= 1 [2.2.a]
ELSE
Fact:= n*Fact(n‑1)
END;
Secventa in cauza care a fost redactata pentru calculul factorialului ca si intreg, este limitata din punctul de vedere al dimensiunii maxime a lui n din ratiuni de reprezentare in calculator a numerelor intregi.
Trecerea la varianta reala, eliberata de aceasta constrangere este extrem de simpla.
In figura 2.2.a apare reprezentarea intuitiva a apelurilor recursive ale functiei Fact pentru n = 4
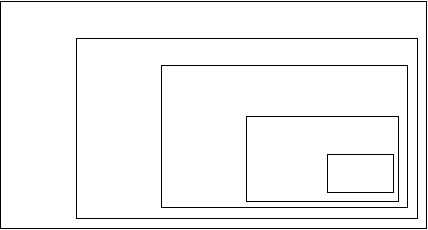
Fact(4)
Fact(3)
Fact(2)
Fact(1)
Fact(0)
=4* =3* =2* =1* =1
Fig.2.2.a. Apelurile ale functiei recursive Fact pentru n = 4
In figura 2.2.b, se prezinta intuitiv revenirile succesive din apelurile
recursive ale functiei Fact, care au drept urmare calculul efectiv al valorii
factorialului.
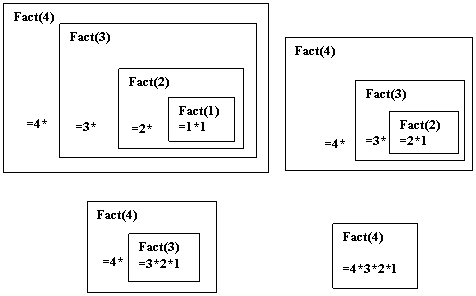
Fig.2.2.b. Rezolvarea apelurilor functiei recursive Fact pentru n = 4
In figura 2.2.c apare structura apelurilor respectiv a rezolvarii acestora in forma de arbore de apeluri.
Apeluri: Reveniri:
4! 4! 4! 4! 4! 24
4 * 3! 4 * 3! 4 * 3! 4 * 3! 4 * 6
3 * 2! 3 * 2! 3 * 2! 3 * 2
2 * 1! 2 * 1! 2 * 1
1 * 0! 1 * 1
1
Fig.2.2.c. Arborele de apeluri al functiei Fact(4)
In acest caz fiind vorba despre despre o functie cu un singur apel recursiv, arborele de apeluri are o structura de lista liniara.
Fiecare apel adauga un element la sfarsitul acestei liste, iar rezolvarea apelurilor are drept consecinta reducerea succesiva a listei de la sfarsit spre inceput.
Dupa cum se observa, pentru a calcula factorialul de ordinul n sunt necesare n+1 apeluri ale functiei recursive Fact
Este insa evident ca in cazul calculului factorialului, recursivitatea poate fi inlocuita printr-o simpla iteratie [2.2.b].
VAR i,fact: integer;
i:= 0; fact:= 1;
WHILE i<n DO [2.2.b]
BEGIN
i:= i+1; fact:= fact*i
END;
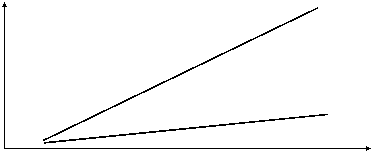
In figura 2.2.d. apre reprezentarea grafica a profilului performantei algoritmului de calcul al factorialului in varianta recursiva respectiv iterativa.
Sunt de fapt reprezentati in maniera comparativa, timpii de executie pe un acelasi sistem de calcul, ai celor doi algoritmi functie de valoarea lui n
Dupa cum se observa, desi ambii algoritmi sunt liniari in raport cu n, adica au performanta O(n) , algoritmul recursiv este de aproximativ 4 ori mai lent decat cel iterativ.
Expresiile analitice ale celor doua reprezentari apar in [2.2.c][De84].
Timp [sec]
0.9 recursiv
iterativ
20 40 60 80 100 120 n
Fig.2.2.d. Profilul algoritmului factorial (variantele recursiva si iterativa)
Ti(n)=0.0018*n+0.0033 [2.2.c]
Tr(n)=0.0056*n+0.017
Exista si alte exemple de definiri recursive care se trateaza mult mai eficient cu ajutorul iteratiei.
Un exemplu in acest sens il reprezinta calculul numerelor lui Fibonacci de ordin 1 care sunt definite prin urmatoarea relatie recursiva [2.3.a]:
Fibn+1 = Fibn + Fibn-1 pentru n > 0
Fib1 = 1; Fib0 = 0 [2.3.a]
Aceasta definitie recursiva conduce imediat la urmatorul algoritm de calcul recursiv [2.3.b].
FUNCTION Fib(n: integer): integer;
BEGIN
IF n=0 THEN Fib:= 0 ELSE [2.3.b]
IF n=1 THEN Fib:= 1 ELSE
Fib:= Fib(n‑1) + Fib(n‑2)
END;
Din pacate modelul recursiv utilizat in aceasta situatie conduce la o maniera ineficienta de calcul, deoarece numarul de apeluri creste exponential cu n
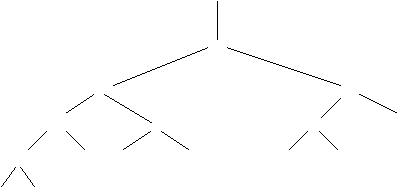
In figura 2.3.a. apare reprezentarea arborelui de apeluri pentru n=
5
4 3
2 2 1
2 1 1 0 1 0
1 0
Fig.2.3.a. Arborele de apeluri al procedurii Fib pentru n = 5
Dupa cum se observa:
Este vorba despre un arbore binar (exista doua apeluri recursive ale procedurii Fib
Parcurgerea arborelui de apeluri necesita 15 apeluri, fiecare nod semnificand un apel al procedurii.
Ineficienta acestei implementari creste odata cu cresterea lui n
Este evident faptul ca numerele lui Fibonacci pot fi calculate cu ajutorul unei scheme iterative care elimina recalcularea valorilor, utilizand doua variabile auxiliare x Fibi si y = Fibi-1 [2.3.c].
i:= 1; x:= 1; y:= 0;
WHILE i<n DO [2.3.c]
BEGIN
z:= x; i:= i+1;
x:= x+y; y:= z
END;
Variabila auxiliara z poate fi evitata, utilizand atribuiri de forma x:= x y si y:= x- y
Recursivitatea reprezinta o facilitate excelenta de programare care contribuie la exprimarea simpla, concisa si eleganta a algoritmilor de natura recursiva.
o Cu toate acestea, ori de cate ori problemele eficientei si performantei se pun cu preponderenta, se recomanda evitarea utilizarii recursivitatii.
o De asemenea se recomanda evitarea recursivitatii ori de cate ori sta la dispozitie o rezolvare evidenta bazata pe iteratie.
De fapt, implementarea recursivitatii pe echipamente nerecursive dovedeste faptul ca orice algoritm recursiv poate fi transformat intr-unul iterativ.
In continuare se abordeaza teoretic problema conversiei unui algoritm recursiv intr-unul iterativ.
In abordarea acestei chestiuni se disting doua cazuri:
Cazul in care apelul recursiv al procedurii apare la sfarsitul ei, drept ultima instructiune a procedurii ('tail recursion').
o In aceasta situatie, recursivitatea poate fi inlocuita cu o bucla simpla de iteratie.
o Acest lucru este posibil, deoarece in acest caz, revenirea dintr-un apel incuibat presupune si terminarea instantei respective a procedurii, motiv pentru care contextul apelului nu mai trebuie restaurat.
Astfel daca o procedura P(x) contine ca si ultim pas al sau un apel la ea insasi de forma P(y)
o Acest apel poate fi inlocuit cu o instructiune de atribuire x:=y , urmata de reluarea (salt la inceputul) codului lui P
o y poate fi chiar o expresie,
o x insa in mod obligatoriu trebuie sa fie o variabila transmisibila prin valoare, astfel incat valoarea ei sa fie memorata intr-o locatie specifica apelului.
o De asemenea x poate fi transmis prin referinta daca y este chiar x
o Daca P are mai multi parametri, ei pot fi tratati fiecare in parte ca x si y
Aceasta modificare este valabila deoarece reluarea executiei lui P, cu noua valoare a lui x , are exact acelasi efect ca si cand s-ar apela P(y) si s-ar reveni din acest apel.
In general programele recursive pot fi convertite formal in forme iterative dupa cum urmeaza.
Forma recursiva [2.4.a] devine forma iterativa [2.4.b] iar [2.4.c] devine [2.4.d].
P(x) s P [Si,IF c THEN P(y)] [2.4.a]
P(x) s P [Si,IF c THEN [x:=y; reluare P]] [2.4.b]
P(n) s P [Si,IF n>0 THEN P(n-1)] [2.4.c]
-------- ----- ------ ----- ----- -----------------
P(n) s P [Si,IF n>0 THEN [n:=n-1; reluare P]] [2.4.d]
-------- ----- ------ ----- ----- -----------------
Exemple concludente in acest sens sunt implementarea iterativa a calculului factorialului si a calculului sirului numerelor lui Fibonacci prezentate anterior.
Cazul in care apelul sau apelurile recursive se realizeaza din interiorul procedurii [2.4.e].
o Varianta iterativa a acestei situatii presupune tratarea explicita de catre programator a stivei apelurilor.
o Fiecare apel necesita salvarea in stiva gestionata de catre utilizator a contextului instantei de apel,
o Acest context trebuie restaurat de catre utilizaator din aceeasi stiva la terminarea instantei.
P s P [Si, IF c THEN P, Sj] [2.4.e]
Activitatea de conversie in acest caz are un inalt grad de specificitate functie de algoritmul recursiv care se doreste a fi convertit si este in general dificila, laborioasa si ingreuneaza mult intelegerea algoritmului.
Un exemplu in acest sens il reprezinta partitionarea nerecursiva prezentata in paragraful &3.2.6.
Recursivitatea are insa domeniile ei bine definite in care se aplica cu succes.
In general se apreciaza ca algoritmii a caror natura este recursiva este indicat a fi formulati ca si proceduri recursive, lucru pus in evidenta de algoritmii prezentati in cadrul acestui capitol si in capitolele urmatoare.
Daca unul dintre numere este nul, c.m.m.d.c. al lor este celalalt numar;
Daca nici unul din numere nu este nul, atunci c.m.m.d.c nu se modifica daca se inlocuieste unul din numere cu restul impartirii sale cu celalalt.
Pornind de la aceasta definitie recursiva se poate concepe un subprogram simplu de tip functie pentru calculul c.m.m.d.c. a doua numere intregi [3.1.a].
FUNCTION Cmmdc(m,n: integer): integer;
BEGIN
IF n=0 THEN
Cmmdc:= m [3.1.a]
ELSE
Cmmdc:= Cmmdc(n, m MOD n)
END;
In figura 3.1.a apare urma executiei acestui algoritm pentru valorile 18 si 27.
|
M |
N |
Cmmdc(n, m MOD n) |
|
Cmmdc(27, 18 mod 27) |
||
|
Cmmdc(18, 27 mod 18) |
||
|
Cmmdc (9, 18 mod 9) |
||
|
n = 0 ; Cmmdc = 9 |
Fig.3.1.a. Urma executiei algoritmului lui Euclid
Exemplul 2. Algoritm pentru transformarea expresiilor aritmetice specificate in format infix in format postfix (notatie poloneza).
o Expresiile aritmetice uzuale (format infix) se definesc in mod recursiv cu ajutorul diagramelor sintactice prezentate in figura 3.1.b.
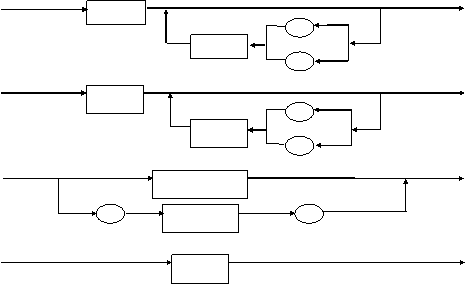Expresie
Termen
+
Termen
-
Termen
Factor
*
Factor
/
Factor
Identificator
( Expresie )
Identificator
litera
Fig.3.1.b. Definirea recursiva a unei expresii aritmetice
o Recursivitatea de natura indirecta a acestei definitii consta in faptul ca definitia lui Factor se refera din nou la definitia lui Expresie
o Se pune problema ca pornind de la o expresie aritmetica corecta furnizata in format normal (infix) sa se obtina forma poloneza (postfix) a acesteia.
o Se precizeaza ca notatia poloneza presupune reprezentarea unei operatii aritmetice simple in forma 'operand operand operator' si nu in forma 'operand operator operand' presupusa de notatia infix.
o Spre exemplu a+b devine ab+ iar a+b*(c-d) devine abcd-*+
o Avantajul notatiei poloneze este acela ca indica ordinea corecta a executiei operatiilor fara a utiliza paranteze, iar expresia poate fi evaluata printr-o simpla baleere secventiala.
Problema care trebuie rezolvata este aceea de a depista cei doi operanzi (care pot fi complecsi), de a-i inregistra si de a trece operatorul dupa ei.
o Din acest motiv, pana la depistarea celui de-al doilea operand, operatorul aditiv din cadrul expresiei respectiv operatorul multiplicativ din cadrul unui termen, se memoreaza in variabilele locale op respectiv op1
o Transformarea ceruta se poate realiza construind cate o procedura individuala de conversie pentru fiecare constructie sintactica (Expresie, Termen, Factor
o Deoarece fiecare dintre aceste constructii sintactice este definita recursiv, procedurile corespunzatoare trebuiesc de asemenea activate recursiv.
o Algoritmul de transformare apare in secventa [3.1.b].
TYPE linie = string[80];
VAR infix,post: linie;
c: char;
i: integer;
j: integer;
PROCEDURE CitesteCar(ex: linie; VAR ch: char);
BEGIN
REPEAT
ch:= ex[i]; i:= i+1;
UNTIL ch<>' '
END;
PROCEDURE ScrieCar(VAR ex: linie, ch: char);
BEGIN
ex[j]:= ch; j:= j+1
END; [3.1.b]
PROCEDURE Expresie;
VAR op: char;
PROCEDURE Termen;
VAR op1: char;
PROCEDURE Factor
BEGIN
IF c ='(' THEN
BEGIN
CitesteCar(infix,c); expresie
END
ELSE
BEGIN
ScrieCar(post,c)
END;
CitesteCar(infix,c);
END;
BEGIN
Factor;
WHILE (c ='*') OR (c ='/') DO
BEGIN
op1:= c; CitesteCar(infix,c);
Factor;
ScrieCar(post,op1)
END
END;
BEGIN
Termen;
WHILE (c ='+') OR (c ='-') DO
BEGIN
op:= c; CitesteCar(infix,c);
Termen;
ScrieCar(post,op)
END
END;
In cadrul algoritmului se definesc:
o Procedurile Expresie, Termen si Factor conform diagramelor din fig. 3.1.b
o Variabile locale op si op1 utilizate pentru memorarea operatorilor aditivi respectiv multiplicativi.
o Procedura CitesteCar care furnizeaza caracterul urmator din textul de analizat eliminand eventualele blancuri.
o Variabila ch care in fiecare moment memoreaza caracterul furnizat de procedura CitesteCar
o Se considera ca expresia in format infix ce urmeaza a fi convertita este depusa ca sir de caractere in tabloul infix parcurs cu ajutorul indicelui i
o Forma postfix a expresiei se asambleaza in tabloul post utilizand in acest scop indicele j
o Indicii i si j trebuiesc intializati in programul principal care apeleaza procedura Expresie
o Pentru functionarea corecta a procedurii de conversie, expresia de procesat trebuie precizata intre paranteze.
Una dintre metodele fundamentale de proiectare a algoritmilor se bazeaza pe tehnica divizarii ('devide and conquer').
Principiul de baza al acestei tehnici este acela de a descompune (divide) o problema complexa in mai multe subprobleme a caror rezolvare este mai simpla si din solutiile carora se poate asambla simplu solutia problemei initiale.
Acest mod de lucru se repeta recursiv pana cand subproblemele devin banale iar solutiile lor evidente.
O aplicatie tipica a tehnicii divizarii are structura recursiva prezentata in [3.2.a].
PROCEDURE Rezolva(x);
BEGIN
IF *x este divizibil in subprobleme THEN
BEGIN [3.2.a]
*divide pe x in doua sau mai multe parti:
x1,x2,..,xk;
Rezolva(x1); Rezolva(x2),; Rezolva(xk);
*combina cele k solutii partiale intr‑o
solutie pentru x
END
ELSE
*rezolva pe x direct
END;
Daca recombinarea solutiilor partiale este substantial mai simpla decat rezolvarea intregii probleme, aceasta tehnica conduce la proiectarea unor algoritmi intr-adevar eficienti.
Datorita celor k apeluri recursive, arborele de apeluri asociat procedurii Rezolva este de ordinul k
Analiza algoritmilor de divizare
o Se presupune ca timpul de executie al rezolvarii problemei de dimensiune n este T(n)
o In conditiile in care prin divizari succesive problema de rezolvat devine suficient de redusa ca dimensiune, se poate considera ca pentru n c c constant), determinarea solutiei necesita un timp de executie constant, adica Q
o Se noteaza cu D(n) timpul necesar divizarii problemei in subprobleme si cu C(n) timpul necesar combinarii solutiilor partiale.
o Daca problema initiala se divide in k subprobleme, fiecare dintre ele de dimensiune 1/b din dimensiunea problemei originale, se obtine urmatoarea formula recurenta [3.2.b].
Q daca n c
T(n) = [3.2.b]
k T(n/b) D(n) C(n) pentru n > c
In continuare se prezinta cateva aplicatii ale acestei tehnici.
Exemplul 3.2.a
o Un prim exemplu de algoritm de divizare il constituie metoda de sortare Quicksort (&.3.2.6).
o In acest caz problema se divide de fiecare data in doua subprobleme, rezultand un arbore binar de apeluri.
o Combinarea solutiilor partiale nu este necesara deoarece scopul este atins prin modificarile care se realizeaza chiar de catre rezolvarile partiale.
Exemplul 3.2.b. Algoritm pentru determinarea extremelor valorilor componentelor unui vector.
o In acest scop, poate fi proiectata o procedura Domeniu(a,i,j,mic,mare) care atribuie parametrilor mic si mare elementul minim respectiv maxim al vectorului a din domeniul delimitat de indicii i si j a[i]..a[j])
o O implementare iterativa evidenta a procedurii apare in secventa [3.2.c] sub denumirea de DomeniuIt
PROCEDURE DomeniuIt(a: TipTablou; i,j: integer;
VAR mic,mare: integer);
VAR k:integer;
BEGIN
mic:= a[i]; mare:= a[i];
FOR k:=i+1 TO j DO [3.2.c]
BEGIN
IF a[k]>mare THEN mare:= a[k];
IF a[k]<mic THEN mic:= a[k]
END
END;
Procedura baleeaza intregul vector comparand fiecare element cu cel mai mare respectiv cel mai mic element pana la momentul curent.
Este usor de vazut ca costul procedurii Domeniu in termenii numarului de comparatii dintre elementele tabloului este 2*n-2 pentru un vector cu n elemente.
Este de asemenea de observat faptul ca fiecare element al lui a se va compara de doua ori; odata pentru aflarea maximului, iar a doua oara pentru aflarea minimului.
Acest algoritm nu tine cont de faptul ca orice element luat in considerare drept candidat pentru minim (care apare in succesiunea de valori a lui mic) nu poate fi niciodata candidat pentru maxim, exceptand conditia de initializare si reciproc.
Astfel algoritmul risipeste un efort considerabil examinand fiecare element de doua ori. Aceasta risipa se poate evita.
o Aplicand tehnica divizarii, se imparte tabloul in doua parti
o Se compara valorile minime si maxime ale subtablourilor rezultate, stabilindu-se minimul si maximul absolut.
o In continuare se procedeaza in aceeasi maniera reducand de fiecare data la jumatate dimensiunea subtablourilor.
o Pentru dimensiuni 1 sau 2 ale subtablourilor solutia este evidenta.
o O ilustrare a acestei tehnici apare in procedura recursiva Domeniu [3.2.d].
CONST n = ;
TYPE TipTablou = ARRAY[1..n] OF integer;
VAR a: TipTablou;
PROCEDURE Domeniu(a: TipTablou; i,j: integer;
VAR
mic,mare: integer);
VAR mijloc,mic1,mare1,mic2,mare2: integer;
BEGIN
IF j<=i+1 THEN
BEGIN
IF a[i]<a[j] THEN
BEGIN
mic:= a[i]; mare:= a[j]
END
ELSE
BEGIN [3.2.d]
mic:= a[j]; mare:= a[i]
END
END
ELSE
BEGIN
mijloc:= (i+j) DIV 2;
Domeniu(a,i,mijloc,mic1,mare1);
Domeniu(a,mijloc+1,j,mic2,mare2);
IF mare1>mare2 THEN mare:= mare1 ELSE
mare:= mare2;
IF mic1<mic2 THEN mic:= mic1 ELSE mic:= mic2
END
END;
i mijloc mijloc + 1 j
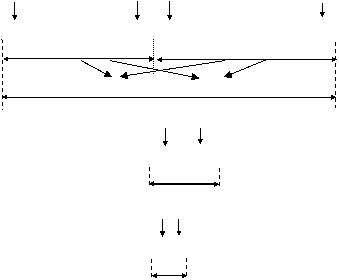
mic1, mare1 mic2, mare2
mic mare
i j (j=i+1)
2
i j (j<i+1)
1
Fig.3.2.a. Functionarea de principiu a procedurii Domeniu.
Se constata analogia evidenta cu structura de principiu prezentata in secventa [3.2.a].
In figura 3.2.a. apare reprezentarea grafica a modului de lucru al procedurii Domeniu
Urma executiei procedurii pentru n = 10 apare in figura 3.2.b,
o In figura apar precizate limitele domeniilor pentru fiecare dintre apelurile procedurii.
o In chenar sunt precizate domeniile de lungime 1 sau 2 care presupun comparatii directe.
o Dupa cum se observa, arborele de apeluri este un arbore binar deoarece se executa doua apeluri recursive din corpul procedurii.
Daca se realizeaza o analiza mai aprofundata a modului de implementare se constata ca:
o Contextele apelurilor se salveaza in stiva sistem in ordinea rezultata de parcurgerea in preordine a arborelui de apeluri
o Contextele se extrag din stiva conform parcurgerii in postordine a acestuia.
o Restaurarea contextului fiecarui apel face posibila parcurgerea ordonata a tuturor posibilitatilor evidentiate de arborele de apeluri.
(1,10)
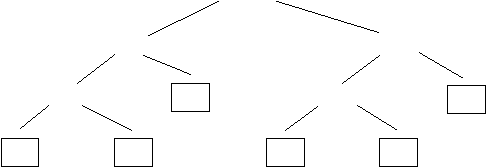
(1,5) (6,10)
(1,3) 4,5 (6,8) 9,10
1,2 3,3 6,7 8,8
Fig.3.2.b. Arbore de apeluri al procedurii Domeniu pentru n = 10
Per ansamblu regia unui astfel de algoritm recursiv este mai ridicata decat a celui iterativ (sunt necesare 11 apeluri ale procedurii, pentru n = 10
Totusi, autorii demonstreaza ca din punctul de vedere al costului calculat relativ la numarul de comparatii ale elementelor tabloului, el este mai eficient decat algoritmul iterativ.
o Pornind de la observatia ca procedura include comparatii directe numai pentru subtablourile scurte (de lungime 1 sau 2)
o Si ca pentru cele mai lungi ea procedeaza la divizarea intervalului comparand numai extremele acestora,
o In [AH85] se indica o valoare aproximativa pentru cost (numar de comparatii directe) egala cu (3/2)n-2 unde n este dimensiunea tabloului analizat.
Analiza algoritmului Domeniu se poate realiza prin particularizarea relatiei [3.2.b].
Se observa imediat ca k = 2, b = 2, iar D(n) si C(n) sunt ambele Q
In consecinta rezulta ecuatia [3.2.e] a carei solutie apare in [2.3.f].
Q(1) daca n
T(n) = [3.2.e]
2 T(n/2) + 2 daca n > 2
Q(T(n))= O(n) [3.2.f]
O alta categorie de algoritmi care se preteaza pentru o abordare recursiva o reprezinta algoritmii de reducere.
o Acesti algoritmi se bazeaza pe reducerea gradului de dificultate al problemei, pas cu pas, pana in momentul in care aceasta devine banala.
o In continuare se revine in maniera recursiva si se asambleaza solutia integrala.
In aceasta categorie pot fi incadrati algoritmul pentru calculul factorialului si algoritmul pentru rezolvarea problemei Turnurilor din Hanoi.
Se atrage atentia ca spre deosebire de algoritmii cu revenire (&4), in acest caz nu se pune problema revenirii in caz de nereusita, element care incadreaza acest tip de algoritmi intr-o categorie separata.
In continuare se prezinta un exemplu de algoritm de reducere.
Exemplul 3.3.a. Algoritm pentru determinarea permutarilor primelor n numere naturale.
o Se da o secventa de numere naturale,
o Pentru determinarea permutarilor se poate utiliza tehnica reducerii.
o Principiul este urmatorul:
Pentru a obtine permutarile de n elemente este suficient sa se fixeze pe rand cate un element si sa se permute toate celelalte n -1 elemente.
Procedand recursiv in aceasta maniera se ajunge la permutari de 1 element care sunt banale.
Aceasta tehnica este implementata de procedura Permut(k) care realizeaza permutarea primelor k numere naturale.
o Numerele se presupun memorate in tabloul a[i](i=1,2,,n)
o Daca k , atunci fiecare dintre elementele tabloului situate pe pozitii inferioare lui k sunt aduse (fixate) pe pozitia k prin interschimbarea pozitiilor i si k ale tabloului a in cadrul unei bucle FOR pentru i=1,2,,k
o Initial k ia valoarea n pentru permutarea a n numere.
o Pentru fiecare schimbare (fixare) se apeleaza recursiv rutina cu parametrul k-1, dupa care se reface starea initiala reluand in sens invers interschimbarea pozitiilor i si k
o Acest lucru este necesar, deoarece fixarea elementului urmator presupune refacerea starii initiale in vederea parcurgerii in mod ordonat, pentru fiecare element in parte a tuturor posibilitatilor.
o In momentul in care k = 1, se considera terminat un apel si se afiseaza tabloul a care contine o permutare.
o Aceasta este conditia care limiteaza adancimea apelurilor recursive determinand revenirea in apelurile anterioare.
Schita de principiu a acestui algoritm apare in [3.3.a.] iar o varianta de rafinare Pascal apare in [3.3.b].
Procedura Permuta(k:integer);
daca k=1 atunci
*afiseaza tabloul (s-a
finalizat o permutare)
altfel
pentru i=1 la k executa [3.3.a]
*interschimba pe a[i] cu a[k];
Permuta(k-1);
*interschimba pe a[i] cu a[k]
PROCEDURE Permuta(k: integer);
VAR i,x: integer;
BEGIN
IF k=1 THEN afiseaza ELSE
BEGIN
FOR i:=1 TO k DO
BEGIN [3.3.b]
x:= a[i]; a[i]:= a[k]; a[k]:= x;
Permuta(k-1);
x:= a[i]; a[i]:= a[k]; a[k]:= x
END
END
END;
In figura 3.3.a este reprezentat arborele de apeluri al procedurii Permuta(4) pentru permutarile obtinute prin fixarea primului element
1 2 3 4
i=1 k=4 i=2 k=4 i=3 k=4 i=4 k=4
4 2 3 1 1 4 3 2 1 2 4 3 1 2 3 4
.
i=1 k=3 i=2 k=3 i=3 k=3
3 2 4 1 4 3 2 1 4 2 3 1
i=1 k=2 i=2 k=2 i=1 k=2 i=2 k=2 i=1 k=2 i=2 k=2
2 3 4 1 3 2 4 1 3 4 2 1 4 3 2 1 2 4 3 1 4 2 3 1
k=1 k=1 k=1 k=1 k=1 k=1
2 3 4 1 3 2 4 1 3 4 2 1 4 3 2 1 2 4 3 1 4 2 3 1
Fig.3.3.a. Arborele de apeluri pentru Permuta(4)
Structura arborelui apelurilor este mai complicata datorita faptului ca apelurile recursive se realizeaza dintr-o bucla FOR cu o limita (k) care descreste odata cu cresterea nivelului arborelui.
Inaltimea arborelui de apeluri este egala cu n
Algoritmii recursivi au proprietatea de a putea evidentia in mod ordonat toate posibilitatile referitoare la o situatie data.
Se prezinta in acest sens doua exemple
o Primul exemplu reliefeaza proprietatea (exemplul 3.4.a).
o Cel de-al doilea exemplu selecteaza din multimea acestor posibilitati, cele care prezinta interes (exemplul 3.4.b).
Exemplul 3.4.a. Algoritm pentru evidentierea tuturor posibilitatilor de sectionare a unui fir de lungime intreaga data (n) in parti de lungime 1 sau 2.
Acest algoritm se bazeaza pe urmatoarea tehnica de lucru:
pentru lungimea n > 1 exista doua posibilitati:
T se taie o parte de lungime 1 si restul lungimii (n-1) se sectioneaza in toate modurile posibile;
T se taie o parte de lungime 2 si restul lungimii (n-2)se sectioneaza in toate modurile posibile.
pentru n = 1 avem cazul banal al unei taieturi de lungime 1.
pentru n = 0 nu exista nici o posibilitate de taietura.
Schita de principiu a acestui algoritm apare in secventa [3.4.a].
Procedura Taie(lungimeFir);
daca lungimeFir>1 atunci
*se taie o bucata de lungime 1;
Taie(lungimeFir-1);
*se taie o bucata de lungime 2;
Taie(lungimeFir-2)
*se anuleaza taietura
altfel [3.4.a]
daca lungimeFir=1 atunci
*se taie bucata de lungime 1;
*afisare
In secventa [3.4.b] se prezinta o varianta de implementare Pascal
Procedura Taie implementeaza tehnica de lucru anterior prezentata cu precizarea ca la atingerea dimensiunii n = 1 sau n = 0 se considera procedura terminata si se afiseaza secventa de taieturi generata.
Taieturile sunt reprezentate grafic utilizand caracterul '.' pentru segmentul de lungime 1 si caracterul '_' pentru segmentul de lungime 2.
Pentru memorarea taieturilor se utilizeaza un tablou de caractere z, parcurs cu ajutorul indicelui k, in care se depun caracterele corespunzatoare taieturilor.
VAR i,k,x: integer;
z: ARRAY[1..9] OF char;
PROCEDURE Taie(lungimeFir: integer);
BEGIN
IF lungimeFir>1 THEN
BEGIN
k:= k+1;
z[k]:= '.';
Taie(lungimeFir-1);
z[k]:= '_';
Taie(lungimeFir-2);
k:= k-1
END
ELSE
BEGIN [3.4.b]
Write(' ');
FOR i:= 1 TO k DO Write(z[i]);
IF lungimeFir=1 THEN Write('.');
Writeln
END
END;
In figura 3.4.a apare rezultatul apelului procedurii Taie pentru n = 4 si n =
Din aceasta figura se poate deduce usor maniera de executie a procedurii (urma executiei) luand in considerare faptul ca in reprezentarea grafica:
Caracterul '.' reprezinta apelul procedurii Taie pentru n-1
Cracterul '_' reprezinta apelul procedurii pentru n - 2
lungimeFir = 4 lungimeFir = 5
. ..
.._ _
._. .._.
_.. ._..
_ _ ._ _
_
_._
_ _.
Fig.3.4.a. Executia procedurii Taie pentru n = 4 si n = 5
In figura3.4.b se prezinta arborele de apeluri al procedurii Taie pentru n = 4
Se observa ca in fiecare nod al acestui arbore sunt precizate:
Succesiunea bucatilor taiate;
Apelul recursiv care se realizeaza;
Valoarea curenta a lui k
In chenar ingrosat sunt incadrate secventele care se afiseaza.
Taie(4)
(2)
. -
k=1 Taie(3) k=2 Taie(2)
(1) (2) (1) (2)
. . . - - . - -
k=2 Taie(2) k=2 Taie(1) k=2 Taie(1) k=2 Taie(0)
(1) (2)
. . . . . - . - . - . . - -
k=3 Taie(1) k=3 Taie(0)
. . . . . . -
Fig.3.4.b. Arborele de apeluri al procedurii Taie(4)
Exemplul 3.4.b. Algoritm pentru determinarea tuturor solutiilor de iesire dintr-un labirint.
Algoritmul care va fi prezentat in continuare presupune un labirint
Labirintul este descris cu ajutorul unui tablou bidimensional de caractere de dimensiuni (n+1)*(n+1)
In tablou, cu ajutorul caracterului '*' sunt reprezentati peretii,
Cu ajutorul caracterului ' ' sunt reprezentate culoarele.
Punctul de start este centrul labirintului,
Drumul de iesire se cauta cu ajutorul unei proceduri recursive Cauta(x,y) unde x si y sunt coordonatele locului curent in labirint si in acelasi timp indici ai tabloului care materializeaza labirintul.
Cautarea se executa astfel:
Daca valoarea locului curent este ' '
Se intra pe un posibil traseu de iesire
Se marcheaza locul cu caracterul '#'.
Daca s-a ajuns la margine rezulta ca s-a gasit un drum de iesire din labirint si se executa afisarea tabloului bidimensional (labirintul si drumul gasit).
Daca valoarea locului curent nu este ' '
Se apeleaza recursiv procedura Cauta pentru cele patru puncte din vecinatatea imediata a locului curent, dupa directiile axelor de coordonate (dreapta, sus, stanga, jos).
Pentru fiecare cautare reusita traseul apare marcat cu '# '.
Marcarea asigura nu numai memorarea drumului de iesire dar in acelasi timp inlatura reparcurgerea unui drum deja ales.
Reluarea parcurgerii aceluiasi drum poate conduce la un ciclu infinit.
Este importanta sublinierea faptului ca marcajul de drum se sterge de indata ce s-a ajuns intr-o fundatura sau daca s-a gasit o iesire, in ambele situatii revenindu-se pe drumul parcurs pana la proximul punct care permite selectia unui nou drum.
Stergerea se executa prin generarea unui caracter ' ' pe pozitia curenta inainte de parasirea procedurii. Aceasta corespunde practic infasurarii 'firului parcurgerii' conform metodei 'firului Ariadnei'.
In secventa [3.4.c] este prezentata schita de principiu a procedurii Cauta iar in [3.4.d] o varianta de implementare Pascal
Procedura Cauta(x,y: coordonate);
daca *locul
este liber atunci [3.4.c]
*marcheaza locul
daca *s-a
ajuns la iesire atunci *afiseaza drumul
altfel
Cauta(x+1,y); Cauta(x,y+1);
Cauta(x-1,y); Cauta(x,y-1)
*sterge marcajul
PROCEDURE Cauta(x,y: integer);
BEGIN
IF m[x,y]=' ' THEN
BEGIN [3.4.d]
m[x,y]:= '#';
IF ((x MOD n)=0)OR((y MOD n)=0) THEN *afiseaza
ELSE
BEGIN
Cauta(x+1,y); Cauta(x,y+1); Cauta(x-1,y);
Cauta(x,y-1)
END;
m[x,y]:= ' '
END
END;
Procedura recursiva Cauta materializeaza metoda expusa anterior.
Daca in timpul cautarii se atinge una din extremele valorilor abscisei sau ordonatei ( sau n), s-a gasit o iesire din labirint si se realizeaza afisarea.
In figura 3.4.c se prezinta un exemplu de executie al acestei proceduri.
******* ******* ******* ******* ******* *******
* * * * * * * * * * * *
* ** ** * *** * * ** ** * *** * * ** ** * *** *
* * * * * * * * * * * * * * *
* * ******* * * * * ******* * * * * ******* * *
* * * *** * * * * *** * * * * *** *
* * * *** * * * * * * *** * * * * * * *** * * *
* * * * * * * * * * * *
*** ***** * * * *** ***** * * * *** ***** * * *
* * * * * * * * * * * *
* ********* * * * ********* * * * ********* * *
* * * * * * * * * * * *
* * ******* * * * * ******* * * * * ******* * *
* * * * * * * * * * * *
******* ******* ******* ******* ******* *******
Fig.3.4.c. Exemplu de executie al procedurii Cauta
Curbele recursive reprezinta un alt domeniu de aplicatie al algoritmilor recursivi.
Astfel de curbe pot fi generate cu ajutorul unui sistem de calcul, intrucat ele presupun un numar redus de module care se imbina succesiv, conform unor reguli simple, bine precizate.
Scopul acestui paragraf este acela de a prezenta doi algoritmi recursivi care permit generarea unor astfel de curbe.
Se face precizarea ca studiul curbelor recursive care aparent nu are o aplicabilitate practica imediata, contribuie in mod esential la fundamentarea, consolidarea si intelegerea conceptului de recursivitate.
Exemplul 3.a. Algoritm recursiv pentru generarea curbelor lui Hilbert.
In figura 3.a apar reprezentate patru curbe notate H0 , H1 , H2 si H3 care reprezinta curbele lui Hilbert de ordin 0, 1, 2 si 3.
Din figura se observa ca o curba Hilbert Hi+1
Se obtine prin compunerea a patru instante de curbe Hi ,
Cele 4 instante au dimensiunea injumatatita,
Ele sunt rotite in mod corespunzator,
Instantele sunt legate intre ele prin trei linii de legatura (prezentate mai ingrosat).
|
(A |
(A |
(A |
(A | ||||||||||||||||
|
H |
H |
H |
H | ||||||||||||||||
Fig.3.a. Curbele lui Hilbert de ordin 0, 1, 2 si 3
Se observa ca curba H1 poate fi considerata ca si constand din 4 instante al curbei vide H0 , unite prin aceleasi linii de legatura.
Acestea sunt curbele Hilbert datand din
Se presupune ca exista disponibila o biblioteca grafica care dispune de procedurile:
MoveTo(x,y) care pozitioneaza cursorul grafic in punctul de coordonate x,y;
LineTo(x,y) care traseaza o linie dreapta intre pozitia curenta si cea indicata prin x,y
In continuare ne propunem sa concepem un program simplu pentru reprezentarea grafica a curbelor Hilbert de diferite ordine.
Deoarece fiecare curba Hi consta din patru copii injumatatite Hi-1 , este normal ca procedura care-l deseneaza pe Hi sa fie compusa din patru parti, fiecare desenand cate o curba Hi-1 rotita corespunzator si la dimensiunea ceruta.
Cele patru parti sunt denumite A, B, C si D, iar rutinele care traseaza liniile sunt reprezentate prin sageti indicand directia de trasare.
Prin generalizare se deduc cele patru modele recursive care sunt prezentate in figura 3.b.
A B C D
|
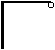
A |
D |
B |
B |
D |
C |
C |
A | |||||||||||
|
A |
B |
C |
A |
B |
C |
D |
D | |||||||||||
|
| ||||||||||||||||||
A D B B D C C A
Fig.3.b. Modele recursive pentru curbele lui Hilbert
Pornind de la aceste modele recursive se deduc imediat schemele recursive care permit generarea curbelor lui Hilbert [3.a].
A:D A A B
B:C B B A [3.a]
C:B C C D
D:A D D C
Daca lungimea unitatii de linie se noteaza cu h , procedura care corespunde modelului A poate fi redactata utilizand apeluri recursive la ea insasi precum si la procedurile D si B realizate in aceeasi maniera [3.b].
PROCEDURE A(i: integer);
BEGIN
IF i>0 THEN
BEGIN
D(i-1); x:= x-h; LineTo(x,y);
A(i-1); y:= y-h; LineTo(x,y); [3.b]
A(i-1); x:=
x+h; LineTo(x,y);
B(i-1)
END
END;
Procedura este initializata in programul principal pentru fiecare curba Hilbert care va fi supraimprimata.
Se considera ca pe acelasi desen se suprapun curbe Hilbert de mai multe ordine succesive.
Programul principal determina punctul initial de start al fiecarei curbe si incrementul specific h
Variabila h0 care precizeaza dimensiunea totala a paginii trebuie sa aiba valoarea 2k unde k > n n fiind ordinul maxim al curbelor care supraimprima.
Programul integral care traseaza curbele Hilbert H1 , H2 , , Hn apare in secventa [3.c].
PROGRAM Hilbert;
CONST n=4; h0=512;
VAR i,h,x,y,x0,y0: integer;
PROCEDURE B(i: integer); FORWARD;
PROCEDURE C(i: integer); FORWARD;
PROCEDURE D(i: integer); FORWARD;
PROCEDURE A(i: integer);
BEGIN
IF i>0 THEN
D(i-1); x:= x-h; LineTo(x,y);
A(i-1); y:= y-h; LineTo(x,y);
A(i-1); x:= x+h; LineTo(x,y);
B(i-1)
END
END; [3.c]
PROCEDURE B(i: integer);
BEGIN
IF i>0 THEN
BEGIN
C(i-1); y:= y+h; LineTo(x,y);
B(i-1); x:= x+h; LineTo(x,y);
B(i-1); y:= y-h; LineTo(x,y);
A(i-1)
END
END
PROCEDURE C(i: integer);
BEGIN
IF i>0 THEN
BEGIN
B(i-1); x:= x+h; LineTo(x,y);
C(i-1); y:= y+h; LineTo(x,y);
C(i-1); x:= x-h; LineTo(x,y);
D(i-1)
END
END;
PROCEDURE D(i: integer);
BEGIN
IF i>0 THEN
BEGIN
A(i-1); y:= y-h; LineTo(x,y);
D(i-1); x:= x-h; LineTo(x,y);
D(i-1); y:= y+h; LineTo(x,y);
C(i-1)
END
END;
BEGIN
i:= 0; h:= h0; x0:= h DIV 2; y0:= x0;
REPEAT
i:= i+1; h:= h DIV 2;
x0:= x0+(h DIV 2); y0:= y0+(h DIV 2);
x:= x0; y:= y0; MoveTo(x,y);
A(i)
UNTIL i=n;
END
Exemplul 3.b. Algoritm recursiv pentru trasarea curbelor lui Sierpinski.
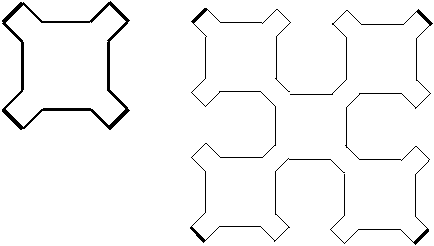
Un exemplu mai complicat il reprezinta curbele lui Sierpinski care apar in figura 3.c (S1 si S2).
A A
D B
C D B
(S
C2
(S
Fig.3.c. Modele recursive pentru curbele lui Sierpinski de ordin 1 si 2
Diferenta dintre curbele lui Sierpinski si cele ale lui Hilbert este aceea ca primele sunt curbe inchise.
Aceasta implica faptul ca modelul recursiv de baza trebuie sa fie o curba deschisa
Cele patru parti ale sale sunt conectate prin linii de legatura care nu apartin modelului recursiv propriu-zis.
Aceste legaturi constau in patru linii drepte situate in colturile figurii si care sunt reprezentate ingrosat in desen.
Din aceasta reprezentare rezulta clar modul de asamblare al curbelor de ordin inferior pentru a obtine o curba de ordin superior.
Pornind de la aceste observatii, pot fi construite cele patru modelele generice ale curbelor lui Sierpinski.
Ele sunt denumite A, B, C si D iar liniile de legatura sunt precizate explicit prin sageti (fig.3.d).
S: A B C D [3.d]
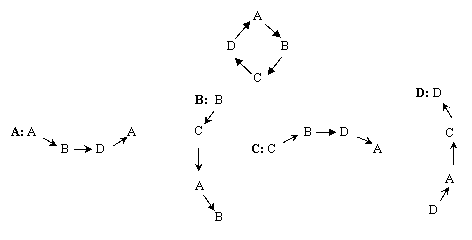
Fig.3.d. Modelele recursive ale curbelor lui Sierpinski
Cele patru modele grafice recursive sunt identice exceptand faptul ca sunt rotite cu 90s fiecare.
Este foarte important de subliniat faptul ca cele patru modele se asambleaza prin intermediul unui model de baza reprezentat in figura deasupra.
Din aceste modele pot fi deduse simplu schemele recursive care permit generarea curbelor.
In secventa [3.e] apar schemele recursive ale curbelor componente, unde o sageata dubla indica o linie de lungime dubla.
A :
A B T D A
B :
B C A B [3.e]
C :
C D B C
D :
D A C D
Considerand aceleasi facilitati de reprezentare ca si in cazul anterior pot fi redactate cu usurinta rutinele recursive care traseaza curbele lui Sierpinski.
Astfel, procedura A poate fi construita pornind de la prima linie a modelului recursiv precizat in [3.e] la fel si procedurile B,C si D
In secventa [3.f ] apare un model de implementare pentru procedura A
PROCEDURE A(i: integer);
BEGIN
IF i>0 THEN [3.f]
BEGIN
A(i-1); x:= x+h; y:= y-h; LineTo(x,y);
B(i-1); x:= x+2*h; LineTo(x,y);
D(i-1); x:= x+h; y:= y+h; LineTo(x,y);
A(i-1)
END
END;
Programul principal este conceput conform modelului [3.d].
Sarcina sa este aceea de a fixa valorile coordonatelor initiale conform cu dimensiunea zonei de afisare.
Programul integral apare in [3.g].
Eleganta si oportunitatea utilizarii recursivitatii in aceasta situatie este evidenta.
Corectitudinea programului poate fi usor dedusa din structura sa si din forma modelelor.
Limitarea adancimii recursivitatii s-a realizat cu ajutorul parametrului i, garantand in acest mod terminarea programului.
Utilizarea iteratiei in aceste situatii conduce la programe complicate si greoaie.
PROGRAM Sierpinski;
CONST n=4; h0=512;
VAR i,h,x,y,xo,yo: integer;
PROCEDURE B(i: integer); FORWARD;
PROCEDURE C(i: integer); FORWARD;
PROCEDURE D(i: integer]; FORWARD;
PROCEDURE A(i: integer);
BEGIN
IF i>O THEN
BEGIN
A(i-1); x:= x+h; y:= y-h; LineTo(x,y);
B(i-1); x:= x+2*h; LineTo(x,y);
D(i-1); x:= x+h; y:= y+h; LineTo(x,y);
A (i-1)
END
END;
PROCEDURE B;
BEGIN
IF i>0 THEN
BEGIN
B(i-1); x:= x-h; y:= y-h; LineTo(x,y);
C(i-1); y:= y-2*h; LineTo(x,y);
A(i-1); x:= x+h; y:= y-h; LineTo(x,y);
B(i-1)
END
END;
PROCEDURE C; [3.g]
BEGIN
END;
PROCEDURE D;
BEGIN
END;
BEGIN
i:= 0; h:= ho DIV 4; xo:= 2*h; yo:= 3*h;
REPEAT
i:= i+1; xo:= xo-h;
h:= h DIV 2; yo:= yo+h;
x:= xo; y:= yo; MoveTo(x,y);
A(i); x:= x+h; y:= y-h; LineTo(x,y);
B(i); x:= x-h; y:= y-h; LineTo(x,y);
C(i); x:= x-h; y:= y+h; LineTo(x,y);
D(i); x:= x+h; y:= y+h; LineTo(x,y)
UNTIL i=n;
END.
|
Politica de confidentialitate |
 .com |
Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
