APLICATII - Calcule trigonometrice
1. Calcularea punctelor auxiliare de-a lungul unei drepte
De-a lungul unei drepte apartinand unui contur, intre punctele P1 si P2 (P1: x = 15, z = 105; P2: x = 50, z = 62), se cere calculul valorii coordonatei z al unui punct auxiliar in punctul in care coordonata x are valoarea 30 (vezi Fig. 5.71.a). Un astfel de calcul poate fi necesar, de exemplu, atunci cand o operatie de degrosare necesita mai multe treceri. Problema se rezolva in urmatorii pasi :
Primul pas:
Trasand o paralela axei z prin punctele P1 si H si o alta paralela la axa X, care se intersecteaza cu punctul P2, se obtin doua triunghiuri dreptunghice suprapuse. Trebuie calculata distanta "b".
Al doilea pas:
Fig. 5.71 b indica faptul ca teorema asemanarii este aplicabila. Se aplica formula data de teorema asemanarii (Fig. 5.71 c)
Al treilea pas:
Cu ajutorul Fig. 5.71a, putem calcula valorile A, B si a cerute pentru a aplica teorema asemanarii (Fig. d)
A = 50 mm - 15 mm = 35 mm
B = 105 mm - 62 mm = 43 mm
C = 50 mm - 30 mm = 20 mm
Al patrulea pas:
Prin rearanjarea formulei teoremei asemanarii ![]() se obtine:
se obtine:
b = ![]()
Al cincilea pas:
Valoarea punctului H pe coordonata z se obtine (Fig. 5.72 e) prin adunarea valorii coordonatei punctului P2 pe axa Z si distanta b. Rezulta valoarea punctului H pe coordonata z = 62 mm + 24,57 mm = 86,57 mm
2: Calcularea lungimii generatoarei conului
O piesa strunjita (Fig. 5.73 a) are o zona conica intre punctele P1 si P2. Punctul P1 are coordonatele x = 15 si z = 85. Unghiul dintre generatoarea conului si axa z este α = 350. Numai coordonata x, adica 50, este cunoscuta pentru punctul P2. Sa se calculeze coordonata z.
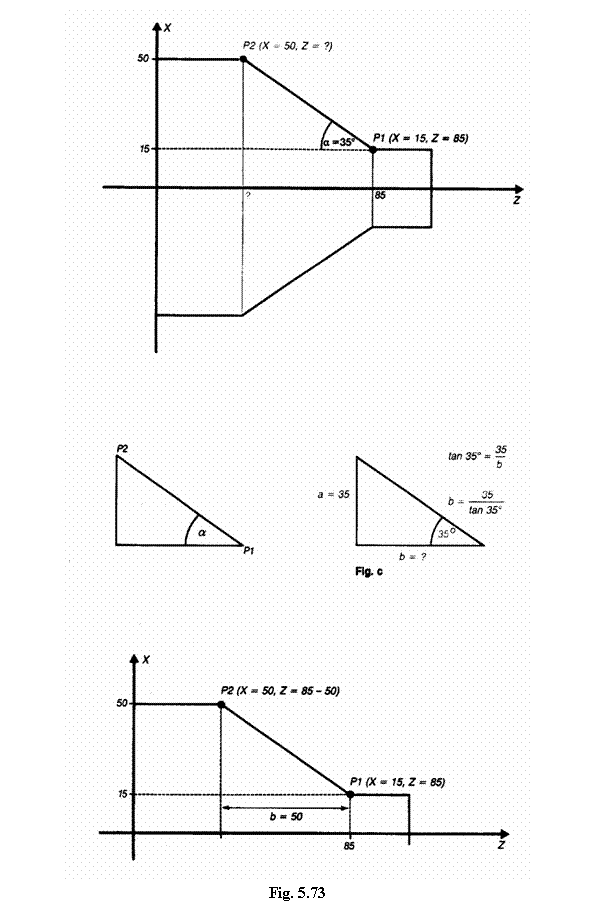
Primul pas:
Se traseaza doua paralele la axele x si z prin punctele P1 s P2, astfel incat problema sa poata fi rezolvata prin calcule trigonometrice (Fig.5.73 b)
Al doilea pas:
Din triunghiul prezentat in Fig.5.73 b se cunosc unghiul α si latura a. Trebuie sa se afle latura b. Pentru aflarea acesteia se aplica functia tan.
Al treilea pas:
Din formula functiei tan, se obtine b = ![]()
Introducand valorile laturii a si a unghiului α, se obtine
b = ![]()
Al patrulea pas:
Coordonata z a punctului P2 este obtinuta prin scaderea lungimii laturii b a triunghiului (Fig. 5.73 d) din coordonata z a punctului P1 ( z = 85)
Coordonata z a punctului P1 = 85 mm
Lungimea laturii b = 50 mm
Coordonata z a punctului P2 = 35 mm
3: Calcularea coordonatelor centrului cercului
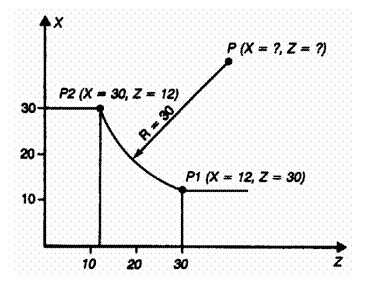
Intre punctele P1 si P2 ale unui contur frezat (Fig. 5.74 a) ( P1: x = 20, z = 70; P2: x = 45, z = 40), trebuie sa se frezeze un arc de cerc cu raza R = 50 mm. Sa se calculeze coordonatele centrului cercului ( presupunand ca sistemul de control poate permite doar programarea centrului cercului).
Primul pas:
Din triunghiul obtinut (Fig. 5.74 b) se poate calcula distanta intre P1 si P2 aplicand teorema lui Pitagora ( a2 + b2 = c2). Lungimile laturilor a si b rezulta din coordonatele punctelor P1 si P2.
a![]() + b
+ b![]() = c
= c![]() se obtine c1
=
se obtine c1
= ![]() ; a1 = 25
mm; b1 = 30 mm
; a1 = 25
mm; b1 = 30 mm
c1
= ![]() =
= ![]() = 39,05 mm
= 39,05 mm
Al doilea pas:
Calculul unghiului α1 (Fig.5.74 c) prin aplicarea functiei trigonometrice tan:
tan α1 = ![]() =
= ![]() =
=
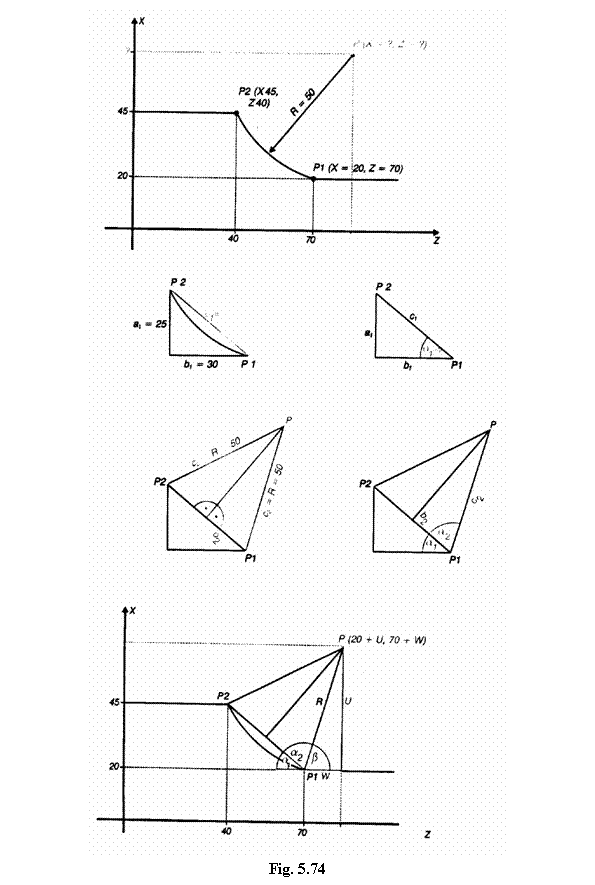
Al treilea pas:
Se formeaza triunghiul isoscel de-a lungul distantei de
corectie ![]() cu lungimile laturilor
R = 50 mm (Fig. 5.74 d) si se imparte acest triunghi in doua
triunghiuri dreptunghice congruente cu b2 = ½ c1 = 19,53
mm si c2 = 50 mm
cu lungimile laturilor
R = 50 mm (Fig. 5.74 d) si se imparte acest triunghi in doua
triunghiuri dreptunghice congruente cu b2 = ½ c1 = 19,53
mm si c2 = 50 mm
(Punctul P reprezinta centrul cercului dorit)
Al patrulea pas:
Calculul unghiului α2 prin aplicarea functiei trigonometrice cos (Fig.5.74 e)
cos α2 = ![]() =
= ![]() = 0,39 se obtine α2 = 67,010
= 0,39 se obtine α2 = 67,010
Al cincilea pas:
Se aduna unghiurile α1 si α2 (Fig. e)
Al saselea pas:
Calculul distantelor punctului P spre punctul P1 in directia x si z (Fig. f)
Distanta in directia x: U = R x sin β = 50 mm x sin 73,180 = 50 mm x 0,96 = 47,86 mm (sin β = U/R)
Distanta in directia z: W = R x cos β = 50 mm x cos 73,180 = 50 mm x 0,29 = 14,47 mm
Al saptelea pas:
Calculul coordonatelor punctului P al centrului cercului din coordonatele punctului P1 (x = 20, z = 70) si valorile lui U si W:
x = 20 + U = 20 + 47,86 = 67,86
z = 70 + W = 70 + 14,47 = 84,47
Exercitii pentru modulul "Calcule trigonometrice"
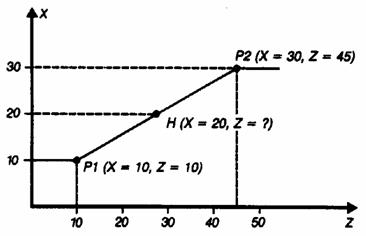
 1. Calculul coordonatei Z a punctului H:
1. Calculul coordonatei Z a punctului H:
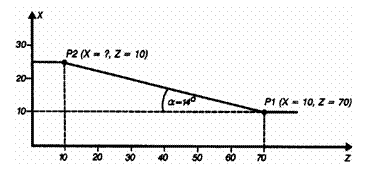
2. Calculul coordonatei X a punctului P2:
3. Calculul coordonatelor centrului cercului:
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |