Toate gramaticile cu care vom lucra in acest sunt independente de context; de aceea nu vom mai specifica explicit acest lucru.
Fie G=(VN,VT,S,P) o gramatica (independenta de context).
Analiza sintacticǎ constǎ in urmatoarele:
se dǎ 
;
se cere sǎ se determine dacǎ wIL(G) si, in caz afirmativ, sǎ se determine productiile care trebuie aplicate pentru a obtine o derivare stangǎ a lui w din S
Observatie. Daca productiile au numere de ordine, sirul numerelor de ordine ale productiilor ce trebuie aplicate este numit sintaxa stanga a lui w. Ea este importanta, deoarece pe baza ei se poate construi usor arborele de derivare asociat lui w
Vom folosi urmatoarele conventii de notatii:
a,b,c, I VT
A,B,C, I VN
x,y,z,u,v,w,I
a b g I
si se va specifica explicit cand ele sunt incǎlcate.
In continuare considerǎm cǎ in G nu apar neterminale 'nefolositoare', adica:
din orice neterminal deriva un cuvant format numai din terminale (neterminalul este observabil);
pentru orice neterminal exista o derivare din S in care apare acel neterminal (neterminalul este accesibil).
Stim ca pentru orice gramatica independenta de context exista una echivalenta de acelasi tip, in care nu apar neterminale nefolositoare, deci presupunerea facuta nu este restrictiva.
De asemenea, toate derivarile care vor aparea in continuare sunt derivari stangi (stim ca existenta unei derivari este echivalenta cu existenta unei derivari stangi).
In sfarsit, inchiderea tranzitiva si reflexiva a relatiei de derivare T va fi notata tot prin T, pentru a nu incarca scrierea.
Definim doua functii cu care vom lucra in continuare.
j : (VN VT)* P(VT (prin P am notat multimea partilor), data de:
j a
Functia j mai poarta numele FIRST
Caz
particular: pentru 
j a , unde a este prima
literǎ din a (dacǎ a l) sau este l (dacǎ a l
Definitia
functiei j se poate extinde la multimi de cuvinte din 
. Pentru 
definim: j(L)=
Definim functia 
prin:
Definitie. G este o gramaticǎ LL(1) dacǎ:
adicǎ, dat fiind un cuvant wAa si un terminal a, existǎ cel mult o productie (cu A in membrul stang) care se poate aplica astfel incat in final sǎ se obtinǎ un cuvant format din terminale in care imediat dupǎ w sǎ aparǎ a.
Teoremǎ. G este de tip LL(1) 
distincte, avem 
.
Fie
Cum 
, conform ipotezei, avem: .
Dar 
, deci 
. Contradictie.
T Fie
distincte.
Presupunem cǎ 
.
Dacǎ a I VT avem patru situatii:
deci 
w,a cu 
(nu existǎ
neterminale nefolositoare)
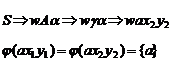T 
. Contradictie.
2) 
adicǎ 
, deci 
cu si 
T b g. Contradictie.
3) 
Se face la fel ca la 2).
4) 
Deci cu cu 
T b g Contradictie.
Dacǎ a = l
Atunci avem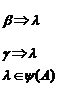 
si deci w, a cu 
si 
, adicǎ 
.
T b g Contradictie.
l l
Corolar. G este LL(1) 
, 
pentru i j; daca 
.
Traducatorul sintactic
Este asemǎnǎtor unui automat push-down. Are insǎ in plus o bandǎ de iesire si functioneazǎ pe baza unui tabel de analizǎ sintacticǎ conform unui algoritm sintactic.
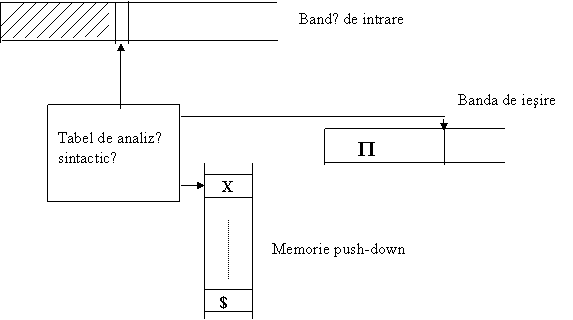
Dacǎ G este o gramaticǎ LL(1), atunci:
pe banda de intrare apar cuvinte 
;
pe banda de iesire apar
siruri 
formate din numerele
de ordine ale productiilor din gramaticǎ;
in memoria pushdown apar cuvinte
de forma 
$ cu 
.
Prin configuratie intelegem un triplet (x, a p unde:
este cuvantul care a
mai rǎmas de citit de pe banda de intrare;
a este cuvantul din memoria p.d.;
p este sirul aflat pe banda de iesire.
Configuratia initialǎ este (w, S$, l unde w este cuvantul care trebuie analizat sintactic.
Trecerea de la o configuratie la alta este datǎ de algoritmul sintactic pe baza tabelului de analizǎ sintacticǎ
Tabelul de
analiza sintactica este o functie M definita pe 
.
Pentru gramaticile de tipul LL(1) vom defini acest tabel conform regulilor:
Fie 
. Definim 
pentru 
. Dacǎ in plus , definim 
.
SALT
DA
In rest, 
=NU.
Observatie: Fie . Atunci 
Aceastǎ observatie aratǎ, pe baza corolarului precedent, cǎ functia M este bine definitǎ.
|
M |
a |
b |
l |
S |
aAS,1 |
b,2 |
|
A |
a,3 |
bSA,4 | |
|
a |
SALT | ||
|
b |
SALT | ||
|
DA |
Exemplu
1) 
2) 
3) 
4) 
Pentru gramaticile LL(1) definim urmǎtorul algoritm sintactic:
1) 
| 
dacǎ 
, adicǎ 
2) 
| 
, ceea ce corespunde situatiei SALT
3) Algoritmul se terminǎ dacǎ:
3.1) se ajunge la 
; se aplicǎ deci DA
3.2) se ajunge la cu 
NU.
Exemplu. Pentru gramatica de mai sus:
| 
| 
| (bbab,bSAS$, (bab,SAS$,
| (bab,bAS$, (ab,AS$,
| (ab,aS$, (b,S$,
| (b,b$, l
deci w=abbabIL(G) si sintaxa sa stanga este p
Fie acum un tabel de analizǎ sintacticǎ M oarecare si fie A un algoritm sintactic construit pe
baza acestui tabel. Atunci pentru 
definim
,dacǎ 
|
nedefinit , in caz contrar
1) 
|
2) Dacǎ da, 
.
Definitie. Algoritmul A este corect dacǎ :
1) 
Dacǎ A(w) = p atunci p este sintaxa stangǎ a lui w
(adicǎ 
).
Definitie. Tabelul M este corect dacǎ algoritmul construit pe baza lui este corect.
Remarcǎm cǎ in cazul unui tabel si a unui algoritm corecte, algoritmul se opreste intr-una dintre situatiile:
w I L(G), adicǎ w este "corect sintactic"; in acelasi timp este furnizatǎ sintaxa lui;
w L(G), adicǎ w "nu este corect sintactic"; in aceastǎ situatie va trebui produs un mesaj de eroare.
Teoremǎ. Algoritmul sintactic si tabelul de analizǎ sintacticǎ definite mai sus pentru gramaticile LL(1) sunt corecte
Demonstratia cuprinde doi pasi.
:
Demonstratia se face prin inductie dupǎ numǎrul n de schimbǎri de configuratie.
Pentru n = 1
(xy, S$, l (y, a p implicǎ x = l p = i, M(S, j(y)) = (a, i) unde
. Rezultǎ .
n
(xy, S$, l (ay, b p (y, a p , unde aI VT . Implicǎ x = x'a.
|
.
Daca a = l, atunci b = Ag a dg p p'i, 
. Rezultǎ 
.
Daca a l , atunci b = aa p p si 
.
| (y,
a p y cu j(y) j a , unde a este fie l, fie incepe cu un neterminal.
i
. Fie y cu j(y) j a
x l : (xy, S$, l (xy, xa l pentru cǎ j(xy) j(xay(S))
| (y, a p
2) x = l : (y, S$, l (y, a$, i) pentru cǎ j(y) j a j ay(S))
n n+1
a x1
A
cu p p'i (am pus in evidenta
ultimul pas)
| (y, a p
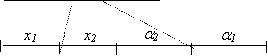
Cf. ipotezei de inductie, pentru z cu j(z) j(Aa , avem : (x, z, S$, l (z, Aa p
Luam z = x2y.
Atunci j(x2y) j(Aa deoarece j(x2y) j(x2a j(Aa pt. ca Aa T x2a a = x2a
Deci (x1x2y, S$, l (x2y, Aa p
= x
? dacǎ j(x2y) j(x2a y(A))
dacǎ x2 l, evident
dacǎ
x2 = l trebuie j(y) j a y(A)). Dar j(y) j a j a a j a j a j a y(A)) pentru cǎ 
.
Inlocuind acum y = a l in pasii notati cu , sse obtine rezultatul din enuntul teoremei.
Aplicatie
Consideram urmatoarea gramatica ce genereaza expresiile aritmetice corecte in care apare variabila a, operatiile binare si , precum si cuprinderea intre paranteze.
S S+T
S T
T T*F
T F
F (S)
F a
Este evident ca aceasta gramatica nu este de tipul LL(1). Ea poate fi adusa insa la o gramatica de tipul LL(1), folosind faptul ca ansamblul de productii:
A Aa
A b
este echivalent cu ansamblul de productii:
A bA'
A' aA'
A' l
Obtinem astfel urmatoarea gramatica echivalenta de tipul LL(1):
S TE
E +TE
E l
T FU
U *FU
U l
F (S)
F a
Tabelul de analiza sintactica este urmatorul:
|
a |
l |
|||||
|
S |
TE,1 |
TE,1 | ||||
|
E |
l |
+TE,2 |
l |
|||
|
T |
FU,4 |
FU,4 | ||||
|
U |
l |
l |
*FU,5 |
l |
||
|
F |
a,8 |
(S),7 | ||||
|
a |
SALT | |||||
|
SALT | ||||||
|
SALT | ||||||
|
SALT | ||||||
|
SALT | ||||||
|
DA |
Sa consideram cuvantul w=(a*a) si sa aplicam algoritmul sintactic:
[(a*a),S$,l [(a*a),TE$,1] ├ [(a*a),FUE$,14] ├
[(a*a),(E)UE$,147] ├ [a*a),E)UE$,147] ├
[a*a),TE)UE$,1471] ├ [a*a),FUE)UE$,14714]├
[a*a),aUE)UE$,147148] ├ [*a),UE)UE$,147148]├
[*a),*FUE)UE$,1471485] ├ [a),FUE)UE$,1471485]├
[a),aUE)UE$,14714858] ├ [),UE)UE$,14714858]├
[),E)UE$,147148586] ├ [),)UE$,1471485863] ├
l,UE$,1471485863] ├ l,E$,14714858636] ├
l
Rezulta ca w este corect ( adica wIL(G) ) si sintaxa sa stanga este p , pe baza caruia putem construi arborele de derivare.
Observatie. De fapt am redus problema la determinarea functiilor j si y, sarcina ce nu este deloc facila!
|
Politica de confidentialitate |
 .com |
Copyright ©
2024 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |
