
NUMERE COMPLEXE SUB FORMA TRIGONOMETRICA
Fie ![]() ,
, ![]() ,
, ![]() si
si ![]()
Daca numerele complexe ![]() sunt scrise sub forma trigonometrica, avem:
sunt scrise sub forma trigonometrica, avem:
![]()
![]()
![]()
sau
![]()
![]()
Formula lui Moivré:
Pentru orice ![]() avem
avem ![]()
Radacina de ordin n dintr-un numar complex:
![]()
Argumentul nr.C
Se noteaza cu θ sau cu argZ si este prin definitie unghiul format de OM cu axa OX si orientat trigonometric:
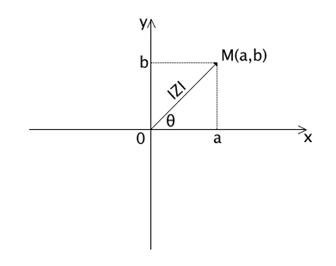
Argumentul unui numar complex ![]() este unic determinat
si este dat de
este unic determinat
si este dat de ![]()
Conjugatul numarului C
Fie ![]() , notam conjugatul cu
, notam conjugatul cu ![]() . Avem echivalenta
. Avem echivalenta ![]()
Puterile numarului i
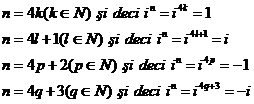
Puterile cu exponent natural ale lui i sunt
elementele multimii ![]()
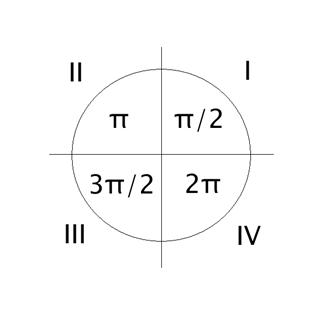
a) cadranul I: ![]()
b) cadranul II: ![]()
c) cadranul III: ![]()
d) cadranul IV: ![]()
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |