
secvenTe numerice 1D Si 2D
Obiectivele lucrarii
1) Asimilarea functiilor MATLAB specifice lucrului cu secvente discrete 1D si 2D;
2) Deprinderea tehnicilor de analiza a secventelor discrete in domeniile temporal si spectral;
3) Studiul interactiv al proprietatilor secventelor discrete si al operatorilor aplicati acestora utilizand mediul DIDACTICIEL.
Desfasurarea lucrarii
Esantionarea semnalelor continue
Sa se
reprezinte formele de unda pentru un semnal sinusoidal continuu ![]() si varianta sa
esantionata (in timp discret)
si varianta sa
esantionata (in timp discret) ![]() , stiind ca:
, stiind ca:
![]()
Semnalul esantionat se scrie:
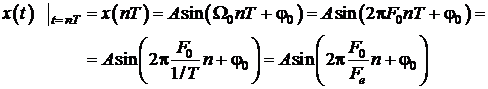
Se obtine deci:
![]()
unde: ![]() .
.
Deoarece ![]() si
si ![]() , rezulta:
, rezulta:
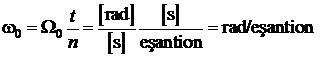
O imagine grafica sugestiva asupra corespondentelor in frecventa dintre domeniile timp continuu si timp discret este redata in figura 1.1.
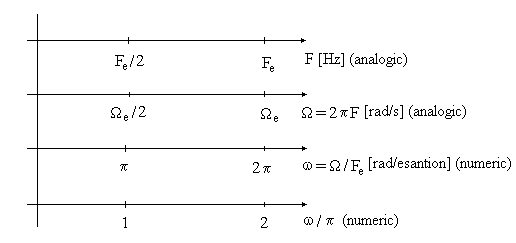
Figura
1.1
Codul MATLAB urmator reprezinta formele de unda pentru un semnal sinusoidal continu si discret, pentru urmatorii parametri:
![]()
Fe=16e3; t=0:1/Fe:5e-3; n=0:length(t)-1;
subplot(211); plot(t,10*sin(2 pi*1200*t+pi/4));
xlabel('timp continuu'); ylabel('amplitudine')
title('Semnal sinusoidal continuu')
subplot(212); stem(10*sin(2*pi*(1200/16000)*n+pi/4))
xlabel('timp discret'); ylabel('amplitudine')
title(' Semnal sinusoidal discret')
Secvente elementare
Sa se genereze si sa se reprezinte grafic secventele numerice 1D elementare urmatoare:
a) impuls Dirac ![]() ,
,
b) semnal treapta unitate ![]() ,
,
c) semnal poarta ![]() ,
,
d) semnal sinusoidal cu frecventa 1 KHz
esantionat la 10 KHz ![]() ,
,
e) semnal sinus cardinal ![]() ,
,
f) semnal exponential ![]() ,
,
g) semnal putere ![]() ,
,
f) semnal logaritm natural ![]() ,
,
h) semnal aleator cu repartitie normala cu media 1.5 si dispersia 0.25.
f=figure('Units','Norm','Position',[.01 .01 .98 .95]);
set(f,'MenuBar','none'); a1=axes('Position',[.05 .7 .25 .25]);
stem([zeros(1,14) 1 zeros(1,5)]);
set(a1,'YLim',[0 1.5],'XTick',[0:5:20],
'XTickLabel',[-10:5:10],'FontSize',8);
legend('Impuls Dirac',2)
a2=axes('Position',[.35 .7 .25 .25]);
stem([zeros(1,10) ones(1,10)]);
set(a2,'YLim',[0 1.5],'XTick',[0:5:20],
'XTickLabel',[-10:5:10],'FontSize',8);
legend('Semnal treapta unitate',2)
a3=axes('Position',[.65 .7 .25 .25]);
stem([zeros(1,12) ones(1,5) zeros(1,3)]);
set(a3,'YLim',[0 1.5],'XTick',[0:5:20],
'XTickLabel',[-10:5:10],'FontSize',8);
legend('Semnal poarta',2)
a4=axes('Position',[.05 .4 .25 .25]);
stem(sin(2*pi*.1*[0:20]+pi/4));
set(a4,'XLim',[0 20],'YLim',[-1 2],'XTick',[0:10:20],
'XTickLabel',[0:10:20]*1e-4,'FontSize',8);
legend('Semnal sinusoidal',2)
a5=axes('Position',[.35 .4 .25 .25]);
stem(sinc(.25*[-9:10]));
set(a5,'XLim',[0 20],'YLim',[-.25 1.5],'XTick',[0:5:20],
'XTickLabel',[-10:5:10],'FontSize',8);
legend('Semnal sinc',2)
a6=axes('Position',[.65 .4 .25 .25]);
stem(exp(-(0:20)));
set(a6,'YLim',[0 1.2],'XLim',[1 21],'XTick',[1:5:21],
'XTickLabel',[0:5:20],'FontSize',8);
legend('Semnal exponential e^-^n',2)
a7=axes('Position',[.05 .1 .25 .25]);
stem(pow2(-0.5*(0:20)))
set(a7,'YLim',[0 1.2],'XLim',[1 21],'XTick',[1:5:21],
'XTickLabel',[0:5:20],'FontSize',8);
legend('Semnal putere 2^-^0^.^5^n',2)
a8=axes('Position',[.35 .1 .25 .25]);
stem(log([.1:.1:2]))
set(a8,'YLim',[-3 3],'XLim',[0 20],'XTick',[0:5:20],
'XTickLabel',[0:.5:2],'FontSize',8);
legend('Semnal logaritm natural',2)
a9=axes('Position',[.65 .1 .25 .25]);
stem(1.5+.5*randn(1,20))
set(a9,'YLim',[0 4],'XLim',[0 20],'XTick',[0:5:20],
'XTickLabel',[-10:5:10],'FontSize',8);
legend('Semnal aleator normal',2)
In cazul ultimului semnal, sa se verifice valorile mediei si dispersiei. Ce valoare are puterea semnalului ?
Secvente complexe
Sa se genereze semnalul:
![]() ,
,
unde: K=2,
![]() ,
, ![]() .
.
c = -(1/12)+(pi/6)*i;
K = 2; n = 0:40;
x = K*exp(c*n);
subplot(2,1,1);
stem(n,real(x));
xlabel(' Index temporal n');
ylabel('Amplitudine');
title('Parte reala');
subplot(2,1,2);
stem(n,imag(x));
xlabel(' Index temporal n');
ylabel('Amplitudine');
title('Parte imaginara');
Care este semnificatia partii reale si a partii imaginare a lui c ?
Secvente modulate
Sa se genereze semnalul modulat in amplitudine:
![]()
unde: m= 0.4, ![]() ,
, ![]() .
.
n = 0:100 ; m = 0.4 ; fh = 0.1 ; fb = 0.01 ;
xh = sin(2*pi*fh*n) ; xb = sin(2*pi*fb*n) ;
y = (1+m*xb).*xh ; stem(n,y) ; grid ;
xlabel(' Index temporal n') ; ylabel('Amplitudine');
Reprezentarea secventelor numerice 1D si 2D folosind seria Fourier in timp discret (SFTD)
O secventa
1D periodica ![]() poate fi
reprezentata reprezentata prin seria Fourier in timp discret 1D (
poate fi
reprezentata reprezentata prin seria Fourier in timp discret 1D (![]() ):
):
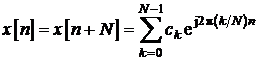
unde:
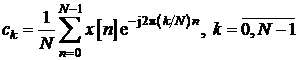
In mod similar,
o secventa 2D periodica ![]() poate fi reprezentata prin seria Fourier in timp
discret 2D (
poate fi reprezentata prin seria Fourier in timp
discret 2D (![]() ):
):
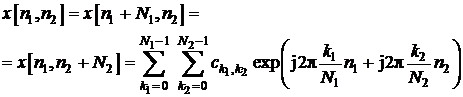
unde:
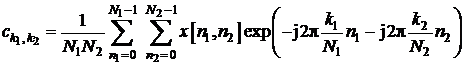 ,
, 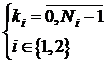
a) Sa se
realizeze descompunerea in ![]() a unei serii de
impulsuri periodice cu factorul de umplere 0.5. Motivul de baza va fi
definit folosind 64 de esantioane. Sa se verifice apoi
proprietatile generale ale coeficientilor descompunerii in
a unei serii de
impulsuri periodice cu factorul de umplere 0.5. Motivul de baza va fi
definit folosind 64 de esantioane. Sa se verifice apoi
proprietatile generale ale coeficientilor descompunerii in ![]() a unei secvente
periodice, cu valori reale, pentru care:
a unei secvente
periodice, cu valori reale, pentru care:
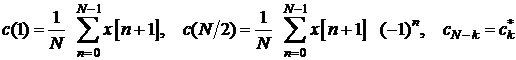
b) Sa se realizeze
descompunerea in ![]() a unei secvente
2D periodice al carei motiv de baza este definit de o
secventa rectangulara unitara de 8 8, avand
un suport 2D de 16
a unei secvente
2D periodice al carei motiv de baza este definit de o
secventa rectangulara unitara de 8 8, avand
un suport 2D de 16
a)
x=[ones(1,32),zeros(1,32)];N=64;
for k=0:N-1
c(k+1)=0;
for n=0:N-1
c(k+1)=c(k+1)+x(n+1)*exp(-j*pi*2*k/N*n);
end
c(k+1)=c(k+1)/N
end
stem(abs(c(1:N/2)))
b)
x=zeros(16);x(1:8,1:8)=ones(8);c=zeros(16);N=16;
for k1=0:N-1
for k2=0:N-1
for n1=0:N-1
for n2=0:N-1
c(k1+1,k2+1)=c(k1+1,k2+1)+x(n1+1,n2+1)*
exp(-j*2*pi*k1/N*n1-j*2*pi*k2/N*n2);
end
end
end
end
c=abs(c)
Teorema esantionarii
1. Sa se genereze un semnal de 0.5 s compus din suma a doua sinusoide de frecvente 100 Hz si 156 Hz cu amplitudinea de 1V. Se considera o frecventa de esantionare de 256 Hz. Reprezentati semnalul suma. Comentati rezultatul.
2. Sa se genereze, sa se reprezinte si sa se compare doua sinusoide de frecvente 100 Hz si 356 Hz si amplitudinea de 1V. Se considera o frecventa de esantionare de 256 Hz.
t=(1:128); f1=100; f2=156;fe=256;
y=sin(2*pi*f1/fe*t)+sin(2*pi*f2/fe*t);
plot(t/fe,y); xlabel('timp (s)') ; ylabel('amplitudine (V)')
t=(1:100); f1=100; f2=356; fe=256;
y1=sin(2*pi*f1/fe*t); y2=sin(2*pi*f2/fe*t);
subplot(211); plot(t/fe,y1); ylabel('amplitudine (V)');
title('sinusoida de frecventa 100 Hz')
subplot(212); plot(t/fe,y2);
xlabel('timp (s)'); ylabel('amplitudine (V)');
title('sinusoida de frecventa 356 Hz')
Semnalul chirp
Semnalul chirp , de durata T, are expresia: ![]() , unde faza instantanee este data de:
, unde faza instantanee este data de: ![]() . Rezulta ca frecventa instantanee a
semnalului chirp,
. Rezulta ca frecventa instantanee a
semnalului chirp, ![]() , variaza liniar pe durata T, conform relatiei:
, variaza liniar pe durata T, conform relatiei: ![]() , sau:
, sau: ![]() .
.
Secventa
MATLAB urmatoare analizeaza in domeniile temporal si
frecvential un semnal chirp, a
carui frecventa instantanee variaza intre 0 si 5 MHz, pe o durata ![]() . Frecventa de esantionare utilizata este
. Frecventa de esantionare utilizata este ![]() .
.
f0=0;ff=5e6; T=1e-5; beta=(ff-f0)*pi/T; Fe=5e7;t=0:1/Fe:T;
x=cos(2*pi*f0*t+beta*t.^2);
subplot(211),plot(t,x),
xlabel('timp [s]'); ylabel('amplitudine [V]');
title('semnal temporal')
X=abs(fft(x,1024));
subplot(212), plot([0:99]/Fe,X(1:100))
xlabel('frecventa [Hz]'); ylabel('amplitudine [V]');
title('spectrul semnalului')
Transformata Fourier discreta in timp discret (TFTD)
Sa se
elaboreze o functie MATLAB pentru calculul TFTD a unei secvente finite,
de lungime ![]() , pentru
, pentru ![]() frecvente
echidistante pe cercul unitate. Sa se utilizeze functia creata
pentru calculul TFTD a secventei
frecvente
echidistante pe cercul unitate. Sa se utilizeze functia creata
pentru calculul TFTD a secventei ![]() in
in ![]() puncte.
puncte.
function [H,W]=tftd(h,N)
W=(2*pi/N)*[0:N-1]'; mid=ceil(N/2)+1;
W(mid:N)=W(mid:N)-2*pi; W=fftshift(W);
H=fftshift(fft(h,N));
nn=0:40; xn=0.88.^nn;
[X,W]=tftd(xn,128);
subplot(211),plot(W/2/pi,abs(X))
xlabel('frecventa normalizata')
ylabel('amplitudine [V]')
subplot(212),plot(W/2/pi,180/pi*angle(X))
xlabel('frecventa normalizata')
ylabel('faza [grade]')
Transformata Hilbert
Fie
secventa reala: 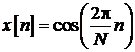 . Transformata sa Hilbert notata
. Transformata sa Hilbert notata ![]() - constituie partea
imaginara a secventei analitice:
- constituie partea
imaginara a secventei analitice: ![]() . Sa se determine transformata Hilbert a unui semnal
cosinusoidal.
. Sa se determine transformata Hilbert a unui semnal
cosinusoidal.
N=64;n=0:N-1;
x=cos(2*pi/N*n); stem(x) ;
y=hilbert(x);
subplot(211);stem(real(y));
title('Semnalul real');
xlabel('n');ylabel('Amplitudine');
subplot(212);stem(imag(y));
title('Transformata Hilbert a semnalului');
xlabel('n'); ylabel('Amplitudine');
Functia
pondere ![]() a unui transformator
Hilbert si functia sa de transfer pot fi obtinute astfel:
a unui transformator
Hilbert si functia sa de transfer pot fi obtinute astfel:
for nn=-31:1:32;
h(nn+32)=2*pi./nn.*((sin(pi*nn/2)).^2);
end
h(32)=0;[H,f]=freqz(h);
amp=20*log10(abs(H));
phase=unwrap(angle(H))*180/pi;
subplot(311); stem(h);
title('Functia pondere'); xlabel('n')
subplot(312); semilogy(f,amp);
xlabel('Pulsatie normalizata');
ylabel('Amplitudine (dB)'); grid
subplot(313); plot(f,phase);
xlabel('Pulsatie normalizata');
ylabel('Faza (grade)'); grid
Functia pondere a unui transformator Hilbert poate fi, de asemenea, obtinuta folosind:
h=remez(64,[0.1,0.9],[1,1], 'Hilbert');
Secvente 2D
Secventa 2D:
x
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 1 1 1 1];
reprezinta o imagine binara, sub forma unui patrat negru pe un fond alb. Vizualizati aceasta imagine. Calculati apoi TFD2D a matricii si vizualizati rezultatul acestei transformari. Comentati.
x=[1 1 1 1 1;1 0 0 0 1;1 0 0 0 1;1 0 0 0 1;1 1 1 1 1];
Xf=fft2(x);Xfsh=fftshift(Xf);
subplot(221);
imagesc(x);
title('imagine initiala ')
subplot(222);
imagesc(log(abs(Xf)));
title('Modulul spectrului imaginii')
subplot(223);
imagesc(log(abs(Xfsh)));
title('Modulul spectrului simetrizat al imaginii')
subplot(224);
imagesc(unwrap(angle(Xf)));
title('Faza spectrului imaginii') ;
colormap(gray)
Analiza Fourier a secventelor 2D
Incarcati imaginile "Clown" si "Gatlin2" sub MATLAB. Reprezentati spectrele celor doua imagini si apoi reconstruiti cele doua imagini interschimband spectrele de faza ale acestora.
load clown ; x = X;load gatlin2 ; y = X;
l = min(size(x,1),size(y,1));
c = min(size(x,2),size(y,2));
x = x(1:l,1:c);y = y(1:l,1:c);
X=fft2(x) ; Y=fft2(y);
Z1 = abs(X).*exp(i*angle(Y));
Z2 = abs(Y).*exp(i*angle(X));
z1 = real(ifft2(Z1));
z2 = real(ifft2(Z2));
figure(1)
fh = ([1:l]-l/2)/l;fv = ([1:c]-c/2)/c;
subplot(3,2,1); image(x); axis('image');
title('imagine x'); axis off
subplot(3,2,2); image(y); axis('image');
title('imagine y'); axis off
subplot(3,2,3);
imagesc(fh,fv,log(abs(fftshift(X.^2))));
axis('image'); title('Modul X');
xlabel('frecvente orizontale');
ylabel('frecvente verticale')
subplot(3,2,4);
imagesc(fh,fv,log(abs(fftshift(Y.^2))));
axis('image'); title('Modul Y');
xlabel('frecvente orizontale');
ylabel('frecvente verticale')
subplot(3,2,5);
imagesc(fh,fv,angle(fftshift(X))); axis('image');
title('Faza X');xlabel('frecvente orizontale');
ylabel('frecvente verticale')
subplot(3,2,6);
imagesc(fh,fv,angle(fftshift(Y)));
axis('image'); title('Faza Y')
xlabel('frecvente orizontale');
ylabel('frecvente verticale')
figure(2) ;
subplot(2,2,1); image(x); axis('image');
title('imagine x'); axis off
subplot(2,2,2); image(y); axis('image');
title('imagine y'); axis off
subplot(2,2,3); image(z1);
axis('image'); axis off
title('imagine: modul x + faza y')
subplot(2,2,4); image(z2);
axis('image'); axis off
title('imagine: modul y + faza x');colormap('gray')
Concluzionati in privinta importantei spectrului de faza pentru reconstructia imaginilor.
Studiul secventelor numerice utilizand mediul DIDACTICIEL
1) Se lanseaza DIDACTICIEL-ul prin introducerea comenzii:
didact
2) Se studiaza interactiv proprietatile diverselor secvente numerice cu ajutorul meniurilor definite in:
Signal generator
Numerical signals
Random signals
Tema
Verificati
proprietatea de liniaritate a ![]() :
:
![]()
folosind urmatoarele semnale:

si
considerand ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |