
REPARTITIA NORMALA MULTIDIMENSIONALA
Fie X ~ N m, Σ) vector aleator normal (gasussian) n-dimensional.
Consideram partitionarea in doi subvectori:
X = 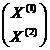 si
corespondentele din m =
si
corespondentele din m = ![]() si Σ =
si Σ = 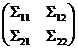 .
.
Atunci:
X(1) ~ N m - Σ12 ![]() m , Σ11.2), unde Σ11.2
= Σ11 - Σ12
m , Σ11.2), unde Σ11.2
= Σ11 - Σ12 ![]() Σ21.
Σ21.
X(2) ~ N m
iar functia de regresie a lui X(1) in raport X(2) este
E[X(1) / X(2)= x(2)] = m + Σ12 ![]() (x(2)-m
(x(2)-m
Exemplul 1: Fie X = ![]() ~ N m, Σ) , unde m =
~ N m, Σ) , unde m = ![]() , Σ =
, Σ =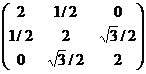
a) sa se determine
functiile de densitate marginala pentru X2 si ![]() .
.
Aici X(1)
= X2, X(2)
= ![]() si:
si:
m = (liniile din m conform X(1) = X2, adica a doua linie) = 1
m = (liniile din m conform X(2) = ![]() , adica linia 1 si 3) =
, adica linia 1 si 3) = ![]()
= (liniile din Σ conform X(1) = X2 si coloanele tot conform X(1) = X2, adica linia 2 si coloana 2) = 2
= (liniile din Σ conform X(1) = X2
si coloanele conform X(2) =
![]() , adica linia 2 si coloanele 1 si 3) =
(1/2
, adica linia 2 si coloanele 1 si 3) =
(1/2 ![]() /2)
/2)
= (liniile din Σ conform X(2) = ![]() si coloanele
conform X(1) = X2, adica liniile 1
si 3 si coloana 2) =
si coloanele
conform X(1) = X2, adica liniile 1
si 3 si coloana 2) = ![]()
= (liniile din Σ conform X(2) = ![]() si coloanele tot
conform X(2) =
si coloanele tot
conform X(2) =![]() , adica liniile 1 si 3 si coloanele 1 si
3) =
, adica liniile 1 si 3 si coloanele 1 si
3) = ![]() .
.
Deci m m =![]() , Σ11 =
2, Σ12 = (1/2
, Σ11 =
2, Σ12 = (1/2 ![]() ), Σ21=
), Σ21=![]() , Σ22=
, Σ22=![]() .
.
Inlocuim parametrii repartitiei lui X(1) ~ N m - Σ12 ![]() m , Σ11.2), unde Σ11.2
= Σ11- Σ12
m , Σ11.2), unde Σ11.2
= Σ11- Σ12 ![]() Σ21.
Σ21.
Pentru a calcula inversa matricei Σ22=![]() , putem folosi rezultatele teoretice pentru o matrice
diagonala sau putem proceda clasic, adica:
, putem folosi rezultatele teoretice pentru o matrice
diagonala sau putem proceda clasic, adica:
=![]() => det(Σ22)
= 4 si (Σ22)t = Σ22, matricea
adjuncta este (Σ22)*=
=> det(Σ22)
= 4 si (Σ22)t = Σ22, matricea
adjuncta este (Σ22)*=![]() si deci inversa este (Σ22)-1 =
si deci inversa este (Σ22)-1 = ![]() ·(Σ22)*=
·(Σ22)*=
![]()
![]() =
=![]() .
.
Asadar,
![]() m - Σ12
m - Σ12 ![]() m
m ![]() /2)
/2)![]()
![]() = 1 - (1/4
= 1 - (1/4 ![]() /4)
/4)![]() =
=
![]() = 1 - 1/2 + 3
= 1 - 1/2 + 3![]() /4= 1/2 + 3
/4= 1/2 + 3![]() /4, iar
/4, iar
= Σ11 - Σ12
![]() Σ21 = 2 - (1/2
Σ21 = 2 - (1/2 ![]() /2)
/2)![]()
![]() = 2 - (1/4
= 2 - (1/4 ![]() /2)
/2)![]() =
=
=2 - 1/8 - 3/8 = 2 - 1/2 = 3/2
=> X(1)
= X2 ~ N(1/2 + 3![]() /4, 3/2)
/4, 3/2)
Reamintim ca pentru o variabila normala unidimensionala N(m,σ2) functia de densitate are forma
f(x) = 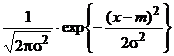
Aici avem m = 1/2 + 3![]() /4 si σ2 =3/2 si astfel f(x)
=
/4 si σ2 =3/2 si astfel f(x)
= 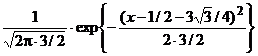 => => fX (x) =
=> => fX (x) =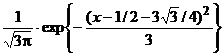 .
.
Pentru calculul functiei de densitate pentru
cea de-a doua componenta, X(2)
=![]() ~ N m , Σ22), unde m =
~ N m , Σ22), unde m =![]() si Σ22
=
si Σ22
=![]() , reamintim ca functia de densitate pentru un vector normal
, reamintim ca functia de densitate pentru un vector normal
N(m n-dimensional are forma
f(x)
= 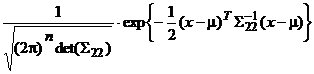
unde x este un vector n-dimensional. Inlocuind, se obtine (n=2)
f(x1,
x3) = 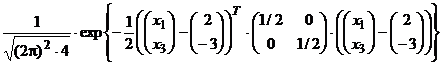 =
=
=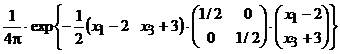 = =
= =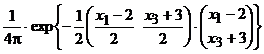 =
= 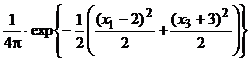 =>
=>
Deci, functia de densitate a vectorului ![]() este f(x1, x3) =
este f(x1, x3) = 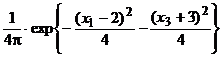
b) sa se determine
functia de regresie a lui X1
in raport cu ![]()
Reamintim ca functia de regresie a lui X(1) in raport cu X(2) este
M[X(1) / X(2)= x(2)] = m + Σ12 ![]() (x(2)-m
(x(2)-m
In cazul nostru, X(1) = X1,
X(2) =![]() si cum m =
si cum m = ![]() , Σ =
, Σ =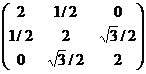 rezulta ca
rezulta ca
m = (liniile din m conform X(1) = X1, adica a prima linie) = 2
m = (liniile din m conform X(2) = ![]() , adica linia 2 si 3) =
, adica linia 2 si 3) = ![]()
= (liniile din Σ conform X(1) = X1 si coloanele tot conform X(1) = X1, adica linia 1 si coloana 1) = 2
= (liniile din Σ conform X(1) = X1
si coloanele conform X(2) =
![]() , adica linia 1 si coloanele 2 si 3) =
(1/2 0)
, adica linia 1 si coloanele 2 si 3) =
(1/2 0)
= (liniile din Σ conform X(2) = ![]() si coloanele
conform X(1) = X1, adica liniile 2
si 3 si coloana 1) =
si coloanele
conform X(1) = X1, adica liniile 2
si 3 si coloana 1) = ![]()
= (liniile din Σ conform X(2) = ![]() si coloanele tot
conform X(2) =
si coloanele tot
conform X(2) =![]() , adica liniile 2 si 3 si coloanele 2 si
3) =
, adica liniile 2 si 3 si coloanele 2 si
3) = 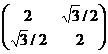 .
.
Pentru a calcula ![]() : Σ22
=
: Σ22
=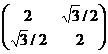 => (Σ22)*
=
=> (Σ22)*
=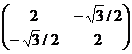 si cum
si cum
det (Σ22) =13
/ 4 rezulta ca ![]() =
=![]() (Σ22)*
=
(Σ22)*
=![]()
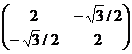 . Astfel:
. Astfel:
M[X(1)
/ X(2)= x(2)] = M[X1 / 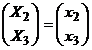 m + Σ12
m + Σ12 ![]() (x(2)-m ) =
(x(2)-m ) =
= 2 + (1/2 0)·![]()
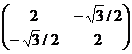 ·
·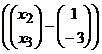 = 2 + (4/13 -
= 2 + (4/13 -![]() /13)·
/13)· 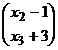 =
=
= 2 + 4(x2-1)/13 - ![]() (x3+3)/13 = (22-3
(x3+3)/13 = (22-3![]() )/13 + 4x2 / 13 -
)/13 + 4x2 / 13 - ![]() x3 / 13.
x3 / 13.
=> M[X1 / 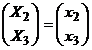 ] = (22-3
] = (22-3![]() )/13 + 4x2 / 13 -
)/13 + 4x2 / 13 - ![]() x3 / 13
x3 / 13
c) sa se determine
functia de regresie a lui ![]() in raport cu X1
in raport cu X1
Functia de regresie a lui X(1) in raport cu X(2) este M[X(1)
/ X(2)= x(2)] = m + Σ12 ![]() (x(2)-m
(x(2)-m
doar ca X(1)=![]() , X(2)=X1 (invers fata de
punctul b) si cum m=
, X(2)=X1 (invers fata de
punctul b) si cum m=![]() , Σ=
, Σ=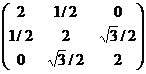 rezulta ca
rezulta ca
m = (liniile din m conform X(1) = ![]() , adica linia 2 si 3) =
, adica linia 2 si 3) = ![]()
m = (liniile din m conform X(2) = X1, adica a prima linie) = 2
= (liniile din Σ conform X(1) si
coloanele tot conform X(1) ,
adica liniile 2 si 3 si coloanele 2 si 3) = 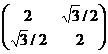 .
.
=(liniile din Σ conform X(1) si coloanele conform X(2) , adica liniile 2 si 3 si coloana
1)=![]()
= (liniile din Σ conform X(2) = X1 si coloanele conform X(1) , adica linia 1 si coloanele 2 si 3) = (1/2 0)
=(liniile din Σ conform X(2)=X1 si coloanele tot conform X(2)=X2, adica linia 1 si coloana 1) =2
Pentru a calcula ![]() , cum Σ22 este o
matrice de ordinul 1 atunci invesa sa este 1/elementul matricei =>
, cum Σ22 este o
matrice de ordinul 1 atunci invesa sa este 1/elementul matricei => ![]() = 1 / 2. Astfel:
= 1 / 2. Astfel:
M[X(1)
/ X(2)= x(2)] = M[![]() / X1= x1] = m + Σ12
/ X1= x1] = m + Σ12 ![]() (x(2)-m ) =
(x(2)-m ) =
= ![]() +
+ ![]() ·
·![]() ( x1-2)=
( x1-2)=
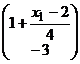 => M[
=> M[![]() / X1= x1] =
/ X1= x1] =![]() .
.
De aici se pot obtine si functiile de regresie ale variabilelor X2, respectiv X3 in raport cu X1
M[X2 / X1= x1] = (x1 + 1) / 4.
M[X3 / X1= x1] = -3.
Si de exemplu, daca
s-ar cere functia de regresie a variabilei X2 in raport
cu X3 se poate determina functia de regresie a
vectorului ![]() in raport cu X3. (tema)
in raport cu X3. (tema)
Exercitiu pentru acasa: Determinati functia de regresie a lui X1 in raport cu X3 si functia de regresie a lui X3 in raport cu X2.
Exercitiu pentru acasa: Fie X =![]() ~ N m, Σ) , unde m =
~ N m, Σ) , unde m = ![]() , Σ =
, Σ =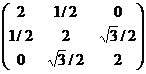
a) sa se determine functiile de densitate ale repartitiilor marginale corespunzatoare variabilelor X1 si X3.
b) sa se determine functia de regresie a variabilei X1 asupra variabilei X3.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Conversia la o locatie de alte dimensiuni |
| Functii diferentiabile |
| APLICAII LINIARE |
| FORMULE |
| Spatiu vectorial |
| Functia de gradul al II-lea |
| Definitia geometrica si cea axiomatica |
| SPATII VECTORIALE |
| Termeni si conditii |
| Contact |
| Creeaza si tu |