SPATII VECTORIALE
Legi de compozitie.
Definitia 1. Daca X este o multime
nevida, atunci orice aplicatie ![]() se numeste lege
de compozitie interna.
se numeste lege
de compozitie interna.
Observatia 1.
Legea de compozitie fiind o
functie, rezulta ca perechii ![]() iI corespunde in mod
unic un element
iI corespunde in mod
unic un element ![]() si scriem aceasta
astfel:
si scriem aceasta
astfel: ![]()
Uzual, aplicatia f privita ca
lege de compozitie se noteaza cu:![]() etc.
etc.
Daca f se noteaza cu "+", spunem ca legea de compozitie este notata aditiv.
Daca f se noteaza cu ".", spunem ca legea este notata multiplicativ.
Definitia 2. Fie K o multime nevida,
numita multime de operatori. Atunci, orice aplicatie ![]() se numeste lege
de compozitie externa pe X, cu operatori din K
se numeste lege
de compozitie externa pe X, cu operatori din K
Observatia 2. Uzual, legea de compozitie se noteaza cu ".".
Definitia 3. O multime dotata cu una sau mai multe legi de compozitie, interne sau externe, se numeste structura algebrica.
Definitia 4. Cuplul de obiecte matematice ![]() se numeste grup,
daca satisface urmatoarele axiome:
se numeste grup,
daca satisface urmatoarele axiome:
g1) ![]() (axioma
asociativitatii)
(axioma
asociativitatii)
g2) ![]() ( existenta
elementului neutru)
( existenta
elementului neutru)
g3) ![]() si x' se
numeste element neutru.
si x' se
numeste element neutru.
G4) Daca ![]() , grupul se numeste abelian, sau comutativ.
, grupul se numeste abelian, sau comutativ.
Definitia 5. Tripletul de obiecte matematice ![]() , unde
, unde
![]()
se numeste corp, daca sunt indeplinite axiomele:
k1) ![]() este grup abelian
este grup abelian
k2) ![]() este grup, unde 0 este
elementul neutru fata de adunarea in K
este grup, unde 0 este
elementul neutru fata de adunarea in K
k3) ![]() .
.
K4) Daca ![]() este grup abelian,
atunci K se numeste corp comutativ (camp).
este grup abelian,
atunci K se numeste corp comutativ (camp).
Observatia 3.
Grupul este o structura algebrica dotata cu o singura lege de compozitie interna.
Corpul este o structura algebrica dotata cu doua legi de compozitie interne.
Corpul numerelor reale sau complexe sunt campuri fata de operatiile cunoscute de adunare si de inmultire cu un scalar, real sau complex.
In continuare, prin camp vom intelege doar corpul de numere reale sau complexe, specificand de fiecare data despre care este vorba.
Spatii vectoriale. Definitie, proprietati.
Spatiul vectorial este o notiune care sta la baza multor capitole ale matematicii si care a fost definita prima oara de matematicianul Peano, in 1888. Se constituie ca o structura algebrica caracterizata de doua legi de compozitie, o lege interna si alta externa.
Fie X o multime nevida si fie operatiile:
![]() , operatie interna
, operatie interna
![]() , operatie externa.
, operatie externa.
Multimea K este un camp nevid, R sau C. Mai consideram, de asemenea, ca 0 este elementul neutru din K fata de adunarea numerelor si 1 este elementul neutru fata de inmultire.
Cvartetul ![]() il numim spatiu vectorial (spatiu liniar) daca
sunt indeplinite urmatoarele axiome:
il numim spatiu vectorial (spatiu liniar) daca
sunt indeplinite urmatoarele axiome:
v1) ![]()
v2) ![]()
v3) ![]()
v4) ![]()
v5) ![]()
v6) ![]()
Precizari:
Elementele lui X se numesc vectori si se noteaza cu x, y, z etc.
Elementele lui K se numesc
scalari si se noteaza cu ![]() etc.
etc.
Legea de compozitie interna notata cu "+" se numeste adunarea vectorilor.
Legea de compozitie externa notata cu " . " se numeste inmultirea unui vector cu un scalar, real sau complex, dupa cum K= R sau K= C.
![]() se numeste vectorul nul.
se numeste vectorul nul.
Adunarea scalarilor a fost notata, pentru simplificare, tot cu "+". Din context, insa, se va vedea de fiecare data despre care tip de adunare este vorba.
Analog, inmultirea scalarilor a fost notata tot cu ".".
Pentru simplificarea scrierii, prin notatia X s.v. K vom intelege spatiul vectorial X peste campul K.
ProprietatI:
Fie X s.v. K, unde K=R sau
K= C. Fie ![]() . Avem urmatoarele proprietatI:
. Avem urmatoarele proprietatI:
P1) ![]() .
.
P2) ![]() .
.
P3) ![]() unice.
unice.
P4) ![]()
P5) ![]()
Se observa ca din axioma v1) si din proprietatile 1,2,4 rezulta ca X este grup abelian in raport cu adunarea vectorilor. Prin urmare, orice spatiu vectorial este grup abelian fata de adunarea vectorilor.
Subspatiu al unui spatiu vectorial
Definitia 2. O submultime ![]() a unui spatiu vectorial X peste K se numeste
subspatiu vectorial, daca:
a unui spatiu vectorial X peste K se numeste
subspatiu vectorial, daca:
![]()
Fie ![]()
![]() , doua subspatii vectoriale ale lui X.
, doua subspatii vectoriale ale lui X.
Definitia 3. Multimea de mai jos se
numeste suma subspatiilor date si se noteaza cu ![]() .
.
![]()
Teorema 1. ![]() ssp. X (subspatiu
vectorial al lui X)
ssp. X (subspatiu
vectorial al lui X)
Precizare: In general, perechea ![]() nu este unica,
astfel ca x = y +z.
nu este unica,
astfel ca x = y +z. ![]() este cel mai mic
subspatiu care include pe
este cel mai mic
subspatiu care include pe ![]() .
.
Dependenta si independenta liniara.
Fie X s.v.K , unde K=R sau
K=C. Fie ![]() o submultime a
lui X.
o submultime a
lui X.
Definitia 4. Vectorii ![]() se numesc liniar
dependenti daca exista scalarii
se numesc liniar
dependenti daca exista scalarii 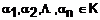 , nu toti nuli, astfel ca
, nu toti nuli, astfel ca ![]() .
.
Definitia 5. Vectorii ![]() se numesc liniar
independenti daca nu sunt liniar dependenti. Cu alte cuvinte,
vectorii
se numesc liniar
independenti daca nu sunt liniar dependenti. Cu alte cuvinte,
vectorii ![]() se numesc liniar
independenti daca din orice combinatie liniara de forma
se numesc liniar
independenti daca din orice combinatie liniara de forma ![]() , rezulta ca scalarii
, rezulta ca scalarii 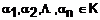 sunt toti nuli.
sunt toti nuli.
Observatia 4. Daca privim determinantul sistemului de la exercitiul de mai sus, observam ca el este format cu vectorii dati in ipoteza asezati pe coloane. din aceasta observatie, fara a mai trece prin algoritmul de calcul care conduce la concluzie ( si care face obiectul seminarului), stabilim ca daca numarul de vectori dintr-un sistem este egal cu numarul de componente ale unui vector, atunci ei sunt liniar independenti daca putem construi cu ajutorul lor un determinant diferit de 0. Altfel, daca determinantul obtinut este 0, spunem ca vectorii sunt liniar dependenti.
Observatia 5. Notiunile de liniar dependenta si independenta au fost definite pentru o multime S de vectori, multime care are (vezi def 5. si mai sus) un numar finit de elemente. Definitia poate fi extinsa pentru urice tip de submultime a lui X s.v.K, dupa cum urmeaza:
Definitia 6. Fie M o submultime nevida a lui X s.v.K. Spunem ca M este liniar dependenta daca exista cel putin o submultime finita a sa liniar dependenta si liniar independenta daca orice submultime finita a sa este liniar independenta.
ProprietatI:
Daca X s.v.K, atunci:
P1) Un vector ![]() s.v.K este liniar
dependent ddaca este vectorul nul.
s.v.K este liniar
dependent ddaca este vectorul nul.
P2) Orice vector nenul din X s.v.K este liniar independent.
P3) Daca o parte a unui sistem de vectori este liniar dependenta, atunci intregul sistem este liniar dependent.
P4) Orice sistem de vectori care contine vectorul nul este liniar dependent.
P5) Daca avem un sistem de vectori liniar dependent, atunci orice vector din acest sistem se poate scrie ca o combinatie liniara de ceilalti vectori.
Baza si dimensiune. Coordonate.
Fie B o submultime nevida a lui X s.v.K, finita sau nu.
Definitia 7. Multimea B se numeste baza (baza algebrica) daca sunt indeplinite urmatoarele conditii:
b1) B este liniar independenta.
b2) B este sistem de generatori, adica:
![]() .
.
Observatia 6. Utilizand un aparat matematic complex din teoria multimilor, se poate arata ca in orice spatiu vectorial exista cel putin o baza. Numarul elementelor dintr-o baza poate fi infinit sau finit si il vom nota cu card B.
Teorema 2. Un spatiu vectorial poate sa aiba mai multe baze, dar acestea au intotdeauna acelasi cardinal.
Definitia 8. Spatiul vectorial X peste K se
numeste finit dimensional daca ![]() sau daca, B fiind
o baza a sa, avem card B <
sau daca, B fiind
o baza a sa, avem card B <![]() .
.
Definitia 9. Dimensiunea unui spatiu vectorial se noteaza si se exprima astfel:
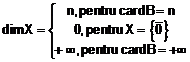
Observatia 7. Spatiile finit dimensionale se
vor nota in continuare cu ![]() si vom spune
ca au dimensiunea n. Evident, o baza intr-un astfel de spatiu
are n elemente si o vom nota cu
si vom spune
ca au dimensiunea n. Evident, o baza intr-un astfel de spatiu
are n elemente si o vom nota cu ![]() .
.
Teorema 3. Daca ![]() este s.v.K si
este s.v.K si ![]() este o baza in
acest spatiu, atunci pentru orice vector x din X, exista si sunt
unici scalarii
este o baza in
acest spatiu, atunci pentru orice vector x din X, exista si sunt
unici scalarii ![]() K astfel ca
K astfel ca ![]() .
.
Definitia 9. Scalarii ![]() se numesc coordonatele
lui x in baza B.
se numesc coordonatele
lui x in baza B.
Precizari:
Uzual, coordonatele ![]() de mai sus se
noteaza cu
de mai sus se
noteaza cu ![]() . Aceasta notatie este utilizata datorita
unui izomorfism care se poate stabili intre orice spatiu de dimensiune n si
spatiul aritmetic
. Aceasta notatie este utilizata datorita
unui izomorfism care se poate stabili intre orice spatiu de dimensiune n si
spatiul aritmetic ![]() . ?n continuare, prin notatia
. ?n continuare, prin notatia ![]() vom intelege
vectorul x de coordonate
vom intelege
vectorul x de coordonate ![]() .
.
Teorema 4. Daca ![]() este s.v.K de dimensiune n,
este s.v.K de dimensiune n, ![]() sunt m vectori ai
spatiului, cu care construim o matrice A cu coloanele formate cu vectorii dati
asezati pe coloane, spunem ca vectorii
sunt m vectori ai
spatiului, cu care construim o matrice A cu coloanele formate cu vectorii dati
asezati pe coloane, spunem ca vectorii ![]() sunt liniar
independenti
sunt liniar
independenti ![]() .
.
Teorema 5. Daca ![]() s.v.K , atunci oricare
n+1 vectori ai spatiului dat sunt liniar dependenti.
s.v.K , atunci oricare
n+1 vectori ai spatiului dat sunt liniar dependenti.
Teorema 6. Daca ![]() s.v.K , atunci un
sistem format din n vectori formeaza baza pentru spatiul dat
ddaca este liniar independent.
s.v.K , atunci un
sistem format din n vectori formeaza baza pentru spatiul dat
ddaca este liniar independent.
Observatia 8. Asadar, pentru un spatiu vectorial de dimensiune finita, notiunile de baza si liniar independenta sunt echivalente pentru o multime de vectori cu cardinalul egal cu dimensiunea spatiului. (Teorema lui Steinitz).
Daca ![]() sunt sistem de
generatori pentru un spatiu vectorial X, notam
sunt sistem de
generatori pentru un spatiu vectorial X, notam
![]()
Trecerea unui vector dintr-o baza in alta.
Fie ![]() s.v. K si fie
doua baze diferite ale acestui spatiu, pe care le notam cu:
s.v. K si fie
doua baze diferite ale acestui spatiu, pe care le notam cu:
![]()
Presupunem ca se
cunosc coordonatele unui vector dat ![]() in raport cu baza B,
pe care le notam cu
in raport cu baza B,
pe care le notam cu ![]() . Punem problema determinarii coordonatelor lui x in
baza B', pornind de la elementele cunoscute.
. Punem problema determinarii coordonatelor lui x in
baza B', pornind de la elementele cunoscute.
Consideram scrierea lui x in raport cu cele doua baze:
![]()
Scalarii ![]() sunt coordonatele lui
x in baza B' si urmeaza a fi determinati.
sunt coordonatele lui
x in baza B' si urmeaza a fi determinati.
Problema se va rezolva in doua etape:
I. Exprimarea vectorilor bazei B' in functie de vectorii din baza B.
II. Exprimarea coordonatelor vectorului x in raport cu baza B' fata de coordonatele cunoscute ale lui x in baza B, utilizand elementele stabilite la I.
I. Din faptul ca B este baza a lui X, rezulta ca orice vector din x se poate scrie in functie de elementele din B astfel:
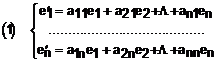
Notam:
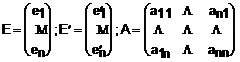 .
.
Relatia (1) se va
scrie in forma matriceala:![]() , relatie care stabileste legatura dintre cele
doua baze.
, relatie care stabileste legatura dintre cele
doua baze.
Matricea A se numeste matricea de trecere de la baza B la baza B'.
II. Exprimarea coordonatelor lui x in raport cu baza B'.
Avem scrierile:
![]()
Din (1), se observa
ca putem inlocui pe ![]() in functie de
in functie de ![]() si de elementele
matricii A, deci:
si de elementele
matricii A, deci:
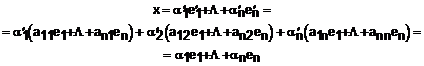
Urmarea efectuarii calculelor si a identificarii coeficientilor intre vectorii bazei B, rezulta:
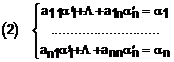 .
.
Sistemul se rezolva
prin metoda Cramer si tinand cont ca detA este nenul,
solutia ![]() va fi unica.
va fi unica.
Notam:
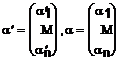 .
.
Sistemul (2) se va scrie in forma matriceala:
![]() .
.
Deoarece A este
nesingulara, determinam ![]() , relatie care exprima legatura dintre
coordonatele lui x scris in baza B', cu coordonatele (cunoscute) ale lui x
scris in baza B.
, relatie care exprima legatura dintre
coordonatele lui x scris in baza B', cu coordonatele (cunoscute) ale lui x
scris in baza B.
Produs scalar. Spatii euclidiene. Proprietati. Exemple.
Fie X s.v.K, unde K= R sau K= C.
Definitia 10. Aplicatia ![]() se numeste produs
scalar, daca sunt indeplinite urmatoarele axiome:
se numeste produs
scalar, daca sunt indeplinite urmatoarele axiome:
p1) ![]()
p2) ![]()
p3) ![]() .
.
ProprietatI:
P1) ![]()
P2) ![]() .
.
Pentru doi vectori arbitrari din
spatiul ![]() , de forma
, de forma ![]() , se poate arata ca aplicatia
, se poate arata ca aplicatia ![]() , data de
, data de
![]() ,
,
este produs scalar. Aceasta aplicatie va fi utilizata in continuare pentru diverse aplicatii ale produsului scalar.
Definitia 11. Perechea ![]() se numeste
spatiu euclidian. Prin urmare, numim spatiu euclidian orice
spatiu vectorial dotat cu cel putin un produs scalar.
se numeste
spatiu euclidian. Prin urmare, numim spatiu euclidian orice
spatiu vectorial dotat cu cel putin un produs scalar.
Norma. Spatii normate.
Fie X s.v.K, unde K= R sau K= C.
Definitia 12. Aplicatia ![]() se numeste
norma pe X, daca sunt satisfacute urmatoarele axiome:
se numeste
norma pe X, daca sunt satisfacute urmatoarele axiome:
n1) ![]() . (inegalitatea triunghiului)
. (inegalitatea triunghiului)
n2) ![]() (axioma
omogenitatii)
(axioma
omogenitatii)
n3) Pentru ![]() .
.
Definitia 13. Cuplul de obiecte matematice ![]() se numeste
spatiu normat.
se numeste
spatiu normat.
ProprietatI:
P1) ![]()
P2) ![]() .
.
Teorema 7. Fiind dat un spatiu euclidian ![]() , expresia:
, expresia: ![]() defineste
intotdeauna o norma.
defineste
intotdeauna o norma.
Observatia 9. In spatiul euclidian ![]() , inafara de norma pe care am introdus-o in teorema 9.
mai exista si alte norme care nu mai provin, insa, dintr-un
produs scalar.
, inafara de norma pe care am introdus-o in teorema 9.
mai exista si alte norme care nu mai provin, insa, dintr-un
produs scalar.
Daca x este un element
al spatiului ![]() , cu coordonatele date de:
, cu coordonatele date de: ![]() , definim:
, definim:
![]()
![]()
Observatia 10. Are loc urmatoarea inegalitate:
![]() .
.
ProprietatI:
P1) Orice spatiu euclidian este spatiu normat, deoarece din teorema 9. rezulta ca putem defini o norma pornind de la un produs scalar.
P2) Nu intotdeauna un spatiu normat poate fi organizat ca spatiu euclidian, deoarece nu orice norma provine dintr-un produs scalar (vezi, de exemplu, norma unu).
Distanta. Spatii metrice. Proprietati.
Fie X o multime nevida.
Definitia 14. Aplicatia ![]() se numeste distanta
sau metrica pe X, daca sunt indeplinite urmatoarele axiome:
se numeste distanta
sau metrica pe X, daca sunt indeplinite urmatoarele axiome:
d1) ![]() .
.
D2) ![]()
d3) ![]()
Definitia 15. Cuplul de obiecte matematice ![]() se numeste
spatiu metric.
se numeste
spatiu metric.
ProprietatI:
P1) ![]()
P2) ![]() .
.
Teorema 10. Daca ![]() este un spatiu
normat, atunci aplicatia definita de
este un spatiu
normat, atunci aplicatia definita de ![]() este o metrica pe
X.
este o metrica pe
X.
Observatia 11. Din teorema de mai sus rezulta ca orice spatiu normat este spatiu metric si, din proprietatea P1) de la paragraful anterior rezulta ca orice spatiu euclidian este spatiu metric. Rezulta de asemenea, din P2), ca reciproca nu este adevarata.
Pe parcurs, vom mai introduce si alte elemente de teorie, pe masura ce va fi necesar.
EXEMPLE
1. Aratati ca structurile urmatoare sunt spatii vectoriale:
a) ![]()
b)![]() . Atunci,
. Atunci, ![]() este spatiu
vectorial real.
este spatiu
vectorial real.
c) ![]() spatiu vectorial
real.
spatiu vectorial
real.
d) ![]() spatiu vectorial real, unde
spatiu vectorial real, unde
![]() .
.
Solutie:
Rezolvarea problemei propuse presupune verificarea axiomelor de spatiu vectorial pe care le-am enuntat in elementele de teorie. Prezentam rezolvarea pentru punctul b), iar pentru usurarea scrierii prezentam cazul particular n= 2.
![]()
v1) ![]() .
.
Fie x,y,z de forma:
![]()
![]()
![]()
Egalitatea de demonstrat conduce la egalitatea polinoamelor scrise mai sus ceea ce inseamna, urmarea identificarii coeficientilor:
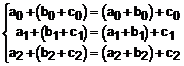
Aceste egalitati sunt in mod evident adevarate datorita asociativitatii adunarii numerelor reale.
V2) ![]() .
.
Aceasta a doua axioma de spatiu vectorial ne asigura de existenta elementului neutru fata de adunarea polinoamelor de grad cel mult 2. Fie, deci
![]() .
.
?n aceste conditii,
![]() .
.
Prin urmare, relatia
se verifica pentru ![]() definit ca mai sus.
definit ca mai sus.
V3) ![]() .
.
Relatia este evidenta:
![]() .
.
V4) ![]() .
.
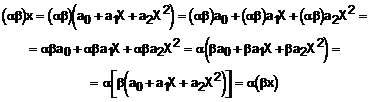
v5) ![]()
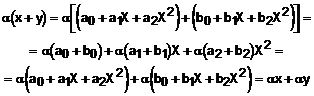
v6) ![]() .
.
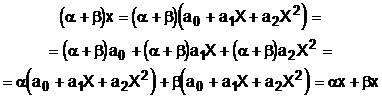
2. Aratati ca urmatoarele multimi reprezinta subspatii vectoriale ale spatiilor mentionate:
a) Sa se determine valorile parametrului real m pentru care
![]()
b) ![]() subspatiu al lui
subspatiu al lui ![]() .
.
c) ![]() este subspatiu vectorial al lui
este subspatiu vectorial al lui ![]() .
.
Solutie:
Definitia subspatiului vectorial, precizata in elementele de teorie este:
![]()
a) Fie ![]() multimea despre care urmeaza sa
demonstram ca este subspatiu vectorial al lui
multimea despre care urmeaza sa
demonstram ca este subspatiu vectorial al lui ![]() . Pentru aceasta vom considera doua elemente ale acestei
multimi, pe care le vom nota (vezi forma lui W) cu
. Pentru aceasta vom considera doua elemente ale acestei
multimi, pe care le vom nota (vezi forma lui W) cu ![]() , unde coordonatele acestor doi vectori satisfac
conditia din definitia lui W:
, unde coordonatele acestor doi vectori satisfac
conditia din definitia lui W:
![]()
Pentru a dovedi ca W
este subspatiu vectorial, consideram combinatia liniara ![]() si
demonstram ca este element al lui W,
si
demonstram ca este element al lui W, ![]() .
.
![]()
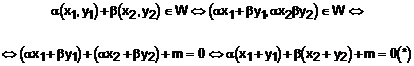
Pe de alta parte, ![]()
![]() .
.
Inlocuim in (*) si avem:
![]()
d) Fie ![]() . Evaluam suma
. Evaluam suma ![]() , unde:
, unde:
![]() .
.
Evident, ![]()
![]() . Calculam
. Calculam
![]()
Prin urmare, ![]() , deci definitia subspatiului vectorial este
verificata.
, deci definitia subspatiului vectorial este
verificata.
3. Stabiliti daca vectorii de mai jos sunt liniar independenti, iar in caz contrar stabiliti relatia de dependenta:
a) ![]() .
.
b) ![]()
c) ![]()
d) ![]() .
.
e) ![]()
Solutie:
a) Evident, acesti 3
vectori sunt din ![]() , deoarece au 3 componente. Sa stabilim, utilizand
definitia, daca ei sunt liniar independenti. Pentru aceasta, vom
considera o combinatie liniara de forma:
, deoarece au 3 componente. Sa stabilim, utilizand
definitia, daca ei sunt liniar independenti. Pentru aceasta, vom
considera o combinatie liniara de forma:
![]()
Determinam valorile
lui![]() . Inlocuim vectorii care ni s-au dat:
. Inlocuim vectorii care ni s-au dat:
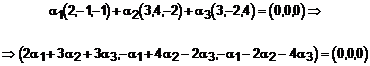
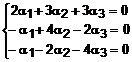
Problema s-a redus, asadar la rezolvarea unui sistem de trei ecuatii cu trei necunoscute, in care termenul liber este egal cu 0. Calculam determinantul sistemului:
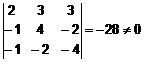
Atunci, sistemul are solutie unica si in plus, deoarece termenul liber este nul, aceasta unica solutie este nula:
![]()
Concluzionam de aici
ca ne incadram in definitia sistemului liniar independent, deci ![]() sunt liniar independenti.
sunt liniar independenti.
Observatia 12. Problema deciderii daca un sistem de vectori este sau nu liniar independent s-a redus, dupa cum am vazut, la calculul unui determinant. Ca metoda de lucru pentru astfel de probleme, propunem urmatoarele:
Dorim sa aflam
daca vectorii ![]() sunt liniar
independenti, unde
sunt liniar
independenti, unde ![]() . Construim cu ajutorul acestor n vectori, asezati
pe coloana, un determinant de ordinul n si il calculam.
. Construim cu ajutorul acestor n vectori, asezati
pe coloana, un determinant de ordinul n si il calculam.
n daca det = 0, vectorii sunt liniar dependenti
n
daca det![]() 0, vectorii sunt liniar independenti.
0, vectorii sunt liniar independenti.
Aceasta metoda se poate aplica doar pentru sisteme de vectori pentru care numarul vectorilor din sistem este egal cu numarul de componente. Pentru trei vectori de cate patru componente, de exemplu, putem construi matricea, dar nu mai are sens determinantul, deoarece matricea construita nu mai este patratica. Pentru sistemele de vectori care nu intra sub incidenta metodei, procedam astfel:
n Daca numarul de vectori din sistem este mai mare decat numarul de componente, elementele de teorie ne asigura ca ei nu pot fi liniar independenti.
n Daca numarul de
vectori din sistem este mai mic decat numarul de componente, putem utiliza
determinantul Gramm, care pentru un sistem format din vectorii ![]() se defineste astfel:
se defineste astfel:
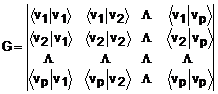
unde ![]() reprezinta
produsul scalar al vectorilor
reprezinta
produsul scalar al vectorilor ![]() . Regula pe care o vom aplica spune ca daca G este
nul, sistemul de vectori cu care a fost construit este liniar dependent, iar
daca este nenul, vectorii sunt liniar independenti. Vom aplica
aceasta metoda pentru exercitiul de la g).
. Regula pe care o vom aplica spune ca daca G este
nul, sistemul de vectori cu care a fost construit este liniar dependent, iar
daca este nenul, vectorii sunt liniar independenti. Vom aplica
aceasta metoda pentru exercitiul de la g).
d) Pentru sistemul de vectori dat, verificam liniar dependenta sau independenta construind determinantul despre care am discutat:
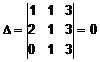 .
.
Prin urmare, vectorii dati sunt liniar dependenti. Pentru stabilirea relatiei de dependenta dintre ei, determinam coeficientii combinatiei liniare:
![]() .
.
Prin inlocuire si dupa efectuarea calculelor, rezulta urmatorul sistem de ecuatii algebrice liniare:
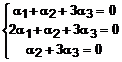 .
.
Determinantul acestui sistem este chiar determinantul calculat mai sus, deci sistemul este compatibil (fiind sistem omogen) si nedeterminat. Fie minorul nenul de ordinul al doilea
![]()
care corespunde primelor doua ecuatii din sistem si necunoscutelor
![]() . Mentinem, deci, aceste doua ecuatii, iar
necunoscuta
. Mentinem, deci, aceste doua ecuatii, iar
necunoscuta ![]() o presupunem
egala cu un numar real arbitrar, t.
o presupunem
egala cu un numar real arbitrar, t.
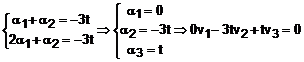
Pentru ca t este real arbitrar, fie t=1, deci relatia de dependenta devine:
![]() .
.
e) Verificam liniar dependenta celor trei polinoame date:
Fie, deci, combinatia liniara:
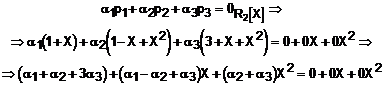
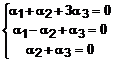
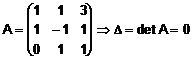
Prin urmare, sistemul de vectori este liniar dependent. Determinam relatia de dependenta rezolvand sistemul de mai sus. Solutia care rezulta este:
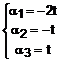 .
.
Deci, pentru t = 1, relatia de dependenta este:
![]() .
.
Ultima egalitate ne spune
ca polinomul ![]() apartine
spatiului vectorial generat de polinoamele
apartine
spatiului vectorial generat de polinoamele ![]() , fapt care se scrie:
, fapt care se scrie:
![]() .
.
f) Sistemul de vectori din
enunt este format din 3 vectori din ![]() , deci ne situam in conditiile constructiei
determinantului Gramm:
, deci ne situam in conditiile constructiei
determinantului Gramm:
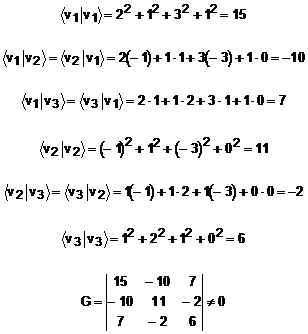
Prin urmare, sistemul de vectori din enunt este liniar independent.
4. Fie multimile definite prin:
![]()
![]()
Stabiliti daca ![]() sunt liniar
independenti. ?n caz contrar, determinati o submultime a lui
sunt liniar
independenti. ?n caz contrar, determinati o submultime a lui ![]() care este liniar
independenta sI care genereaza de asemenea spatiul
care este liniar
independenta sI care genereaza de asemenea spatiul ![]() . Aceeasi problema pentru spatiul
. Aceeasi problema pentru spatiul ![]() .
.
Solutie:
Verificam liniar
independenta sistemului de vectori ![]() utilizand
definitia:
utilizand
definitia:
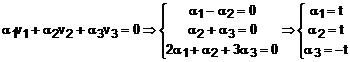
Prin urmare, relatia de dependenta este:
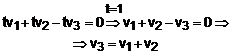
Deci, ![]() . Asa cum a fost definit, ca fiind generat de vectorii
. Asa cum a fost definit, ca fiind generat de vectorii ![]() , spatiul
, spatiul ![]() admite scrierea:
admite scrierea:
![]() .
.
Pe de alt a parte, ![]() , deci:
, deci:
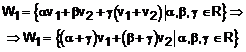
Urmarea unei notatii evidente, avem:
![]()
Sa dovedim ca
vectorii ![]() sunt liniar independenti:
sunt liniar independenti:
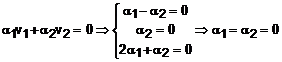
Prin urmare, vectorii ![]() sunt liniar
independenti si genereaza in acelasi timp spatiul
sunt liniar
independenti si genereaza in acelasi timp spatiul ![]() , deci reprezinta baza in
, deci reprezinta baza in ![]() .
.
6. Gasiti matricea de trecere de la baza B la baza B' si coordonatele vectorului v in fiecare din cazurile de mai jos:
a) ![]()
![]()
b) ![]()
![]()
Solutie:
a) Verificam daca sistemele de vectori date in ipoteza reprezinta baze in spatiul vectorial din care fac parte:
Pentru baza B: construim matricea A, formata cu vectorii asezati pe coloane:
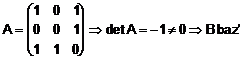 .
.
Pentru baza B': construim matricea A', formata cu vectorii asezati pe coloane:
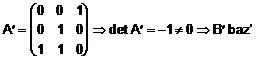 .
.
Pentru exprimarea matricii
de trecere de la baza B la baza B', trebuie sa determinam
coordonatele fiecarui vector al bazei B' in functie de vectorii bazei
B. Vom tine cont, pentru aceasta,
de faptul ca fiecare element al multimii B' este vector al spatiului
![]() , pentru care B este o baza, deci fiecare element al lui
B' se scrie in functie de elementele lui B dupa cum urmeaza:
, pentru care B este o baza, deci fiecare element al lui
B' se scrie in functie de elementele lui B dupa cum urmeaza:
Pentru vectorul ![]() :
:
![]()
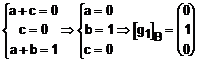
Exprimam vectorul ![]()
![]()
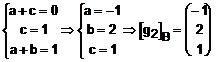
Exprimam vectorul ![]() :
:
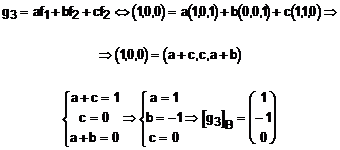
Matricea de trecere de la baza B la baza B' este formata cu vectorii determinati mai sus asezati pe coloane, (adica asa cum I-am scris):
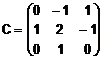
Coordonatele lui v = (2, 1, 3 ) in baza B sunt date de egalitatea de mai jos:
![]()
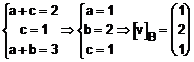
Va propunem sa determinati coordonatele vectorului v in cealalta baza, B'.
b) Pentru spatiul ![]() , cunoastem baza
, cunoastem baza ![]() , deci orice polinom
, deci orice polinom ![]() admite scrierea
admite scrierea ![]() . Sa verificam daca sistemul de vectori B dat
in ipoteza este baza in
. Sa verificam daca sistemul de vectori B dat
in ipoteza este baza in ![]() :
:
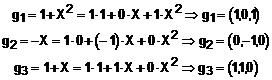
Construim matricea care are acesti 3 vectori scrisi pe coloane:
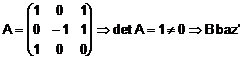 .
.
Analog pentru baza B':
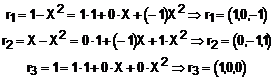
Construim matricea A' cu vectorii asezati pe coloane:
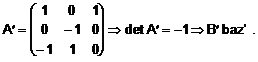
Cautam matricea de trecere de la baza B la baza B': aceasta inseamna o relatie intre matricea A sI matricea A': exprimam vectorii bazei B' in functie de elementele lui B:
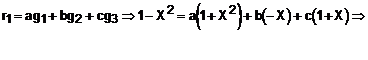
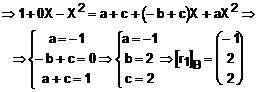
Exprimam vectorul ![]() :
: ![]()
Exprimam vectorul ![]() :
: ![]()
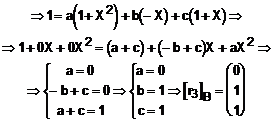
Matricea de trecere va fi 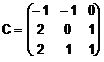
Ea este formata cu vectorii determinati mai sus asezati pe coloane.
Coordonatele vectorului ![]() in baza B le
determinam din relatia
in baza B le
determinam din relatia
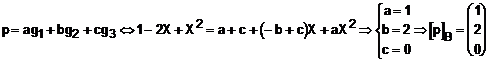
Va propunem ca tema exprimarea vectorului p in baza B'.
7. Completati sistemele de vectori de mai jos pana la o baza in spatiile vectoriale indicate:
a) ![]() .
.
b) ![]()
Solutie:
a) Sa verificam
liniar independenta vectorilor ![]() . Construim matricea A care are cei doi vectori
asezatI pe coloane. Liniar independenta lor presupune ca rangul
lui A sa fie egal cu 2:
. Construim matricea A care are cei doi vectori
asezatI pe coloane. Liniar independenta lor presupune ca rangul
lui A sa fie egal cu 2:
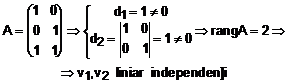
O baza in ![]() trebuie sa
aiba exact trei elemente, drept pentru care va trebui sa
completam sistemul de vectori dat in enunt cu inca un vector.
Mai mult, caracteristica unui sistem de vectori care formeaza o baza
in spatiul dat este aceea ca putem construi, cu ajutorul lor, o
matrice cu determinantul nenul. Cu alte cuvinte, vectorul care trebuie sa
completeze baza noastra il vom determina astfel ca sa completeze
matricea A pana la o matrice cu determinantul nenul. Exista o
infinitate de maniere de completare, dintre care dam ca exemplu matricea
trebuie sa
aiba exact trei elemente, drept pentru care va trebui sa
completam sistemul de vectori dat in enunt cu inca un vector.
Mai mult, caracteristica unui sistem de vectori care formeaza o baza
in spatiul dat este aceea ca putem construi, cu ajutorul lor, o
matrice cu determinantul nenul. Cu alte cuvinte, vectorul care trebuie sa
completeze baza noastra il vom determina astfel ca sa completeze
matricea A pana la o matrice cu determinantul nenul. Exista o
infinitate de maniere de completare, dintre care dam ca exemplu matricea
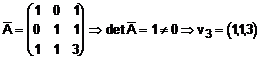
![]() este baza in
este baza in ![]() .
.
b) Verificam, pentru
inceput, liniar independenta vectorilor ![]() : consideram combinatia liniara:
: consideram combinatia liniara:
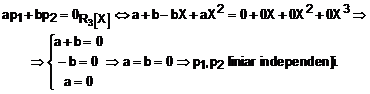
Exprimam vectorii din
ipoteza in functie de baza spatiului ![]() , data de
, data de
![]()
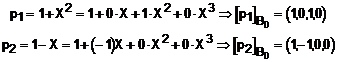
Formam matricea A cu
acesti doi vectori asezati pe coloana: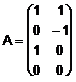
Deoarece baza ![]() are patru elemente,
inseamna ca orice alta baza a spatiului vectorial
are patru elemente,
inseamna ca orice alta baza a spatiului vectorial ![]() are tot 4 elemente. Prin urmare,
sistemului de vectori din ipoteza trebuie sa ii mai adaugam
2 vectori, fie ei
are tot 4 elemente. Prin urmare,
sistemului de vectori din ipoteza trebuie sa ii mai adaugam
2 vectori, fie ei ![]() , astfel ca multimea
, astfel ca multimea ![]() sa reprezinte baza a spatiului
sa reprezinte baza a spatiului ![]() .
.
Dar, din faptul ca
aceasta multime este baza, deducem ca determinantul format
cu cei 4 vectori asezati pe coloana trebuie sa fie nenul.
Prin urmare, daca vom completa matricea A pana la o matrice A', cu
doua coloane astfel ca determinantul matricii rezultate sa fie nenul,
acele doua coloane adaugate reprezinta doi vectori care
completeaza multimea din ipoteza pana la o baza in ![]() .
.
Fie, de exemplu, completarea:
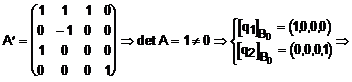
![]()
Sa mai facem
mentiunea ca aceasta completare a sistemului de vectori din
ipoteza pana la o baza a lui ![]() nu este unica.
Oricare alte doua coloane am fi adaugat matricii A pentru a
obtine A' puteau reprezenta vectori care completau sistemul, cu
conditia ca determinantul matricii obtinute, A', sa fie nenul.
nu este unica.
Oricare alte doua coloane am fi adaugat matricii A pentru a
obtine A' puteau reprezenta vectori care completau sistemul, cu
conditia ca determinantul matricii obtinute, A', sa fie nenul.
8. Stabiliti
daca urmatoarea operatie determina produs scalar pe
spatiul vectorial dat: ![]() .
.
Solutie:
Pentru a stabili ca o aplicatie este produs scalar, avem de verificat axiomele pe care le-am enuntat in cadrul elementelor de teorie de la inceputul capitolului.
![]()
1) ![]()
Fie ![]() . Utilizand operatia data in ipoteza, axioma
de demonstrat se scrie:
. Utilizand operatia data in ipoteza, axioma
de demonstrat se scrie:
![]()
Relatia de mai sus este in mod evident adevarata, deci prima axioma a produsului scalar se verifica.
2) ![]() .
.
Fie ![]() . Axioma 2 capata forma urmatoare:
. Axioma 2 capata forma urmatoare:
![]() ,
,
ceea ce este in mod evident adevarat.
3) ![]()
.Fie ![]() . Axioma 3 devine:
. Axioma 3 devine:
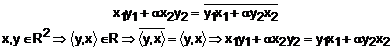
Deci, sI axioma 3 se verifica.
4) ![]() .
.
Fie ![]() . Axioma de verificat se scrie:
. Axioma de verificat se scrie: ![]()
Verificam ca ![]() .
. ![]() Prin urmare,
Prin urmare, ![]() .
.
Toate
proprietatile produsului scalar au fost verificate pentru valori
pozitive ale parametrului ![]() .
.
Definitia 16. Pentru doi vectori v si w, definim urmatoarele marimi:
n lungimea vectorului v: ![]()
n unghiul ![]() dintre vectorii v
si w:
dintre vectorii v
si w: ![]() , pentru situatia
in care produsul scalar este real pentru orice doi vectori ai spatiului
vectorial din care fac parte.
, pentru situatia
in care produsul scalar este real pentru orice doi vectori ai spatiului
vectorial din care fac parte.
n proiectia vectorului v
pe vectorul w: ![]()
9. Calculati
lungimea vectorilor dati mai jos si unghiul dintre ei, precum si
proiectia celui de-al doilea vector pe primul, utilizand produsul scalar
din problema anterioara, pentru ![]() :
:
![]()
Solutie:
Pentru vectorii din problema, produsul scalar este dat de
![]()
Deoarece vectorii au componente reale, putem determina unghiul dintre ei dupa formula data mai sus:
![]()
Proiectia celui de-al doilea vector pe primul este:
![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |