Siruri de functii
1. Fie ![]() un spatiu metric si
un spatiu metric si
![]() spatiul vectorial
real al functiilor definite pe
spatiul vectorial
real al functiilor definite pe ![]() cu valori reale. Vom
nota cu
cu valori reale. Vom
nota cu ![]() multimea functilor continue
multimea functilor continue ![]() . Cu operatiile obisnuite de adunare si
inmultire a functiilor, cat si inmultirea cu scalari a
functiilor, spatiul
. Cu operatiile obisnuite de adunare si
inmultire a functiilor, cat si inmultirea cu scalari a
functiilor, spatiul ![]() este o algebra de functii.
este o algebra de functii.
Pe spatiul ![]() definim norma convergrntei uniforme
definim norma convergrntei uniforme ![]() .
.
Cu aceasta norma ![]() devine o algebra
de functii normata deoarece, putem scrie
devine o algebra
de functii normata deoarece, putem scrie
![]() ,
, ![]() .
.
Daca ![]() este spatiu
metric compact atunci spatiul
este spatiu
metric compact atunci spatiul ![]() , cu norma introdusa mai sus, devine spatiu vectorial complet
(spatiu Banach).
, cu norma introdusa mai sus, devine spatiu vectorial complet
(spatiu Banach).
2. Observatie.
Pe spatiul ![]() se pot introduce
si alte norme fata de care acest spatiu nu este complet
(vezi seminarul).
se pot introduce
si alte norme fata de care acest spatiu nu este complet
(vezi seminarul).
3. Definitie. Se numeste sir de functii pe ![]() orice aplicatie
orice aplicatie ![]() care asociaza la
orice numar natural
care asociaza la
orice numar natural ![]() o functie
o functie ![]() definita pe
definita pe ![]() cu valori reale;
Asadar, putem scrie sirul de functii sub forma
cu valori reale;
Asadar, putem scrie sirul de functii sub forma ![]() sau sub forma
sau sub forma ![]() , in care caz observam ca toate functiile
, in care caz observam ca toate functiile ![]() ale sirului sunt
functii de aceeasi variabila
ale sirului sunt
functii de aceeasi variabila ![]() , sau scriind elementele sirului ca functii de
aceeasi variabila
, sau scriind elementele sirului ca functii de
aceeasi variabila ![]()
![]() . (1)
. (1)
Presupunem ca exista
puncte ![]() pentru care fiecare
sir numeric
pentru care fiecare
sir numeric ![]() este convergent
catre o limita finita. Deoarece limita sirului este
determinata de valoarea sirului in
este convergent
catre o limita finita. Deoarece limita sirului este
determinata de valoarea sirului in ![]() , este natural ca limita sa fie reprezentata
printr-o functie de variabila
, este natural ca limita sa fie reprezentata
printr-o functie de variabila ![]() .
.
Asadar, daca ![]() este un sir de
functii definite pe
este un sir de
functii definite pe ![]() cu valori reale
(eventual cu valori in
cu valori reale
(eventual cu valori in ![]() ) atunci
) atunci ![]() si
si ![]() sunt functii pe
sunt functii pe ![]() , definite prin
, definite prin
![]() si
si ![]() .
.
4. Definitie. Punctul ![]() , fixat, pentru care sirul numeric
, fixat, pentru care sirul numeric ![]() este convergent la
numarul real
este convergent la
numarul real ![]() se numeste punct de convergenta al
sirului numeric considerat.
se numeste punct de convergenta al
sirului numeric considerat.
Notam cu ![]() multimea
punctelor de convergenta ale sirului de functii
multimea
punctelor de convergenta ale sirului de functii ![]() din
din ![]()
Asadar, pentru fiecare ![]() fixat, sirul
numeric
fixat, sirul
numeric ![]() are limita. Asa
cum s-a precizat, limita sirului
este determinata de valoarea sirului in
are limita. Asa
cum s-a precizat, limita sirului
este determinata de valoarea sirului in ![]() . In consecinta, aceasta limita
reprezinta o functie
. In consecinta, aceasta limita
reprezinta o functie ![]() , de variabila
, de variabila ![]() , numita functia
limita si scriem
, numita functia
limita si scriem
![]() pentru orice
pentru orice ![]() . (2)
. (2)
In continuare vom analiza
existenta functiei limita pentru fiecare ![]() , cat si modul cum anumite proprietati
functionale ale sirurilor de functii se pot transmite sau nu functiei
limita.
, cat si modul cum anumite proprietati
functionale ale sirurilor de functii se pot transmite sau nu functiei
limita.
Exemple
Fie ![]() si sirul de
functii
si sirul de
functii ![]() ,
, ![]() , definit prin relatiile
, definit prin relatiile ![]() .
.
Observam ca ![]() . Multimea punctelor
de convergenta ale sirului
. Multimea punctelor
de convergenta ale sirului ![]() este
este ![]() . Functia
limita
. Functia
limita ![]() ,
, ![]() este definita
prin
este definita
prin
![]() .
.
Observam ca ![]() si deci,
proprietatea de continuitate a
sirului de functii nu este transmisa functiei limita (vezi, fig.1).
si deci,
proprietatea de continuitate a
sirului de functii nu este transmisa functiei limita (vezi, fig.1).
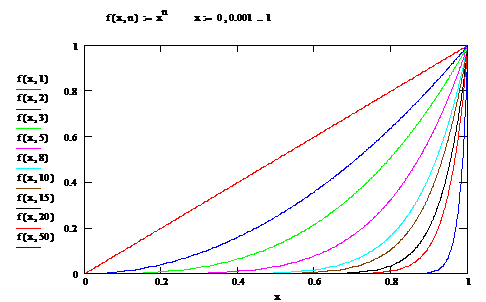
Figura
1. Graficele functiilor ![]() , pentru
, pentru ![]()
Fie ![]() si sirul de
functii
si sirul de
functii ![]() ,
, ![]() , definit prin relatiile
, definit prin relatiile ![]() . Observam ca
. Observam ca ![]() ,
, ![]() . Multimea punctelor
de convergenta ale sirului
. Multimea punctelor
de convergenta ale sirului ![]() este
este ![]() . Functia
limita
. Functia
limita ![]() ,
, ![]() este definita
prin
este definita
prin
![]() .
.
Observam ca ![]() si deci,
proprietatea de continuitate a
sirului de functii, prin trecere la limita, cand
si deci,
proprietatea de continuitate a
sirului de functii, prin trecere la limita, cand ![]() , se transmite functiei limita.
, se transmite functiei limita.
Figura
2. Graficele functiilor din exemplul (2), pentru valorile ![]() .
.
5. Definitie. Sirul de functii ![]() din
din ![]() se numeste punctual (simplu) convergent
catre functia
se numeste punctual (simplu) convergent
catre functia ![]() daca si
numai daca
daca si
numai daca
![]() ; si, in acest
caz, scriem
; si, in acest
caz, scriem ![]() .
.
Observatie. Definitia
afirma ca pentru orice ![]() sirul numeric
sirul numeric ![]() este convergent
catre limita finita (numarul real)
este convergent
catre limita finita (numarul real) ![]() .
.
Exercitiul
1. Fie ![]() un sir de
functii din
un sir de
functii din ![]() si
si ![]() . Afirmatiile urmatoare sunt echivalente:
. Afirmatiile urmatoare sunt echivalente:
(i). sirul ![]() este punctual
(simplu) convergent catre functia
este punctual
(simplu) convergent catre functia ![]() (
(![]() ).
).
(ii).
![]() si
si ![]() a.i. sa avem
a.i. sa avem ![]() pentru orice
pentru orice ![]() .
.
Echivalenta celor
doua afirmatii este evidenta. Intr-adevar, din
definitia limitei rezulta ca este suficient sa se ia o
valoare oarecare ![]() , dar fixata, pentru a avea sirul numeric
, dar fixata, pentru a avea sirul numeric ![]() convergent,
adica, pentru orice
convergent,
adica, pentru orice ![]() sa gasim
cate un numar
sa gasim
cate un numar ![]() a.i. pentru orice
a.i. pentru orice ![]() sa se verifice
inegalitatea
sa se verifice
inegalitatea ![]() in acel
in acel ![]() fixat. Daca se
alege alta valoare a lui
fixat. Daca se
alege alta valoare a lui ![]() , pentru acelasi
, pentru acelasi ![]() , numarul
, numarul ![]() poate sa nu fie
cel dinainte si atunci trebuie ales altul. Cum
poate sa nu fie
cel dinainte si atunci trebuie ales altul. Cum ![]() ia o infinitate de
valori, rezulta ca avem o infinitate de siruri numerice diferite
care converg catre o limita finita.
ia o infinitate de
valori, rezulta ca avem o infinitate de siruri numerice diferite
care converg catre o limita finita.
7. Definitie. Sirul de functii ![]() din
din ![]() se numeste uniform convergent pe
se numeste uniform convergent pe ![]() catre
functia
catre
functia ![]() si, notam
si, notam ![]() ), daca si numai daca
), daca si numai daca
![]() a.i. pentru orice
a.i. pentru orice ![]() si
si ![]() sa avem
sa avem ![]() .
.
8. Observatie. Definitia afirma ca pentru un ![]() dat, exista un
acelasi numar natural
dat, exista un
acelasi numar natural ![]() care corespunde pentru
toate sirurile numerice
care corespunde pentru
toate sirurile numerice ![]() cu
cu ![]() , care converg catre limita finita
, care converg catre limita finita ![]() .
.
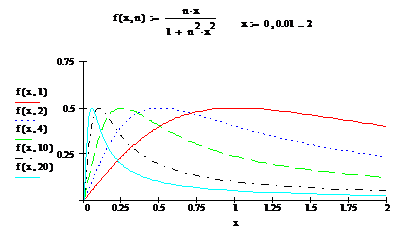
Exemplul
(3). Fie ![]() si sirul de
functii
si sirul de
functii ![]() ,
, ![]() , definit prin relatiile
, definit prin relatiile
![]() .
.
(i).
Calculati ![]() .
.
(ii).
Aratati ca sirul converge uniform catre functia ![]() , oricare ar fi
, oricare ar fi ![]() .
.
Indicatie. (i).
Observam ca ![]() ,
, ![]() . Deoarece functiile
. Deoarece functiile ![]() sunt functii
impare, este suficient sa se studieze convergenta pe intervalul
sunt functii
impare, este suficient sa se studieze convergenta pe intervalul ![]() . Fie
. Fie ![]() , atunci
, atunci ![]() . Pentru
. Pentru ![]() , oarecare, dar fixat, sirul numeric
, oarecare, dar fixat, sirul numeric ![]() are limita
are limita
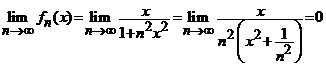 .
.
Asadar, punctele de convergenta ale sirului ![]() apartin
multimii
apartin
multimii![]() . Functia
limita este definita de
. Functia
limita este definita de ![]() ,
, ![]() .
.
(ii).
Din inegalitatea ![]() si
si ![]() rezulta
rezulta ![]() . Asadar, fie
. Asadar, fie ![]() , fixat. Atunci, pentru
, fixat. Atunci, pentru ![]() suficient de mare
putem scrie inegalitatile
suficient de mare
putem scrie inegalitatile
![]() .
.
Este usor de inteles ca
daca alegem ![]() si
si ![]() , atunci
, atunci ![]() , oricare ar fi
, oricare ar fi ![]() .
.
Asadar, putem alege numarul ![]() (aici,
(aici, ![]() reprezinta
functia parte intreaga), care este convenabil pentru orice sir
numeric
reprezinta
functia parte intreaga), care este convenabil pentru orice sir
numeric ![]() ,
, ![]() astfel incat acesta sa
convearga catre functia limita
astfel incat acesta sa
convearga catre functia limita ![]() ,
, ![]() . Deci, sirul de functii
. Deci, sirul de functii ![]() converge uniform pe
converge uniform pe ![]() catre
functia continua
catre
functia continua ![]() . Observam ca
. Observam ca ![]() . Asadar, proprietatea de continuitate a sirului de functii, prin trecere la
limita, cand
. Asadar, proprietatea de continuitate a sirului de functii, prin trecere la
limita, cand ![]() , se transmite functiei limita
, se transmite functiei limita ![]() .
.
Fiecare din functiile ![]() ,
, ![]() au un maxim egal cu
au un maxim egal cu ![]() , care este atins in punctul
, care este atins in punctul ![]() si un minim egal
cu
si un minim egal
cu ![]() , care este atins in punctul
, care este atins in punctul ![]() . Pentru
. Pentru ![]() , valorile extreme tind la zero odata cu punctele
, valorile extreme tind la zero odata cu punctele ![]() care se
deplaseaza, pe axa
care se
deplaseaza, pe axa ![]() catre origine. Convergenta
uniforma a sirului
catre origine. Convergenta
uniforma a sirului ![]() rezulta imediat
din afirmatia
rezulta imediat
din afirmatia ![]() cand
cand ![]() . Intr-adevar, avem
. Intr-adevar, avem
![]() , pentru
, pentru ![]() .
.
Deoarece sirul ![]() converge uniform
catre functia
converge uniform
catre functia ![]() , asa cum observam din fig. 3, daca alegem
, asa cum observam din fig. 3, daca alegem ![]() , atunci
, atunci ![]() si graficele
functiilor
si graficele
functiilor ![]() se afla situate
in banda
se afla situate
in banda ![]() pentru orice
pentru orice ![]() .
.
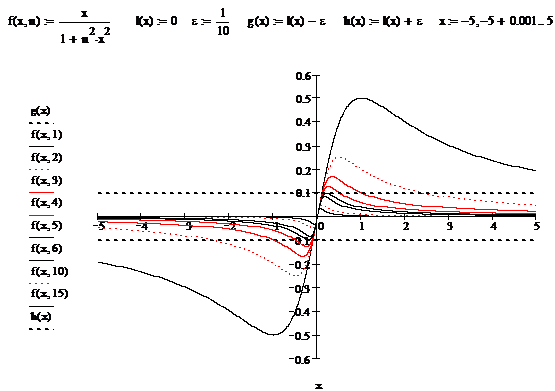
Figura
3. Graficele functiilor ![]() , pentru
, pentru ![]() .
.
Fie ![]() . Atunci
. Atunci
![]() , pentru
, pentru ![]() .
.
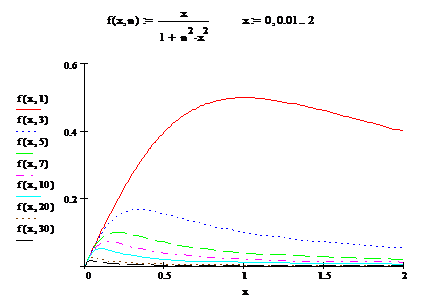
Figura
4. Graficele termenilor sirului din exemplul (3), pentru ![]() .
.
Exemplul (4). Consideram sirul de functii din exemplul (2),
![]() ,
, ![]() .
.
Observam ca ![]() ,
, ![]() . Multimea punctelor
de convergenta a sirului
. Multimea punctelor
de convergenta a sirului ![]() este
este ![]() si functia limita
si functia limita ![]() ,
, ![]() este definita
prin
este definita
prin
![]() .
.
Fie ![]() , oarecare, fixat. Din inegalitatile
, oarecare, fixat. Din inegalitatile ![]() , rezulta ca este suficient sa alegem
, rezulta ca este suficient sa alegem ![]() pentru a avea
pentru a avea ![]() .
.
Se poate verifica, relativ
usor, ca pentru fiecare ![]() , functiile
, functiile ![]() au un maxim egal cu
au un maxim egal cu ![]() care este atins
respectiv, in punctele
care este atins
respectiv, in punctele ![]() (deci
(deci ![]() ). Maximul egal cu
). Maximul egal cu ![]() se deplaseaza
spre stanga cand
se deplaseaza
spre stanga cand ![]() creste, desi pe fiecare verticala fixata
dusa la axa
creste, desi pe fiecare verticala fixata
dusa la axa ![]() punctele graficelor se apropie de axa
punctele graficelor se apropie de axa ![]() , cand
, cand ![]() creste (vezi fig.
4). Daca alegem, de exemplu,
creste (vezi fig.
4). Daca alegem, de exemplu, ![]() oricat am mari pe
oricat am mari pe
![]() este imposibil ca
este imposibil ca ![]() pentru toate valorile
lui
pentru toate valorile
lui ![]() . Asadar, sirul
. Asadar, sirul ![]() .
.
9. Observatie.
In exemplul (4), se prezinta un caz interesant care arata ca
desi sirul de functii nu
converge uniform pe ![]() totusi,
functia limita este continua
pe
totusi,
functia limita este continua
pe ![]() . Intr-adevar, se constata ca functia
limita
. Intr-adevar, se constata ca functia
limita ![]() , este continua pe
, este continua pe ![]() (deci,
(deci, ![]() ).
).
Asadar, proprietatea de continuitate a sirului de
functii, prin trecere la limita, cand ![]() , uneori se poate transmite functiei
limita si in cazul convergentei punctuale.
, uneori se poate transmite functiei
limita si in cazul convergentei punctuale.
Exemplul
(5). Fie ![]() si sirul de
functii
si sirul de
functii ![]() , definit prin
, definit prin ![]() .
.
(i). Determinati multimea punctelor de
convergenta ![]() ale sirului.
ale sirului.
(ii). Fie numarul real ![]() , cu
, cu ![]() . Aratati ca sirul dat converge uniform
pe intervalul
. Aratati ca sirul dat converge uniform
pe intervalul ![]() .
.
(iii).
Sirul converge uniform pe ![]() ?
?
In figurile (5)-(7) sunt reprezentate
graficele functiilor ![]() , pentru
, pentru ![]()
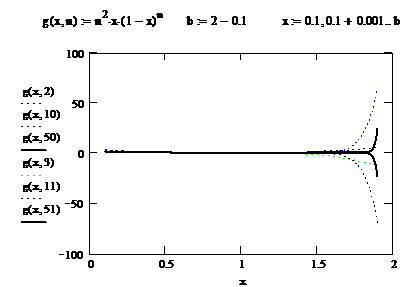
Figura 5. Reprezentarea grafica
a unor functii, din exemplul (5), pe intervalul ![]() .
.
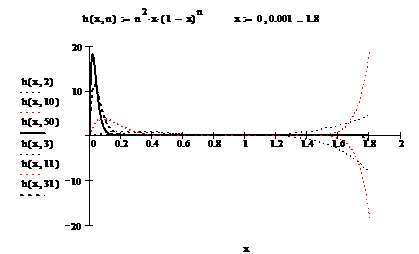
Figura Reprezentarea grafica a unor functii,
din exemplul (5), pe intervalul ![]() .
.
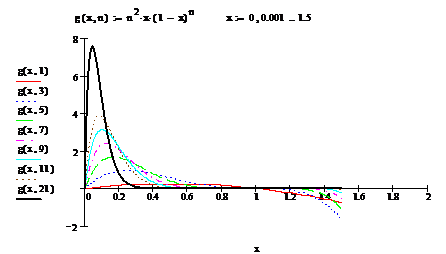
Figura
7. Reprezentarea grafica a unor functii, din exemplul (5), pe
intervalul ![]() .
.
Exercitiul
1. Daca ![]() atunci
atunci ![]() pentru orice
pentru orice ![]() . Reciproc nu este adevarat.
. Reciproc nu este adevarat.
De exemplu sirul ![]() , studiat in exemplul (1), este punctual convergent la functia
, studiat in exemplul (1), este punctual convergent la functia ![]() Deoarece
Deoarece ![]() , atunci
, atunci ![]() cand
cand ![]() si deci, acest
sir nu converge uniform pe
si deci, acest
sir nu converge uniform pe ![]() .
.
10.
Definitie. Sirul
de functii ![]() din
din ![]() se numeste uniform Cauchy daca si numai
daca
se numeste uniform Cauchy daca si numai
daca
![]() astfel incat
astfel incat ![]() oricare ar fi
oricare ar fi ![]() si
si ![]() ,
,
sau echivalent
![]() a.i.
a.i. ![]() ,
, ![]() si
si ![]()
![]()
![]() .
.
Criteriu de convergenta uniforma. Criteriul general al lui Cauchy de la siruri, care stabileste conditia de existenta a limitei finite a sirurilor numerice, conduce la urmatorul criteriu de convergenta uniforma pentru siruri de functii:
11.
Teorema. (Criteriul lui Cauchy) Fie ![]() un sir de
functii din
un sir de
functii din ![]() . Urmatoarele conditii sunt echivalente:
. Urmatoarele conditii sunt echivalente:
(i).
Sirul ![]() admite o functie
limita
admite o functie
limita ![]() si converge uniform catre aceasta in
si converge uniform catre aceasta in ![]() .
.
(ii). Sirul ![]() este uniform Cauchy in
este uniform Cauchy in ![]() .
.
Demonstratie. Implicatia "![]() ", rezulta imediat din definitia uniform
convergentei. Intr-adevar, daca sirul are o functie
limita si converge uniform catre aceasta functie in
multimea
", rezulta imediat din definitia uniform
convergentei. Intr-adevar, daca sirul are o functie
limita si converge uniform catre aceasta functie in
multimea ![]() , atunci pentru orice
, atunci pentru orice ![]() exista
exista ![]() , independent de
, independent de ![]() , a.i.
, a.i. ![]() , sa avem
, sa avem ![]() , pentru orice
, pentru orice ![]() . Analog, avem
. Analog, avem ![]() , oricare ar fi
, oricare ar fi ![]() Din aceste inegalitati rezulta
Din aceste inegalitati rezulta
![]() .
.
"![]() ". Pentru a demonstra aceasta implicatie
(adica, conditia suficienta) vom presupune ca sirul
este uniform Cauchy. Atunci oricare ar fi
". Pentru a demonstra aceasta implicatie
(adica, conditia suficienta) vom presupune ca sirul
este uniform Cauchy. Atunci oricare ar fi ![]() , fixat, sirul
, fixat, sirul ![]() este un sir
numeric care este sir Cauchy de numere reale si, potrivit criteriului
general al lui Cauchy este convergent. Prin urmare, pentru acest sir
exista o limita finita
este un sir
numeric care este sir Cauchy de numere reale si, potrivit criteriului
general al lui Cauchy este convergent. Prin urmare, pentru acest sir
exista o limita finita ![]() . Cum
. Cum ![]() este ales oarecare, atunci se pune in evidenta
functia
este ales oarecare, atunci se pune in evidenta
functia ![]() , ceea ce arata existenta functiei limita
, ceea ce arata existenta functiei limita
![]() pentru sirul
considerat. Scriind ca sirul este uniform Cauchy si luand
pentru sirul
considerat. Scriind ca sirul este uniform Cauchy si luand ![]() (
(![]() si
si ![]() fixati)
rezulta (i).
fixati)
rezulta (i).
12. Teorema. (Criteriul de convergenta
uniforma). Fie ![]() un sir de
functii din
un sir de
functii din ![]() ,
, ![]() si
si ![]() un sir de numere
reale pozitive, convergent la zero. Daca exista
un sir de numere
reale pozitive, convergent la zero. Daca exista ![]() a.i.
a.i. ![]() si oricare ar fi
si oricare ar fi ![]() sa avem
sa avem ![]() , atunci
, atunci ![]() .
.
Un criteriu
de convergenta uniforma in algebra Banach ![]() este dat de
urmatoarea
este dat de
urmatoarea
13.
Teorema. (Teorema lui Dini). Fie ![]() un spatiu metric compact si
un spatiu metric compact si ![]() . Presupunem indeplinite conditiile:
. Presupunem indeplinite conditiile:
(i).
Sirul ![]() este punctual convergent la o functie
este punctual convergent la o functie ![]() ,
,
(ii).
Sirul ![]() este monoton (crescator sau
descrescator),
este monoton (crescator sau
descrescator),
atunci sirul ![]() converge uniform la functia
converge uniform la functia ![]() (adica converge
catre
(adica converge
catre ![]() in spatiul Banach
in spatiul Banach
![]() ).
).
Demonstratie. Presupunem ca sirul ![]() este crescator
si cum
este crescator
si cum ![]() este spatiu
metric compact
este spatiu
metric compact ![]()
![]() ,
, ![]() si oricare ar fi
si oricare ar fi ![]() . Deci,
. Deci, ![]() este marginita
superior.
este marginita
superior.
Convergenta uniforma a sirului
![]() la functia
continua
la functia
continua ![]() revine la verificarea
conditiei:
revine la verificarea
conditiei:
![]() astfel incat
astfel incat ![]() oricare ar fi
oricare ar fi ![]() ,
,
echivalenta cu ![]() a.i. pentru
a.i. pentru ![]() sa avem
sa avem ![]() . Din faptul ca sirul a fost presupus
crescator ultima inegalitate se scrie
. Din faptul ca sirul a fost presupus
crescator ultima inegalitate se scrie![]() ,
, ![]() . Deoarece
. Deoarece ![]() atunci functiile
"
atunci functiile
"![]() " sunt continue pe
" sunt continue pe ![]() , spatiu metric compact, si potrivit teoremei lui
Weierstrwss, acestea sunt marginite si isi ating marginile. In consecinta, este suficient sa
demonstram ca are loc inegalitatea
, spatiu metric compact, si potrivit teoremei lui
Weierstrwss, acestea sunt marginite si isi ating marginile. In consecinta, este suficient sa
demonstram ca are loc inegalitatea ![]() ,
, ![]() si
si ![]() .
.
In acest scop, notam cu
![]() ,
, ![]() .
.
Atunci
(1). ![]() sunt multimi
deschise (pentru ca
sunt multimi
deschise (pentru ca ![]() sunt functii
continue);
sunt functii
continue);
(2). Au loc incluziunile ![]() ,
, ![]() ;
;
(3). ![]() .
.
Conditia (i) se scrie: oricare ar fi ![]() , dar fixat, sirul numeric
, dar fixat, sirul numeric ![]() converge catre
numarul
converge catre
numarul ![]() . Deci, pentru
. Deci, pentru ![]() suficient de mare
rezulta ca
suficient de mare
rezulta ca ![]() . Deoarece,
. Deoarece, ![]() este spatiu
metric compact si
este spatiu
metric compact si ![]() este o acoperire a lui
este o acoperire a lui
![]() cu multimi
deschise ascendente (proprietatea (2)), rezulta ca putem extrage o
subacoperire finita a lui
cu multimi
deschise ascendente (proprietatea (2)), rezulta ca putem extrage o
subacoperire finita a lui ![]() . Asadar, exista
. Asadar, exista ![]() a.i.
a.i. ![]() si deci
si deci ![]() , pentru
, pentru ![]() si, potrivit
definitiei lui
si, potrivit
definitiei lui ![]() , avem
, avem ![]() oricare ar fi
oricare ar fi ![]() si
si ![]() .
.
14. Aplicatie.
Fie ![]() si
si ![]() , definita prin
, definita prin ![]() . Atunci exista un sir de polinoame (functii
de o variabila reala)
. Atunci exista un sir de polinoame (functii
de o variabila reala) ![]() care converg uniform
la functia
care converg uniform
la functia ![]() in
in ![]() . Altfel spus, convergenta sirului de polinoame
. Altfel spus, convergenta sirului de polinoame ![]() catre
catre ![]() are loc in norma
convergentei uniforme, in spatiul Banach
are loc in norma
convergentei uniforme, in spatiul Banach ![]() .
.
Construim, prin inductie dupa ![]() , sirul de polinoame definit astfel:
, sirul de polinoame definit astfel:
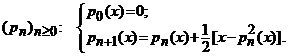
Acest sir are proprietatile:
(1).
Este un sir crescator, ![]() ;
;
(2).
![]() , pentru orice
, pentru orice ![]() si orice
si orice ![]() .
.
Intr-adevar, pentru ![]()
![]()
![]() . Fie
. Fie ![]() , atunci
, atunci ![]() ,
, ![]() . Aceasta inegalitate, impreuna cu
. Aceasta inegalitate, impreuna cu
![]() ,
, ![]() ,
,
arata ca ![]() pentru orice
pentru orice ![]() .
.
Presupunand proprietatea adevarata
pentru ![]() adica,
adica, ![]() , pentru orice
, pentru orice ![]() , aratam ca inegalitatile (2) au loc
si pentru
, aratam ca inegalitatile (2) au loc
si pentru ![]() .
.
Avem
![]() ,
,
deci, ![]() (am folosit
(am folosit ![]() ).
).
Pe de alta parte, pentru orice ![]() deducem ca
deducem ca ![]() .
.
Asadar, pentru orice ![]() , sirul de polinoame
, sirul de polinoame ![]() este crescator
si marginit superior, pe acest interval, de functia
este crescator
si marginit superior, pe acest interval, de functia ![]() . Atunci, potrivit teoremei lui Dini, el este convergent
catre o functie, notata cu
. Atunci, potrivit teoremei lui Dini, el este convergent
catre o functie, notata cu ![]() .
.
Prin trecerea la limita in
relatia de recurenta, obtinem, cand ![]() ,
, ![]() , de unde rezulta
, de unde rezulta ![]() si, in
consecinta,
si, in
consecinta, ![]() . Mai mult, datorita teoremei lui Dini, sirul de
polinoame converge uniform catre functia
. Mai mult, datorita teoremei lui Dini, sirul de
polinoame converge uniform catre functia ![]() .
.
15.
Lema. Fie ![]() un spatiu metric,
un spatiu metric,
![]() si
si ![]() . Proprietatile urmatoare sunt echivalente:
. Proprietatile urmatoare sunt echivalente:
i). ![]() (s-a notat cu
(s-a notat cu ![]() multimea
punctelor aderente multimii
multimea
punctelor aderente multimii ![]() ).
).
ii). Exista un sir ![]() astfel incat
astfel incat ![]() , cand
, cand ![]() .
.
Demonstratie. Aratam implicatia ![]() . Fie
. Fie ![]() . Cum
. Cum ![]() rezulta ca
punctul
rezulta ca
punctul ![]() este punct aderent
multimii
este punct aderent
multimii ![]() si deci orice
vecinatate a lui
si deci orice
vecinatate a lui ![]() contine un punct
din
contine un punct
din ![]() . Asadar,
. Asadar, ![]() ,
, ![]() . Daca punem
. Daca punem ![]() , atunci avem
, atunci avem ![]() .
.
Implicatia ![]() este evidenta.
este evidenta.
1 Definitie. Fie
![]() un spatiu metric,
un spatiu metric,
![]() . Daca
. Daca ![]() se spune ca
elementul
se spune ca
elementul ![]() este aproximabil prin elemente din
este aproximabil prin elemente din ![]() . In cazul spatiului
. In cazul spatiului ![]() inzestrat cu metrica
lui Cebasev si
inzestrat cu metrica
lui Cebasev si ![]() atunci elementul
atunci elementul ![]() se numeste uniform aproximabil prin elemente din
se numeste uniform aproximabil prin elemente din ![]() .
.
17.
Teorema. Fie ![]() un spatiu metric
si sirul de functii
un spatiu metric
si sirul de functii ![]() . Daca sirul
. Daca sirul ![]() converge uniform pe
converge uniform pe ![]() la functia
la functia ![]() , atunci
, atunci ![]() .
.
Demonstratie. Fie ![]() , deoarece sirul
, deoarece sirul ![]() converge uniform pe
converge uniform pe ![]() la functia
la functia ![]() , atunci exista
, atunci exista ![]() a.i. pentru orice
a.i. pentru orice ![]() si
si ![]() sa avem
sa avem ![]() .
.
Fie ![]() un punct de
continuitate al functiilor
un punct de
continuitate al functiilor ![]() . Pentru orice
. Pentru orice ![]() ,
, ![]() fixat, avem in
particular,
fixat, avem in
particular, ![]() . Intrucat functia
. Intrucat functia ![]() (cu
(cu ![]() fixat) este
continua in
fixat) este
continua in ![]() rezulta ca
exista o vecinatate
rezulta ca
exista o vecinatate ![]() a.i. sa avem
a.i. sa avem ![]() , pentru orice
, pentru orice ![]() . Din aceste relatii, pentru orice
. Din aceste relatii, pentru orice ![]() , deducem
, deducem
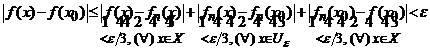 ,
,
ceea ce arata ca functia limita ![]() este continua in
este continua in ![]() . Cum
. Cum ![]() a fost ales arbitrar
in
a fost ales arbitrar
in ![]() , rezulta ca
, rezulta ca ![]() este continua pe
este continua pe ![]() .
.
18. Observatie.
Conditia din teorema 17 este numai o conditie
suficienta pentru ca functia limita sa fie
continua: continuitatea sirului de functii uniform convergent ![]() in orice punct
in orice punct ![]() atrage continuitatea
functiei limita
atrage continuitatea
functiei limita ![]() in orice punct
in orice punct ![]() . Daca
. Daca ![]() este un sir de
functii continue si functia limita
este un sir de
functii continue si functia limita ![]() nu este continua
in orice punct din
nu este continua
in orice punct din ![]() , atunci sirul
, atunci sirul ![]() nu converge uniform pe
nu converge uniform pe ![]() .
.
Daca sirul de functii
continue ![]() este punctual
convergent (deci converge in toate punctele din
este punctual
convergent (deci converge in toate punctele din ![]() ), atunci este posibil ca functia limita sa nu
fie continua in orice punct
), atunci este posibil ca functia limita sa nu
fie continua in orice punct ![]() (vezi exemplul 1). In exemplul 4, desi sirul
converge punctual totusi functia limita este continua.
(vezi exemplul 1). In exemplul 4, desi sirul
converge punctual totusi functia limita este continua.
Exista siruri de functii continue pe portiuni pe ![]() care converg uniform
pe acest interval catre o functie continua pe
care converg uniform
pe acest interval catre o functie continua pe ![]() . De exemplu sirul de functii
. De exemplu sirul de functii ![]() discontinue in punctul
discontinue in punctul
![]() , converge uniform pe
, converge uniform pe ![]() catre
functia continua
catre
functia continua ![]() . Intr-adevar, convergenta uniforma
rezulta din
. Intr-adevar, convergenta uniforma
rezulta din
![]() cand
cand ![]() .
.
19.
Teorema. Fie ![]() o multime si
o multime si
![]() multimea
functiilor reale marginite pe
multimea
functiilor reale marginite pe ![]() . Daca
. Daca ![]() este un sir de
functii din
este un sir de
functii din ![]() care converge uniform
pe
care converge uniform
pe ![]() la functia
la functia ![]() , atunci
, atunci ![]() .
.
Demonstratie. Norma unui element ![]() se defineste prin
se defineste prin
![]() . In spatiul
. In spatiul ![]() , convergenta fata de aceasta norma
este cea uniforma.
, convergenta fata de aceasta norma
este cea uniforma.
Fie ![]() , deoarece sirul
, deoarece sirul ![]() converge uniform pe
converge uniform pe ![]() la functia
la functia ![]() , atunci exista
, atunci exista ![]() a.i. pentru orice
a.i. pentru orice ![]() sa avem
sa avem ![]() .
.
Din aceasta inegalitate, prin trecere la
limita cand ![]() , obtinem.
, obtinem. ![]() , pentru orice
, pentru orice ![]() . Atunci, pentru orice
. Atunci, pentru orice ![]() avem
avem
![]() .
.
Cum ![]() rezulta ca
rezulta ca ![]() si, in
consecinta, avem
si, in
consecinta, avem ![]() ceea ce arata ca
ceea ce arata ca ![]() .
.
20.
Teorema. Fie ![]() si
si ![]() un sir de
functii din
un sir de
functii din ![]() cu
proprietatile:
cu
proprietatile:
(1). Functiile ![]() sunt continue pe portiuni;
sunt continue pe portiuni;
(2). Sirul ![]() converge uniform in
toate punctele de continuitate
converge uniform in
toate punctele de continuitate ![]() la functia
la functia ![]() ,
,
atunci ![]() este continua pe
portiuni si in plus, avem
este continua pe
portiuni si in plus, avem
![]() .
.
Demonstratie. Continuitatea pe portiuni a
functiei limita ![]() rezulta din
teorema 17. Deoarece functiile
rezulta din
teorema 17. Deoarece functiile ![]() si
si ![]() sunt continue pe
portiuni atunci, tinand seama de proprietatea de aditivitate a
integralei de interval, aceste
functii sunt integrabile pe
sunt continue pe
portiuni atunci, tinand seama de proprietatea de aditivitate a
integralei de interval, aceste
functii sunt integrabile pe ![]() . Folosind uniform convergenta sirului de
functii catre functia limita atunci cand
. Folosind uniform convergenta sirului de
functii catre functia limita atunci cand ![]() , avem
, avem
![]()
Exercitiul
2. Fie sirul de
functii continue ![]() , definit prin
, definit prin ![]() ,
, ![]() . Atunci
. Atunci
(a). Sirul ![]() converge (punctual) in
toate punctele intervalului
converge (punctual) in
toate punctele intervalului ![]() catre
functia
catre
functia ![]() , data de
, data de
![]() . (
. (![]() discontinua in punctul
discontinua in punctul ![]() )
)
(b). Deoarece ![]() daca
daca ![]() si
si ![]() daca
daca ![]() , atunci
, atunci ![]() , ceea ce arata ca sirul
, ceea ce arata ca sirul ![]() nu converge uniform pe
nu converge uniform pe
![]() (vezi si
observatia 18).
(vezi si
observatia 18).
(c). Functiile ![]() si
si ![]() sunt integrabile pe
sunt integrabile pe ![]() si avem
si avem
![]()
![]() ;
;
Pentru ![]() , constatam ca desi sirul nu converge
uniform pe
, constatam ca desi sirul nu converge
uniform pe ![]() totusi, limita
integralei este egala cu integrala limitei:
totusi, limita
integralei este egala cu integrala limitei:
![]() .
.
Aceasta se explica prin faptul ca
sirul ![]() este uniform
convergent pe orice interval inchis
este uniform
convergent pe orice interval inchis ![]() fixat si atunci
putem scrie
fixat si atunci
putem scrie
![]() .
.
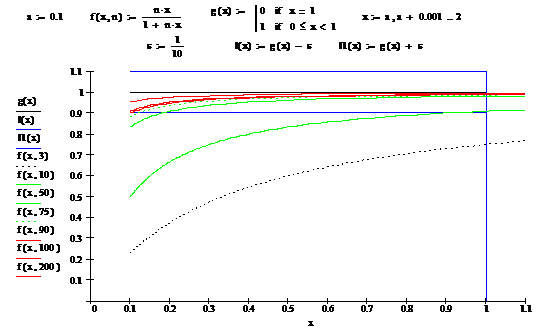
Figura 8. Uniform convergenta
sirului ![]() , pe intervalul
, pe intervalul ![]()
Aratam ca prin trecere la
limita cand ![]() egalitatea inca
se pastreaza. In acest scop vom scrie integrala de la
egalitatea inca
se pastreaza. In acest scop vom scrie integrala de la ![]() la
la ![]() sub forma
sub forma
![]() . (*)
. (*)
Din inegalitatile
![]() ,
,
deducem ca sirul ![]() este subunitar oricare
ar fi
este subunitar oricare
ar fi ![]() si atunci, este
de asteptat ca pentru
si atunci, este
de asteptat ca pentru ![]() suficient de mic
si orice
suficient de mic
si orice ![]() , prima integrala din membrul drept al relatiei (*)
poate fi facuta oricat de mica dorim. Intr-adevar, este
suficient sa alegem de exemplu,
, prima integrala din membrul drept al relatiei (*)
poate fi facuta oricat de mica dorim. Intr-adevar, este
suficient sa alegem de exemplu, ![]() si atunci
si atunci
![]() .
.
Asadar, integrala ![]() poate fi
facuta oricat de mica dorim si valoarea sa, prin trecere la
limita cand
poate fi
facuta oricat de mica dorim si valoarea sa, prin trecere la
limita cand ![]() nu modifica limita
nu modifica limita ![]() .
.
In concluzie, desi convergenta
sirului ![]() nu este uniforma
pe
nu este uniforma
pe ![]() , totusi avem egalitatea
, totusi avem egalitatea
![]() .
.
21.
Teorema. Fie ![]() un interval deschis si
un interval deschis si
![]() un sir de
functii din
un sir de
functii din ![]() care verifica proprietatile:
care verifica proprietatile:
(1). Functiile ![]() sunt diferentiabile pe
sunt diferentiabile pe ![]() (deci, derivabile pe
(deci, derivabile pe ![]() );
);
(2). Sirul derivatelor, ![]() converge uniform pe
converge uniform pe ![]() la functia
la functia ![]() ;
;
(3). Exista ![]() a.i. sirul
numeric
a.i. sirul
numeric ![]() este convergent;
este convergent;
atunci
(i). sirul ![]() este uniform
convergent pe
este uniform
convergent pe ![]() la functia
la functia ![]() ;
;
(ii). ![]() este
diferentiabila pe
este
diferentiabila pe ![]() si
si ![]() .
.
Demonstratie. Deoarece functiile ![]() sunt diferentiabile pe
sunt diferentiabile pe ![]() , atunci aceste functii sunt diferentiabile in
punctul
, atunci aceste functii sunt diferentiabile in
punctul ![]() .
.
Din conditia de diferentiabilitate
in punctul ![]() rezulta ca
exista functiile
rezulta ca
exista functiile ![]() continue in
continue in ![]() si
si ![]() , a.i.
, a.i.
![]() , (*)
, (*)
Pasul 1. Aratam ca sirul de
functii ![]() converge uniform pe
converge uniform pe ![]() la functia
la functia ![]() ,
, ![]() este continua in
este continua in ![]() si
si ![]() .
.
Datorita relatiilor (*), sirul
de functii ![]() , definit prin
, definit prin
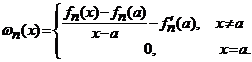
este un sir de functii continue. Aratam ca
sirul ![]() , astfel definit, este uniform Cauchy pe
, astfel definit, este uniform Cauchy pe ![]() si deci, este uniform
convergent pe intervalul
si deci, este uniform
convergent pe intervalul ![]() . Intr-adevar, putem scrie
. Intr-adevar, putem scrie
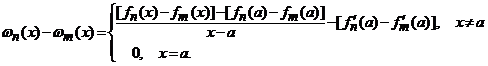
Introducem notatia ![]() . Atunci
. Atunci ![]() ,
, ![]() si din ipotez (1)
rezulta ca
si din ipotez (1)
rezulta ca ![]() este derivabila
pe
este derivabila
pe ![]() . Asadar, putem aplica teorema lui Lagrange pe
intervalul
. Asadar, putem aplica teorema lui Lagrange pe
intervalul ![]() ,
, ![]() . Deci exista
. Deci exista ![]() a.i. sa avem
a.i. sa avem
![]() .
.
Asadar, putem scrie
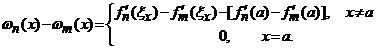
Potrivit conditiei (2) din teorema,
fiind dat ![]() , exista
, exista ![]() a.i. sa avem
a.i. sa avem
![]() .
.
Deci, rezulta
![]() ,
,
ceea ce arata ca sirul ![]() este uniform Cauchy pe
este uniform Cauchy pe
![]() deci, este uniform
convergent pe
deci, este uniform
convergent pe ![]() . Asadar, exista functia
. Asadar, exista functia ![]() ,
, ![]() este continua in
este continua in ![]() (teorema 17) si evident
(teorema 17) si evident ![]() .
.
Pasul 2. Aratam ca sirul ![]() converge uniform la
functia
converge uniform la
functia ![]() , care satisface egalitatea
, care satisface egalitatea
![]() . (**)
. (**)
Aceasta relatie arata ca functia ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() si
si ![]() .
.
Intr-adevar, din teorema lui Lagrange
si din conditiile (2) si (3) deducem ca sirul ![]() este uniform Cauchy pe
este uniform Cauchy pe
![]() si deci, converge
uniform la functia
si deci, converge
uniform la functia ![]() . Daca trecem la limita in relatia (*),
folosind convergenta uniforma a sirului
. Daca trecem la limita in relatia (*),
folosind convergenta uniforma a sirului ![]() , deducem relatia (**).
, deducem relatia (**).
Pasul 3. Fie ![]() , din pasul 2 rezulta ca sirul numeric
, din pasul 2 rezulta ca sirul numeric ![]() converge catre
converge catre ![]() . Asadar, conditiile (1) si (3) din
teorema sunt verificate pentru
. Asadar, conditiile (1) si (3) din
teorema sunt verificate pentru ![]() si, datorita
pasului 2, cu
si, datorita
pasului 2, cu ![]() , avem
, avem ![]() . Cum
. Cum ![]() a fost ales arbitrar,
rezulta ca
a fost ales arbitrar,
rezulta ca ![]() este derivabila
in orice punct din
este derivabila
in orice punct din ![]() .
.
22. Teorema. Fie
![]() un interval inchis.
Atunci orice functie
un interval inchis.
Atunci orice functie ![]() admite o
primitiva.
admite o
primitiva.
Demonstratie. Intervalul ![]() fiind compact si
fiind compact si ![]() continua pe
continua pe ![]() atunci
atunci ![]() este uniform
aproximabila pe
este uniform
aproximabila pe ![]() prin polinoame.
Adica exista un sir
prin polinoame.
Adica exista un sir ![]() de functii
polinomiale de o variabila care converg uniform pe
de functii
polinomiale de o variabila care converg uniform pe ![]() la functia
la functia ![]() . Pentru orice polinom
. Pentru orice polinom ![]() exista
exista ![]() ,
, ![]() primitiva a lui
primitiva a lui ![]() , cu
, cu ![]() , care verifica conditiile:
, care verifica conditiile:
(1). Functiile ![]() sunt
diferentiabile pe
sunt
diferentiabile pe ![]() oricare ar fi
oricare ar fi ![]() si
si ![]() pe
pe ![]() ;
;
(2). Sirul derivatelor, ![]() (care coincide cu
sirul polinoamelor) converge uniform pe
(care coincide cu
sirul polinoamelor) converge uniform pe ![]() la
la ![]() ;
;
(3). Sirul numeric ![]() este convergent.
este convergent.
Atunci, ![]() verifica
conditiile teoremei 21 si deci, sirul
verifica
conditiile teoremei 21 si deci, sirul ![]() este uniform
convergent la functia
este uniform
convergent la functia ![]() ,
, ![]() este
diferentiabila pe
este
diferentiabila pe ![]() si
si ![]() .
.
Serii de functii
Fie![]() un spatiu metric si
un spatiu metric si ![]() spatiul vectorial
al functiilor definite pe
spatiul vectorial
al functiilor definite pe ![]() cu valori reale.
cu valori reale.
23.
Definitie. Fie 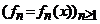 un sir de
functii din
un sir de
functii din ![]() si sirul sumelor partiale
si sirul sumelor partiale ![]() , definit prin
, definit prin ![]() .
.
Perechea ![]() se numeste serie de functii din
se numeste serie de functii din ![]() si se noteaza prin
si se noteaza prin
![]() sau
sau 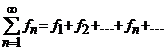 (1)
(1)
Termenul general ![]() al seriei este o
functie de
al seriei este o
functie de ![]() , astfel ca
, astfel ca
![]() ,
,
este o functie bine definita (suma unui numar finit de functii este o functie bine definita) si restul seriei de functii este definit prin
![]() ,
,
unde am notat suma
seriei cu ![]() .
.
24. Observatie.
Pentru fiecare punct ![]() fixat, consideram
seria numerica
fixat, consideram
seria numerica
![]()
formata cu valorile functiilor din
sirul ![]() , calculate in punctul
, calculate in punctul ![]() . Deoarece suma seriei numerice convergente este
determinata de valoarea lui
. Deoarece suma seriei numerice convergente este
determinata de valoarea lui ![]() , atunci este natural ca ea sa reprezinte o functie
de
, atunci este natural ca ea sa reprezinte o functie
de ![]() .
.
Putem aplica seriilor de
functii atat considerentele facute la seriile numerice cat si
cele facute la siruri de functii. Pentru aceasta este suficient
sa remarcam ca daca ![]() sunt functii
continue respectiv derivabile pe
sunt functii
continue respectiv derivabile pe ![]() , atunci
, atunci ![]() , ca suma finita de termeni, este o functie
continua, respectiv derivabila.
, ca suma finita de termeni, este o functie
continua, respectiv derivabila.
25.
Definitie. Seria de
functii ![]() se numeste punctual (simplu) convergenta
pe
se numeste punctual (simplu) convergenta
pe ![]() daca si
numai daca sirul sumelor
partiale
daca si
numai daca sirul sumelor
partiale ![]() din
din ![]() asociat seriei, este punctual convergent
pe
asociat seriei, este punctual convergent
pe ![]() .
.
Daca pentru orice ![]() fixat,
fixat, ![]() (sirul de numere
(sirul de numere ![]() converge catre limita
converge catre limita
![]() ), atunci functia
), atunci functia ![]() se numeste suma punctuala a seriei de
functii considerata si notam
se numeste suma punctuala a seriei de
functii considerata si notam
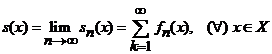 (2)
(2)
Altfel spus, seria de functii ![]() este punctual
convergenta pe
este punctual
convergenta pe ![]() catre
functia
catre
functia ![]() , daca si numai daca seria numerica
, daca si numai daca seria numerica ![]() converge in fiecare
punct
converge in fiecare
punct ![]() (
(![]() fixat) si vom scrie:
fixat) si vom scrie:
![]() si
si ![]() , exista un numar natural
, exista un numar natural ![]() a.i.
a.i. ![]() sa avem
sa avem ![]() .
.
2 Definitie. Seria de functii ![]() se zice uniform convergenta pe
se zice uniform convergenta pe ![]() catre
functia
catre
functia ![]() daca si
numai daca sirul
daca si
numai daca sirul ![]() din
din ![]() este uniform convergent pe
este uniform convergent pe ![]() si scriem
si scriem ![]() .
.
Daca sirul ![]() converge uniform,
atunci functia limita
converge uniform,
atunci functia limita ![]() se numeste suma uniforma a seriei de
functii date pe
se numeste suma uniforma a seriei de
functii date pe ![]() si notam
si notam
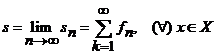 , (3)
, (3)
Altfel spus, seria de functii ![]() este uniform
convergenta pe
este uniform
convergenta pe ![]() catre
functia limita
catre
functia limita ![]() daca si numai
daca
daca si numai
daca
![]() , exista un numar natural
, exista un numar natural ![]() a.i.
a.i. ![]() si
si ![]() sa avem
sa avem ![]() .
.
27.
Definitie. Seria de
functii ![]() se numeste absolut convergenta in punctul
se numeste absolut convergenta in punctul ![]() daca si
numai daca seria numerica
daca si
numai daca seria numerica ![]() este
convergenta.
este
convergenta.
Seria de functii ![]() se numeste absolut convergenta pe
se numeste absolut convergenta pe ![]() daca si
numai daca este absolut convergenta in fiecare punct din
daca si
numai daca este absolut convergenta in fiecare punct din ![]() .
.
Multimea ![]() formata din toate
punctele de convergenta ale
seriei de functii
formata din toate
punctele de convergenta ale
seriei de functii ![]() se numeste multimea de convergenta a
seriei de functii considerate.
se numeste multimea de convergenta a
seriei de functii considerate.
28. Propozitie.
Daca seria de functii ![]() este absolut
convergenta in punctul
este absolut
convergenta in punctul ![]() atunci seria este
convergenta in punctul
atunci seria este
convergenta in punctul ![]() .
.
Criterii de convergenta uniforma a seriilor de functii
29.
Criteriul lui Cauchy. Fie
seria de functii ![]() din
din ![]() . Urmatoarele afirmatii sunt echivalente:
. Urmatoarele afirmatii sunt echivalente:
Seria de functii ![]() este uniform
convergenta pe
este uniform
convergenta pe ![]() ;
;
2). ![]() , exista
, exista ![]() a.i.
a.i. ![]() ,
, ![]() si
si ![]() sa avem
sa avem ![]()
(adica, sirul sumelor partiale asociat seriei de functii este uniform Cauchy);
30. Observatie.
Daca termenii seriei de functii (1), uniform convergenta pe ![]() , se inmultesc cu o functie
, se inmultesc cu o functie ![]() marginita pe
marginita pe![]() ,
, ![]() , atunci obtinem o serie uniform convergenta pe
, atunci obtinem o serie uniform convergenta pe ![]()
31.
Criteriul lui Weierstrass.
Fie seria de functii ![]() din
din ![]() . Presupunem verificate conditiile:
. Presupunem verificate conditiile:
Seria numerica ![]() , avand termenii
pozitivi
, avand termenii
pozitivi ![]() , este
convergenta;
, este
convergenta;
(2). Exista numarul natural ![]() a.i.
a.i. ![]() ,
, ![]() , si
, si ![]() .
.
Atunci seria de functii
este uniform convergenta pe ![]() .
.
De exemplu, seriile de functii ![]() si
si![]() , sunt uniform convergente pe un interval oarecare daca
seria numerica
, sunt uniform convergente pe un interval oarecare daca
seria numerica ![]() este absolut
convergenta.
este absolut
convergenta.
Intr-adevar, deoarece 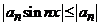 si
si ![]() , atunci seria convergenta
, atunci seria convergenta ![]() este serie
majoranta a seriilor de functii date.
este serie
majoranta a seriilor de functii date.
32. Teorema.
Fie seria de functii ![]() din
din ![]() . Daca aceasta serie este uniform convergenta
pe
. Daca aceasta serie este uniform convergenta
pe ![]() catre
functia
catre
functia ![]() (adica,
(adica, ![]() ) atunci
) atunci ![]() .
.
33.
Teorema. Fie ![]() un interval si
seria de functii
un interval si
seria de functii ![]() din
din ![]() . Daca aceasta serie este uniform convergenta
pe
. Daca aceasta serie este uniform convergenta
pe ![]() si
si ![]() , atunci
, atunci
(1). functia ![]() si deci
integrabila pe
si deci
integrabila pe ![]() ;
;
(2). 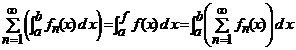 .
.
34.
Teorema. Fie ![]() un interval si
seria de functii
un interval si
seria de functii ![]() . Presupunem verificate conditiile:
. Presupunem verificate conditiile:
(1). functiile ![]() sunt de clasa
sunt de clasa ![]() pe intervalul
pe intervalul ![]() ;
;
(2). seria de functii ![]() este uniform
convergenta pe
este uniform
convergenta pe ![]() avand suma
avand suma ![]() ;
;
(3). seria ![]() este uniform
convergenta pe
este uniform
convergenta pe ![]() avand suma
avand suma ![]() (deci,
(deci, ![]() este functie continua pe
este functie continua pe ![]() ).
).
Atunci functia ![]() este derivabila
pe
este derivabila
pe ![]() si avem
si avem ![]() pentru orice
pentru orice ![]() .
.
35. Observatie. Teorema afirma ca daca sunt verificate conditiile de mai sus, atunci seria de functii poate fi derivata termen cu termen si conditia (3) se poate scrie astfel:
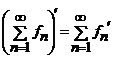 .
.
3 Teorema. Fie ![]() un interval si
seria de functii
un interval si
seria de functii ![]() . Presupunem verificate conditiile:
. Presupunem verificate conditiile:
(1). functiile ![]() sunt de clasa
sunt de clasa ![]() pe intervalul
pe intervalul ![]() ;
;
(2). exista punctul![]() a.i. seria de functii
a.i. seria de functii ![]() este convergenta
avand suma
este convergenta
avand suma ![]() ;
;
(3). seria ![]() este uniform
convergenta pe
este uniform
convergenta pe ![]() avand suma
avand suma ![]() (deci,
(deci, ![]() este functie continua pe
este functie continua pe ![]() ).
).
Atunci seria de functii ![]() converge uniform pe
converge uniform pe ![]() catre
functia
catre
functia ![]() ,
, ![]() este derivabila
pe
este derivabila
pe ![]() si avem
si avem ![]() pentru orice
pentru orice ![]() .
.
Exercitii: (1). Sa se arate ca seria ![]() este uniform
convergenta pe
este uniform
convergenta pe ![]() .
.
Seria de functii ![]() este absolut convergenta
pentru
este absolut convergenta
pentru ![]() si
divergenta pentru
si
divergenta pentru ![]() .
.
Fie 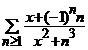 ,
, ![]() . Aratati ca seria converge uniform pe
. Aratati ca seria converge uniform pe![]() catre o functie continua pe
catre o functie continua pe ![]() .
.
Indicatie. Din 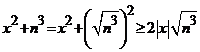 ,
, ![]() , deducem ca termenii
, deducem ca termenii 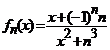 , ai seriei date, admit
majorarea:
, ai seriei date, admit
majorarea: 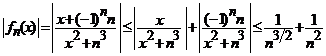 .
.
Deoarece termenii seriei ![]() , sunt functii continue oricare ar fi
, sunt functii continue oricare ar fi ![]() si acestia sunt
majorati de termenii unei serii numerice convergente, atunci seria
data este uniform convergenta pe
si acestia sunt
majorati de termenii unei serii numerice convergente, atunci seria
data este uniform convergenta pe ![]() . Potrivit teoremei 32, suma seriei este functie
continua pe
. Potrivit teoremei 32, suma seriei este functie
continua pe ![]() .
.
Serii de puteri de variabila reala
6,37,
Definitie. Se
numeste serie de puteri ale
variabilei reale ![]() o serie de forma
o serie de forma
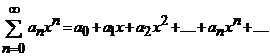 , (4)
, (4)
unde constantele ![]() (sau
(sau ![]() ) se numesc coeficientii
seriei de puteri.
) se numesc coeficientii
seriei de puteri.
38. Observatie. Polinoamele sunt serii de
puteri pentru orice ![]() (numite functii intregi) de un tip particular, unde
(numite functii intregi) de un tip particular, unde ![]() iar k este gradul polinomului respectiv.
iar k este gradul polinomului respectiv.
39.
Teorema. (Abel, 1826).
Pentru orice serie de puteri 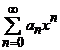 , putem asocia un numar real pozitiv
, putem asocia un numar real pozitiv ![]() (eventual nul sau infinit) astfel incat:
(eventual nul sau infinit) astfel incat:
(i). seria ![]() converge absolut
pentru orice
converge absolut
pentru orice![]() , cu
, cu ![]() ;
;
(ii). seria ![]() este divergenta
pentru orice
este divergenta
pentru orice ![]() cu
cu ![]() .
.
Demonstratie. (i).
Fie ![]() a.i. seria
numerica
a.i. seria
numerica ![]() este convergenta
(exista numarul
este convergenta
(exista numarul ![]() (!), eventual
(!), eventual ![]() ). Atunci
). Atunci ![]() a.i.
a.i. ![]() . Asadar, daca exista
. Asadar, daca exista ![]() , avem
, avem
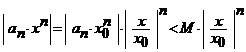 .
.
Urmeaza ca seria ![]() este convergenta
pentru toate valorile lui
este convergenta
pentru toate valorile lui ![]() situate in interiorul
intervalului
situate in interiorul
intervalului ![]() fiind majorata de
seria geometrica
convergenta cu ratia subunitara
fiind majorata de
seria geometrica
convergenta cu ratia subunitara ![]() . Sa consideram multimea
de convergenta, adica multimea
. Sa consideram multimea
de convergenta, adica multimea ![]() } cu proprietatea ca seria de puteri (3.1) este absolut convergenta. Aceasta
multime este marginita superior de numarul real pozitiv
} cu proprietatea ca seria de puteri (3.1) este absolut convergenta. Aceasta
multime este marginita superior de numarul real pozitiv ![]() , eventual
, eventual ![]() . Daca
. Daca ![]() atunci seria de puteri
este absolut convergenta in orice
atunci seria de puteri
este absolut convergenta in orice ![]() cu
cu ![]() (din definitia
marginii superioare exista
(din definitia
marginii superioare exista ![]() a.i.
a.i. ![]() ) deci, seria de puteri converge, in intervalul
) deci, seria de puteri converge, in intervalul ![]() , catre o functie
, catre o functie ![]() si vom scrie
si vom scrie
![]() . (5)
. (5)
ii). Daca seria este divergenta in ![]() atunci, pentru orice
atunci, pentru orice ![]() , cu
, cu ![]() , seria este divergenta. In consecinta, pentru
, seria este divergenta. In consecinta, pentru
![]() seria de puteri este
divergenta.
seria de puteri este
divergenta.
Asadar, seria ![]() converge absolut
pentru orice
converge absolut
pentru orice ![]() cu
cu ![]() si este
divergenta pentru valorile lui
si este
divergenta pentru valorile lui ![]() cu
cu ![]() .
.
Intervalul ![]() se numeste interval de convergenta, iar
numarul
se numeste interval de convergenta, iar
numarul ![]() se numeste raza de convergenta a seriei
de puteri date.
se numeste raza de convergenta a seriei
de puteri date.
In punctele ![]() , seria de puteri poate fi convergenta sau
divergenta. In aceste puncte convergenta seriei se studiaza
separat.
, seria de puteri poate fi convergenta sau
divergenta. In aceste puncte convergenta seriei se studiaza
separat.
40. Observatie.
Daca nu exista alte puncte de convergenta decat ![]() atunci
atunci ![]() . De exemplu, seria de puteri
. De exemplu, seria de puteri![]() , asa cum rezulta din criteriul raportului, este divergenta
, asa cum rezulta din criteriul raportului, este divergenta
![]() .
.
Exemple
Seria de puteri
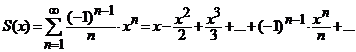 , (6)
, (6)
are raza de convergenta ![]() . Deci, este absolut convergenta pentru orice
. Deci, este absolut convergenta pentru orice ![]() .
.
Intr-adevar, pentru ![]() , fixat, din criteriul raportului pentru serii numerice,
obtinem
, fixat, din criteriul raportului pentru serii numerice,
obtinem
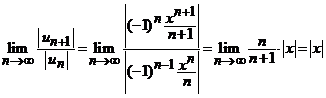 .
.
Daca ![]() atunci seria este
convergenta si daca
atunci seria este
convergenta si daca ![]() seria este
divergenta.
seria este
divergenta.
Pentru ![]() , avem
, avem ![]() , care este convergenta (din criteriul lui Leibniz).
, care este convergenta (din criteriul lui Leibniz).
Pentru ![]() , avem
, avem ![]() , care este divergenta.
, care este divergenta.
Asadar, seria este convergenta
pentru orice ![]() .
.
41. Observatie.
Asa cum se stie, seria de puteri considerata este tocmai seria
Taylor asociata functiei ![]() , dezvoltata dupa puterile lui
, dezvoltata dupa puterile lui ![]() . In consecinta,
. In consecinta, ![]() .
.
Vom observa ca desi ![]() exista,
totusi
exista,
totusi ![]() nu exista.
nu exista.
Seria de puteri
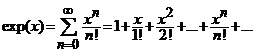 , (7)
, (7)
are raza de convergenta ![]() si in
consecinta, este convergenta pentru orice
si in
consecinta, este convergenta pentru orice ![]() .
.
Intr-adevar, pentru ![]() , dar fixat, din criteriul raportului pentru serii numerice,
obtinem
, dar fixat, din criteriul raportului pentru serii numerice,
obtinem
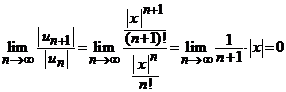 , oricare ar fi
, oricare ar fi ![]() .
.
. Seria de puteri
![]() , (8)
, (8)
este convergenta pentru orice ![]() .
.
Seria de puteri coincide cu seria Taylor
asociata functiei ![]() , dezvoltata dupa puterile lui
, dezvoltata dupa puterile lui ![]() . Deci, pentru
. Deci, pentru ![]() seria este
convergenta si are suma
seria este
convergenta si are suma ![]() .
.
Pentru ![]() deducem
deducem ![]() si in
consecinta, seria este divergenta.
si in
consecinta, seria este divergenta.
Pentru ![]() , desi
, desi ![]() totusi, seria
totusi, seria ![]() .este divergenta.
.este divergenta.
Calculul razei de convergenta a seriilor de puteri cu ajutorul coeficientiilor (Cauchy 1821 si ulterior, Hadamard).
42.
Teorema Cauchy-Hadamard. (i). Daca exista limita
superioara 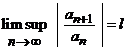 , atunci raza de
convergenta a seriei are valoarea
, atunci raza de
convergenta a seriei are valoarea ![]() (din criteriul
raportului pentru serii numerice).
(din criteriul
raportului pentru serii numerice).
(ii).
Daca exista ![]() , atunci raza de
convergenta R este
egala cu
, atunci raza de
convergenta R este
egala cu ![]() (din criteriul
radacinii pentru serii numerice).
(din criteriul
radacinii pentru serii numerice).
Deci,
raza de convergenta a seriei de puteri ![]() se calculeaza cu
una din formulele
se calculeaza cu
una din formulele
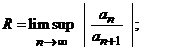
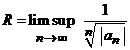 . (9)
. (9)
Daca ![]() atunci se ia
atunci se ia ![]() , iar daca
, iar daca ![]() atunci
atunci ![]() .
.
Se pot considrea serii de puteri avand forma
(ordonate dupa puterile binomului ![]() )
)
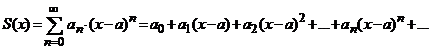 .. (10)
.. (10)
Atunci, folosind translatia
![]() , rezultatele stabilite mai sus se aplica seriei de
puteri
, rezultatele stabilite mai sus se aplica seriei de
puteri ![]() , care este absolut convergenta in intervalul de
convergenta
, care este absolut convergenta in intervalul de
convergenta ![]() si
divergenta in punctele
si
divergenta in punctele ![]() cu
cu ![]() .
.
43.
Definitie. Spunem
ca functia ![]() este reprezentabila printr-o serie de puteri in
este reprezentabila printr-o serie de puteri in ![]() daca pentru orice
daca pentru orice
![]() exista o
vecinatate de forma
exista o
vecinatate de forma ![]() si o serie de
puteri de forma (10) care converge absolut si uniform la
si o serie de
puteri de forma (10) care converge absolut si uniform la ![]() pentru orice
pentru orice ![]() .
.
In acest caz, scriem
![]() si
si ![]() .
.
Mai mult, functia ![]() este indefinit
derivabila pe
este indefinit
derivabila pe ![]() (adica,
(adica, ![]() ) si avem
) si avem
![]() (11)
(11)
Seria de puteri
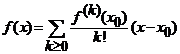 , (12)
, (12)
se numeste seria Taylor
asociata functiei ![]() pe
pe ![]() .
.
Intr-adevar, inlocuind in seria de
puteri pe ![]() cu
cu ![]() obtinem
obtinem ![]() . Deci seria de puteri, se scrie
. Deci seria de puteri, se scrie
![]() .
.
Impartind aceasta relatie
la ![]() si apoi din
relatia obtinuta prin trecere la limita, cand
si apoi din
relatia obtinuta prin trecere la limita, cand ![]() , rezulta
, rezulta
![]() .
.
Deci exista ![]() . Deoarece, seria de puteri
. Deoarece, seria de puteri ![]() este uniform
convergenta oricare ar fi
este uniform
convergenta oricare ar fi ![]() , atunci si seria de puteri
, atunci si seria de puteri ![]() este uniform
convergenta (!) oricare ar fi
este uniform
convergenta (!) oricare ar fi ![]() si avem
si avem ![]() . Procedand ca mai sus, obtinem
. Procedand ca mai sus, obtinem
![]() .
.
44. In continuare vom studia unele proprietati ale seriilor de puteri:
Seria de puteri (4) converge absolut si uniform in intervalul ![]() pentru orice
pentru orice ![]() si este
divergenta daca
si este
divergenta daca ![]() .
.
Intr-adevar, deoarece ![]() , daca alegem
, daca alegem ![]() atunci seria
numerica
atunci seria
numerica ![]() este convergenta.
Pentru orice
este convergenta.
Pentru orice ![]() cu
cu ![]() , termenii seriei de puteri (4) raman majorati in
modul de termenii acestei serii numerice convergente si, din criteriul lui
Weierstrass, rezulta ca seria de puteri este uniform
convergenta, desigur pentru
, termenii seriei de puteri (4) raman majorati in
modul de termenii acestei serii numerice convergente si, din criteriul lui
Weierstrass, rezulta ca seria de puteri este uniform
convergenta, desigur pentru ![]() , catre o functie
, catre o functie ![]() si scriem
si scriem ![]() .
.
Fie seria de puteri ![]() , convergenta pentru
, convergenta pentru ![]() , unde
, unde ![]() . Atunci suma sa defineste, pe multimea de
convergenta, o functie
continua,
. Atunci suma sa defineste, pe multimea de
convergenta, o functie
continua, ![]() si scriem
si scriem
![]() . (13)
. (13)
Intr-adevar, pentru orice ![]() fixat, exista
fixat, exista ![]() a.i.
a.i. ![]() . Deoarece seria de puteri este uniform convergenta pe
. Deoarece seria de puteri este uniform convergenta pe ![]() , atunci suma sa este functie continua pe acest
interval, deci si in punctul
, atunci suma sa este functie continua pe acest
interval, deci si in punctul ![]() .
.
Asadar, suma ![]() a seriei de puteri (4),
pentru orice
a seriei de puteri (4),
pentru orice ![]() situat in intervalul
de convergenta, este functie
continua de variabila
situat in intervalul
de convergenta, este functie
continua de variabila ![]() .
.
(Identitatea seriilor de puteri). Fie seriile convergente ![]() si
si ![]() avand razele de
convergenta
avand razele de
convergenta ![]() respectiv
respectiv ![]() . Daca exista
. Daca exista ![]() astfel incat
astfel incat ![]() cu
cu ![]() sa avem egalitatea
sa avem egalitatea
![]() (adica, cele
doua serii au aceeasi suma in
(adica, cele
doua serii au aceeasi suma in ![]() ) atunci pentru orice
) atunci pentru orice ![]() , aceste serii sunt identice si scriem
, aceste serii sunt identice si scriem
![]() , (adica
, (adica ![]() ).
).
In adevar, deoarece ![]() in
in ![]() rezulta ca
rezulta ca ![]() pentru orice
pentru orice ![]() cu
cu ![]() si deci
si deci ![]() de unde obtinem
de unde obtinem ![]() . De aici rezulta
. De aici rezulta
![]() .
.
45. Observatie. Proprietatea (3), care stabileste unicitatea
dezvoltarii unei functii in serie de puteri, are multiple
aplicatii. De exemplu, daca o functie este para
(impara) atunci ea se dezvolta intr-o serie de puteri de forma (4)
care contine numai puterile pare (impare) ale lui ![]() .
.
4 Operatii algebrice cu serii de puteri
Fie seriile de puteri 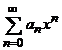 si
si 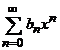 , avand razele de
convergenta respectiv
, avand razele de
convergenta respectiv ![]() si
si ![]() . Atunci,
. Atunci,
(a).
Seria suma 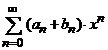 are raza de convergenta R care satisface una din relatiile
are raza de convergenta R care satisface una din relatiile
![]() , daca
, daca ![]() sau
sau![]() , daca
, daca ![]() . (14)
. (14)
si pentru orice ![]() cu
cu ![]() are loc egalitatea
are loc egalitatea
![]() (unde
(unde ![]() ). (15)
). (15)
(b).
Pentru orice scalar ![]() , seria
, seria 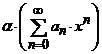 are raza de convergenta egala
cu
are raza de convergenta egala
cu ![]() .
.
(c).
Seria produs ![]() , are raza de convergenta egala cu
, are raza de convergenta egala cu ![]() care satisface
conditia
care satisface
conditia ![]() si egalitatea
si egalitatea
![]() , (16)
, (16)
poate fi scrisa numai pentru ![]() , cu
, cu ![]() .
.
47.
Teorema. Fie ![]() o serie de puteri
si fie
o serie de puteri
si fie ![]() raza sa de
convergenta. Atunci
raza sa de
convergenta. Atunci
(1). Seria de puteri converge absolut si
uniform in orice ![]() cu
cu ![]() .
.
(2). Suma ![]() a seriei de puteri este functie continua in
interiorul intervalului de convergenta, deci in multimea
a seriei de puteri este functie continua in
interiorul intervalului de convergenta, deci in multimea ![]() .
.
(3). Daca raza de convergenta
a seriei de puteri este nenula (![]() ) atunci seria de puteri se poate deriva termen cu termen in
) atunci seria de puteri se poate deriva termen cu termen in ![]() si seria
derivatelor are aceeasi raza de convergenta R.
si seria
derivatelor are aceeasi raza de convergenta R.
Mai mult, are loc egalitatea (seria de puteri se poate deriva termen cu termen in tot intervalul de convergenta)
![]() , oricare ar fi
, oricare ar fi ![]() cu
cu ![]() . (17)
. (17)
48. Observatie. Aceasta teorema face posibila derivarea termen cu termen a seriei de puteri in tot intervalul sau de convergenta. Adica
![]() .
.
Fie seria de puteri
![]() , convergenta in
, convergenta in ![]() .
.
Potrivit teoremei 45, functia ![]() are in interiorul
intervalului de convergenta derivate de orice ordin. Scriind
derivatele succesive obtinem, in intervalul de convergenta,
seriile de puteri convergente:
are in interiorul
intervalului de convergenta derivate de orice ordin. Scriind
derivatele succesive obtinem, in intervalul de convergenta,
seriile de puteri convergente:
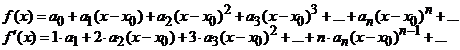
![]()
![]()
Daca alegem ![]() , din aceste egalitati deducem expresiile cunoscute
ale coeficientilor
, din aceste egalitati deducem expresiile cunoscute
ale coeficientilor ![]() ai seriei de puteri:
ai seriei de puteri: ![]() iar seria de puteri
iar seria de puteri 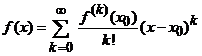 ,
,
reprezinta
tocmai seria Taylor pentru
functia f(x) dezvoltata dupa
puterile lui ![]() .
.
Demonstratie. Primele doua afirmatii din teorema au fost deja demonstrate mai inainte.
(3). Notam, ca mai sus, cu ![]() termenii seriei de
puteri. Atunci functiile
termenii seriei de
puteri. Atunci functiile ![]() sunt continue si
derivabile pentru orice
sunt continue si
derivabile pentru orice ![]() si au derivatele
egale cu:
si au derivatele
egale cu:
![]() ,
, ![]()
Fie ![]() oarecare, fixat cu
oarecare, fixat cu ![]() . Atunci exista
. Atunci exista ![]() a.i.
a.i. ![]() . Deoarece seria numerica
. Deoarece seria numerica
![]() este convergenta
atunci termenul ei general este marginit. Deci exista
este convergenta
atunci termenul ei general este marginit. Deci exista ![]() a.i.
a.i.
![]() ,
, ![]()
Atunci, pentru termenul general al seriei derivate obtinem majorarea
![]()
Deoarece seria
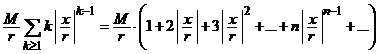 ,
,
este
convergenta (pentru ca ![]() ) atunci seria (3.11) este absolut convergenta.
Asadar, aceasta serie este uniform convergenta in
) atunci seria (3.11) este absolut convergenta.
Asadar, aceasta serie este uniform convergenta in ![]() catre
functia
catre
functia ![]() . Afirmatia ca
. Afirmatia ca ![]() rezulta din
urmatoarea
rezulta din
urmatoarea
49. Observatia.
Daca ![]() este o serie de puteri
convergenta in
este o serie de puteri
convergenta in ![]() atunci
atunci ![]() . In adevar, fie
. In adevar, fie ![]() cu
cu ![]() . Atunci pentru
. Atunci pentru ![]() avem
avem
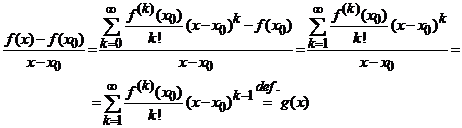
Deoarece functia g(x) este continua
in intervalul de convergenta si din ultima egalitate deducem 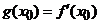 , atunci obtinem
, atunci obtinem
![]() .
.
50. Observatia.
Functia ![]() , care reprezinta suma unei serii de puteri in
intervalul de convergenta, este de clasa
, care reprezinta suma unei serii de puteri in
intervalul de convergenta, este de clasa ![]() in interiorul acestui
interval si seria de puteri reprezinta tocmai o serie Taylor.
in interiorul acestui
interval si seria de puteri reprezinta tocmai o serie Taylor.
51.
Teorema. Fie ![]() o serie de puteri
si fie
o serie de puteri
si fie ![]() raza sa de
convergenta. Atunci aceasta se poate integra termen cu termen in
intervalul
raza sa de
convergenta. Atunci aceasta se poate integra termen cu termen in
intervalul ![]() , unde
, unde ![]() si avem
si avem
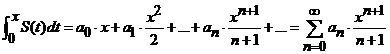 ,
, ![]() cu
cu ![]() . (18)
. (18)
Asadar, seria de puteri data si seria de puteri (18) au aceeasi multime de convergenta.
52. Observatie.
Valoarea lui ![]() poate sa
coincida cu una dintre extremitatile intervalului de
convergenta, daca seria de puteri
poate sa
coincida cu una dintre extremitatile intervalului de
convergenta, daca seria de puteri ![]() este convergenta cand
este convergenta cand ![]() ia aceasta
valoare.
ia aceasta
valoare.
Demonstratie. Deoarece functiile ![]() sunt continue pe orice interval
sunt continue pe orice interval ![]() , unde
, unde ![]() , atunci ele sunt integrabile pe
, atunci ele sunt integrabile pe ![]() . Seria de puteri fiind uniform convergenta pe
multimea
. Seria de puteri fiind uniform convergenta pe
multimea ![]() , atunci suma sa
, atunci suma sa ![]() este continua
si deci integrabila pe orice interval
este continua
si deci integrabila pe orice interval ![]() cu
cu ![]() .
.
Fie 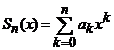 sirul sumelor
partiale asociat seriei de puteri. Atunci, putem scrie
sirul sumelor
partiale asociat seriei de puteri. Atunci, putem scrie
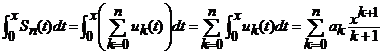 .
.
Deoarece ![]() atunci, din extimarea
atunci, din extimarea
![]() ,
,
cand ![]() , deducem ca seria de puteri poate fi integrata
termen cu termen si are loc formula (3.12).
, deducem ca seria de puteri poate fi integrata
termen cu termen si are loc formula (3.12).
53. Observatie. Teoremele 47 si 51 conduc la concluziile:
(i).
Seria ![]() este absolut si uniform convergenta
pe orice interval
este absolut si uniform convergenta
pe orice interval ![]() si
si ![]() este derivata
functiei
este derivata
functiei ![]() in interiorul
intervalului de convergenta.
in interiorul
intervalului de convergenta.
(ii). Seria 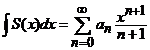 este absolut si uniform convergenta
pe orice interval
este absolut si uniform convergenta
pe orice interval ![]() si
si ![]() este primitiva
functiei
este primitiva
functiei ![]() in intervalul de
convergenta.
in intervalul de
convergenta.
Exercitiul 1. Sa se determine seria de puteri (seria Taylor in jurul lui zero) a functiei
![]() .
.
Solutie. Functia ![]() este derivabila
pe
este derivabila
pe ![]() si avem
si avem ![]() . Seria de puteri crespunzatoare functiei
. Seria de puteri crespunzatoare functiei ![]() are forma
are forma
![]() , pentru
, pentru ![]() .
.
Integrand termen cu termen aceasta serie de puteri obtinem seria
![]() , pentru orice
, pentru orice ![]() , cu
, cu ![]() .
.
Daca alegem ![]() atunci constanta de
integrare
atunci constanta de
integrare ![]() are valoarea
egala cu zero si obtinem seria de puteri
are valoarea
egala cu zero si obtinem seria de puteri
![]() , pentru orice
, pentru orice ![]() , cu
, cu ![]() . (19)
. (19)
Deoarece seria numerica ![]() este convergenta
(vezi criteriul lui Leibniz) atunci, luand
este convergenta
(vezi criteriul lui Leibniz) atunci, luand ![]() , din (19) gasim suma acestei serii numerice:
, din (19) gasim suma acestei serii numerice:
![]() (20)
(20)
Cum functia ![]() este impara
observam ca seria de puteri (19) contine numai puterile impare
ale lui
este impara
observam ca seria de puteri (19) contine numai puterile impare
ale lui ![]() si in plus
deducem ca seria (20) este convergenta chiar pe intervalul inchis
si in plus
deducem ca seria (20) este convergenta chiar pe intervalul inchis ![]() .
.
Exercitiul
2. Fie seria de puteri 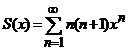 . Se cere:
. Se cere:
(a). Sa se determine multimea de convergenta a seriei.
(b). Sa se calculeze suma ![]() .
.
Solutie. (a). Fie ![]() ,
, ![]() coeficientii seriei de puteri. Din formula (9)1
avem
coeficientii seriei de puteri. Din formula (9)1
avem
![]() .
.
Deci seria de puteri are raza de
convergenta egala cu unitatea. Se verifica, fara
dificultate, ca pentru ![]() seria este
divergenta. Asadar, seria de puteri este convergenta pentru
seria este
divergenta. Asadar, seria de puteri este convergenta pentru ![]() .
.
(b). Pe multimea de convergenta, seria de puteri se poate integra termen cu termen si avem
![]() , pentru orice
, pentru orice ![]() .
.
Deci, 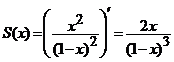 , oricare ar fi
, oricare ar fi ![]() .
.
52. Observatie. Pentru calcului sumei de mai sus am folosit seria geometrica
![]() (*)
(*)
si seria de puteri obtinuta prin derivarea termen cu termen a seriei (*),
![]() . (**)
. (**)
Inmultind relatia (**) cu ![]() obtinem seria de
puteri
obtinem seria de
puteri
![]() , cu
, cu ![]() .
.
Exercitiul
3. Seria de puteri 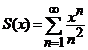 are raza de
convergenta
are raza de
convergenta ![]() . Deci seria este absolut convergenta in
. Deci seria este absolut convergenta in ![]() . Pentru
. Pentru ![]() seria este
convergenta .
seria este
convergenta .
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |