Elementele introduse nu permit studierea unor aspecte ale spatiilor vectoriale legate de notiunile de unghi si de distanta. Aceasta se poate face inzestrand spatiul vectorial cu un tip de produs numit produs scalar.
DEFINITIA 1. Fie K = C , R si V un K - spatiu vectorial. O aplicatie ( · | · ): V× V K se numeste produs scalar daca:
i) aplicatia
![]() este liniara
este liniara ![]() ,
,
ii) ![]() , (daca K
= R , atunci
, (daca K
= R , atunci ![]() ), adica
), adica
(![]() |
|![]() )
)![]() (
(![]() |
|![]() )
)![]() (
(![]() |
|![]() ),
),
iii) ![]() .
.
Notatii ![]()
Observatii 1. ![]() .
.
Intr - adevar, ![]() , deci
, deci ![]() .
.
![]()
care este imediata din Definitia 1.2.1 iii) si Observatia 1.2.1![]() .
.
![]() C,
C,![]()
Intr-adevar ![]()
![]()
Exemple. 1. Fie K = C si V = Kn =![]() K,
K, ![]() .
.
Pentru orice ![]() Kn si
Kn si ![]() Kn punem
Kn punem
![]()
Daca K = R avem
![]()
In
spatiul
vectorial ![]() al functiilor
continue pe intervalul
al functiilor
continue pe intervalul
[a, b] ![]() R, produsul scalar este
R, produsul scalar este
![]()
DEFINITIA 1. Un spatiu vectorial pe care s-a definit un produs scalar se numeste spatiu vectorial euclidian.
TEOREMA 1.2.1 (Inegalitatea lui Schwarz sau inegalitatea lui Cauchy - Buneakovski)
![]() . (1.2.1)
. (1.2.1)
Demonstratie. Folosind Observatia
1.2.1![]() ) si proprietatea i) din Definitia 1.2.1, avem
) si proprietatea i) din Definitia 1.2.1, avem
![]()
![]() C.
C.
In particular, pentru ![]() cu
cu ![]() , inegalitatea de mai sus devine
, inegalitatea de mai sus devine
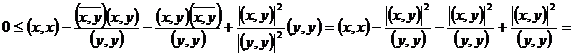
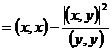 .
.
Deci
![]()
DEFINITIA 1. Fie K = C, R si V un K - spatiu vectorial. O aplicatie ║
∙║![]() R se numeste norma daca
R se numeste norma daca
(i) ![]() ,
,
(ii) ![]() K si
K si ![]() (omogenitate),
(omogenitate),
(iii) ![]() ,
, ![]() ( inegalitatea
triunghiului).
( inegalitatea
triunghiului).
Observatia
1. ![]()
Intradevar, folosind proprietatile (i), (ii), (iii) obtinem
![]()
deci
![]()
DEFINITIA
1. Perechea ![]() se numeste spatiu normat.
se numeste spatiu normat.
TEOREMA 1.2.2 Orice produs scalar determina o norma prin egalitatea
![]()
Demonstratie. Verificam cele trei axiome din Definitia 1.2.3 :
![]() (conform axiomei
(iii) din Def. 1.2.1).
(conform axiomei
(iii) din Def. 1.2.1).
![]()
![]()
![]()
![]() .
.
Deci
![]()
si folosind inegalitatea lui Schwarz obtinem
![]()
Prin urmare
![]()
Exemple de norme pe Kn
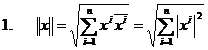 ( K=C
) ;
( K=C
) ;
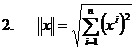 ( K=R
) ;
( K=R
) ;
![]() ;
;
![]() .
.
Precizari. 1. Norma lui ![]() se mai numeste
si lungimea
vectorului
se mai numeste
si lungimea
vectorului ![]() .
.
2. Norma din exemplul 1 (sau 2) se numeste norma euclidiana pe Kn.
Cu ajutorul normei se poate da urmatoarea definitie:
DEFINITIA 1.2.5 Fie
En un spatiu
vectorial euclidian de dimensiune n. Un vector ![]() , cu proprietatea ca
, cu proprietatea ca
![]() , se numeste vector unitate sau versor
, se numeste vector unitate sau versor
Observatii 1. 1. Cu aceasta notiune, pentru ![]() , avem
, avem
![]() .
.
2. Cu ajutorul normei, inegalitatea Cauchy - Schwarz se mai scrie
![]() (1.2.1')
(1.2.1')
sau, daca ![]() ,
, ![]() ,
,
![]() . (1.2.1")
. (1.2.1")
DEFINITIA 1. Se numeste unghi
neorientat al vectorilor x si y numarul ![]() dat de relatia
dat de relatia
![]()
DEFINITIA 1.2.7 Fie ![]() . Se numeste metrica sau distanta o functie d: En×En
. Se numeste metrica sau distanta o functie d: En×En ![]() R care are proprietatile:
R care are proprietatile:
D1. ![]() (pozitivitate);
(pozitivitate);
D2. ![]() (simetrie);
(simetrie);
D3. ![]() (inegalitatea triunghiului).
(inegalitatea triunghiului).
DEFINITIA 1. Un spatiu vectorial inzestrat cu o distanta se numeste spatiu metric.
DEFINITIA 1. Distanta definita cu ajutorul normei euclidiene se numeste distanta euclidiana.
TEOREMA 1.2.3 Fie ![]() normat cu norma euclidiana.
Functia
reala
normat cu norma euclidiana.
Functia
reala
![]() R definita prin
R definita prin
![]()
este o distanta (metrica) pe En.
Demonstratie. Evidenta prin verificarea axiomelor din Definitia 1.2.7.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |