TRANSFORMARI LINIARE

TRANSFORMARI LINIARE

1 Definitie. Proprietati generale. Operatii

Indisolubil legata de notiunea de spatiu vectorial este notiunea de transformare liniara de spatii vectoriale.

DEFINITIA Fie U si V doua K - spatii vectoriale. O aplicatie F : U V se numeste K-liniara (sau mai simplu liniara, atunci cand corpul K este subinteles) daca:

F ( ) =F ( ) +F ( ), I U (F este aditiva) ,

F ( ) = F ( ), I U, I K (F este omogena) .

Conditiile din definitia 3.1 sunt echivalente cu conditia

PROPRIETATEA O aplicatie F : U V este o transformare liniara daca si numai daca

F ( ) = F ( ) + F ( ) , I K, I U.

Demonstratie. Presupunem caF este transformare liniara. Din Definitia 1 rezulta

F ( ) =F ( ) +F ( ) = F ( ) + F ( ) .

Reciproc, daca F satisface conditia (3) punand 1_K , deducem

F ( ) =F ( ) +F ( ) , care este tocmai relatia (1) si, punand apoi , rezulta F ( ) = F ( ) , adica relatia (2), ceea ce arata ca aplicatia F este liniara.

Notatie. L (U, V) : = = Hom(U, V)

DENUMIRI. Vectorul F ( ) I V, pentru I U, se numeste imaginea lui prin F, iar I U, a carui imagine este F ( ) I V, se numeste preimaginea lui F ( ).

Cazuri particulare. Daca F IL (U, V) si

F injectiva atunci F se numeste monomorfism;

F surjectiva atunci F se numeste epimorfism;

F bijectiva atunci F se numeste izomorfism.

Daca F I L (U, U) T F se numeste endomorfism.

Daca F I L (U, U) bijectiva T F se numeste automorfism.

Daca F ( U / K,K) T F se numeste forma liniara.

Exemple. 1. Produsul scalar in E_n cu unul din vectori fixati este o forma liniara.

3. Fie R_n[X] spatiul vectorial al polinoamelor de grad cel mult n si F : R_n[X] R_n-1[X] aplicatia care asociaza fiecarui polinom derivata lui, adica

.

Aceasta aplicatie este liniara deoarece I R[X] si I R, avem

F( ( ) + ( )) = ( ( ) + ( )) = ( ) + ( )=

= F ( ) + F ( ).

4. Fie V un spatiu vectorial peste campul K, un element fixat din K si aplicatia F : V V definita prin F , I V. Transformarea F este liniara deoarece, I V si I K, avem

F F F .

Aplicatia F se numeste omotetia spatiului V de raport I K

Luand , obtinem transformarea liniara care asociaza fiecarui vector I V opusul sau . Aceasta se numeste simetria lui V fata de subspatiul nul.

TEOREMA Daca F I L (U, V) atunci:

F (0_U) = 0_V

U₁ / K U / K T F (U₁) / K V / K;

V₁ / K V / K T F^{- -1} (V₁) / K U / K;

S = _i=1n,

F bijectiva T F^{- -1} I F (V, U).

Demonstratie. 1. Din (1) pentru si apoi TF (0_U) = 0_V .

U₁ / K U / K din definitie T [ I K si I U₁ T I U₁] T F ( ) IF (U₁) si F ( ) = F ( ) + F ( ) IF (U₁) . Deci

I K si F ( ),F ( ) IF (U₁) T F ( ) + F ( ) IF ( U₁) T

F ( U₁) / K V / K.

Fie IF^{- -1} (V₁) si I K. Atunci F ( ),F ( ) I V₁, deci (F fiind liniara si V₁ fiind subspatiu), avem

F ( ) = F ( ) + F ( ) I V₁ ,

de unde

IF^{- -1} (V₁) .

.

Deci F F F si astfel incat F (S).

Pentru astfel incat F ( sau F ^-1 ). Analog, pentru astfel incat F ( sau F ^-1 ). Avem

F ^-1 F ^-1 F + F F ^-1(F
F ^-1 + F ^-1 , K,

deci F ^-1IL (V, U). 

DEFINITIA Fie L (U, V) pe care introducem urmatoarele:

1. egalitatea F F I L (U, V), F F ₂ F ₁( ) = F ₂( ), I U;

2. adunarea F ₁, F ₂ I L (U, V), F := F F F ( ) = F ₁( ) + F ₂( ), IU;

3. inmultirea cu scalari F I L (U, V), I K, F : = F F ( )= F ₁( ), I U.

PROPRIETATI

1. (L (U, V),+) formeaza grup comutativ;

2. L (U, V) impreuna cu adunarea si inmultirea cu scalari formeaza spatiu vectorial peste K .

Demonstratie. Evidenta, prin verificarea axiomelor din definitiile corespunzatoare.

TEOREMA Fie E si E doua K spatii vectoriale, B = (e₁, e₂, , e_n) baza in E si C = un sistem arbitrar de vectori din E . Atunci exista o aplicatie liniara unica F : E E cu proprietatea ca F (e_k) = v_k, k = 1, 2, , n.

Demonstratie. B este baza in E, deci orice I E este o combinatie liniara de vectorii multimii B, adica

cu unic determinati.

Definim aplicatia F : E E prin

F

si vom arata ca F este liniara si ca F , .

Fie si vectori arbitrari din E, K scalari arbitrari si consideram combinatia liniara

.

Tinand seama de modul cum a fost definita aplicatia F , avem pe rand

F F F

si, conform cu proprietatea 1, aplicatia F este liniara. Tot din definitia lui F , pentru

si , pentru , deci F , .

Sa demonstram unicitatea. Fie GIL ( E, E ) cu proprietatea ca G , .

Pentru orice , din E avem G G .

Valorile lui G coincid cu valorile lui F I E, deci G F . Aplicatia F , definita mai sus, este singura aplicatie liniara care ia valorile date F , .

Retinem din aceasta demonstratie urmatoarea expresie pentru imaginea lui prin aplicatia F

F F F F F

= F F F

si facand notatia (F ( ),F ( ), , F ( )) : = F (B) obtinem urmatoarea consecinta:

Consecinta Daca F I L (E, E ) si B este baza a lui E, atunci pentru I E avem

F ( ) = F (B) [ ]_B .

Consecinta 2 Daca ind_E C si F I L (E, E ), cu C F , pentru B - baza, atunci F este monomorfism.

Demonstratie. Fie IE, cu F ( ) = F ( ) F (B)[ ]_B = F (B)[ ]_B T

F (B)([ ]_B - [ ]_B) = 0_E si ind_E C = ind_E F (B) T [ ]_B = [ ]_B T B[ ]_B = B[ ]_B T TF injectiva.

TEOREMA Daca F I L (U_n, V) monomorfism si

daca S = _i=1,,n , cu ind_UnS T ind_V F (S);

daca B = (e₁, e₂, ,e_n) este baza a lui U_n T ind_V F (B);

daca dimU_n = dimV = n si B este baza a lui U_n T F (B) baza a lui V.

Demonstratie 1.

F monomorfismT F F F T F F T ind_V F (S)

si 3. rezulta din 1.

DEFINITIA Fie F ₁ I L (U, V) si F ₂ I L (V, W), atunci F : U W prin F ( ) = (F ₂ F ₁)( ), I U se numeste compunerea sau produsul transformarilor liniare si se noteaza F F ₂ F ₁ sau F F ₂ F ₁.

PROPRIETATI

Produsul transformarilor liniare este o transformare liniara.

Produsul este asociativ si in general nu este comutativ.

Compunerea este distributiva la dreapta si la stanga in raport cu adunarea.

Demonstratie. (evidenta) exercitiu.

In L (V, V) se pot introduce:

- transformarea identica I : V V prin I ( ) = , I V;

- puterile naturale ale unei transformari:F = I , F =F F .

2 Nucleul si imaginea unei transformari liniare

DEFINITII 4. 1. Fie F I L (U,V). Se numeste nucleu al transformarii liniare F multimea

= F (0_v):=Ker (F

adica multimea preimaginilor lui 0_v .

2. Se numeste imagine a transformarii liniare multimea

= F (U) :=Im(F

adica multimea imaginilor lui U.

TEOREMA 4. Daca F I L (U,V) atunci Ker(F )/K U /K si Im F /K V /K.

Demonstratie. Evidenta din proprietatile 3. si respectiv 2. ale teoremei 1.

TEOREMA 5. Daca U si V sunt K-spatii finit dimensionale si F I L ( U,V ) atunci

dim Ker (F ) + dim Im (F ) = dim U

Demonstratie. Fie ( ) o baza a lui Ker(F ) si ( ) o baza a lui Im(F ). Atunci

F ( ) = 0_v ,

si exista I U astfel incat

F ( ) , .

Sa aratam ca este o baza a lui U. Fie I K, , si sa consideram

,

unde, tinand seama de (6) si (7), obtinem

F F F

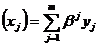
si, cum , , , prin urmare (8) devine

Cu rezulta , . Asadar, obtinem

.

Sa aratam acum ca U=L(). Pentru orice IU avem   F ( )I Im(F ) si multimea = fiind baza pentru Im(F ), rezulta ca exista I K , astfel incat

F F ,

deci  F ,

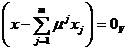
adica  ( F

Cum ( ) este baza pentru Ker (F ), exista I K cu proprietatea ,

deci  .

Asadar, U = L ().

DEFINITIA dim Ker(F ) si dim Im(F ) se numesc defectul si, respectiv, rangul tranformarii liniare F

TEOREMA 6 Daca F I L (U ,V) atunci urmatoarele afirmatii sunt echivalente: (a) F monomorfism (b) Ker (F

Demonstratie. (b) T (a) Din F ( ) = F ( ) si F liniara T F ( ) = 0_v T

( F ) F injectiva .

Ker(F ) . Din Ker(F T F si cum F T

(a) T (b) T F F si F injectiva T .

( F ), evidenta pentru ca Ker(F )/K U /K (conf. T 4)

3 Matrice asociata unei transformari liniare

Fie E si E' doua K-spatii vectoriale si B=( ) o baza in E. Conform cu T.2, o transformare liniara F I L (E,E') este complet determinata daca sunt date valorile F ( )= I E', .

Fie B'= ( ) o baza in E'. Cei n vectori pot fi dati prin coordonatele lor in raport cu baza B' , adica

(9) .

Construim un tablou cu coordonatele acestor vectori in care coordonatele vectorului se gasesc pe coloana , in ordine naturala. Matricea corespunzatoare acestui tablou o notam M(F ; B,B').

	F  (e1)	F  (e2)	. .	F  (ej)	. .	F  (en)
(10)   u1	a	a	. .	a1j	. .	a1n
u2	a	a	. .	a2j	. .	a2n
up	ap1	ap2	. .	apj	. .	apn

M(F ; .

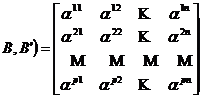
DEFINITIA Fie F I L (E, E' ), B = (e₁,e₂,,e_n) o baza in E si

B'=(u₁, u₂,,u_p) o baza in E'. Matricea M(F ; B,B') ale carei coloane sunt formate cu coordonatele vectorilor F (e_j ) in raport cu B', se numeste matricea transformarii F in raport cu perechea de baze (B,B').

Pentru un endomorfism F I L (E,E') se foloseste notatia mai simpla M(F ; B).

Observatia Matricea M(F ; B,B')IM( ,K) are numarul de linii =cardB'=dim E' si numarul de coloane =card B=dim E, iar elementele sale sunt din corpul K. Deoarece, conform T.2., exista o aplicatie liniara unica F I L (E,E') cu valorile F ( )= date, aplicatia

M( ; B,B') : L (E,E') M( ,K)

avand valorile M(F ; B,B') definite mai sus, este o bijectie (deci pentru oricare transformare F matricea M(F ; B,B') exista si este unic determinata).

TEOREMA 7 Fie F I L (E,E'), B=(e₁,e₂,,e_n) o baza in E, B'=(u₁, u₂,, u_n) o baza in E', M(F ; B,B') matricea transformarii si doi vectori I E, I E' de forma

Atunci are loc echivalenta: f ( ) = M(F ;B,B )[ ]_B = [F ( )]_B.

Demonstratie. Avem

F F F .

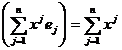
Schimbam ordinea de sumare si scotand factor comun pe

F

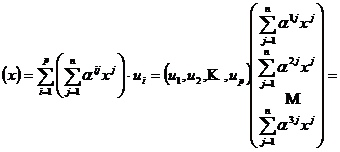
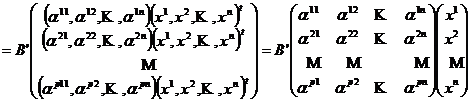
unde am scos factor comun, la dreapta, matricea =[ ]_B .

Avem deci

F ( ) = B' M(F ;B,B')[ ]_B .

Vectorul F ( ) din E' se mai scrie sub forma

F ( ) = B' F ( )]_B' .

Din tranzivitatea relatiei de egalitate aplicata pentru (11) si (12) si din faptul ca ind_E'B', obtinem

M(F ;B,B')[ ]_B = [F ( )]_B' .

Observatia Forma (11) este reprezentarea analitica a unei transformari liniare.

TEOREMA 8. Aplicatia M( ;B,B'): L (E,E') M(p,n,K) prin care oricarei relatii liniare i se asociaza o matrice in raport cu perechea de baze (B,B'), are urmatoarele proprietati:

(P.1.) M(F G; B, B ) = M(F ; B,B ) + M(G ; B,B ), F G I L (E, E

(P.2.) M(lF ; B, B lM(F ; B,B ), l I K, F I L (E, E

Demonstratie. (P.1.) Fie F G I L (E, E ) cu matricele asociate M (F ; B, B ) si M (G ; B, B ) date.

Din relatiile (9) si (10) rezulta ca F (B) = B M(F ; B,B ), G (B) = B M(G ; B,B ).

Daca notam H F G , avem

H (B) = F (B) + G (B) B M(H ; B,B ) = B (M(F ; B,B ) + M(G ; B,B

adica, revenind la notatia pentru H si tinand seama de ind_E B

M(F G ; B, B ) = M(F ; B,B ) + M(G ; B,B ).

(P.2.) Pentru transformarea liniara l F avem

(lF )(B) = l F (B) B M(lF ; B,B ) = B l M(F ; B,B

adica (tinand seama de ind_E B )

M(lF ; B, B lM(F ; B,B ) .

TEOREMA 9. Daca F I L (E, E G I L (E, E ) si B, B , B baze, respectiv, in E, E , E , atunci exista relatia

M(G F ; B,B ) = M(G ; B , B M(F ; B,B

Demonstratie. Din consideratiile de mai sus, avem

F (B) = B M (F ; B,B ), G (B ) = B M (G ; B ,B

(13) (G F )(B) = G (F (B)) = G (B M(F ; B,B )) B M(G ; B ,B M(F ; B,B

unde am folosit exprimarea (11) pentru G ( ) = G (B [ ]_B ) = B M(G ; B ,B [ ]_B cu [ ]_B = M(F ; B,B ). Cum (G F )(B) = B M(G F ; B,B ) din (13) rezulta (tinand seama de ind_E B

M(G F ; B,B ) = M(G ; B ,B M(F ;B,B

TEOREMA 10 Fie endomorfismele F F I L (E, E); B, B - baze in E si M(B, B ) matricea de trecere de la B la B . Matricele M (F ; B ) si M (F ; B) sunt asociate aceluiasi endomorfism daca si numai daca are loc relatia

M (F ; B ) = M ^-1(B, B M(F ; B) M(B, B

Demonstratie. Fie F F . In B = B M (B, B ) aplicand transformarea F obtinem F (B F (B) M(B, B ) B M (F ; B ) =B M (F ; B M(B, B ), in care, punand B = B M ^-1(B, B ), obtinem

B M (F ; B ) =B M ^-1(B, B M(F ; B) M(B, B

si ind_EB da

M (F ; B ) = M ^-1(B, B M(F ; B) M(B, B

Reciproc, presupunand adevarata relatia (14), rezulta ca pentru orice baza B din E avem

B M(F ;B )=B M ^-1(B,B M(F ; B) M(B,B

F (B )=B M(F ; B) M(B, B F (B F ( B) M(B,B )

F (B F ( B M(B,B )) F (B F (B ), B baza in E atunci

F F .

DEFINITIA 6. Doua matrice se numesc asemenea daca ele reprezinta aceeasi transformare liniara F in doua baze diferite ale spatiului vectorial.

PROPRIETATEA 4. Toate matricele asemenea unei matrice date A sunt de forma

S ^-1AS ,

unde S este o matrice nesingulara.

Demonstratie. Rezulta imediat din definitia 6 si din teorema 10.

4. Probleme rezolvate

Se considera functiile F : R³ R³ definite respectiv prin

F , cu vector fixat in R³;

F , cu R ;

F , cu R³;

F ;

F ;

F ;

F , cu R*;

F .

Rezolvare. 1) Daca , atunci F si F nu este aditiva, deci F nu este liniara.

Daca , atunci F F si pentru R avem

F F F si F este liniara (conform cu proprietatea 1.)

2) F F F , R³ si R, rezulta F I L (R³,R³).

3) Consideram si R³ si R. Avem

si

F

F F ,

deci F nu este liniara.

4) F F

F F , R³, deci F este transformare liniara.

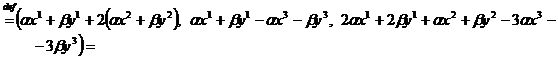
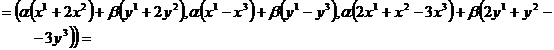
5) F este liniara ( analog cu 4 ).

6) F

F F , pentru R³.

Deci F nu este aditiva F L (R³, R³).

7) Deoarece F , rezulta ca F L (R³, R³).

8) F este liniara ( analog cu 4 ).

Fie F I L (R⁴, R⁴) data prin F . Sa se scrie Im(F ) si Ker(F

Rezolvare. Im(F ) R⁴ R⁴ a.i. F , deci

Im(F ) R⁴ .

Din definitie Ker(F ) R⁴ F , deci ,

de unde rezulta Avem

Ker(F ) R .

3. Sa se determine defectul si rangul transformarii liniare F : R³ R³ definita prin

F , cu R³,

explicitand cate o baza in Ker(F ) si in Im(F

Rezolvare. Din definitie Ker(F ) R³ F , deci Ker(F ) este multimea vectorilor pentru care

.

Obtinem sistemul care este simplu nedeterminat si are solutia cu R, deci Ker(F ) R .

Prin urmare, orice vector din Ker(F ) are forma .Vectorul este un vector liniar independent, de aceea multimea este o baza in subspatiul Ker(F ) si deci n = dim(Ker(F

Avand in vedere definitia subspatiului Im(F ) si definitia lui F , conchidem ca orice vector din Im(F ) este de forma

, cu R.

Se observa ca pentru , rezulta . Deci multimea de vectori este liniar dependenta. Mai mult, orice vector din Im(F ) se poate exprima in functie de vectorii si , care sunt liniar independenti. Rezulta ca o baza in Im(F ) este formata din acesti vectori si atunci r=dim(Im(F

Fie V₃ si spatiul vectorial real si aplicatia F : V₃ V₃ definita prin

F , cu .

i) Sa se arate ca transformarea F este liniara.

ii) Sa se scrie matricea M(F ; B) a transformarii F in aceeasi baza B in care au fost date componentele vectorilor si F .

Rezolvare. i) Se verifica usor ca, pentru orice si din V₃ si pentru orice l din R, avem F F F si F F .

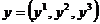
ii) Consideram baza B formata din vectorii si . Scriind vectorii si F in baza B, relatia de definitie a functiei F devine

F

sau

F F F .

Din acesta rezulta

F , F , F .

Matricea transformarii F in baza B este

M(F ; B) .

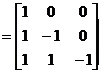
Aceasta matrice are pe coloane componentele vectorilor F , F , F ( componentele transformatelor prin F ai vectorilor bazei ) raportati la aceeasi baza B.

Un endomorfism A al spatiului vectorial cu n dimensiuni, transforma vectorii liniar independenti in vectorii corespuzatori . Sa se arate ca matricea M(A ; B) a acestei transformari A intr-o anumita baza B poate fi determinata cu ajutorul relatiei

M(A ; B) ,

unde coloanele matricelor X si Y sunt alcatuite din componentele ( coordonatele ) vectorilor , respectiv, , in aceeasi baza B.

Rezolvare. Presupunem problema rezolvata si fie

M(A ; B)

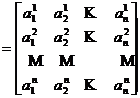
matricea cautata a transformarii A raportata la baza B . Conform definitiei avem

A ,

Scriem ca in baza B transformarea A trece vectorul in vectorul si, tinand seama de relatia (1), avem

A A A

Din aceasta rezulta

,

Aranjand componentele vectorilor pe coloane si folosind relatiile (2), obtinem ecuatia matriceala

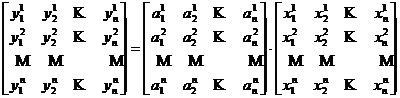
sau

M(A ; B) ,

de unde

M(A ; B) .

5 Probleme propuse

Fie R_n spatiul vectorial real al polinoamelor de grad cel mult n. Sa se arate ca functia F : R_n R_n definita prin F , R, este o transformare liniara.

Sa se cerceteze care dintre functiile definite mai jos sunt transformari liniare.

1) F , R_n , R.

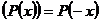
2) F , R_n , R.

3) F , R_n , R.

4) F , R_n , R.

5) F , .

6) F , .

7) F , .

8) F , .

9) F , .

3. (Derivata). Fie spatiile vectoriale reale R si R . Sa se arate ca functia D , data prin D , este o transformare liniara.

4. (Integrala definita). Fie spatiul vectorial real R f este integrabila in sens Riemann . Sa se arate ca functia I R, definita prin I , este transformare liniara.

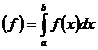
5. (Integrala nedefinita sau primitiva). Fie spatiul vectorial real

R f este functie continua .

Sa se arate ca functia

P , P , , pentru ,

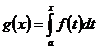
este liniara.

Fie spatiul vectorial real R f este functie continua . Sa se verifice ca aplicatia F , F pentru , este o transformare liniara.

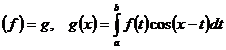
Sa se cerceteze care dintre functiile F : R³ R³ definite mai jos, sunt transformari liniare si in caz afirmativ sa se determine defectul si rangul fiecarei transformari.

F , cu R³.

F , cu R³.

F , cu R³.

F , cu R³.

F , cu R³.

Pentru problemele 3. si 5. sa se determine Ker(D) si, respectiv, Ker(P ).

Pe spatiul vectorial real P_n al functiilor polinomiale reale de grad cel mult n, se definesc functiile

P F ,

P F , R.

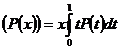
1) Sa se arate ca F si F sunt transformari liniare.

2) Sa se determine Ker(F ) si Im(F

Pentru transformarea liniara D , definita de problema 3, sa i se gaseasca matricea M( D ; B) in cazurile :

1) ,

2) , cu R fixat.

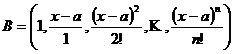
Fie F : R³ R² o transformare liniara data prin imaginile F F F unde

i) Sa se determine imaginea unui vector oarecare din R³ .

ii) Sa se determine imaginile vectorilor , si prin F

Fie o baza a spatiului vectorial V₃. Transformarea liniara U I L (V₃, V₃) duce vectorul in , in , in . Care este matricea M(U ; B) in cazurile :

1) ;

2) .

Fie F F I L (R₃ , R₃ ) doua endomorfisme definite prin relatiile :

F , F ,

F , F , F .

Sa se determine matricele transformarilor F F si, respectiv, F F , in raport cu baza canonica a spatiului R₃ .

Endomorfismul F I L (V₄, V₄) are in baza matricea

M(F ; B) .

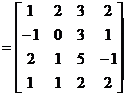
Care va fi matricea endomorfismului F , daca luam ca noua baza

1) ;

2) .

Daca A A I L (R³, R³) sunt date prin matricele

M(A ; B) , M(A ; B) ,

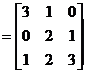
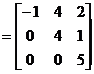
cu B baza canonica a spatiului R³, atunci

sa se determine imaginea vectorului prin transformarile A , A , A , A ;

sa se determine imaginea vectorului prin (A A ) si (A A ) ;

3) sa se determine imaginea vectorului prin A A A A A A ) si (A A ) .