Limite remarcabile. Aplicatii
1 Propozitiile 1 si 2 de mai sus sunt de fapt limite remarcabile. Le ilustram cu exercitiile care urmeaza.
E1. ![]() .
.
E ![]() .
.
E3. 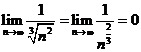 ;
;![]() .
.
E4. ![]() ;
; ![]()
2 Fie ![]() si numerele reale
si numerele reale
![]() ,
, ![]() . Atunci are loc egalitatea:
. Atunci are loc egalitatea: 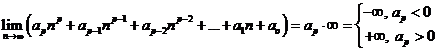
Intr-adevar: ![]()
Formula de mai sus se poate utiliza ca atare sau se poate utiliza rationamentul folosit.
E1. Calculati urmatoarele limite :
a) ![]() ; b)
; b) ![]() .
.
Solutii a) ![]() . b)
. b) ![]() =
= ![]() .
.
Fie ![]() si numerele reale
si numerele reale
![]() ,
, ![]() . Atunci avem:
. Atunci avem: 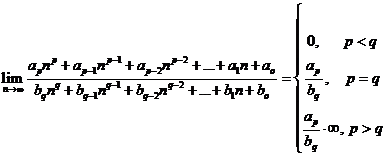 .
.
Justificarea acestei afirmatii urmeaza metoda expusa la 2 dar este util sa fie
aplicata direct (in special cazul ![]() ). Limita de mai sus elimina cazul
). Limita de mai sus elimina cazul ![]() in anumite
situatii.
in anumite
situatii.
E1. Calculati urmatoarele limite: a)
![]() ; b)
; b) ![]() .
.
Solutii Suntem in primul caz de la 3 deci ambele limite sunt egale cu 0(gradul numaratorului este mai mic decat gradul numitorului). Detaliem calculele cu titlu de exemplu. Astfel :
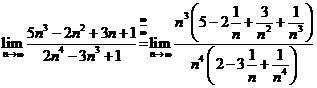
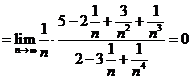 si analog
si analog 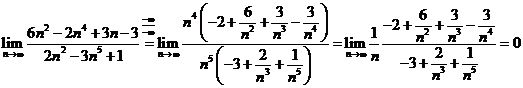 .
.
E Calculati urmatoarele limite: a) ![]() ; b)
; b) ![]() ;
;
c) 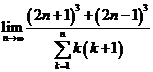 ; d)
; d) ![]() ; e)
; e) 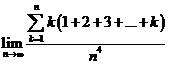 .
.
Solutii a)
Suntem in cazul al doilea de la 3
deci ![]() (gradele sunt egale si limita este egala cu
raportul coeficientilor termenilor cu gradul cel mai mare). De altfel avem
(gradele sunt egale si limita este egala cu
raportul coeficientilor termenilor cu gradul cel mai mare). De altfel avem
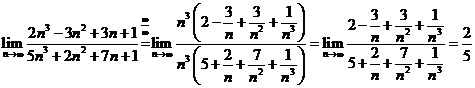 .
.
b) Avem: ![]() , deci
, deci ![]() .c) Avem:
.c) Avem: ![]() si apoi
si apoi ![]() Atunci:
Atunci: 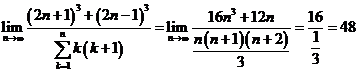 . d)
. d) ![]()
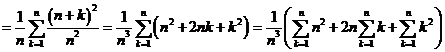 =
=
=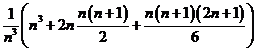 =
= ![]() . Intrucat
. Intrucat ![]() ,
, ![]() deducem ca
deducem ca ![]() . e) Avem :
. e) Avem : ![]()
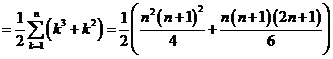 =
= ![]() . Atunci:
. Atunci: 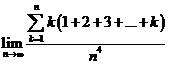
![]() +
+ ![]()
![]() .
.
E3. Calculati
urmatoarele limite: a) ![]() ; b)
; b) 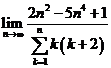 ;
;
c) 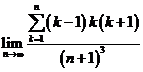 ; d)
; d) ![]() ; e)
; e) 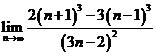 .
.
Solutii Suntem in cazul al treilea de
la 3 deci limitele sunt infinite. a)
Aplicand regula amintita avem: ![]() .Intr-adevar daca efectuam calculele avem
.Intr-adevar daca efectuam calculele avem 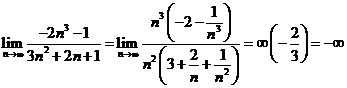 .b)
.b) ![]()
![]()
![]()
![]()
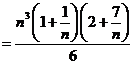 . Atunci:
. Atunci:
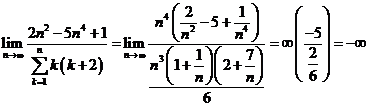 . c)
. c) ![]() =
= 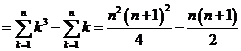
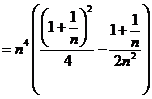 . Atunci
avem:
. Atunci
avem:
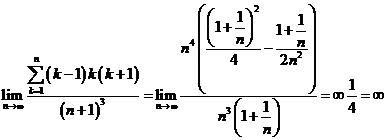 . d)
. d)![]()
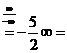
![]() ; e)
; e) ![]()
![]() . Prin urmare
. Prin urmare 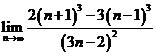
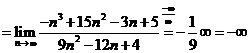 .
.
Fie ![]() arbitrar alese. Avand
in vedere Propozitia 2 deducem ca avem :
arbitrar alese. Avand
in vedere Propozitia 2 deducem ca avem : 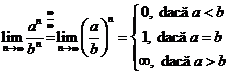 . Intrucat
. Intrucat ![]() nu este necesar
sa studiem cazul
nu este necesar
sa studiem cazul ![]() . Aceste observatii permit eliminarea cazului
. Aceste observatii permit eliminarea cazului ![]() in anumite
situatii.
in anumite
situatii.
E1. Calculati
urmatoarele limite: a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() ; e)
; e) ![]() ; f)
; f) ![]() .
.
Solutii a)  ; b)
; b) 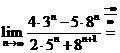
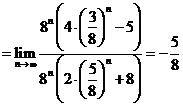 ; c)
; c) 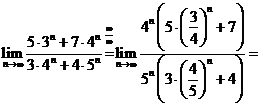
![]()
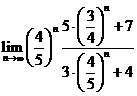
![]() 0
0![]()
![]() ; d)
; d) 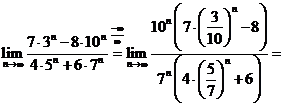
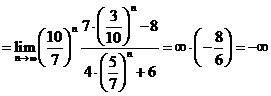 ; e) Notam
; e) Notam ![]() si pentru
calculul limitei suntem in cazul de exceptie
si pentru
calculul limitei suntem in cazul de exceptie ![]() . Analizam trei cazuri:
. Analizam trei cazuri: ![]() .
.
I) Daca ![]() atunci avem:
atunci avem:
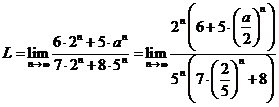 =
=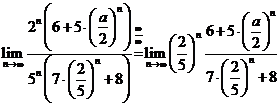 =0
=0
II) Daca ![]() atunci avem:
atunci avem: 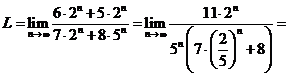
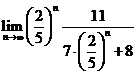
![]() .
.
III) Daca ![]() atunci analizam cazurile:
atunci analizam cazurile: ![]() .
.
i) Daca ![]() atunci avem:
atunci avem:
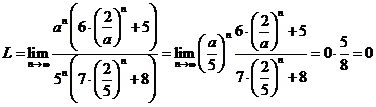 .
.
ii) Daca ![]() atunci avem:
atunci avem: 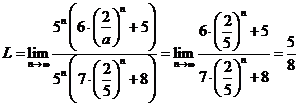 .
.
iii) Daca ![]() atunci avem:
atunci avem:
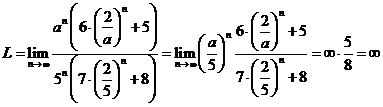 .
.
In
concluzie: 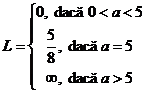 .
.
f) Notam ![]() si analizam cazurile:
si analizam cazurile: ![]() .
.
I) Pentru ![]() avem :
avem : 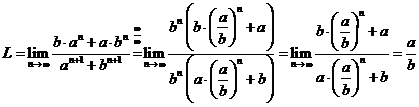 .
.
II) Pentru ![]() avem:
avem: 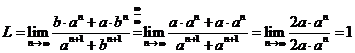 .
.
III) Pentru ![]() avem:
avem: 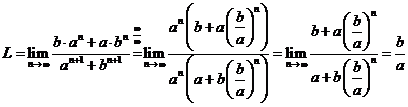 .
.
In
concluzie: 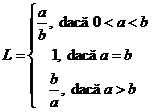 .
.
Rationamente de tipul celor utilizate la 3 pot fi utilizate pentru a elimina un caz de tipul
![]() si in anumite situatii in care apar functii
irationale.
si in anumite situatii in care apar functii
irationale.
E1. Calculati: a) ![]() ; b)
; b) 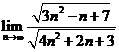 ; c)
; c) ![]() .
.
Solutii a) 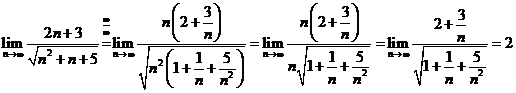 ;
;
b) 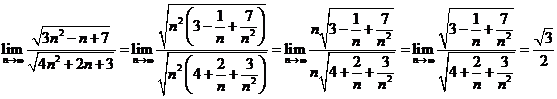 .
.
c) 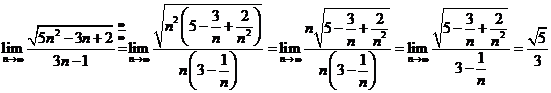 .
.
La 2 am aratat cum se elimina cazul ![]() intr-o
situatie simpla. Ilustram cum se poate elimina acest caz in alte
situatii precizand ca uneori revine la a elimina cazul
intr-o
situatie simpla. Ilustram cum se poate elimina acest caz in alte
situatii precizand ca uneori revine la a elimina cazul ![]() .
.
E1. Calculati urmatoarele limite :
a) 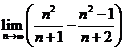 ; b)
; b) 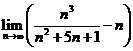 ; c)
; c) ![]() .
.
Solutii a) 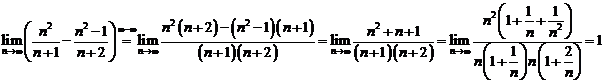
b) 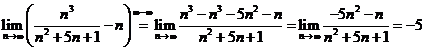
c) Utilizand formula ![]() , avem:
, avem: 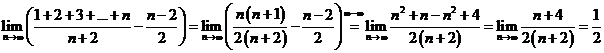
E Calculati : a) ![]() ; b)
; b) ![]() ; c)
; c) ![]()
Solutii a) 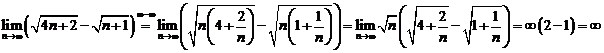
b) 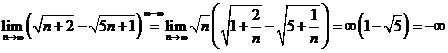
c) Daca incercam ca la a) si b)
avem 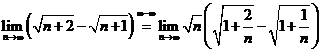 care conduce la cazul
de exceptie
care conduce la cazul
de exceptie ![]() . In aceasta situatie inmultim si
impartim cu conjugata :
. In aceasta situatie inmultim si
impartim cu conjugata : ![]()
E3. Calculati urmatoarele limite: a)
![]() ; b)
; b) ![]()
c)![]() ;d)
;d)![]() ;e)
;e) ![]() .
.
Solutii a) 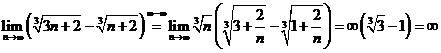
b) 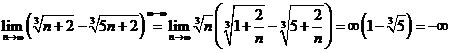 ; c) Rationamentul de mai sus conduce la
; c) Rationamentul de mai sus conduce la 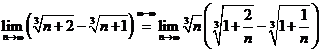 , deci la cazul de exceptie
, deci la cazul de exceptie ![]() . Procedam ca mai sus:
. Procedam ca mai sus: 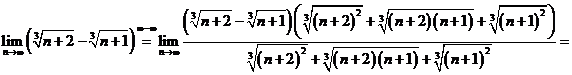
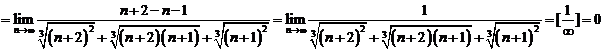
d) 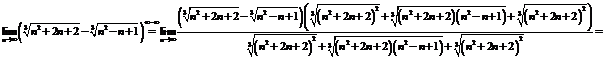
![]()
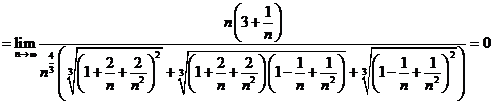
e) 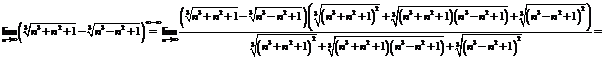
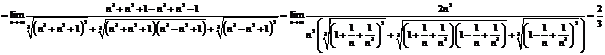
E4. Calculati urmatoarele limite :
a)![]() ; b)
; b)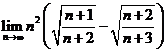
Solutii a) ![]()
![]()
b) 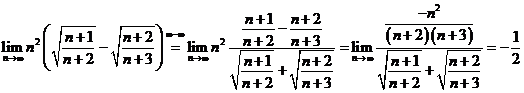
E5. Calculati limitele sirurilor ![]() date prin formula
termenului general:
date prin formula
termenului general:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]() (am notat cu
(am notat cu ![]() partea
fractionara a numarului real
partea
fractionara a numarului real ![]() ).
).
Solutii a)
Pentru orice numar real ![]() avem
avem ![]() , deci
, deci![]() . Pe de alta parte avem:
. Pe de alta parte avem: ![]() din care deducem
inegalitatile :
din care deducem
inegalitatile : ![]() deci
deci ![]() din care deducem
din care deducem ![]() . Pentru calculul limitei suntem in cazul
. Pentru calculul limitei suntem in cazul ![]() care este caz de exceptie deci trebuie eliminat. Avem:
care este caz de exceptie deci trebuie eliminat. Avem: 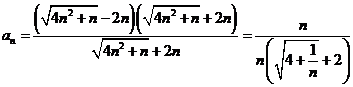 si deci
si deci ![]() .
.
b) Avem: ![]() din care deducem
inegalitatile
din care deducem
inegalitatile ![]() deci
deci ![]() si prin urmare
obtinem:
si prin urmare
obtinem: ![]()
![]()
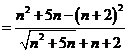
![]() , deci
, deci
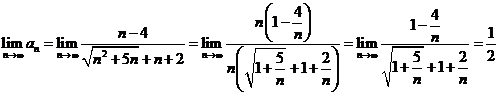
c) Din ![]() deducem
deducem ![]() . Dar
. Dar 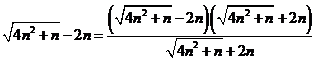
![]()
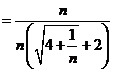 . Avem :
. Avem : 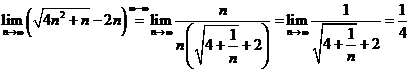 , deci
, deci ![]() .
.
d) Avem ![]() si prin urmare
si prin urmare ![]() . Deci
. Deci ![]() , pentru orice
, pentru orice ![]() . Atunci
. Atunci ![]() . Deoarece
. Deoarece 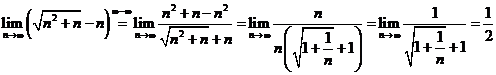 deducem ca
deducem ca ![]() .
.
E6. Determinati constantele reale a,b astfel incat sa aiba loc egalitatile:
a) 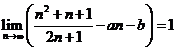 ; b)
; b) ![]() ;
;
c) ![]() .
.
Solutii a)
Fie 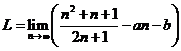 . Atunci
. Atunci 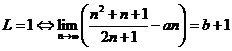 . Dar
. Dar 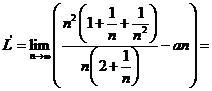
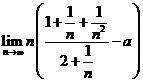
![]() . Daca
. Daca ![]() , atunci
, atunci ![]() , imposibil. Deci
, imposibil. Deci ![]() si
si 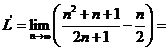
![]() . Dar
. Dar ![]() , deci se impune
, deci se impune ![]() adica
adica ![]() .
.
b) Fie![]() . Atunci
. Atunci ![]() .
.
Notam ![]() si avem
si avem![]()
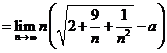 . Daca
. Daca ![]() atunci
atunci ![]() ,ceea ce nu convine. Deci
,ceea ce nu convine. Deci ![]() si
si 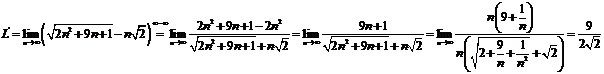 Dar
Dar ![]() deci avem:
deci avem: ![]() .
.
c) 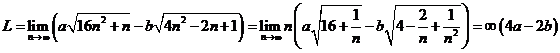 .
.
Daca ![]() , atunci
, atunci ![]() . Deci se impune
. Deci se impune ![]() adica
adica ![]() si avem
si avem ![]()
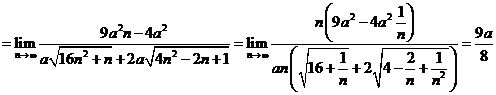 . Deci se impune
. Deci se impune ![]() din care avem
din care avem ![]() si prin urmare
si prin urmare ![]() .
.
Fie ![]() sunt doua
siruri astfel incat
sunt doua
siruri astfel incat ![]() . Avand in vedere ca
. Avand in vedere ca ![]() si ca
si ca ![]() deducem ca,
uneori, cazul
deducem ca,
uneori, cazul ![]() se poate reduce la cazul
se poate reduce la cazul ![]() . De asemenea daca
. De asemenea daca ![]() atunci din
atunci din 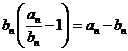 deducem ca,
uneori, cazul
deducem ca,
uneori, cazul ![]() se reduce la cazul
se reduce la cazul ![]() . Exercitiile E3, E4 si E5 de la 6 pun in evidenta astfel de
situatii. In continuare dam alte exemple pentru eliminarea cazului
. Exercitiile E3, E4 si E5 de la 6 pun in evidenta astfel de
situatii. In continuare dam alte exemple pentru eliminarea cazului ![]() . Vom utiliza propozitia de mai jos(numita adeseori
"lema clestelui").
. Vom utiliza propozitia de mai jos(numita adeseori
"lema clestelui").
Propozitia
3 Daca ![]() sunt trei siruri
astfel incat
sunt trei siruri
astfel incat ![]() sunt convergente cu
sunt convergente cu ![]() si
si ![]() , atunci si
, atunci si ![]() este convergent
si
este convergent
si ![]() .
.
E1. Calculati limitele sirurilor date prin formula termenului general:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]()
Solutii a) Avem ![]() , deci pentru calculul limitei suntem in cazul
, deci pentru calculul limitei suntem in cazul ![]() . Avem:
. Avem: 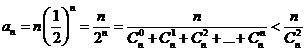 . Dar
. Dar 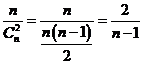 ,
,![]() . Deducem
. Deducem ![]() si pentru ca
si pentru ca
![]() obtinem ca
obtinem ca ![]() .
.
b) Ca si la a) avem ![]() , deci pentru calculul limitei sirului suntem in cazul
, deci pentru calculul limitei sirului suntem in cazul ![]() . Evident
. Evident 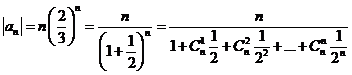
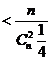 . Dar
. Dar 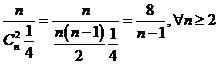 deci
deci ![]() si pentru ca
si pentru ca
![]() deducem ca
deducem ca ![]() . Prin urmare avem
. Prin urmare avem ![]() .c) Avem
.c) Avem ![]() , deci pentru calculul limitei sirului suntem in cazul
, deci pentru calculul limitei sirului suntem in cazul ![]() . Dar:
. Dar: 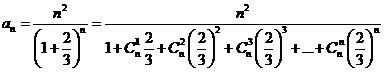
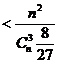 . Pe de alta parte:
. Pe de alta parte: 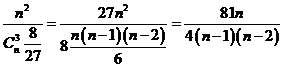 , deci
, deci ![]() si pentru ca
si pentru ca
![]() obtinem
obtinem ![]() .
.
E Calculati limitele sirurilor date prin formula termenului general:
a) ![]() ; b)
; b) ![]() ;
;
c) ![]() ;d)
;d) ![]() .
.
e) ![]() ; f)
; f) ![]() .
.
Solutii Sa observam ca termenul general al acestor siruri
este o suma de n termeni dintre
care fiecare are limita egala cu 0. Prin urmare pentru calculul limitei
oricaruia dintre ei suntem in cazul de exceptie ![]() .
.
a) Evident avem
inegalitatile ![]() . Scriind aceste inegalitati pentru
. Scriind aceste inegalitati pentru ![]() obtinem:
obtinem: ![]()
![]() . Adunand membru cu membru aceste inegalitati,
obtinem:
. Adunand membru cu membru aceste inegalitati,
obtinem: ![]() . Intrucat
. Intrucat ![]() ,deducem
,deducem
![]() . b) Din inegalitatile
. b) Din inegalitatile ![]() deducem :
deducem :
![]() . Adunand membru cu membru aceste inegalitati,
obtinem:
. Adunand membru cu membru aceste inegalitati,
obtinem: 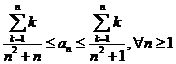 . Deoarece
. Deoarece ![]() obtinem:
obtinem:
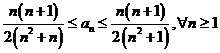 . Dar
. Dar 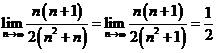 , deci
, deci ![]() .
.
c) Din inegalitatile ![]() , prin adunare membru cu membru, deducem:
, prin adunare membru cu membru, deducem: ![]() , adica
, adica ![]() . Deoarece
. Deoarece 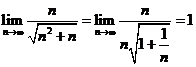 si
si 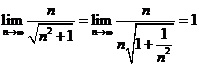 ,avem
,avem ![]() .
.
d) Din inegalitatile ![]() , prin inmultire cu k,
avem
, prin inmultire cu k,
avem ![]() si deci
si deci 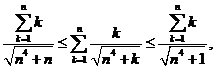 adica
adica
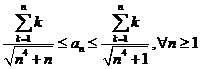 . Dar
. Dar ![]() si atunci
obtinem:
si atunci
obtinem:
![]() . Deoarece
. Deoarece 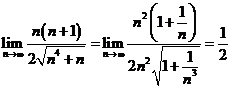 si
si 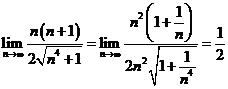 , avem
, avem ![]() . e) Avem
. e) Avem ![]() , deci:
, deci:
![]()
Dar ![]() , deci
, deci ![]() . f)
. f) ![]() ,
,
deci 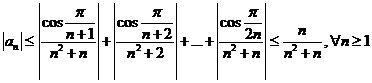 si din
si din ![]() deducem
deducem
![]() .
.
E3. Fie ![]() arbitrar.
Calculati limita sirului dat prin formula termenului general:
arbitrar.
Calculati limita sirului dat prin formula termenului general:
![]()
Solutii Din inegalitatile ![]() , valabile pentru orice
, valabile pentru orice ![]() , avem
, avem ![]() . Dar
. Dar ![]() , deci avem
, deci avem ![]() . Insumand dupa k
aceste inegalitati se obtine
. Insumand dupa k
aceste inegalitati se obtine ![]() . Inmultind cu
. Inmultind cu ![]() obtinem
obtinem 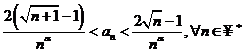 . Avem
. Avem 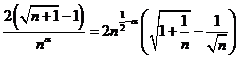 si
si 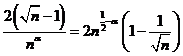 . Atunci
. Atunci 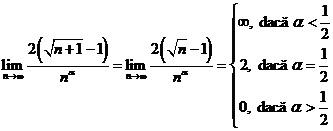 .
.
Deducem ca 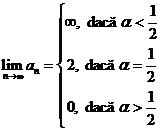 .
.
In exercitiul urmator vom utiliza afirmatiile din propozitiile care urmeaza.
Propozitia 4 Daca ![]() este un sir
convergent cu
este un sir
convergent cu![]() , atunci :
, atunci : ![]() si
si
![]() .
.
Propozitia 5 Daca ![]() , atunci
, atunci ![]() .
.
E4. Calculati limitele sirurilor ![]() date prin formula
termenului general:
date prin formula
termenului general:
a) ![]() ; b)
; b)![]() ;c)
;c) ![]() ;d)
;d) ![]() .
.
Solutii
Deoarece ![]() pentru calculul
limitelor suntem in cazul
pentru calculul
limitelor suntem in cazul ![]() , pe care il aducem la cazul eliminat de Propozitia 4.
, pe care il aducem la cazul eliminat de Propozitia 4.
a) 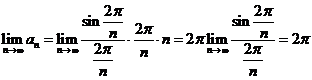 ; b)
; b) 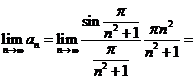
![]() ;
;
c) 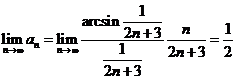 ; d)
; d) ![]()
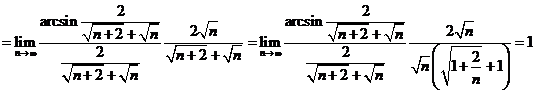
In principiu pentru a elimina cazul de exceptie ![]() se utilizeaza
teorema de mai jos.
se utilizeaza
teorema de mai jos.
Teorema Sirul ![]() dat prin
dat prin ![]() este convergent
si limita sa este un numar
situat in intervalul
este convergent
si limita sa este un numar
situat in intervalul ![]() .
.
Observatie Se
noteaza ![]() .
.
Corolar Fie ![]() doua siruri
astfel incat
doua siruri
astfel incat ![]() . Atunci:
. Atunci:
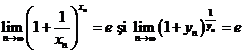 .
.
E1. Calculati limitele sirurilor ![]() date prin formula
termenului general:
date prin formula
termenului general:
a) 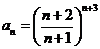 ; b)
; b) ![]() ; c)
; c) 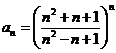 ; d)
; d) 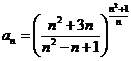 .
.
Solutii a) 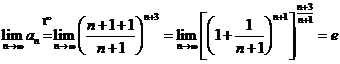 deoarece
deoarece ![]() .
.
b) 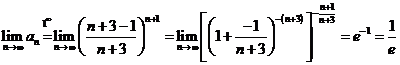 deoarece
deoarece ![]() .
.
c) 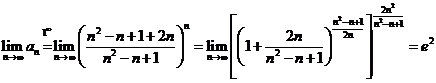 .
.
d) 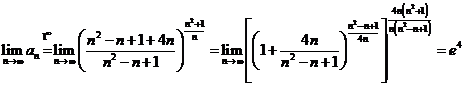 .
.
E Calculati limitele sirurilor ![]() date prin formula termenului general:
date prin formula termenului general:
a) 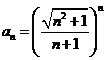 ; b)
; b) 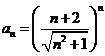 ; c)
; c) 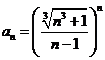 ; d)
; d) 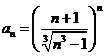 .
.
Solutii a) Avem:
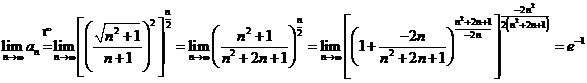 .
.
b) 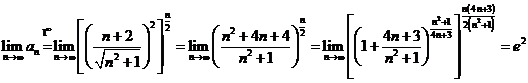 .
.
c) Avem: 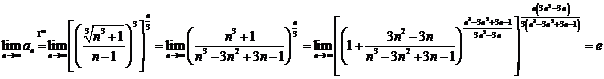
d) Avem: 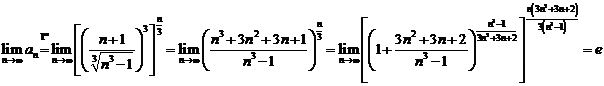
E3. Calculati limitele sirurilor ![]() date prin formula termenului general:
date prin formula termenului general:
a) 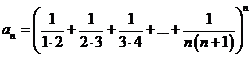 ; b)
; b) 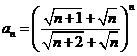 ;
;
c) 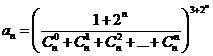 ; d)
; d) 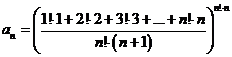 .
.
Solutii a) Calculam suma:
![]() .
.
Deci
avem : 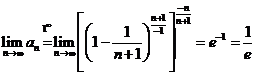 .
.
b) 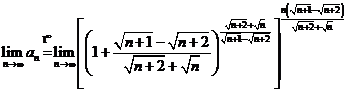 . Deoarece:
. Deoarece: ![]()
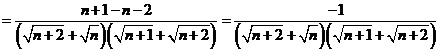 avem :
avem :
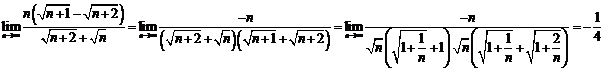 si prin urmare
si prin urmare ![]() .
.
c) 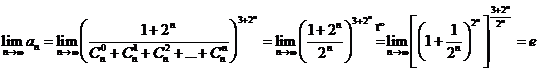 .
.
d) Calculam suma:
![]()
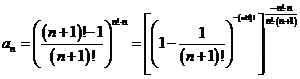 si
si 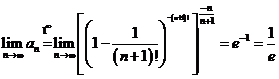 .
.
Exercitiul de mai jos este important pentru eliminarea cazului ![]() .
.
E1. Aratati ca ![]() .
.
Solutie
Pentru ![]() notam
notam![]() . Evident
. Evident ![]() . Atunci:
. Atunci: ![]() si deci
si deci ![]() , adica
, adica ![]() din care deducem
din care deducem ![]() . Asadar
. Asadar ![]() si pentru ca
si pentru ca
![]() , avem
, avem ![]() . Dar
. Dar ![]() si obtinem
si obtinem ![]() din care deducem
din care deducem ![]() .
.
Observatie
Avem evident ![]() si
si ![]() ceea ce justifica afirmatia ca E1 este un mod
de a elimina cazul
ceea ce justifica afirmatia ca E1 este un mod
de a elimina cazul ![]() .
.
E Calculati ![]() .
.
Solutie Cum ![]() , deci pentru calculul limitei suntem in cazul
, deci pentru calculul limitei suntem in cazul ![]() .
.
Avem ![]() si pentru ca
si pentru ca
![]() deducem
deducem ![]() .
.
E3. Calculati ![]() unde
unde ![]() este fixat.
este fixat.
Solutie Evident este o generalizare a exercitiului precedent si procedam analog.
![]() . Deoarece :
. Deoarece : 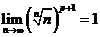 , deducem
, deducem ![]() .
.
Alte
exemple de eliminare a cazului ![]() sunt date de
exercitiul urmator.
sunt date de
exercitiul urmator.
E4. Sa se calculeze: a)![]() ;b)
;b)![]() ;c)
;c)![]() ;
;
d) ![]() ; e)
; e) ![]() .
.
Solutii a) ![]() si, deoarece
si, deoarece ![]() , deducem
, deducem
![]() ; b) Fie
; b) Fie ![]() . Atunci
. Atunci ![]() . Deducem ca:
. Deducem ca:
![]() si, cum
si, cum ![]() , deducem
, deducem ![]() .
.
c) Fie ![]() . Atunci:
. Atunci: ![]()
![]() . Dar
. Dar
![]() , deci
, deci ![]() ;
;
d) ![]() . Din
. Din ![]() deducem
deducem ![]() .
.
e) Notam ![]() . Atunci
. Atunci ![]() , din care deducem
, din care deducem ![]() . Intrucat
. Intrucat ![]() , deducem ca
, deducem ca ![]() .
.
Cazul ![]() apare mai rar in
calculul limitelor de siruri intrucat daca
apare mai rar in
calculul limitelor de siruri intrucat daca ![]()
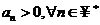 , atunci
, atunci 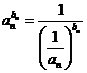 . Pentru ca:
. Pentru ca: ![]() deducem ca
trebuie sa eliminam un caz de forma
deducem ca
trebuie sa eliminam un caz de forma ![]() . De asemenea
. De asemenea ![]() , ceea ce arata ca acest caz se poate reduce la
cazul
, ceea ce arata ca acest caz se poate reduce la
cazul ![]() .
.
E1. Calculati: a) 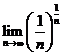 ; b)
; b) 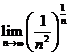 ; c)
; c) 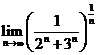 ; d)
; d) 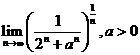 .
.
Solutie Vom folosi rezultatele obtinute la E1 si E4 din 9.
a) 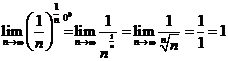 ; b)
; b) 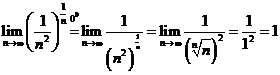 ;
;
c) 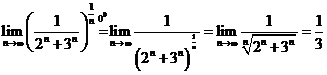 ; d)
; d) 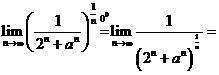
![]() ( vezi 9,
exercitiul E4.b).
( vezi 9,
exercitiul E4.b).
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |