
Reducerea formei patratice la expresia canonica
TEOREMA 1.6.5.(Metoda lui Gauss). O forma patratica P : E R se poate scrie totdeauna sub forma canonica printr-o schimbare convenabila a bazei spatiului.
Demonstratie. Fie o forma patratica
P 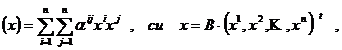
in care ![]() este baza
a spatiului
E. Punem in evidenta
toti
termenii care il
contin
pe
este baza
a spatiului
E. Punem in evidenta
toti
termenii care il
contin
pe ![]() si
anume
si
anume ![]() in
care formam
patratul
perfect (
in
care formam
patratul
perfect (![]() ) obtinand
) obtinand
![]()
si din care trebuie sa scadem pe
![]()
Deci P x) se scrie
P ![]() P
P ![]() ,
,
unde P (![]() ) este o forma patratica
care nu-l contine
pe
) este o forma patratica
care nu-l contine
pe ![]() .
.
Procedeul
se continua
si
pentru P .
Dupa
![]() astfel de operatii
obtinem
astfel de operatii
obtinem
P ![]() ,
,
unde :
![]()
B noua baza(care, eventual, se determina usor folosind schimbarile de coordonate)
![]()
![]()
ceilalti coeficienti
![]() si
coordonate
si
coordonate ![]() , i = 2, ,n, se
determina
din aproape in
aproape.
, i = 2, ,n, se
determina
din aproape in
aproape.
Observatia 1. Procedeul
folosit nu este unic; aici am inceput cu ![]() , dar putem incepe cu oricare
, dar putem incepe cu oricare ![]() si
sa
le separam.
si
sa
le separam.
Observatia 1. Daca ![]() ,
, ![]() si
P nu este identic nula, atunci
exista
cel putin
un element
si
P nu este identic nula, atunci
exista
cel putin
un element ![]() , pentru
, pentru ![]() . Prin transformarea de coordonate
. Prin transformarea de coordonate
![]() , expresia formei patratice
devine
, expresia formei patratice
devine
P ![]() ,
,
in care cel putin
unul din elementele ![]() ,
, ![]() , este nenul ( deoarece
, este nenul ( deoarece ![]() ).
).
Presupunand ![]() , procedeul se continua cu expresia (10).
, procedeul se continua cu expresia (10).
TEOREMA 1.6.6. (Metoda lui Jacobi) Fie E spatiu
vectorial real, P : E
R o forma patratica,
F forma biliniara simetrica
asociata, ![]() o baza in E,
o baza in E,
M
(F ;
![]() )
)![]() ,
,
P ![]() M (F ;
B
M (F ;
B![]() B)
B)![]() .
.
Daca toti determinantii
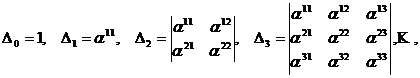
![]() M(F ;B
M(F ;B![]() B)
B)
numiti
determinanti minori
principali ai matricei M(F ;
B![]() B) sunt nenuli, atunci exista o baza
B) sunt nenuli, atunci exista o baza
![]() ,
,
obtinuta din B prin matricea de trecere triunghiulara
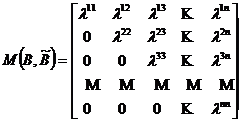 ,
,
in care P are forma canonica
P ![]() , cu
, cu ![]() .
.
Demonstratie.
In
baza ![]()
P ![]() ( F ;
( F ;![]() , cu
, cu ![]() F
F ![]()
Vom demonstra ca
se poate determina o transformare triunghiulara de forma (12)
astfel ca ![]() 0, pentru
0, pentru ![]() . Deoarece F
. Deoarece F ![]() = F
= F ![]() , este suficient ca
, este suficient ca
![]() F
F ![]() ,
, ![]() , cu
, cu ![]() ,
,
sau, folosind
transformarea (12), F 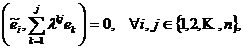 cu
cu ![]()
![]() F
F ![]()
![]() , cu
, cu ![]()
F ![]()
![]()
Adaugam, pentru simplificarea calculelor, conditiile
F ![]()
![]() .
.
Cu dezvoltarile
F ![]() F
F ![]() F
F 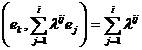 F
F ![]()
![]() ,
,
pentru ca
sunt scalari si
![]() sunt dati,
iar
sunt dati,
iar ![]() sunt necunoscuti,
relatiile
(15) si
(16) se scriu in
sistemul (17)
sunt necunoscuti,
relatiile
(15) si
(16) se scriu in
sistemul (17)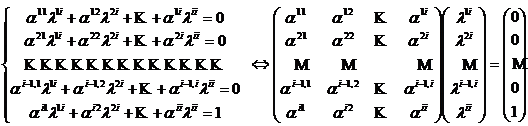 ,
,
pentru ![]() . Prin ipoteza Di
0, deci acest sistem va determina in mod unic co-
. Prin ipoteza Di
0, deci acest sistem va determina in mod unic co-
ordonatele ![]() ale vectorului
ale vectorului ![]() in baza B.
in baza B.
De exemplu, ![]() (din rezolvarea
sistemelor de ecuatii liniare si omogene).
(din rezolvarea
sistemelor de ecuatii liniare si omogene).
In
baza![]() astfel obtinuta, forma patratica
va avea forma canonica
astfel obtinuta, forma patratica
va avea forma canonica
P ![]() ,
,
cu coeficientii
![]() F
F ![]() ,
,
care trebuie determinati. Pentru aceasta facem dezvoltarea
![]() F
F ![]() F
F 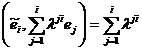 F
F ![]() ,
,
si, tinand seama de (15) si (16), rezulta
![]() .
.
Cu ![]() dedus din sistemul (17) rezulta
dedus din sistemul (17) rezulta
![]() ,
, ![]() .
.
Pentru ![]() , avem
, avem
![]() F
F ![]() F
F ![]() .
.
Pe de alta parte,
![]() F
F ![]() F
F ![]() F
F ![]()
si rezulta
![]() .
.
Deci in
baza ![]() , determinata prin procedeul
de mai sus, forma patratica are forma canonica (13) .
, determinata prin procedeul
de mai sus, forma patratica are forma canonica (13) .
Observatia 1. Teorema lui Jacobi permite sa se construiasca o baza pentru re-ducerea formei patratice la forma canonica si sa se calculeze coeficientii formei canonice. Acesti coeficienti arata numarul termenilor negativi cat si ai celor pozitivi.
TEOREMA 1. (Metoda valorilor proprii si a vectorilor proprii). Daca
P : E R este o forma patratica, atunci exista o baza B = (u1, u2, , un) a lui E fata de care expresia canonica a formei este
P ![]() ,
,
unde ![]() sunt valorile proprii ale matricei formei, fiecare valoare proprie fiind scrisa de atatea
ori cat
este multiplicitatea sa, iar
sunt valorile proprii ale matricei formei, fiecare valoare proprie fiind scrisa de atatea
ori cat
este multiplicitatea sa, iar ![]() , i = 1, , n, sunt coordonatele lui
, i = 1, , n, sunt coordonatele lui ![]() in aceasta baza.
in aceasta baza.
Demonstratie.
Deoarece matricea formei P este o matrice simetrica
reala,
ea admite numai valori proprii reale si se poate
diagonaliza. Atunci baza cautata B
este formata
din vectorii proprii ortonormati ai matricei formei M(F ;![]() ). In baza B obtinem
expresia canonica
a formei P
si
anume, daca
M(B, B )
este matricea de trecere de la B la B ,
prin schimbarea [
). In baza B obtinem
expresia canonica
a formei P
si
anume, daca
M(B, B )
este matricea de trecere de la B la B ,
prin schimbarea [![]() ]
]![]() = M (B, B ) [
= M (B, B ) [![]() ]
]![]() , avem
, avem
P ![]() ( F ;
( F ;![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |