Ecuatii trigonometrice
Ecuatiile trigonometrice sunt
ecuatii in care necunoscuta figureaza in argumente ale functiilor trigonometrice. Daca necunoscuta se
afla in ecuatie si altfel decat sub semnul unei functii
trigonometrice , de exemplu ![]() , atunci aceste ecuatii se numesc mixte. In cele ce urmeaza voi prezenta cateva tipuri de
ecuatii trigonometrice simple
,alegand exemple pe care le voi rezolva, din variantele de bacalaureat de anul
acesta.Incep acest articol, prin trecerea in revista a tuturor subiectelor
legate de aceasta tema din variantele de bacalaureat M1,subiectul I.
, atunci aceste ecuatii se numesc mixte. In cele ce urmeaza voi prezenta cateva tipuri de
ecuatii trigonometrice simple
,alegand exemple pe care le voi rezolva, din variantele de bacalaureat de anul
acesta.Incep acest articol, prin trecerea in revista a tuturor subiectelor
legate de aceasta tema din variantele de bacalaureat M1,subiectul I.
Sa
se rezolve in multimea ![]() ecuatiile:
ecuatiile:
a). ![]() ; b).
; b). ![]() c).
c). ![]() d).
d). ![]() .
.
2. Sa
se rezolve in multimea ![]() ecuatiile:
ecuatiile:
a).![]() ; b).
; b). ![]() c).
c). ![]() .
.
3. Sa
se rezolve in multimea ![]() ecuatiile: a)
ecuatiile: a) ![]() ; b).
; b). ![]() ;
;
4. Sa se rezolve ecuatiile in ![]() :
:
a). ![]() ; b).
; b). ![]() ; c).
; c). ![]() ; d).
; d). 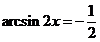 ;
;
e). ![]() ; f).
; f). ![]() ; g).
; g). ![]() ; h).
; h). ![]() ;
;
i). ![]() ; j).
; j). ![]() ; k).
; k). ![]() .
.
5. Sa
se rezolve in multimea ![]() ecuatiile: a)
ecuatiile: a) ![]() ; b).
; b). ![]() .
.
6. Sa
se rezolve in ![]() ecuatiile: a)
ecuatiile: a) ![]() ; b).
; b). ![]() .
.
7. Sa se rezolve in multimea numerelor reale ecuatia ![]() .
.
8. Sa
se rezolve in intervalul ![]() ecuatia
ecuatia ![]() .
.
9. Numerele
reale x si y verifica egalitatea ![]() . Sa se arate
ca
. Sa se arate
ca ![]() .
.
Ecuatii trigonometrice fundamentale
Ecuatiile cuprinse sub aceasta titulatura sunt :
1) ![]() ,
, ![]() . Daca
. Daca ![]() ,ecuatia nu are solutii, iar daca
,ecuatia nu are solutii, iar daca ![]() ,multimea S de
solutii a ecuatiei este :
,multimea S de
solutii a ecuatiei este :
![]() .
.
2) ![]() ,
, ![]() . Daca
. Daca ![]() ,ecuatia nu are solutii, iar daca
,ecuatia nu are solutii, iar daca ![]() ,multimea S de
solutii a ecuatiei este:
,multimea S de
solutii a ecuatiei este:
![]() .
.
3) ![]() ,
, ![]() .Solutiile acestei ecuatii sunt date de
multimea
.Solutiile acestei ecuatii sunt date de
multimea ![]() .
.
4) ![]() ,
, ![]() .Solutiile acestei ecuatii sunt date de
multimea
.Solutiile acestei ecuatii sunt date de
multimea ![]()
Daca intervin mai multe
functii trigonometrice , dar care au acelasi argument , de exemplu ![]() , atunci exprimam
ambele functii trigonometrice prin alte functii, de
exemplu :
, atunci exprimam
ambele functii trigonometrice prin alte functii, de
exemplu :
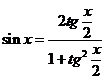
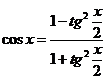
Daca intervine numai o functie trigonometrica , dar cu argumente diferite , atunci cu ajutorul formulelor trigonometrice de adunare transformam functiile astfel ca sa avem in expresie un argument unic.
Exemplul 1 Diferite functii trigonometrice ale aceluiasi argument ( vezi ex. 3,b) :
![]()
![]()
Exprimam ![]() si
si ![]() in functie de
in functie de ![]() , pentru
, pentru ![]() ,
, ![]() si se obtine
si se obtine 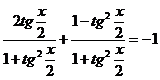
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]() .Cum
.Cum ![]() , alegem doar
, alegem doar ![]() .Prin rezolvarea
ecuatiei cu ajutorul acestor formule in care folosim
.Prin rezolvarea
ecuatiei cu ajutorul acestor formule in care folosim ![]() excludem solutia
excludem solutia ![]() caci
caci ![]() nu este definita
pentru aceste valori.Totusi
nu este definita
pentru aceste valori.Totusi ![]() este o solutie a ecuatiei respective.Deci
este o solutie a ecuatiei respective.Deci ![]() .
.
Observatie: Intrucat numarul ![]() , nu exista daca
, nu exista daca ![]() ,
, ![]() , rezulta ca eventualele
solutii de aceasta forma se pierd; prin urmare , in final,
trebuie verificate in ecuatie si numerele respective .
, rezulta ca eventualele
solutii de aceasta forma se pierd; prin urmare , in final,
trebuie verificate in ecuatie si numerele respective .
Ecuatii care contin functii de acelasi nume
1) ![]()
![]()
![]() ,
, ![]() ; 3)
; 3) ![]()
![]()
![]() ,
, ![]() .
.
2) ![]()
![]()
![]() ,
, ![]() ;
; ![]() ,
, ![]()
4).
![]()
![]()
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Exemplul 2. Aceeasi functie trigonometrica cu argumente diferite:
![]() ,
, ![]()
In rezolvarea acestei ecuatii se
foloseste formula de transformare a sumei in produs: ![]() ;ecuatia devine
;ecuatia devine ![]()
![]()
![]() sau
sau ![]() . Multimea de solutii a ecuatiei
. Multimea de solutii a ecuatiei ![]() este
este ![]() ,iar multimea de solutii a ecuatiei
,iar multimea de solutii a ecuatiei ![]() este
este ![]() . Deci multimea solutiilor ecuatiei este
. Deci multimea solutiilor ecuatiei este ![]() .
.
Exemplul 3. Diferite functii trigonometrice cu argumente diferite( vezi ex. 4, h):
![]()
![]()
Utilizand formula ![]() obtinem
obtinem ![]()
![]()
![]()
![]()
![]() sau
sau ![]() .Multimea de solutii a ecuatiei
.Multimea de solutii a ecuatiei ![]() este
este ![]() ,iar multimea de solutii a ecuatiei
,iar multimea de solutii a ecuatiei ![]() este
este ![]() .Deci multimea solutiilor ecuatiei este
.Deci multimea solutiilor ecuatiei este ![]() .
.
Ecuatiile
liniare in sinx si cosx sunt de forma ![]() , unde a, b, c
sunt numere reale,
, unde a, b, c
sunt numere reale, ![]() (alte cazuri conduc la
ecuatii usor de analizat).
(alte cazuri conduc la
ecuatii usor de analizat).
Distingem urmatoarele metode de rezolvare :
a) Metoda unghiului auxiliar . Se
imparte ecuatia prin "a" si
se obtine![]() ; se noteaza
; se noteaza ![]() , deci
, deci ![]() ,
, ![]() ; dupa cateva calcule se ajunge la ecuatia
elementara
; dupa cateva calcule se ajunge la ecuatia
elementara ![]() .
.
b) Metoda substitutiei . Cu ajutorul formulelor 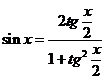
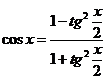 obtinem o ecuatie de gradul al
doilea cu necunoscuta
obtinem o ecuatie de gradul al
doilea cu necunoscuta ![]() .
.
Exemplul 4. ![]()
![]() (vezi ex.2 ,b).
(vezi ex.2 ,b).
Rezolv
ecuatia utilizand metoda unghiului
auxiliar ; se imparte ecuatia prin ![]() si se obtine
si se obtine ![]()
![]()
![]()
![]()
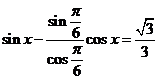
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Cum ![]() , alegem
, alegem ![]() si
si ![]() .Deci
.Deci ![]() .
.
Exemplul 5. ![]() ,
, ![]() (vezi ex. 4, j).
(vezi ex. 4, j).
Aceasta ecuatie se rezolva
usor cu ajutorul cofunctiei ![]() , observandu-se ca
, observandu-se ca ![]() .Ecuatia devine
.Ecuatia devine ![]()
![]()
![]()
![]()
![]()
![]() .
.
Multimea
solutiilor ecuatiei este ![]()
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |