
Limite de functii reale de o variabila reala
1. Definitie.
Fie ![]() o functie
reala de o variabila reala si
o functie
reala de o variabila reala si ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() . Spunem ca numarul
. Spunem ca numarul ![]() este limita
functiei
este limita
functiei ![]() in punctul
in punctul ![]() si scriem
si scriem ![]() , daca pentru orice vecinatate
, daca pentru orice vecinatate ![]() exista o
vecinatate
exista o
vecinatate ![]() a.i.
a.i. ![]() .
.
2. Observatie.
(1). Potrivit definitiei, in punctul ![]() functia
functia ![]() nu este neaparat
definita si daca este definita atunci in definitia
limitei se ia
nu este neaparat
definita si daca este definita atunci in definitia
limitei se ia ![]() .
.
(2). Daca se tine seama de
definitia vecinatatii unui punct, atunci ![]() este limita
functiei
este limita
functiei ![]() in punctul
in punctul ![]() daca si
numai daca pentru orice vecinatate
daca si
numai daca pentru orice vecinatate ![]() exista o
vecinatate
exista o
vecinatate ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() si
si ![]() sa avem
sa avem ![]() .
.
(3). Numarul ![]() este limita
functiei
este limita
functiei ![]() in punctul
in punctul ![]() daca si
numai daca oricare ar fi sirul
daca si
numai daca oricare ar fi sirul ![]() de puncte din
de puncte din ![]() , cu
, cu ![]() si
si ![]() sa avem
sa avem ![]() .
.
Limita ![]() exista si este finita
daca si numai daca
exista si este finita
daca si numai daca ![]() astfel ca,
oricare ar fi
astfel ca,
oricare ar fi ![]() ,
, ![]() si
si ![]() sa avem
sa avem ![]() .
.
Limita functiei ![]() in punctul
in punctul ![]() este
este ![]() (respectiv
(respectiv ![]() ) si scriem
) si scriem ![]() , daca si numai daca
, daca si numai daca ![]() astfel ca,
oricare ar fi
astfel ca,
oricare ar fi ![]() , cu
, cu ![]() sa avem
sa avem ![]() (respectiv
(respectiv ![]() ) sau echivalent pentru orice interval
) sau echivalent pentru orice interval ![]() exista un
interval
exista un
interval ![]() centrat in
centrat in ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() sa avem
sa avem ![]() .
.
3. Limitele
laterale finite ale functiei ![]() in
in ![]() ,
, ![]() punct de acumulare
pentru
punct de acumulare
pentru ![]() , se definesc astfel:
, se definesc astfel:
limita
la dreapta: ![]()
![]() a.i. oricare ar fi
punctul
a.i. oricare ar fi
punctul ![]() , cu
, cu ![]() sa avem
sa avem ![]() .
.
limita la stanga: ![]()
![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() , cu
, cu ![]() sa avem
sa avem ![]() .
.
Propozitie. Fie![]() o functie reala de o variabila reala
si
o functie reala de o variabila reala
si ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() . Daca limita functiei
. Daca limita functiei ![]() in punctul
in punctul ![]() exista, atunci
aceasta limita este unica.
exista, atunci
aceasta limita este unica.
Demonstratie. Daca ![]() are limita
are limita ![]() in punctul
in punctul ![]() , atunci oricare ar fi sirul
, atunci oricare ar fi sirul ![]() ,
, ![]() , avem
, avem ![]() , deci toate sirurile
, deci toate sirurile ![]() au limita unica
au limita unica ![]() .
.
5. Propozitie.
(1). Daca ![]() atunci
atunci ![]() ;
;
(2). Daca ![]() atunci
atunci ![]() (deoarece daca
(deoarece daca
![]() );
);
(3). Daca ![]() atunci este posibil ca
atunci este posibil ca
![]() sa nu existe;
sa nu existe;
Exemple: (a).
![]() nu exista, dar
nu exista, dar ![]() ; (b).
; (b).
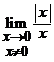 nu exista, dar
nu exista, dar 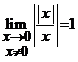 .
.
6. Observatie.
Fie ![]() si
si ![]() . Atunci cand dorim sa punem in evidenta unele
informatii despre comportarea acestor functii in punctul
. Atunci cand dorim sa punem in evidenta unele
informatii despre comportarea acestor functii in punctul ![]() , folosim uneori
notatiile:
, folosim uneori
notatiile:
). ![]() (citim: functiile
(citim: functiile ![]() si
si ![]() sunt asimptotic echivalente cand
sunt asimptotic echivalente cand ![]() ) daca si numai daca
) daca si numai daca
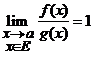 .
.
). ![]() (citim: functia
(citim: functia ![]() are un ordin mai mic
decat functia
are un ordin mai mic
decat functia ![]() , cand
, cand ![]() ) daca si numai daca
) daca si numai daca 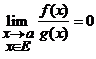 .
.
). ![]() (citim: functia
(citim: functia ![]() are acelasi ordin cu functia
are acelasi ordin cu functia ![]() , cand
, cand ![]() ) daca si numai daca
) daca si numai daca
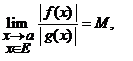 unde
unde ![]() este o
este o ![]() .
.
Evident, in aceste definitii admitem
ca ambele functii ![]() sunt bine definite
intr-o vecinatate
sunt bine definite
intr-o vecinatate ![]() si diferite de
zero in orice
si diferite de
zero in orice ![]() , exceptand eventual cazul
, exceptand eventual cazul ![]() .
.
Exemple:
) ![]() deoarece
deoarece ![]() .
.
) ![]() deoarece
deoarece 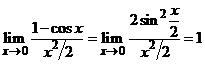 .
.
) ![]() . 4)
. 4) ![]() .
.
) ![]() . 6)
. 6) ![]() .
.
Functii reale continue de o variabila reala
7. Definitie. Fie ![]() o functie
reala de o variabila reala si
o functie
reala de o variabila reala si ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() . Spunem ca functia
. Spunem ca functia ![]() este continua in punctul
este continua in punctul ![]() daca limita
lui
daca limita
lui ![]() in
in ![]() este egala cu
este egala cu ![]() ,
,
![]() .
.
8. Teorema. (caracterizarea
continuitatii intr-un punct). Fie ![]() si
si ![]() un punct de acumulare
pentru
un punct de acumulare
pentru ![]() . Urmatoarele afirmatii sunt echivalente:
. Urmatoarele afirmatii sunt echivalente:
functia ![]() este continua in punctul
este continua in punctul ![]() ;
;
pentru orice vecinatate ![]() exista o
vecinatate
exista o
vecinatate ![]() a.i.
a.i. ![]() ;
;
(3). ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() , cu
, cu ![]() sa avem
sa avem ![]() ;
;
oricare ar fi sirul ![]() de puncte din
de puncte din ![]() si
si ![]() sa avem
sa avem ![]() ;
;
(5). oricare ar fi vecinatatea ![]() atunci
atunci ![]() este o vecinatate
a lui
este o vecinatate
a lui ![]() inclusa in
inclusa in ![]() ; altfel spus, functia
; altfel spus, functia ![]() intoarce
vecinatatile din
intoarce
vecinatatile din ![]() ale lui
ale lui ![]() in
vecinatati ale lui
in
vecinatati ale lui ![]() din
din ![]() .
.
Functia ![]() se numeste continua
pe
se numeste continua
pe ![]() daca si
numai daca este continua in orice punct din
daca si
numai daca este continua in orice punct din ![]() .
.
Functia ![]() este continua pe
este continua pe ![]() , daca si numai daca oricare ar fi
multimea deschisa
, daca si numai daca oricare ar fi
multimea deschisa ![]() ,
,
atunci ![]() este multime
deschisa in
este multime
deschisa in ![]() (definitia
globala a continuitatii).
(definitia
globala a continuitatii).
Daca ![]() nu este continua
in punctul
nu este continua
in punctul ![]() , atunci spunem ca
, atunci spunem ca ![]() este discontinua in
este discontinua in ![]() sau ca punctul
sau ca punctul ![]() este punct de discontinuitate pentru
este punct de discontinuitate pentru ![]() . Deoarece
. Deoarece ![]() este continua in
punctele izolate ale lui
este continua in
punctele izolate ale lui ![]() , atunci orice punct de discontinuitate
, atunci orice punct de discontinuitate ![]() al lui
al lui ![]() este punct de
acumulare pentru
este punct de
acumulare pentru ![]() si evident
si evident ![]() .
.
9. Observatie. Daca un punct ![]() nu apartine
domeniului de definitie al lui
nu apartine
domeniului de definitie al lui ![]() , atunci nu are sens sa se puna problema
continuitatii sau discontinuitatii in acest punct, chiar
daca
, atunci nu are sens sa se puna problema
continuitatii sau discontinuitatii in acest punct, chiar
daca ![]() este punct de
acumulare pentru domeniul de definitie al lui
este punct de
acumulare pentru domeniul de definitie al lui ![]() .
.
Daca ![]() este discontinua
in punctul
este discontinua
in punctul ![]() si exista
limite laterale
si exista
limite laterale ![]() si
si ![]() , finite si
, finite si ![]() , atunci
, atunci ![]() este punct de discontinuitate de speta intai.
In acest caz diferenta
este punct de discontinuitate de speta intai.
In acest caz diferenta
![]() , (1)
, (1)
se numeste saltul lui ![]() in
in ![]() .
.
In caz contrar, punctul ![]() se numeste punct de discontinuitate de a doua speta.
se numeste punct de discontinuitate de a doua speta.
Functia ![]() se numeste continua la stanga (respectiv, continua la dreapta) in
se numeste continua la stanga (respectiv, continua la dreapta) in ![]() , daca
, daca ![]() (respectiv
(respectiv ![]() . Asadar, rezulta ca functia
. Asadar, rezulta ca functia ![]() este continua in
este continua in ![]() daca si
numai daca exista limitele laterale ale lui
daca si
numai daca exista limitele laterale ale lui ![]() in
in ![]() si avem
si avem ![]() .
.
10.
Definitie. Fie ![]() , doua multimi si functia
, doua multimi si functia ![]() . Spunem ca functia
. Spunem ca functia ![]() realizeaza un omeomorfism de la
realizeaza un omeomorfism de la ![]() la
la ![]() , daca se verifica conditiile:
, daca se verifica conditiile:
functia ![]() este bijectiva;
este bijectiva;
functia ![]() si functia inversa
si functia inversa ![]() sunt functii
continue.
sunt functii
continue.
11.
Curbe si suprafete Jordan. Fie ![]() un spatiu
euclidian n-dimensional (
un spatiu
euclidian n-dimensional (![]() ) si segmentul
) si segmentul ![]() al axei reale. Daca
s-a stabilit un omeomorfism intre
segmentul
al axei reale. Daca
s-a stabilit un omeomorfism intre
segmentul ![]() si o
submultime
si o
submultime ![]() ,
, ![]() , atunci spunem ca
, atunci spunem ca ![]() este un arc de curba simpla Jordan;
imaginea punctelor
este un arc de curba simpla Jordan;
imaginea punctelor ![]() si
si ![]() prin omeomorfismul
prin omeomorfismul ![]() se numesc extremitatile curbei
se numesc extremitatile curbei ![]() .
.
Presupunem ca s-a ales o baza in ![]() , astfel incat orice punct
, astfel incat orice punct ![]() este reprezentat prin
coordonatele sale
este reprezentat prin
coordonatele sale ![]() ,
, ![]() si ca aceste
coordonate sunt functii continue de variabila
si ca aceste
coordonate sunt functii continue de variabila ![]() si la orice
valoare
si la orice
valoare ![]() corespunde un unic
punct
corespunde un unic
punct ![]() si numai unul.
Daca s-a realizat o astfel de corespondenta spunem ca s-a
dat o reprezentare parametrica a
lui
si numai unul.
Daca s-a realizat o astfel de corespondenta spunem ca s-a
dat o reprezentare parametrica a
lui ![]() ; reprezentarea parametrica induce pe curba o anumita
orientare. Astfel de reprezentari nu afirma nimic despre netezimea
curbei
; reprezentarea parametrica induce pe curba o anumita
orientare. Astfel de reprezentari nu afirma nimic despre netezimea
curbei ![]() . Corespondenta intre punctele intervalului
. Corespondenta intre punctele intervalului ![]() si submultimea
si submultimea
![]() este biunivoca cu
exceptia a doua cazuri care pot fi intalnite:
este biunivoca cu
exceptia a doua cazuri care pot fi intalnite:
Punctul ![]() este imaginea prin
este imaginea prin ![]() a doua valori
diferite
a doua valori
diferite ![]() ,
, ![]() (interioare intervalul
(interioare intervalul
![]() ), caz in care
), caz in care ![]() se numeste punct dublu.
se numeste punct dublu.
Punctul ![]() este numai intr-o
singura situatie imaginea prin
este numai intr-o
singura situatie imaginea prin ![]() a doua valorilor
diferite, anume
a doua valorilor
diferite, anume ![]() si
si ![]() (
(![]() ), caz in care
), caz in care ![]() se numeste curba simpla inchisa.
se numeste curba simpla inchisa.
Fie ![]() o curba
plana (
o curba
plana (![]() ). Daca
). Daca ![]() este curba
simpla inchisa atunci ea imparte planul in doua regiuni, una interioara si alta exterioara a.i. curba
este curba
simpla inchisa atunci ea imparte planul in doua regiuni, una interioara si alta exterioara a.i. curba ![]() este frontiera lor
comuna.
este frontiera lor
comuna.
Fie ![]() un domeniu. Daca
un domeniu. Daca ![]() este un omeomorfism,
atunci submultimea
este un omeomorfism,
atunci submultimea ![]() se numeste suprafata jordaniana.
se numeste suprafata jordaniana.
Exemple.
(1). Functia ![]() , definita prin
, definita prin ![]() este un omeomorfism de la intervalul
este un omeomorfism de la intervalul ![]() la intervalul
la intervalul ![]() si functia
inversa
si functia
inversa ![]() , este definita prin
, este definita prin
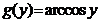 , oricare ar fi
, oricare ar fi ![]() .
.
Fie functia ![]() , definita prin
, definita prin ![]() ,
, ![]() . Vom nota cu
. Vom nota cu ![]() si
si ![]() functiile coordonate ale lui
functiile coordonate ale lui ![]() . Atunci
. Atunci
(1). ![]() este functie
continua;
este functie
continua;
(2). ![]() si
si ![]() , unde
, unde ![]() este cercul trigonometric.
este cercul trigonometric.
(3). ![]() este functie
injectiva pe
este functie
injectiva pe ![]() si pe
si pe ![]() , adica restrictiile
, adica restrictiile ![]() si
si ![]() sunt functii
injective si corespondenta prin
sunt functii
injective si corespondenta prin ![]() intre
intre ![]() si cercul
trigonometric este omeomorfism.
si cercul
trigonometric este omeomorfism.
Demonstratie. (1). Fie proiectiile canonice, ![]() ,
, ![]() , definite prin
, definite prin ![]() si
si ![]() si functiile
si functiile
![]() . Atunci
. Atunci ![]() continua si
derivabila daca si numai daca proiectiile
continua si
derivabila daca si numai daca proiectiile ![]() sunt functii
continue si derivabile. Punem
sunt functii
continue si derivabile. Punem ![]() , unde
, unde ![]() si
si ![]() .
.
(2). Aratam incluziunea![]() . Fie
. Fie ![]() , atunci exista
, atunci exista ![]() astfel incat sa
avem
astfel incat sa
avem ![]() . Deci,
. Deci, ![]() ,
, ![]() si atunci
si atunci ![]() , de unde rezulta ca
, de unde rezulta ca ![]() .
.
Pentru a arata incluziunea ![]() , fie
, fie ![]() oarecare si
oarecare si ![]() . Atunci
. Atunci ![]() si avem
si avem ![]() si
si ![]() .
.
Definim ![]() . Atunci, din relatia
. Atunci, din relatia ![]() obtinem ca
obtinem ca ![]() , de unde rezulta
, de unde rezulta ![]() .
.
Avem situatiile:
(i). daca ![]() atunci
atunci ![]() ;
;
(ii).
daca ![]() atunci
atunci ![]() ; asadar,
; asadar, ![]() .
.
Perechea ![]() , formata din: parametrizarea
, formata din: parametrizarea ![]() ,
, ![]() si imaginea din
si imaginea din ![]() a parametrizarii,
a parametrizarii, ![]() , se numeste drum
parametrizat din
, se numeste drum
parametrizat din ![]() .
.
12. Observatie. Continuitatea unei functii este o notiune punctuala, ea depinde de fiecare punct in care este definita functia.
In continuare vom defini notiunea de uniform continuitate, care depinde de intreaga multime pe care este definita functia.
13.
Definitie. Fie ![]() , o multime care nu contine puncte izolate si
, o multime care nu contine puncte izolate si ![]() o functie. Spunem ca functia
o functie. Spunem ca functia ![]() este uniform
continua pe
este uniform
continua pe ![]() , daca
, daca
![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() , cu
, cu ![]() sa avem
sa avem ![]() ;
;
Se demonstreaza imediat, afirmatiile:
O functie uniform continua pe ![]() este continua pe
este continua pe ![]() .
.
Daca functia ![]() este lipschitziana pe
este lipschitziana pe ![]() , adica,
, adica,
daca
exista ![]() a.i.
a.i. ![]() , oricare ar fi
, oricare ar fi ![]() ,
,
atunci ![]() este uniform
continua pe
este uniform
continua pe ![]() (se alege
(se alege ![]() ).
).
functia ![]() nu este uniform continua pe
nu este uniform continua pe ![]() daca si
numai daca
daca si
numai daca ![]() cu proprietatea ca
cu proprietatea ca
![]() exista doua puncte din
exista doua puncte din ![]() , fie acestea
, fie acestea ![]() si
si ![]() , a.i.
, a.i. ![]()
![]() .
.
1 Teorema lui Weierstrass . Fie ![]() , o multime compacta si
, o multime compacta si ![]() o functie
continua pe
o functie
continua pe ![]() , atunci functia
, atunci functia ![]() este marginita
si isi atinge marginile
(altfel spus
este marginita
si isi atinge marginile
(altfel spus ![]() este multime
compacta.
este multime
compacta.
Demonstratie. Aratam ca ![]() este
marginita. Presupunem prin absurd ca
este
marginita. Presupunem prin absurd ca![]() nu este marginita pe
nu este marginita pe ![]() si, pentru a fixa
ideile vom presupune ca
si, pentru a fixa
ideile vom presupune ca ![]() nu este
marginita superior. Atunci exista un sir
nu este
marginita superior. Atunci exista un sir ![]() de puncte din
de puncte din ![]() , cu proprietatea ca sirul
, cu proprietatea ca sirul ![]() . Cum sirul
. Cum sirul ![]() este continut in
este continut in ![]() care este
marginita, rezulta ca este marginit, deci contine
un subsir
care este
marginita, rezulta ca este marginit, deci contine
un subsir ![]() care este convergent
(lema lui Cesaró) catre punctul
care este convergent
(lema lui Cesaró) catre punctul ![]() (multime
inchisa). Deoarece
(multime
inchisa). Deoarece ![]() este continua pe
este continua pe ![]() , atunci este continua in
, atunci este continua in ![]() si putem scrie
ca
si putem scrie
ca ![]() . Pe de alta parte, subsirul
. Pe de alta parte, subsirul ![]() , al sirului
, al sirului ![]() care este convergent
si tinde la
care este convergent
si tinde la ![]() , va tinde catre
, va tinde catre ![]() . Asadar, avem
. Asadar, avem ![]() ceea ce contrazice
faptul ca
ceea ce contrazice
faptul ca ![]() ia valori in
ia valori in ![]() , deci
, deci ![]() este
marginita superior. Analog se arata si marginirea
inferioara a lui
este
marginita superior. Analog se arata si marginirea
inferioara a lui ![]() . In consecinta, exista
. In consecinta, exista ![]() , a.i.
, a.i. ![]() ,
, ![]() . Desigur,
. Desigur, ![]() si
si ![]() . Aratam ca exista
. Aratam ca exista ![]() , a.i.
, a.i. ![]() si respectiv
si respectiv ![]() . Vom arata prima afirmatie, adica exista
. Vom arata prima afirmatie, adica exista
![]() a.i.
a.i. ![]() . Intr-adevar, in caz contrar, am avea
. Intr-adevar, in caz contrar, am avea ![]() , oricare ar fi
, oricare ar fi ![]() . Fie functia
. Fie functia ![]() , definita prin
, definita prin ![]() . Atunci
. Atunci ![]() este functie continua
pe
este functie continua
pe ![]() si ia valori
pozitive. Asadar,
si ia valori
pozitive. Asadar, ![]() este marginita
pe
este marginita
pe ![]() , adica exista
, adica exista ![]() a.i.
a.i. ![]() , oricare ar fi
, oricare ar fi ![]() .
.
Rezulta ca ![]() , ceea ce contrazice faptul ca
, ceea ce contrazice faptul ca ![]() este cel mai mare
minorant .
este cel mai mare
minorant .
15. Observatie.
Daca multimea ![]() nu este inchisa,
dar este marginita, atunci
nu este inchisa,
dar este marginita, atunci ![]() nu este neaparat
marginita, sau daca este marginita, nu isi atinge
marginile. De exemplu, functia
nu este neaparat
marginita, sau daca este marginita, nu isi atinge
marginile. De exemplu, functia ![]() , definita prin
, definita prin ![]() , este continua si marginita pe
, este continua si marginita pe ![]() , insa nu isi atinge marginea superioara care
este egala cu
, insa nu isi atinge marginea superioara care
este egala cu ![]() si nici marginea
inferioara care este egala cu
si nici marginea
inferioara care este egala cu ![]() . Functia
. Functia ![]() , definita prin
, definita prin ![]() , este continua pe
, este continua pe ![]() si nu este
marginita superior, pentru ca
si nu este
marginita superior, pentru ca ![]() .
.
16. Teorema lui Heine.
Fie ![]() , o multime compacta si
, o multime compacta si ![]() o functie
continua pe
o functie
continua pe ![]() , atunci functia
, atunci functia ![]() este uniform continua pe
este uniform continua pe ![]() .
.
Demonstratie. Multimea ![]() este compacta
este compacta ![]() este multime inchisa
si marginita. Vom presupune ca
este multime inchisa
si marginita. Vom presupune ca ![]() nu este uniform continua pe
nu este uniform continua pe ![]() . Atunci exista
. Atunci exista ![]() cu proprietatea
ca oricare ar fi
cu proprietatea
ca oricare ar fi ![]() , in particular alegem
, in particular alegem ![]()
![]() , exista doua puncte din
, exista doua puncte din ![]() , fie acestea
, fie acestea ![]() si
si ![]() , a.i.
, a.i. ![]()
![]() . Cum multimea
. Cum multimea ![]() este
marginita, atunci sirul
este
marginita, atunci sirul ![]() este marginit,
deci contine un subsir convergent, fie acesta
este marginit,
deci contine un subsir convergent, fie acesta ![]() si,
si, ![]() . Deoarece
. Deoarece ![]() este punct aderent pentru
multimea
este punct aderent pentru
multimea ![]() a termenilor
sirului, deci pentru
a termenilor
sirului, deci pentru ![]() si, cum
si, cum ![]() este inchisa,
atunci
este inchisa,
atunci ![]() . Deoarece
. Deoarece ![]() este continua in
este continua in ![]() avem
avem ![]() . Analog se arata ca exista
. Analog se arata ca exista ![]() , a.i.
, a.i. ![]() si
si ![]() si cum
si cum ![]() , atunci prin trecere la limita rezulta ca
, atunci prin trecere la limita rezulta ca ![]() si deci
si deci ![]() .
.
Deoarece ![]() este continua in
este continua in ![]() atunci putem
scrie
atunci putem
scrie ![]() si
si ![]() . Din relatia
. Din relatia
![]() ,
,
deducem ca ![]() si deci diferenta
si deci diferenta
![]() devine suficient de
mica dorim. Asadar, de la un anumit rang incolo, avem
devine suficient de
mica dorim. Asadar, de la un anumit rang incolo, avem ![]() , ceea ce este in contradictie cu presupunerea
facuta.
, ceea ce este in contradictie cu presupunerea
facuta.
17. Criteriul lui Cauchy de la siruri (teorema 2.9 si propozitia 2.20), care stabileste conditia de existenta a limitei finite a unui sir de numere reale dat, conduce la urmatorul criteriu pentru functii:
Criteriul
lui Cauchy. Fie ![]() ,
, ![]() punct de acumulare
pentru
punct de acumulare
pentru ![]() situat la
distanta finita. Conditia necesara si
suficienta ca functia
situat la
distanta finita. Conditia necesara si
suficienta ca functia ![]() sa aiba
limita finita in punctul
sa aiba
limita finita in punctul ![]() este ca pentru orice
este ca pentru orice ![]() sa existe o
vecinatate
sa existe o
vecinatate ![]() a.i. pentru orice
a.i. pentru orice ![]() , sa avem
, sa avem ![]() .
.
Demonstratie. "![]() ". Presupunem ca exista finita limita
". Presupunem ca exista finita limita ![]() ,
, ![]() . Atunci pentru orice
. Atunci pentru orice ![]() , exista
, exista ![]() a.i. pentru orice
a.i. pentru orice ![]() ,
, ![]() cu
cu ![]() implica
implica ![]() . Fie
. Fie ![]() oarecare, a.i.
oarecare, a.i. ![]() si
si ![]() ,
, ![]() . Atunci avem
. Atunci avem
![]() .
.
"![]() ". Fie
". Fie ![]() dat. Presupunem
ca exista
dat. Presupunem
ca exista ![]() a.i.
a.i. ![]() , pentru toate punctele
, pentru toate punctele ![]() cu proprietatea
ca
cu proprietatea
ca ![]() ,
, ![]() . Fie un sir particular
. Fie un sir particular ![]() din
din ![]() care converge
catre punctul de acumulare
care converge
catre punctul de acumulare ![]() . Vom studia sirul
. Vom studia sirul ![]() al valorilor
sirului ales
al valorilor
sirului ales ![]() .
.
Deoarece ![]() este dat si
este dat si ![]() este functie de
este functie de ![]() bine determinata,
atunci putem alege numarul natural
bine determinata,
atunci putem alege numarul natural ![]() a.i. sa avem
a.i. sa avem
![]() si
si ![]() , pentru orice
, pentru orice ![]() .
.
Dar atunci rezulta ca ![]() si, in
consecinta, sirul
si, in
consecinta, sirul ![]() este un sir
Cauchy de numere reale, deci convergent catre o limita finita
este un sir
Cauchy de numere reale, deci convergent catre o limita finita ![]() .
.
Alegem ![]() a.i.
a.i. ![]() si cum
si cum ![]() , pentru orice
, pentru orice ![]() , atunci pe baza ipotezei facute, putem scrie
, atunci pe baza ipotezei facute, putem scrie ![]() . De aici deducem
. De aici deducem
![]()
ceea ce arata ca de indata ce ![]() implica
implica ![]() si deci
si deci ![]() tinde catre
limita
tinde catre
limita ![]() .
.
Exercitiu. Aratati ca functia ![]() , are limita in vecinatatea originii.
, are limita in vecinatatea originii.
R. Vom arata ca este
satisfacut criteriul lui Cauchy in vecinatatea originii. In acest
scop, fie ![]() si
si ![]() . Avem
. Avem ![]() .
.
Fie ![]() oarecare, dar fixat.
Este suficient sa alegem
oarecare, dar fixat.
Este suficient sa alegem ![]() astfel ca de
indata ce
astfel ca de
indata ce ![]() si
si ![]() implica
implica ![]() .
.
Deoarece ![]() , atunci
, atunci ![]() si deci,
si deci, ![]() .
.
18.
Teorema Cauchy-Bolzano. Fie ![]() un interval si
un interval si ![]() o functie
continua pe
o functie
continua pe ![]() . Atunci
. Atunci ![]() este un interval din
este un interval din ![]() .
.
Demonstratie. Daca ![]() nu se reduce la un
punct, fie
nu se reduce la un
punct, fie ![]() si
si ![]() cu
cu ![]() , doua puncte distincte din
, doua puncte distincte din ![]() . Aratam ca
. Aratam ca ![]() . Fie
. Fie 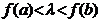 si functia
si functia ![]() ,
, ![]() . Deoarece
. Deoarece ![]() este continua pe
este continua pe ![]() iar
iar ![]() si
si ![]() . Atunci exista un punct
. Atunci exista un punct ![]() intre
intre ![]() si
si ![]() a.i.
a.i. ![]() si deci,
exista
si deci,
exista ![]() intre
intre ![]() si
si ![]() astfel incat
astfel incat ![]() .
.
Pentru a arata existenta punctului ![]() intre
intre ![]() si
si ![]() a.i.
a.i. ![]() , vom considera multimea nevida
, vom considera multimea nevida ![]() . Fie
. Fie ![]() (exista
(exista ![]() cu aceasta
proprietate deoarece multimea
cu aceasta
proprietate deoarece multimea ![]() este
marginita superior). Cum
este
marginita superior). Cum ![]() , daca
, daca ![]() atunci exista un
interval centrat in
atunci exista un
interval centrat in ![]() pe care
pe care ![]() , dar acest fapt vine in contradictie cu
, dar acest fapt vine in contradictie cu ![]() . Daca
. Daca ![]() ajungem din nou la
contradictie deoarece
ajungem din nou la
contradictie deoarece ![]() . Asadar, ramane unica posibilitatea
. Asadar, ramane unica posibilitatea ![]() .
.
Din teorema 18 deducem ca
orice functie reala ![]() , definita si continua pe un interval compact
, definita si continua pe un interval compact ![]() , ia toate valorile intermediare cuprinse intre margini.
, ia toate valorile intermediare cuprinse intre margini.
19.
Teorema. Daca ![]() este omeomorfism
si
este omeomorfism
si ![]() este multime
compacta atunci
este multime
compacta atunci ![]() este multime
compacta.
este multime
compacta.
Demonstratie.
Fie ![]() o submultime
oarecare (
o submultime
oarecare (![]() are o infinitate de elemente). Deoarece
are o infinitate de elemente). Deoarece ![]() este omeomorfism intre
este omeomorfism intre
![]() si
si ![]() , atunci exista
, atunci exista ![]() (
(![]() are o infinitate de elemente) a. i.
are o infinitate de elemente) a. i. ![]() . Cum multimea
. Cum multimea ![]() este compacta,
atunci
este compacta,
atunci ![]() poseda un punct
de acumulare
poseda un punct
de acumulare ![]() . Asadar, exista in
. Asadar, exista in ![]() , un sir
, un sir ![]() care converge
catre
care converge
catre ![]() . Fie sirul
. Fie sirul ![]() si
si ![]() din
din ![]() . Deoarece
. Deoarece ![]() este functie
continua atunci din
este functie
continua atunci din ![]() (cand
(cand ![]() ) rezulta ca
) rezulta ca ![]() . Asadar, multimea infinita
. Asadar, multimea infinita ![]() , fiind aleasa oarecare, poseda un punct de
acumulare si deci
, fiind aleasa oarecare, poseda un punct de
acumulare si deci ![]() este compacta.
este compacta.
Oscilatia unei functii
20. Fie ![]() un spatiu metric si
un spatiu metric si ![]() o multime
oarecare. Definim diametrul
multimii
o multime
oarecare. Definim diametrul
multimii ![]() , notat cu
, notat cu ![]() sau
sau ![]() , cu ajutorul numarului
, cu ajutorul numarului
![]() .
.
Numarul ![]() se numeste distanta de la punctul
se numeste distanta de la punctul ![]() la multimea
la multimea ![]() .
.
Daca ![]() este multime
inchisa atunci
este multime
inchisa atunci ![]() .
.
Fie functia ![]() . Diametrul multimii
. Diametrul multimii ![]() , se numeste oscilatia
functiei
, se numeste oscilatia
functiei ![]() pe multimea
pe multimea ![]() si se
noteaza prin
si se
noteaza prin
![]() .
.
Daca ![]() este un punct oarecare din
este un punct oarecare din ![]() si
si ![]() multimea
vecinatatilor lui
multimea
vecinatatilor lui ![]() , atunci numarul
, atunci numarul
![]() ,
,
defineste oscilatia lui
![]() in punctul
in punctul ![]() .
.
21.
Propozitie. Fie
functia ![]() . Atunci avem
. Atunci avem
(1). Oscilatia ![]() este finita
daca si numai daca
este finita
daca si numai daca ![]() este marginita pe
este marginita pe ![]() si avem
si avem
![]() .
.
(2). Daca ![]() .
.
22. Propozitie. Fie functia ![]() si
si ![]() . Urmatoarele afirmatii sunt echivalente:
. Urmatoarele afirmatii sunt echivalente:
(1). functia ![]() este continua
intr-un punctul
este continua
intr-un punctul ![]() ;
;
(2). oscilatia functiei ![]() in punctul
in punctul ![]() este nula
(adica
este nula
(adica ![]() );
);
(3). ![]() .
.
Solutie. "(1)![]() (2)". Presupunem ca
(2)". Presupunem ca ![]() este continua in
este continua in ![]() . Atunci oricare ar fi
. Atunci oricare ar fi ![]() ,
, ![]() a.i. pentru orice
a.i. pentru orice ![]() cu
cu ![]() sa implice
sa implice 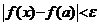 . Asadar, fiind dat
. Asadar, fiind dat ![]() , exista o vecinatate a lui
, exista o vecinatate a lui ![]() ,
, ![]() a.i. oricare ar fi
a.i. oricare ar fi ![]() sa avem
sa avem 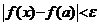 . De aici rezulta ca
. De aici rezulta ca ![]() si
si ![]() si in
consecinta avem
si in
consecinta avem ![]() de unde obtinem
ca
de unde obtinem
ca ![]() . Cum numarul
. Cum numarul ![]() a fost ales arbitrar
rezulta ca
a fost ales arbitrar
rezulta ca ![]() .
.
"(2)![]() (1)". Presupunem ca
(1)". Presupunem ca ![]() . Atunci
. Atunci ![]() a.i.
a.i. ![]() . De aici deducem ca
. De aici deducem ca ![]() , de unde obtinem:
, de unde obtinem:![]() , ceea ce arata ca
, ceea ce arata ca ![]() este continua in
este continua in ![]() .
.
Echivalenta ![]() se verifica
imediat.
se verifica
imediat.
Functii continue pe portiuni. Functii etajate. Functii netede pe portiuni
23.
Definitie. Fie ![]() un spatiu metric
si
un spatiu metric
si ![]() un interval inchis al
axei reale. Functia
un interval inchis al
axei reale. Functia ![]() se zice continua
pe portiuni (continua pe
bucati) daca exista o partitie finita
(diviziune finita)
se zice continua
pe portiuni (continua pe
bucati) daca exista o partitie finita
(diviziune finita) ![]() a lui
a lui ![]() si
aplicatiile continue
si
aplicatiile continue ![]() , unde
, unde ![]() , a.i.
, a.i. ![]() , adica sa avem
, adica sa avem ![]() , pentru orice
, pentru orice ![]() .
.
Altfel spus, functia ![]() este continua pe
portiuni daca este continua in orice punct din
este continua pe
portiuni daca este continua in orice punct din ![]() cu exceptia unui
numar finit de puncte, iar in aceste puncte exista limitele laterale
ale lui
cu exceptia unui
numar finit de puncte, iar in aceste puncte exista limitele laterale
ale lui ![]() . Asadar, multimea punctelor de discontinuitate
. Asadar, multimea punctelor de discontinuitate ![]() ale lui
ale lui ![]() este finita
si acestea sunt puncte de discontinuitate
de prima speta (exista si sunt finite limitele laterale
este finita
si acestea sunt puncte de discontinuitate
de prima speta (exista si sunt finite limitele laterale![]() si
si ![]() ). Este clar ca in
). Este clar ca in ![]() nu exista
nu exista ![]() , iar in
, iar in ![]() nu exista
nu exista ![]() .
.
2 Definitie.
Functia ![]() , se zice etajata
(functie in scara)
daca exista o partitie
finita (o diviziune finita)
, se zice etajata
(functie in scara)
daca exista o partitie
finita (o diviziune finita)
![]() a lui
a lui ![]() a.i.
a.i. ![]() , unde
, unde ![]() sunt constante,
sunt constante, ![]() ; altfel spus, sa avem
; altfel spus, sa avem ![]() , pentru orice
, pentru orice ![]() ,
, ![]() .
.
2 Observatie.
Functia etajata ia un numar finit de valori, ![]() ; Orice functie etajata, care ia valori finite, se
poate scrie sub forma
; Orice functie etajata, care ia valori finite, se
poate scrie sub forma
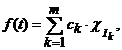
unde 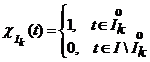 , este functia
caracteristica a intervalului
, este functia
caracteristica a intervalului ![]() .
.
Daca una sau mai multe din constantele ![]() iau valorile
iau valorile ![]() sau
sau ![]() , formula de mai sus ramane valabila daca se
face conventia
, formula de mai sus ramane valabila daca se
face conventia ![]() .
.
25.
Propozitie. Multimea
functiilor etajate pe ![]() formeaza un
spatiu vectorial peste corpul
formeaza un
spatiu vectorial peste corpul ![]() al numerelor reale.
al numerelor reale.
Demonstratie. Fie 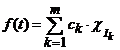 si
si ![]() , atunci avem
, atunci avem 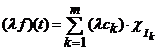 , deci
, deci ![]() este functie
etajata.
este functie
etajata.
Fie ![]() doua functii
etajate. Atunci exista doua partitii finite ale lui
doua functii
etajate. Atunci exista doua partitii finite ale lui ![]() , fie acestea
, fie acestea ![]() si
si ![]() a.i.
a.i. ![]() ia valorile
ia valorile ![]() pe
pe ![]() si
si ![]() ia valorile
ia valorile ![]() pe
pe ![]() . Deci, putem scrie
. Deci, putem scrie 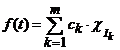 si
si 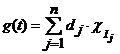 . Deoarece
. Deoarece ![]() este fie multimea
vida, fie un interval din
este fie multimea
vida, fie un interval din ![]() si atunci,
si atunci, ![]() este o partitie
finita a lui
este o partitie
finita a lui ![]() . Asadar,
. Asadar, ![]() ia valori constante pe
fiecare din intervalele partitiei
ia valori constante pe
fiecare din intervalele partitiei ![]() si avem
si avem
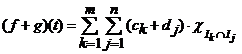
deci, ![]() este functie
etajata. Evident, daca este cazul, se face conventia de calcul
este functie
etajata. Evident, daca este cazul, se face conventia de calcul ![]() .
.
26.
Propozitia. Produsul a
doua functii etajate pe ![]() este o functie
etajata.
este o functie
etajata.
Intr-adevar, fie 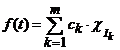 si
si 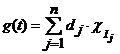 , atunci
, atunci ![]() formeaza o
partitie a lui
formeaza o
partitie a lui ![]() si putem scrie
si putem scrie
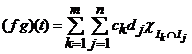 .
.
Din cele doua propozitii
rezulta ca multimea functiilor etajate pe ![]() formeaza o algebra de functii.
formeaza o algebra de functii.
27. Definitie. Functia ![]() ,
, ![]() spatiu metric, se
zice neteda pe portiuni (neteda pe bucati)
daca exista o diviziune
spatiu metric, se
zice neteda pe portiuni (neteda pe bucati)
daca exista o diviziune ![]() a lui
a lui ![]() si functiile
si functiile
![]() ,
, ![]() ,
, ![]() , a.i.
, a.i. ![]() , adica sa avem
, adica sa avem ![]() , pentru orice
, pentru orice ![]() .
.
Daca ![]() este neteda pe
portiuni, atunci
este neteda pe
portiuni, atunci ![]() este
diferentiabila in orice punct din
este
diferentiabila in orice punct din ![]() si in orice punct
si in orice punct
![]() exista si
sunt finite derivatele laterale
exista si
sunt finite derivatele laterale ![]() si
si ![]() ), iar in
), iar in ![]() exista numai
exista numai ![]() si in
si in ![]() exista numai
exista numai ![]() si atunci
si atunci ![]() este definita
astfel:
este definita
astfel:
(i). ![]() este derivata lui
este derivata lui ![]() in orice
in orice ![]() , daca aceasta exista;
, daca aceasta exista;
(ii). ![]() ia valori arbitrare in
punctele
ia valori arbitrare in
punctele ![]() .
.
28. Observatie. Functiile continue pe portiuni, ![]() formeaza o algebra de functii.
formeaza o algebra de functii.
Exemplul
1. Fie intervalul ![]() si diviziunea
si diviziunea ![]() , care realizeaza o partitie finita a lui
, care realizeaza o partitie finita a lui ![]() si functia
etajata
si functia
etajata ![]() definita prin
(graficul este realizat cu programul Mathcad).
definita prin
(graficul este realizat cu programul Mathcad).
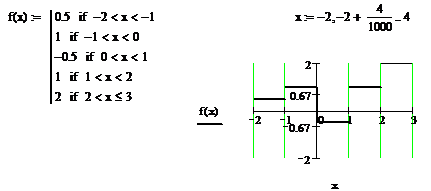
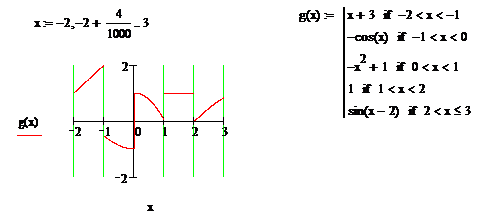
Exemplul
2. Fie ![]() si diviziunea
si diviziunea ![]() , care realizeaza o partitie finita a lui
, care realizeaza o partitie finita a lui ![]() . Functia
. Functia ![]() definita mai jos,
este neteda pe portiuni (graficul lui
definita mai jos,
este neteda pe portiuni (graficul lui ![]() este realizat cu
programul Mathcad).
este realizat cu
programul Mathcad).
Exemplul 3. Fie ![]() si functia
si functia ![]() , definita prin
, definita prin ![]() . Atunci
. Atunci ![]() este continua pe
este continua pe ![]() . Fie partitia
. Fie partitia ![]() si intervalele
si intervalele ![]() si
si ![]() Evident, functia
Evident, functia ![]() are derivate continue
pe
are derivate continue
pe ![]() si pe
si pe ![]() si avem
si avem ![]()
Spatii de functii. Algebre de functii
Fie ![]() si
si ![]() doua
multimi. Atunci notam cu
doua
multimi. Atunci notam cu ![]() multimea
functiilor
multimea
functiilor ![]() .
.
Daca ![]() si
si ![]() sunt doua
spatii metrice, atunci notam cu
sunt doua
spatii metrice, atunci notam cu ![]() multimea functiilor continue
multimea functiilor continue ![]() . Evident, avem
. Evident, avem ![]() .
.
29.
Definitie. Numim algebra (![]() -algebra)
orice inel
-algebra)
orice inel ![]() pe care s-a dat o
aplicatie
pe care s-a dat o
aplicatie ![]() , notata
, notata ![]() (inmultirea cu
scalari) a.i. sa se verifice proprietatile:
(inmultirea cu
scalari) a.i. sa se verifice proprietatile:
(i). ![]() este
este ![]() -spatiu vectorial
(grupul aditiv al inelului
-spatiu vectorial
(grupul aditiv al inelului ![]() este organizat ca
spatiu vectorial peste corpul
este organizat ca
spatiu vectorial peste corpul ![]() ).
).
(ii). iar inmultirea din
inelul ![]() verifica
conditia
verifica
conditia ![]() oricare ar fi
oricare ar fi ![]() si
si ![]() .
.
Algebra ![]() este comutativa (respectiv asociativa, cu unitate, cu divizori ai
lui zero), daca inelul
este comutativa (respectiv asociativa, cu unitate, cu divizori ai
lui zero), daca inelul ![]() este comutativ
respectiv asociativ, cu element unitate unitate, cu divizori ai lui zero).
este comutativ
respectiv asociativ, cu element unitate unitate, cu divizori ai lui zero).
Fie ![]() o algebra. Prin
definitie, baza spatiului vectorial
o algebra. Prin
definitie, baza spatiului vectorial ![]() este baza algebrei si dimensiunea
spatiului vectorial
este baza algebrei si dimensiunea
spatiului vectorial ![]() este dimensiunea algebrei.
este dimensiunea algebrei.
Exemplu. Fie ![]() o multime
nevida, atunci multimea
o multime
nevida, atunci multimea ![]() in care s-au definit
operatiile:
in care s-au definit
operatiile:
![]() (adunarea
functiilor
(adunarea
functiilor ![]() );
);
![]() (inmultirea functiilor
(inmultirea functiilor ![]() );
);
![]() ( inmultirea functiilor
( inmultirea functiilor ![]() cu scalari
cu scalari ![]() );
);
pentru orice ![]() si
si ![]() formeaza o algebra comutativa.
formeaza o algebra comutativa.
Fiind data o algebra ![]() , submultimea
, submultimea ![]() se numeste subalgebra a lui
se numeste subalgebra a lui ![]() , daca pentru orice
, daca pentru orice ![]() si
si ![]() avem
avem ![]() .
.
Numim algebra de functii pe
![]() orice subalgebra
orice subalgebra ![]() .
.
Exemplu. Fie ![]() un spatiu metric,
atunci
un spatiu metric,
atunci ![]() este algebra de functii.
este algebra de functii.
30. Definitie.
Orice algebra ![]() pe care s-a definit o
norma
pe care s-a definit o
norma ![]() , (
, (![]() este spatiu vectorial, deci are sens notiunea de
norma) care verifica proprietatea
este spatiu vectorial, deci are sens notiunea de
norma) care verifica proprietatea
![]() oricare ar fi
oricare ar fi ![]() ,
,
se numeste algebra normata.
O algebra normata si completa se numeste algebra Banach.
Exemple
(1). Daca ![]() este o multime, atunci multimea functiilor
marginite definite pe
este o multime, atunci multimea functiilor
marginite definite pe ![]() cu valori reale,
notata cu
cu valori reale,
notata cu ![]() , pe care s-a definit norma
, pe care s-a definit norma ![]() , este algebra Banach.
, este algebra Banach.
Daca![]() este spatiu metric compact, atunci
este spatiu metric compact, atunci ![]() este algebra
Banach.
este algebra
Banach.
Intr-adevar, daca ![]() este spatiu
metric compact, atunci orice functie continua
este spatiu
metric compact, atunci orice functie continua ![]() este uniform
continua;
este uniform
continua; ![]() , deci este algebra
de functii pe orice spatiu metric
, deci este algebra
de functii pe orice spatiu metric ![]() ; cu norma convergentei uniforme
; cu norma convergentei uniforme ![]() ,
, ![]() devine algebra
normata, deoarece putem scrie
devine algebra
normata, deoarece putem scrie
![]() .
.
Functii diferentiabile de o variabila reala
31.
Definitie. Fie ![]() un interval
nedegenerat,
un interval
nedegenerat, ![]() (
(![]() este punct interior intervalului
este punct interior intervalului ![]() ) si functia
) si functia ![]() . Spunem ca functia
. Spunem ca functia ![]() este derivabila in
este derivabila in ![]() daca si
numai daca exista si este
finita limita
daca si
numai daca exista si este
finita limita
![]() , notata cu
, notata cu ![]() ; (1)
; (1)
Numarul real ![]() se numeste derivata functiei
se numeste derivata functiei ![]() in punctul
in punctul ![]() .
.
Uneori, derivata functiei ![]() in punctul
in punctul ![]() va fi notata
prin
va fi notata
prin ![]() ; daca se folosesc notatiile
; daca se folosesc notatiile ![]() ,
, ![]() , atunci
, atunci ![]() si derivata
functiei
si derivata
functiei ![]() in punctul
in punctul ![]() este limita raportului
dintre "cresterea functiei
este limita raportului
dintre "cresterea functiei ![]() " si "cresterea
argumentului in jurul punctului
" si "cresterea
argumentului in jurul punctului ![]() ", cand
", cand ![]() .
.
Daca facem translatia ![]() , atunci din (5.1) obtinem (evident, daca
, atunci din (5.1) obtinem (evident, daca ![]() )
)
![]() ; (2)
; (2)
Daca functia ![]() este derivabila
in orice punct
este derivabila
in orice punct ![]() spunem ca
spunem ca ![]() este derivabila
pe
este derivabila
pe ![]() si datorita
relatiei (2) putem scrie
si datorita
relatiei (2) putem scrie
![]() , oricare ar fi
, oricare ar fi ![]() . (3)
. (3)
Daca ![]() si
si ![]() este derivabila
pe
este derivabila
pe ![]() , se mai scrie
, se mai scrie ![]() ; uneori, pentru a pune in evidenta argumentul in
raport cu care se face derivarea, se folosesc si notatiile
; uneori, pentru a pune in evidenta argumentul in
raport cu care se face derivarea, se folosesc si notatiile ![]() .
.
32.
Propozitie. Fie
functia ![]() . Daca functia
. Daca functia ![]() este derivabila
in punctul
este derivabila
in punctul ![]() atunci
atunci ![]() este continua in
este continua in ![]() .
.
Demonstratie. Deoarece functia este derivabila
in ![]() atunci limita (5.1)
exista si este finita. Trecand la limita relatia,
atunci limita (5.1)
exista si este finita. Trecand la limita relatia, ![]() , obtinem
, obtinem
![]()
deci, ![]() , care arata continuitatea functiei
, care arata continuitatea functiei ![]() in punctul
in punctul ![]() .
.
Reciproca acestei propozitii, in
general, este falsa. De exemplu, functia ![]() , definita prin
, definita prin
![]() nu este
derivabila in
nu este
derivabila in ![]() .
.
Derivabilitatea acestei functii depinde
de existenta limitei raportului ![]() in punctul
in punctul ![]() . Ori, in acest caz avem
. Ori, in acest caz avem 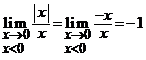 si
si 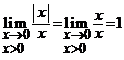 , deci limita acestui raport nu exista in
, deci limita acestui raport nu exista in ![]() si atunci,
functia modul nu este derivabila in origine.
si atunci,
functia modul nu este derivabila in origine.
33.
Definitie. Daca ![]() este punct de
acumulare pentru
este punct de
acumulare pentru ![]() si exista
limita finita
si exista
limita finita
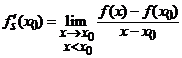 , cu
, cu ![]() , (4)
, (4)
atunci aceasta limita se
numeste derivata la stanga a
functiei ![]() in
in ![]() . Asemanator se defineste derivata la dreapta a functiei
. Asemanator se defineste derivata la dreapta a functiei ![]() in
in ![]() , notata cu
, notata cu ![]() .
.
Daca ![]() , atunci derivabilitatea lui
, atunci derivabilitatea lui ![]() in punctul
in punctul ![]() (respectiv in
(respectiv in ![]() ) revine la faptul ca functia
) revine la faptul ca functia ![]() este derivabila
la dreapta lui
este derivabila
la dreapta lui ![]() (respectiv la stanga
lui
(respectiv la stanga
lui ![]() ).
).
3 Propozitie. Fie ![]() ,
, ![]() o multime
deschisa si
o multime
deschisa si ![]() . Functia
. Functia ![]() este derivabila
in punctul
este derivabila
in punctul ![]() daca si
numai daca derivatele laterale
daca si
numai daca derivatele laterale ![]() si
si ![]() exista, sunt
finite si egale intre ele si atunci putem scrie
exista, sunt
finite si egale intre ele si atunci putem scrie
![]() .
.
Demonstratie. "![]() ". Presupunem ca
". Presupunem ca ![]() este derivabila
in
este derivabila
in ![]() . Atunci exista finita limita (5.1) si,
evident, exista
. Atunci exista finita limita (5.1) si,
evident, exista 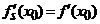 si
si ![]() , deci
, deci ![]() .
.
"![]() ". Presupunem ca exista si sunt egale
derivatele laterale ale
". Presupunem ca exista si sunt egale
derivatele laterale ale ![]() lui in
lui in ![]() . Vom nota cu
. Vom nota cu ![]() valoarea comuna a
acestor derivate,
valoarea comuna a
acestor derivate, ![]() . Aratam ca
. Aratam ca
![]() . (*)
. (*)
Fie ![]() , o vecinatate oarecare a lui
, o vecinatate oarecare a lui ![]() . Atunci exista vecinatatile
. Atunci exista vecinatatile ![]() si
si ![]() ale lui
ale lui ![]() a.i. pentru orice
a.i. pentru orice ![]() si
si ![]() sa avem
sa avem ![]() si pentru orice
si pentru orice ![]() cu
cu ![]() sa avem
sa avem ![]() . Consideram vecinatatea
. Consideram vecinatatea ![]() . Atunci pentru orice
. Atunci pentru orice ![]() vom avea fie
vom avea fie ![]() , deci
, deci ![]() , fie
, fie ![]() si deci
si deci ![]() . Aceste afirmatii arata ca se verifica
definitia limitei cu vecinatati si, in
consecinta, relatia (*) este verificata.
. Aceste afirmatii arata ca se verifica
definitia limitei cu vecinatati si, in
consecinta, relatia (*) este verificata.
35.
Definitie. Fie ![]() un interval deschis
si functia
un interval deschis
si functia ![]() . Functia
. Functia ![]() se numeste diferentiabila in punctul
se numeste diferentiabila in punctul ![]() daca si
numai daca exista numarul real
daca si
numai daca exista numarul real ![]() si o functie
si o functie
![]() ,
, ![]() continua in
continua in ![]() , cu
, cu ![]() a.i. sa aiba
loc relatia
a.i. sa aiba
loc relatia
![]() . (5)
. (5)
Numarul ![]() daca exista
este unic determinat si avem
daca exista
este unic determinat si avem ![]() (se citeste,
(se citeste, ![]() este derivata lui
este derivata lui ![]() in punctul
in punctul ![]() ), iar partea lineara
), iar partea lineara ![]() se numeste diferentiala lui
se numeste diferentiala lui ![]() in
in ![]() si uneori se
noteaza prin
si uneori se
noteaza prin
![]() . (6)
. (6)
sau, daca se noteaza ![]() , atunci se obtine notatia uzuala
, atunci se obtine notatia uzuala
![]() . (7)
. (7)
36.
Lema. Fie ![]() ,
, ![]() interval deschis si
interval deschis si
![]() , si fie functia
, si fie functia ![]() . Afirmatiile urmatoare sunt echivalente:
. Afirmatiile urmatoare sunt echivalente:
Functia ![]() este diferentiabila in
este diferentiabila in ![]() .
.
Exista o aplicatie lineara ![]() si o functie
si o functie
![]() ,
, ![]() continua in
continua in ![]() , cu
, cu ![]() , a.i. sa aiba loc relatia
, a.i. sa aiba loc relatia
![]() . (8)
. (8)
Demonstratie. "![]() ". Deoarece
". Deoarece ![]() este
diferentiabila in punctul
este
diferentiabila in punctul ![]() , vom nota cu
, vom nota cu ![]() si
si
definim functia
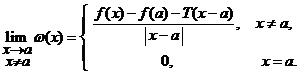 . (9)
. (9)
Este evident ca ![]() este continua in
este continua in ![]() si
si ![]() .
.
"![]() ". trivial.
". trivial.
37. Observatie. Egalitatea (8) poate fi scrisa sub urmatoarea forma
![]() . (10)
. (10)
Intr-adevar, din definitia
functiei ![]() deducem ca in
vecinatatea
deducem ca in
vecinatatea ![]() avem
avem
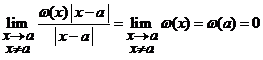 .
.
38.
Definitie. Fie ![]() ,
, ![]() multime
deschisa. Functia
multime
deschisa. Functia ![]() se numeste diferentiabila pe
se numeste diferentiabila pe ![]() daca este
diferentiabila in orice punct
daca este
diferentiabila in orice punct ![]() si avem
si avem ![]() definita prin
definita prin ![]() si se
citeste "derivata lui
si se
citeste "derivata lui ![]() in punctul
in punctul ![]() ". Deci
". Deci ![]() ,
, ![]() , fixat.
, fixat.
Atunci, folosind notatia uzuala, scriem
![]() . (11)
. (11)
Spunem ca functia ![]() este de clasa
este de clasa ![]() pe
pe ![]() si scriem
si scriem ![]() daca si
numai daca
daca si
numai daca ![]() este
diferentiabila (derivabila) in orice punct din
este
diferentiabila (derivabila) in orice punct din ![]() si derivata
si derivata ![]() continua pe
continua pe ![]() .
.
39. Observatie.
Daca ![]() este
diferentiabila pe
este
diferentiabila pe ![]() , atunci
, atunci ![]() ia valori in
ia valori in ![]() .
.
Deci ![]() si deoarece
si deoarece ![]() se identifica
izometric cu
se identifica
izometric cu ![]() , atunci putem considera pe
, atunci putem considera pe ![]() ca o functie
definita astfel
ca o functie
definita astfel ![]() .
.
40. Teorema (Operatii cu functii derivabile).
Fie ![]() , multime deschisa,
, multime deschisa, ![]() si
si ![]() .
.
(1). Daca ![]() si
si ![]() sunt
diferentiabile in
sunt
diferentiabile in ![]() atunci functia
atunci functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem ![]() .
.
(2). Daca ![]() este
diferentiabila in
este
diferentiabila in ![]() si
si ![]() atunci functia
atunci functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem ![]() .
.
(3). Daca ![]() , deci
, deci ![]() este functie
lineara atunci
este functie
lineara atunci ![]() diferentiabila in orice punct
diferentiabila in orice punct ![]() si avem
si avem ![]() .
.
(4). Daca ![]() si
si ![]() sunt
diferentiabile in
sunt
diferentiabile in ![]() atunci functia
atunci functia ![]() este
diferentiabila in
este
diferentiabila in ![]() si avem
si avem ![]() .
.
Demonstratie. Vom observa ca proprietatile
(1) si (2) arata ca derivata este un operator (o aplicatie
lineara) linear, adica ![]() si
si ![]() .
.
(1). Scriem
ca ![]() sunt functii
diferentiabile in
sunt functii
diferentiabile in ![]() : exista aplicatiile lineare si continue
: exista aplicatiile lineare si continue ![]() si functiile
si functiile
![]() continue in
continue in ![]() :,
:, ![]() a.i.
a.i.
![]() unde
unde ![]() .
.
![]() unde
unde ![]() .
.
Adunand aceste relatii si folosind
notatiile ![]() ,
, ![]() si
si ![]() , deducem ca functia
, deducem ca functia ![]() este
diferentiabila in
este
diferentiabila in ![]() .
.
(2). Din faptul ca ![]() este functie
diferentiabila in
este functie
diferentiabila in ![]() rezulta
existenta aplicatiei lineare si continue
rezulta
existenta aplicatiei lineare si continue ![]() si a
functiei
si a
functiei ![]() continua in
continua in ![]() ,
, ![]() a.i.
a.i.
![]() unde
unde ![]() .
.
Inmultind aceasta relatie cu ![]() , deducem ca
, deducem ca ![]() este
diferentiabila in
este
diferentiabila in ![]() , si are derivata
, si are derivata ![]() .
.
(3). Din faptul ca ![]() este aplicatie
lineara putem scrie
este aplicatie
lineara putem scrie
![]()
si luand ![]() si
si ![]() , rezulta afirmatia din enunt.
, rezulta afirmatia din enunt.
(4). Datorita ipotezei putem scrie
![]() si
si![]() .
.
Inmultind prima relatie cu ![]() si pe cea de a
doua cu
si pe cea de a
doua cu ![]() si apoi
adunam aceste relatii, obtinem
si apoi
adunam aceste relatii, obtinem
![]() ,
,
unde ![]() si
si ![]() . Relatia obtinuta arata ca
. Relatia obtinuta arata ca ![]() este
diferentiabila in
este
diferentiabila in ![]() .
.
Observatie.
Orice functie ![]() diferentiabila in
diferentiabila in ![]() este continua in
este continua in ![]() .
.
41.
Definitie. Fie ![]() ,
, ![]() multime
deschisa,
multime
deschisa, ![]() si
si ![]() . Functia
. Functia ![]() este de doua ori
diferentiabila in
este de doua ori
diferentiabila in ![]() daca:
daca:
(i). exista o vecinatate ![]() ,
, ![]() , a.i.
, a.i. ![]() este
diferentiabila pe
este
diferentiabila pe ![]() ;
;
(ii).
functia ![]() este
diferentiabila in
este
diferentiabila in ![]() .
.
In aceste conditii se
noteaza ![]() .
.
42.Observatie.
Functia ![]() este de doua ori
diferentiabila pe
este de doua ori
diferentiabila pe ![]() daca este de
doua ori diferentiabila in orice punct din
daca este de
doua ori diferentiabila in orice punct din ![]() ;
;
Functia ![]() este de clasa
este de clasa ![]() daca si
numai daca este de doua ori diferentiabila pe
daca si
numai daca este de doua ori diferentiabila pe ![]() si derivata
si derivata ![]() este continua pe
este continua pe ![]() .
.
Generalizarea acestor
definitii se poate face pentru orice intreg ![]() si derivata
si derivata ![]() .
.
Exercitiul
1. (Derivata functiei
compuse). Fie ![]() intervale deschise,
functia
intervale deschise,
functia ![]() , diferentiabila in
, diferentiabila in ![]() , functia
, functia ![]() diferentiabila in
diferentiabila in ![]() . Atunci functia compusa
. Atunci functia compusa ![]() este
diferentiabila in
este
diferentiabila in ![]() si are loc
relatia
si are loc
relatia
![]()
Exercitiul
2. (Derivata functiei
inverse). Fie ![]() intervale deschise
si functia
intervale deschise
si functia ![]() , continua si bijectiva. Daca
, continua si bijectiva. Daca ![]() este
diferentiabila in
este
diferentiabila in ![]() si
si ![]() atunci functia
inversa
atunci functia
inversa ![]() este
diferentiabila in
este
diferentiabila in ![]() si are loc
relatia
si are loc
relatia
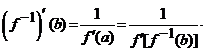
Exercitiu
3. Daca ![]() si sunt
derivabile in punctul
si sunt
derivabile in punctul ![]() (sau pe
(sau pe ![]() ) atunci functia
) atunci functia ![]() , daca
, daca ![]() este derivabila
in
este derivabila
in ![]() (sau pe
(sau pe ![]() ) si avem
) si avem
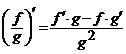 .
.
Daca ![]() sunt derivabile de
sunt derivabile de ![]() ori in
ori in ![]() (sau pe
(sau pe ![]() ) atunci
) atunci ![]() este derivabila
de
este derivabila
de ![]() ori in
ori in ![]() (sau pe
(sau pe ![]() ) si are loc formula
lui Leibniz
) si are loc formula
lui Leibniz
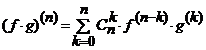 . (5.12)
. (5.12)
Exercitiul
Fie functiile ![]() si
si ![]() diferentiabile,
astfel incat are sens functia
diferentiabile,
astfel incat are sens functia ![]() care este
diferentiabila (vom scrie,
care este
diferentiabila (vom scrie, ![]() ). Atunci are loc relatia
). Atunci are loc relatia
![]() .
.
Exercitiul
5. Fie functia ![]() ,
, ![]() . Sa se arate ca
. Sa se arate ca ![]() este
diferentiabila in orice punct
este
diferentiabila in orice punct ![]() si
si ![]() .
.
R. Potrivit relatiei (5), putem scrie
(pentru ![]() ),
), ![]() .
.
Atunci, definim functia
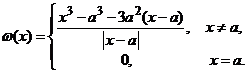
Se verifica usor ca ![]() este continua pe
este continua pe ![]() si
si ![]() . Asadar,
. Asadar, ![]() este
diferentiabila in
este
diferentiabila in ![]() .
.
Exercitiul
6. Aratati ca
functia ![]() ,
, ![]() nu este
diferentiabila in punctul
nu este
diferentiabila in punctul ![]() .
.
R. Presupunem ca ![]() ar fi
diferentiabila in
ar fi
diferentiabila in ![]() . Atunci exista unic numarul
. Atunci exista unic numarul ![]() si functia
si functia ![]() ,
, ![]() continua in
continua in ![]() , cu
, cu ![]() a.i.
a.i.
![]() .
.
Asadar, daca ![]() , din aceasta relatie, deducem urmatoarea
expresie pentru functia
, din aceasta relatie, deducem urmatoarea
expresie pentru functia ![]() :
:
![]() ,
,![]() .
.
Deoarece ![]() , atunci functia
, atunci functia ![]() , daca exista, are expresia
, daca exista, are expresia
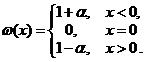
Din continuitatea lui ![]() deducem ca
deducem ca ![]() , ceea ce arata ca
, ceea ce arata ca ![]() ramane
nedeterminat si, in
consecinta,
ramane
nedeterminat si, in
consecinta, ![]() nu este
diferentiabila in origine.
nu este
diferentiabila in origine.
Exercitiul 7. Exista functii care sunt
derivabile intr-un punct ![]() fara ca
derivata sa
fara ca
derivata sa ![]() sa fie
continua in punctul
sa fie
continua in punctul ![]() . De exemplu, functia
. De exemplu, functia 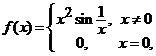 este continua pe
este continua pe ![]() , deci si in
, deci si in ![]() . Derivata
. Derivata ![]() exista si
este egala cu zero, insa functia derivata
exista si
este egala cu zero, insa functia derivata ![]() nu este nici
macar definita in origine.
nu este nici
macar definita in origine.
|
Politica de confidentialitate |
| Copyright ©
2026 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |