Au forma generala
![]() , (5.1)
, (5.1)
unde
![]() sunt functii continue
pe
sunt functii continue
pe ![]() , care verifica conditiile
, care verifica conditiile ![]() ,
, ![]()
![]() ,
,![]() fiind un interval al axei reale.
fiind un interval al axei reale.
Acest tip de ecuatii nu
poate fi rezolvat prin cuadraturi (adica, solutiile lor nu pot fi
exprimate cu ajutorul primitivelor de functii continue; de exemplu, ecuatia
Riccati ![]() , nu este integrabila prin cuadraturi[2]),
insa pot fi puse in evidenta cateva proprietati
remarcabile ale acestor ecuatii, care in unele situatii pot conduce
la obtinerea solutiei prin cuadraturi.
, nu este integrabila prin cuadraturi[2]),
insa pot fi puse in evidenta cateva proprietati
remarcabile ale acestor ecuatii, care in unele situatii pot conduce
la obtinerea solutiei prin cuadraturi.
i). Ecuatiile de tip Riccati nu au solutii singulare; toate solutiile ecuatiilor Riccati sunt solutii particulare.
ii). Daca se cunoaste o solutie particulara ![]() a ecuatiei
Riccati, atunci este posibila integrarea prin cuadraturi.
a ecuatiei
Riccati, atunci este posibila integrarea prin cuadraturi.
Intr-adevar, fie ![]() o solutie
particulara cunoscuta a ecuatiei Riccati si functia
o solutie
particulara cunoscuta a ecuatiei Riccati si functia ![]() o alta
solutie a acestei ecuatii, atunci functia
o alta
solutie a acestei ecuatii, atunci functia ![]() verifica o
ecuatie de tip Bernoulli cu
verifica o
ecuatie de tip Bernoulli cu ![]() . Avem
. Avem
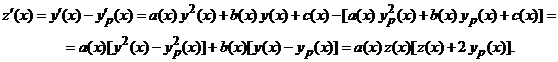
Deci ![]() verifica
ecuatia de tip Bernoulli
verifica
ecuatia de tip Bernoulli
![]() . (5.2)
. (5.2)
Aplicand algoritmul de rezolvare a
ecuatiei de tip Bernoulli, deducem ca functia ![]() poate fi determinata
cu ajutorul ecuatiei lineare si neomogene asociate pe care o
verifica functia
poate fi determinata
cu ajutorul ecuatiei lineare si neomogene asociate pe care o
verifica functia ![]() si deci, solutia
si deci, solutia
![]() a ecuatiei Riccati, inca necunoscuta, se poate
determina.
a ecuatiei Riccati, inca necunoscuta, se poate
determina.
Prin urmare, daca se face schimbarea de
functie ![]() , se obtine o ecuatie lineara in
, se obtine o ecuatie lineara in ![]() . Asadar, daca se cunoaste o solutie
particulara a ecuatiei de tip Riccati (5.1), toate celelalte
solutii pot fi determinate prin cuadraturi. S-a stabilit urmatorul
rezultat: functia
. Asadar, daca se cunoaste o solutie
particulara a ecuatiei de tip Riccati (5.1), toate celelalte
solutii pot fi determinate prin cuadraturi. S-a stabilit urmatorul
rezultat: functia ![]() este solutie a
ecuatiei de Riccati (5.1) daca si numai daca
functia
este solutie a
ecuatiei de Riccati (5.1) daca si numai daca
functia ![]() este solutie a
ecuatiei de tip Bernoulli (5.2).
este solutie a
ecuatiei de tip Bernoulli (5.2).
In general, nu se cunoaste o metoda pentru determinarea unei solutii particulare a ecuatiei Riccati. Cand coeficientii ecuatiei au forme particulare, putem incerca sa gasim solutii particulare de forme apropiate; de exemplu, daca coeficientii ecuatiei sunt polinoame, cautam solutia sub forma de putere, un polinom sau o fractie. Solutiile particulare pot fi obtinute, de exemplu, cu metoda seriilor Taylor (vezi Kamke).
iii). Daca pentru ecuatia Riccati (5.1)
cunoastem doua solutii particulare ![]() si
si ![]() , atunci pentru ecuatia Bernoulli asociata
cunoastem solutia particulara
, atunci pentru ecuatia Bernoulli asociata
cunoastem solutia particulara ![]() . Deci, se cunoaste o solutie particulara a
ecuatiei lineare asociate ecuatiei Bernoulli (
. Deci, se cunoaste o solutie particulara a
ecuatiei lineare asociate ecuatiei Bernoulli (![]() si cu schimbarea de functie
si cu schimbarea de functie ![]()
![]() ) si atunci, printr-o cuadratura se determina
toate solutiile ecuatiei lineare (se rezolva ecuatia
lineara omogena asociata).
) si atunci, printr-o cuadratura se determina
toate solutiile ecuatiei lineare (se rezolva ecuatia
lineara omogena asociata).
Asadar, daca ![]() si
si ![]() sunt solutii
particulare pentru ecuatia Riccati (5.1), atunci cu schimbarea de
functie
sunt solutii
particulare pentru ecuatia Riccati (5.1), atunci cu schimbarea de
functie
![]() , (5.3)
, (5.3)
deducem
ca functia ![]() este solutie a
ecuatiei cu variabile separabile
este solutie a
ecuatiei cu variabile separabile
![]() (5.4)
(5.4)
iv). Daca in ecuatia Riccati (5.1) facem o transformare omografica
![]() , cu
, cu ![]() , (5.5)
, (5.5)
atunci
functia ![]() , definita de (5.5), verifica tot o ecuatie de tip
Riccati.
, definita de (5.5), verifica tot o ecuatie de tip
Riccati.
Intr-adevar, se stie ca solutiile ecuatiilor
diferentiale lineare au forma ![]() , unde
, unde ![]() este o constanta,
este o constanta,
![]() este o solutie a
ecuatiei omogene asociate si
este o solutie a
ecuatiei omogene asociate si ![]() este o solutie
particulara a ecuatiei neomogene. Deci, solutiile ecuatiei
Bernoulli in
este o solutie
particulara a ecuatiei neomogene. Deci, solutiile ecuatiei
Bernoulli in ![]() , corespunzatoare, au forma
, corespunzatoare, au forma ![]() , si atunci solutiile ecuatiei Riccati au
forma
, si atunci solutiile ecuatiei Riccati au
forma
![]() , (5.6)
, (5.6)
unde
![]() este o solutie
particulara a ecuatiei Riccati. Relatia (5.6) poate fi
scrisa sub forma
este o solutie
particulara a ecuatiei Riccati. Relatia (5.6) poate fi
scrisa sub forma
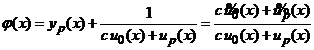 . (5.7)
. (5.7)
Relatia (5.7) arata ca solutia generala a ecuatiei Riccati (5.1) este o functie omografica de constanta de integrare.
v) Daca se cunosc trei solutii
particulare diferite, definite pe acelasi interval I, ale ecuatiei Riccati, atunci din proprietatea iv) rezulta ca raportul
anarmonic al acestor solutii este invariant si atunci fie ![]() cea de a patra
solutie. Daca scriem ca raportul anarmonic al solutiilor
cea de a patra
solutie. Daca scriem ca raportul anarmonic al solutiilor ![]() este constant, avem
este constant, avem
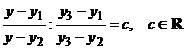 ,
,
Atunci din relatia (5.8) deducem expresia solutiei generale a ecuatiei Riccati.
Observatie. Inainte
de a fi utilizate in calcule vom avea grija sa verificam ca
![]() sunt solutii
particulareale ecuatiei Riccati.
sunt solutii
particulareale ecuatiei Riccati.
Exercitii
) Determinati solutiile urmatoarelor ecuatii Riccati daca se cunoaste o solutie particulara:
i ![]() .
.
ii ![]() .
.
iii) ![]() ; Se va cauta o solutie particulara de
forma
; Se va cauta o solutie particulara de
forma ![]() (dupa
determinarea constantelor a si b avem
(dupa
determinarea constantelor a si b avem ![]() ).
).
iv) ![]() .
.
. Determinati solutiile ecuatiilor Riccati, daca se cunosc doua solutii particulare:
i) ![]() ; Se cauta o
solutie particulara de forma
; Se cauta o
solutie particulara de forma ![]() ,
, ![]() . (Prin inlocuirea in ecuatia data avem
. (Prin inlocuirea in ecuatia data avem 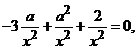 de unde obtinem
ecuatia
de unde obtinem
ecuatia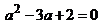 , cu radacinile
, cu radacinile
![]() sau
sau ![]() . Luand oricare din aceste valori obtinem o solutie
particulara). Asadar, avem doua solutii particulare
. Luand oricare din aceste valori obtinem o solutie
particulara). Asadar, avem doua solutii particulare ![]() si respectiv
si respectiv ![]() .
.
Ecuatia are forma ![]() ; unde
; unde ![]() ,
, ![]() sunt solutii particulare.
sunt solutii particulare.
Daca punem ![]() si deducem
ca z verifica ecuatia
cu variabile separabile
si deducem
ca z verifica ecuatia
cu variabile separabile ![]() ,
, ![]() . Atunci
. Atunci
![]() ;
; ![]() T solutia este
T solutia este ![]() .
.
. Determinati solutia ecuatiei
![]() daca se cunosc
trei solutii particulare:
daca se cunosc
trei solutii particulare: ![]() .
.
Riccati
Giordano (1709-1790), fizician italian, doctor in drept, s-a ocupat de
arhitectura. Are numeroase cercetari in domeniul acusticii si
asupra oscilatiilor firelor elastice (Delle corde ovvero fibre elastiche,
In 1694,
J. Bernoulli gaseste prima functie Bessel integrand ecuatia
de tip Riccati ![]() . In 1841, J. Liouville a demonstrat ca exista
ecuatii de tip Riccati care nu sunt integrabile prin cuadraturi; de
exemplu, ecuatiile de tip Riccati de forma
. In 1841, J. Liouville a demonstrat ca exista
ecuatii de tip Riccati care nu sunt integrabile prin cuadraturi; de
exemplu, ecuatiile de tip Riccati de forma ![]() unde
unde ![]() , sunt integrabile prin cuadraturi daca si numai
daca
, sunt integrabile prin cuadraturi daca si numai
daca ![]() sau exista
sau exista ![]() astfel incat
astfel incat ![]() .
.
|
Politica de confidentialitate |
| Copyright ©
2025 - Toate drepturile rezervate. Toate documentele au caracter informativ cu scop educational. |
Personaje din literatura |
| Baltagul – caracterizarea personajelor |
| Caracterizare Alexandru Lapusneanul |
| Caracterizarea lui Gavilescu |
| Caracterizarea personajelor negative din basmul |
Tehnica si mecanica |
| Cuplaje - definitii. notatii. exemple. repere istorice. |
| Actionare macara |
| Reprezentarea si cotarea filetelor |
Geografie |
| Turismul pe terra |
| Vulcanii Și mediul |
| Padurile pe terra si industrializarea lemnului |
| Termeni si conditii |
| Contact |
| Creeaza si tu |